Στερεό του Αρχιμήδη

Στερεό του Αρχιμήδη (ή Αρχιμήδειο στερεό) είναι ένα κυρτό ημικανονικό πολύεδρο, οι έδρες του οποίου είναι κανονικά πολύγωνα, αλλά όχι του ίδιου τύπου, αντίθετα με ό,τι συμβαίνει στα Πλατωνικά στερεά.[1]
Τα κανονικά πολύγωνα, που αποτελούν τις έδρες, έχουν όλα ίσες τις πλευρές τους, δηλαδή οι ακμές του πολυέδρου είναι όλες ίσες. Οι έδρες ενώνονται με τον ίδιο ακριβώς τρόπο σε κάθε κορυφή του πολυέδρου, διαμορφώνοντας ίσες πολυεδρικές γωνίες. Για παράδειγμα, στο διπλανό ρομβοεικοσιδωδεκάεδρο η διαμόρφωση κορυφής είναι (3.4.5.4), δηλαδή οι πολυγωνικές έδρες που φτιάχνουν την κάθε κορυφή του πολυέδρου είναι: τρίγωνο-τετράγωνο-πεντάγωνο-τετράγωνο (πάντα με αυτήν ακριβώς τη σειρά).
Τα στερεά του Αρχιμήδη είναι 13 και έχουν ως έδρες δύο ή τρία διαφορετικά κανονικά πολύγωνα. Όλα μπορούν να προκύψουν από τα Πλατωνικά στερεά μέσω κατάλληλων μετασχηματισμών, όπως αποκοπή των κορυφών ή των ακμών κ.ά.[1]
Ονομάστηκαν έτσι, επειδή τα ανακάλυψε ο Αρχιμήδης, ο οποίος τα διαπραγματευόταν στο έργο του «Περί 13 ημικανονικών πολυέδρων», που δεν έχει διασωθεί.[1]
Χαρακτηριστικά
[Επεξεργασία | επεξεργασία κώδικα]| Πολύεδρο (Διαμόρφωση κορυφής) |
Εικόνα | Ανάπτυγμα | Έδρες | Ακμές | Κορυφές | Ομάδα συμμετρίας | |
|---|---|---|---|---|---|---|---|
| Κόλουρο τετράεδρο (3.6.6) |
 (κινούμενο μοντέλο) |
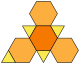
|
8 | 4 τρίγωνα 4 εξάγωνα |
18 | 12 | Td |
| Κυβοκτάεδρο (3.4.3.4) |
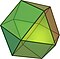 (κινούμενο μοντέλο) |
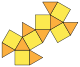
|
14 | 8 τρίγωνα 6 τετράγωνα |
24 | 12 | Oh |
| Κόλουρος κύβος ή κόλουρο εξάεδρο (3.8.8) |
 (κινούμενο μοντέλο) |
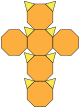
|
14 | 8 τρίγωνα 6 οκτάγωνα |
36 | 24 | Oh |
| Κόλουρο οκτάεδρο (4.6.6) |
 |

|
14 | 6 τετράγωνα 8 εξάγωνα |
36 | 24 | Oh |
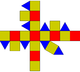
| Ρομβοκυβοκτάεδρο ή μικρό ρομβοκυβοκτάεδρο (3.4.4.4 ) |
 (κινούμενο μοντέλο) |
|
26 | 8 τρίγωνα 18 τετράγωνα |
48 | 24 | Oh |
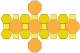
| Κόλουρο κυβοκτάεδρο ή μεγάλο ρομβοκυβοκτάεδρο (4.6.8) |
 (κινούμενο μοντέλο) |
|
26 | 12 τετράγωνα 8 εξάγωνα 6 οκτάγωνα |
72 | 48 | Oh |
| Πεπλατυσμένος κύβος ή πεπλατυσμένο εξάεδρο ή πεπλατυσμένο κυβοκτάεδρο (2 εναντιόμορφα) (3.3.3.3.4) |
 (κινούμενο μοντέλο)  (κινούμενο μοντέλο) |

|
38 | 32 τρίγωνα 6 τετράγωνα |
60 | 24 | O |
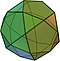
| Εικοσιδωδεκάεδρο (3.5.3.5) |
 (κινούμενο μοντέλο) |

|
32 | 20 τρίγωνα 12 πεντάγωνα |
60 | 30 | Ih |
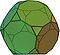
| Κόλουρο δωδεκάεδρο (3.10.10) |
 (κινούμενο μοντέλο) |

|
32 | 20 τρίγωνα 12 δεκάγωνα |
90 | 60 | Ih |
| Κόλουρο εικοσάεδρο (5.6.6 ) |
 (κινούμενο μοντέλο) |

|
32 | 12 πεντάγωνα 20 εξάγωνα |
90 | 60 | Ih |
| Ρομβοεικοσιδωδεκάεδρο ή μικρό ρομβοεικοσιδωδεκάεδρο (3.4.5.4) |
 (κινούμενο μοντέλο) |

|
62 | 20 τρίγωνα 30 τετράγωνα 12 πεντάγωνα |
120 | 60 | Ih |
| Κόλουρο εικοσιδωδεκάεδρο ή μεγάλο ρομβοεικοσιδωδεκάεδρο (4.6.10) |
 (κινούμενο μοντέλο) |

|
62 | 30 τετράγωνα 20 εξάγωνα 12 δεκάγωνα |
180 | 120 | Ih |
| Πεπλατυσμένο δωδεκάεδρο ή πεπλατυσμένο εικοσιδωδεκάεδρο (2 εναντιόμορφα) (3.3.3.3.5) |
 (κινούμενο μοντέλο)  (κινούμενο μοντέλο) |

|
92 | 80 τρίγωνα 12 πεντάγωνα |
150 | 60 | I |
Ο πεπλατυσμένος κύβος και το πεπλατυσμένο δωδεκάεδρο είναι χειρικά, δηλαδή εμφανίζονται σε δύο αντικατοπτρικές μορφές, τα εναντιόμορφα (δεξιόστροφο και αριστερόστροφο).
Για το συνολικό πλήθος των εδρών E, των κορυφών K και των ακμών A ισχύει ο τύπος του Euler:
Κάθε στερεό του Αρχιμήδη είναι εγγράψιμο σε σφαίρα, δηλαδή όλες οι κορυφές ισαπέχουν από το κέντρο του πολυέδρου. Επίσης, όλες οι ακμές του πολυέδρου ισαπέχουν από το κέντρο του. Όσον αφορά τις έδρες, ισαπέχουν από το κέντρο μόνο όσες είναι του ίδιου τύπου.[1]
Τα δυϊκά (συζυγή) πολύεδρα των στερεών του Αρχιμήδη είναι τα Καταλανικά στερεά.[1]
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]Πηγές
[Επεξεργασία | επεξεργασία κώδικα]- Σωτήρης Γκουντουβάς, Γεωμετρικές Διαδρομές, Γ' έκδοση, Αθήνα 2021.
- Κέντρο Έρευνας Επιστήμης και Εκπαίδευσης, "Ευκλείδη Στοιχεία", τόμος 3, κεφ. 3 (Αθήνα 2001, ISBN 960-86879-2-6)
- ΟΕΔΒ, Ευκλείδεια Γεωμετρία Α' - Β' Γενικού Λυκείου, κεφ. 13 (συμπιεσμένο αρχείο)
- Weisstein, Eric W., Archimedean Solid (Αγγλικά)

