Πεπλατυσμένος κύβος

Πεπλατυσμένος κύβος
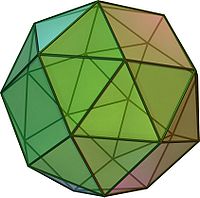(κινούμενο μοντέλο)
Τύπος	Στερεό του Αρχιμήδη
Έδρες	38 32 τρίγωνα 6 τετράγωνα
Ακμές	60
Κορυφές	24
Διαμόρφωση κορυφής	(3.3.3.3.4)
Ομάδα συμμετρίας	οκταεδρική (O)
Δυϊκό	Πενταγωνικό εικοσιτετράεδρο
Ανάπτυγμα

Στη στερεομετρία, ο πεπλατυσμένος κύβος (ή πεπλατυσμένο εξάεδρο ή πεπλατυσμένο κυβοκτάεδρο) είναι ένα κυρτό ημικανονικό πολύεδρο, που ανήκει στα στερεά του Αρχιμήδη. Διαθέτει 38 έδρες: 32 ισόπλευρα τρίγωνα και 6 τετράγωνα. Έχει 24 κορυφές και 60 ακμές.

Το στερεό απαντάται σε δύο μορφές, που είναι μεταξύ τους αντικατοπτρικές, οι οποίες λέγονται εναντιόμορφα, το ένα αριστερόστροφο και το άλλο δεξιόστροφο. Αυτό το φαινόμενο του εναντιομορφισμού παρουσιάζεται και σε ένα ακόμη στερεό του Αρχιμήδη, το πεπλατυσμένο δωδεκάεδρο.

Γεωμετρικά χαρακτηριστικά πεπλατυσμένου κύβου

Αν θεωρήσουμε $\alpha \,\!$ το μήκος της ακμής του στερεού, τότε ισχύουν τα εξής:

Ακτίνα περιγεγραμμένης σφαίρας (απόσταση κορυφών από το κέντρο)	$R={\sqrt {\frac {3-t}{4(2-t)}}}\alpha \approx 1,344\alpha$
Απόσταση ακμών από το κέντρο	$\rho ={\sqrt {\frac {1}{4(2-t)}}}\alpha \approx 1,247\alpha$
Απόσταση τριγωνικών εδρών από το κέντρο	$r_{3}={\sqrt {\frac {t+1}{12(2-t)}}}\alpha \approx 1,213\alpha$
Απόσταση τετραγωνικών εδρών από το κέντρο	$r_{4}={\sqrt {\frac {1-t}{4(t-2)}}}\alpha \approx 1,143\alpha$
Συνολική επιφάνεια	$S=\left(6+8{\sqrt {3}}\right)\alpha ^{2}\approx 19,856\alpha ^{2}$
Όγκος	$V={\sqrt {\frac {613t+203}{9(35t-62)}}}\alpha ^{3}\approx 7,889\alpha ^{3}$

όπου $t={\frac {1}{3}}\left(1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}\right)\approx 1,83929$ η σταθερά tribonacci.

Κατασκευαστικά, ο πεπλατυσμένος κύβος μπορεί να προέλθει από τον κύβο, εάν απομακρύνουμε προς τα έξω (σε σχέση με το κέντρο του) όλες τις έδρες του κατά ορισμένη απόσταση και τις περιστρέψουμε ως προς το κέντρο τους (όλες αριστερόστροφα ή όλες δεξιόστροφα), έτσι ώστε τα κενά που δημιουργούνται να μπορούν να καλυφθούν από ισόπλευρα τρίγωνα.

Ένας άλλος τρόπος κατασκευής του πεπλατυσμένου κύβου είναι να λάβουμε ένα κόλουρο κυβοκτάεδρο και να του απαλείψουμε τις μισές κορυφές (ομοιόμορφα κατανεμημένα, αριστερόστροφα ή δεξιόστροφα, όπως φαίνεται στο σχήμα). Έτσι, τα 6 οκτάγωνα του αρχικού στερεού μετατρέπονται σε ισάριθμα τετράγωνα, τα 8 εξάγωνα μετατρέπονται σε ισάριθμα τρίγωνα, όλα τα τετράγωνα εκφυλίζονται σε ακμές, ενώ οι 24 κορυφές που απαλείφονται σχηματίζουν ισάριθμα τρίγωνα.

Κύβος

Πεπλατυσμένος κύβος

Πηγές - Παραπομπές

• Weisstein, Eric W., Snub Cube (Αγγλικά)