Πρώτος αριθμός

Στα μαθηματικά πρώτος αριθμός (ή απλά πρώτος) είναι ένας φυσικός αριθμός με την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του. Ένας φυσικός αριθμός, ο οποίος δεν είναι πρώτος αριθμός ονομάζεται σύνθετος αριθμός. Για παράδειγμα, ο αριθμός 5 είναι πρώτος, επειδή οι μόνοι τελειοι διαιρέτες του είναι το 1 και το 5, ενώ το 6 είναι σύνθετος επειδή έχει διαιρέτες του το 2 και 3 εκτός των 1 και 6. Το μηδέν και το ένα δεν θεωρούνται πρώτοι αριθμοί.

Η ακολουθία των 25 πρώτων αριθμών είναι η εξής

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, ...

Ο αριθμός 2 είναι ο μόνος άρτιος (ζυγός) πρώτος αριθμός. Όλοι οι άλλοι πρώτοι είναι περιττοί (μονοί).

Το θεμελιώδες θεώρημα της αριθμητικής καθορίζει το βασικό ρόλο των πρώτων αριθμών στη θεωρία αριθμών: κάθε ακέραιος αριθμός μεγαλύτερος του 1 μπορεί να γραφεί ως γινόμενο πρώτων κατά μοναδικό τρόπο, χωρίς να λαμβάνεται υπόψη η σειρά των παραγόντων. Η μοναδικότητα σε αυτό το θεώρημα προϋποθέτει την εξαίρεση του 1 ως πρώτου αριθμού επειδή ένας πρώτος μπορεί να περιέχει αυθαίρετα πολλές φορές το 1 σε κάθε γινόμενο, για παράδειγμα 3, 1 x 3, 1 x 1 x 3, κ.ο.κ. είναι όλοι παράγοντες του 3.

Μια απλή αλλά αργή μέθοδος για να επαληθευτεί αν ένας δοθείς αριθμός n είναι πρώτος είναι η λεγόμενη δοκιμαστική διαίρεση. Η δοκιμαστική διαίρεση συνίσταται στον έλεγχο αν ο n είναι πολλαπλάσιο κάποιου ακέραιου αριθμού μεταξύ του 2 και του √n. Οι αλγόριθμοι που είναι πολύ πιο αποτελεσματικοί από τη δοκιμαστική διαίρεση έχουν επινοηθεί για να ελέγχουμε αν μεγαλύτεροι αριθμοί είναι πρώτοι. Ιδιαίτερα γρήγορες μέθοδοι είναι διαθέσιμες για αριθμούς ειδικών μορφών, όπως είναι αριθμοί Μερσέν. Ο γνωστός πρώτος αριθμός από τον Δεκέμβριο του 2018 είναι ο M82589933 με 24.862.048 ψηφία.

Υπάρχουν άπειροι σε πλήθος πρώτοι αριθμοί, όπως απέδειξε ο Ευκλείδης περίπου στο 300 π.Χ. Δεν υπάρχει κανένας γνωστός τύπος ο οποίος να διαχωρίζει όλους τους πρώτους αριθμούς από τους σύνθετους. Ωστόσο, η κατανομή των πρώτων αριθμών, όπως λέμε τη στατιστική συμπεριφορά των πρώτων γενικά, μπορεί να μοντελοποιηθεί. Το πρώτο αποτέλεσμα προς αυτή την κατεύθυνση είναι το θεώρημα πρώτων αριθμών, το οποίο αποδείχτηκε στα τέλη του 19ου αιώνα, το οποίο λέει ότι η πιθανότητα ενός τυχαία επιλεγμένου αριθμού n να είναι πρώτος είναι αντιστρόφως ανάλογη του πλήθους των ψηφίων ή του λογαρίθμου του n.

Οι πρώτοι αριθμοί είναι ένα από τα αντικείμενα της θεωρίας αριθμών και είναι μια πολύ ενεργή ερευνητικά περιοχή των μαθηματικών. Πολλά ερωτήματα γύρω από τους πρώτους αριθμούς παραμένουν ανοιχτά, όπως η υπόθεση Ρίμαν, η εικασία του Γκόλντμπαχ, η οποία λέει ότι κάθε άρτιος ακέραιος μεγαλύτερος του 2 μπορεί να γραφεί ως άθροισμα δύο πρώτων και η εικασία των διδύμων πρώτων, η οποία λέει ότι υπάρχουν άπειρα σε πλήθος ζευγάρια πρώτων των οποίων η διαφορά είναι 2. Τέτοιες ερωτήσεις οδήγησαν στην ανάπτυξη διάφορων κλάδων της θεωρίας αριθμών, εστιάζοντας στην αναλυτική ή αλγεβρική πλευρά των αριθμών. Οι πρώτοι χρησιμοποιούνται σε πολλούς τομείς στην τεχνολογία πληροφοριών, όπως στην Κρυπτογράφηση Δημόσιου Κλειδιού, η οποία χρησιμοποιεί ιδιότητες, όπως τη δυσκολία να αναλύεις ένα μεγάλο αριθμό σε γινόμενο πρώτων αριθμών. Οι πρώτοι αριθμοί συμβάλλουν σε διάφορες γενικεύσεις σε άλλους μαθηματικούς τομείς, ιδίως στην άλγεβρα, όπως τα στοιχεία πρώτων και τα ιδανικά πρώτων.

Ορισμός και παραδείγματα

Ένας φυσικός αριθμός (όπως 1, 2, 3, 4, 5, κ.ο.κ.) ονομάζεται πρώτος ή πρώτος αριθμός αν έχει ακριβώς δύο θετικούς διαιρέτες, το 1 και τον εαυτό του. Οι φυσικοί αριθμοί μεγαλύτεροι της μονάδας που δεν είναι πρώτοι ονομάζονται σύνθετοι. Ο ορισμός των πρώτων αριθμών γενικεύεται και στους ακέραιους: ένας ακέραιος αριθμός p, διάφορος του μηδενός και των ±1, που έχει ως διαιρέτες μόνο τους ±1 και ±p, καλείται πρώτος. Οι αριθμοί π.χ. 2, 3, 5 είναι πρώτοι, όπως και οι -2, -3, -5.

Ο αριθμός 12 δεν είναι πρώτος, καθώς 12 αντικείμενα μπορούν να τοποθετηθούν σε 3 ισομεγέθεις στήλες με 4 αντικείμενα η καθεμία (μεταξύ άλλων τρόπων). 11 αντικείμενα δεν μπορούν να τοποθετηθούν σε αρκετές ισομεγέθεις στήλες με παραπάνω από ένα αντικείμενο σε καθεμία χωρίς να περισσεύουν κάποια παραπάνω αντικείμενα (υπόλοιπο). Επομένως, ο αριθμός 11 είναι πρώτος.

Μεταξύ των αριθμών 1 και 6, οι αριθμοί 2, 3 και 5 είναι πρώτοι, ενώ οι αριθμοί 1, 4 και 6 δεν είναι πρώτοι. Ο 1 εξαιρείται από τους πρώτους αριθμούς για τους λόγους που εξηγούνται παρακάτω. Ο 2 είναι πρώτος αριθμός, διότι οι μόνοι φυσικοί αριθμοί που τον διαιρούν είναι οι 1 και 2. Στη συνέχεια, ο 3 είναι πρώτος επίσης επειδή οι 1 και 3 διαιρούν τον 3 χωρίς υπόλοιπο, αλλά ο 3 διαιρείται από το 2 με υπόλοιπο 1. Έτσι, ο 3 είναι πρώτος. Ωστόσο, ο 4 είναι σύνθετος, αφού ο 2 είναι ένας άλλος αριθμός (εκτός των 1 και 4) που διαιρεί τον 4 χωρίς υπόλοιπο:

$4=2\cdot 2$.

Ο 5 είναι επίσης πρώτος, επειδή κανένας από τους αριθμούς 2, 3, 4 δε διαιρεί τον 5. Στη συνέχεια, ο 6 διαιρείται από τους 2 και 3, αφού

$6=2\cdot 3$.

Άρα, ο 6 δεν είναι πρώτος. Η εικόνα στα δεξιά απεικονίζει ότι ο 12 δεν είναι πρώτος: 12 = 3 · 4. Κανένας άρτιος αριθμός μεγαλύτερος του 2 δεν είναι πρώτος, επειδή εξ ορισμού κάθε τέτοιος αριθμός n έχει τουλάχιστον τρεις διαφορετικούς διαιρέτες, τους 1, 2 και n. Αυτό συνεπάγεται ότι ο n δεν είναι πρώτος. Επομένως, ο όρος περιττός πρώτος αναφέρεται σε κάθε πρώτο αριθμό μεγαλύτερο του 2. Ανάλογα, όλοι οι πρώτοι μεγαλύτεροι του 5, γραμμένοι στο σύνηθες δεκαδικό σύστημα, τελειώνουν σε 1, 3, 7 ή 9, αφού οι άρτιοι αριθμοί είναι πολλαπλάσια του 2 και οι αριθμοί που τελειώνουν σε 0 ή 5 είναι πολλαπλάσια του 5.

Αν ο n είναι ένας φυσικός αριθμός, τότε οι αριθμοί 1 και n τον διαιρούν χωρίς υπόλοιπο. Συνεπώς, η προϋπόθεση ένας αριθμός να είναι πρώτος μπορεί να επαναδιατυπωθεί ως εξής: ένας αριθμός είναι πρώτος αν είναι του 1 και αν κανείς από τους

$2,3,\ldots ,n-1$

δε διαιρεί τον n (χωρίς υπόλοιπο). Επιπλέον, ένας άλλος τρόπος να πούμε το ίδιο είναι: ένας αριθμός n > 1 είναι πρώτος αν δε μπορεί να γραφεί ως γινόμενο δύο ακεραίων α και b, όπου α και b είναι μεγαλύτεροι του 1:

$n=\alpha \cdot b$.

Με άλλα λόγια, ο n είναι πρώτος αν n αντικείμενα δεν μπορούν να διαιρεθούν σε μικρότερες ισομεγέθεις ομάδες με παραπάνω από ένα αντικείμενα.

Οι μικρότεροι 168 πρώτοι αριθμοί (όλοι οι πρώτοι αριθμοί μικρότεροι του 1000) είναι όπως παρακάτω με γαλανή επισήμανση κατά την διάταξη σπείρας Ούλαμ (με πράσινο χρώμα στο υπόβαθρο οι αριθμοί με μόνο 3 διαιρέτες, και με κόκκινο με μεγάλο αριθμό διαιρετών, περιλαμβάνονται και οι 13 πρώτοι αριθμοί από το 1000 έως το 1088):

1024	1023	1022	1021	1020	1019	1018	1017	1016	1015	1014	1013	1012	1011	1010	1009	1008	1007	1006	1005	1004	1003	1002	1001	1000	999	998	997	996	995	994	993	992
1025	900	899	898	897	896	895	894	893	892	891	890	889	888	887	886	885	884	883	882	881	880	879	878	877	876	875	874	873	872	871	870	991
1026	901	784	783	782	781	780	779	778	777	776	775	774	773	772	771	770	769	768	767	766	765	764	763	762	761	760	759	758	757	756	869	990
1027	902	785	676	675	674	673	672	671	670	669	668	667	666	665	664	663	662	661	660	659	658	657	656	655	654	653	652	651	650	755	868	989
1028	903	786	677	576	575	574	573	572	571	570	569	568	567	566	565	564	563	562	561	560	559	558	557	556	555	554	553	552	649	754	867	988
1029	904	787	678	577	484	483	482	481	480	479	478	477	476	475	474	473	472	471	470	469	468	467	466	465	464	463	462	551	648	753	866	987
1030	905	788	679	578	485	400	399	398	397	396	395	394	393	392	391	390	389	388	387	386	385	384	383	382	381	380	461	550	647	752	865	986
1031	906	789	680	579	486	401	324	323	322	321	320	319	318	317	316	315	314	313	312	311	310	309	308	307	306	379	460	549	646	751	864	985
1032	907	790	681	580	487	402	325	256	255	254	253	252	251	250	249	248	247	246	245	244	243	242	241	240	305	378	459	548	645	750	863	984
1033	908	791	682	581	488	403	326	257	196	195	194	193	192	191	190	189	188	187	186	185	184	183	182	239	304	377	458	547	644	749	862	983
1034	909	792	683	582	489	404	327	258	197	144	143	142	141	140	139	138	137	136	135	134	133	132	181	238	303	376	457	546	643	748	861	982
1035	910	793	684	583	490	405	328	259	198	145	100	99	98	97	96	95	94	93	92	91	90	131	180	237	302	375	456	545	642	747	860	981
1036	911	794	685	584	491	406	329	260	199	146	101	64	63	62	61	60	59	58	57	56	89	130	179	236	301	374	455	544	641	746	859	980
1037	912	795	686	585	492	407	330	261	200	147	102	65	36	35	34	33	32	31	30	55	88	129	178	235	300	373	454	543	640	745	858	979
1038	913	796	687	586	493	408	331	262	201	148	103	66	37	16	15	14	13	12	29	54	87	128	177	234	299	372	453	542	639	744	857	978
1039	914	797	688	587	494	409	332	263	202	149	104	67	38	17	4	3	2	11	28	53	86	127	176	233	298	371	452	541	638	743	856	977
1040	915	798	689	588	495	410	333	264	203	150	105	68	39	18	5	0	1	10	27	52	85	126	175	232	297	370	451	540	637	742	855	976
1041	916	799	690	589	496	411	334	265	204	151	106	69	40	19	6	7	8	9	26	51	84	125	174	231	296	369	450	539	636	741	854	975
1042	917	800	691	590	497	412	335	266	205	152	107	70	41	20	21	22	23	24	25	50	83	124	173	230	295	368	449	538	635	740	853	974
1043	918	801	692	591	498	413	336	267	206	153	108	71	42	43	44	45	46	47	48	49	82	123	172	229	294	367	448	537	634	739	852	973
1044	919	802	693	592	499	414	337	268	207	154	109	72	73	74	75	76	77	78	79	80	81	122	171	228	293	366	447	536	633	738	851	972
1045	920	803	694	593	500	415	338	269	208	155	110	111	112	113	114	115	116	117	118	119	120	121	170	227	292	365	446	535	632	737	850	971
1046	921	804	695	594	501	416	339	270	209	156	157	158	159	160	161	162	163	164	165	166	167	168	169	226	291	364	445	534	631	736	849	970
1047	922	805	696	595	502	417	340	271	210	211	212	213	214	215	216	217	218	219	220	221	222	223	224	225	290	363	444	533	630	735	848	969
1048	923	806	697	596	503	418	341	272	273	274	275	276	277	278	279	280	281	282	283	284	285	286	287	288	289	362	443	532	629	734	847	968
1049	924	807	698	597	504	419	342	343	344	345	346	347	348	349	350	351	352	353	354	355	356	357	358	359	360	361	442	531	628	733	846	967
1050	925	808	699	598	505	420	421	422	423	424	425	426	427	428	429	430	431	432	433	434	435	436	437	438	439	440	441	530	627	732	845	966
1051	926	809	700	599	506	507	508	509	510	511	512	513	514	515	516	517	518	519	520	521	522	523	524	525	526	527	528	529	626	731	844	965
1052	927	810	701	600	601	602	603	604	605	606	607	608	609	610	611	612	613	614	615	616	617	618	619	620	621	622	623	624	625	730	843	964
1053	928	811	702	703	704	705	706	707	708	709	710	711	712	713	714	715	716	717	718	719	720	721	722	723	724	725	726	727	728	729	842	963
1054	929	812	813	814	815	816	817	818	819	820	821	822	823	824	825	826	827	828	829	830	831	832	833	834	835	836	837	838	839	840	841	962
1055	930	931	932	933	934	935	936	937	938	939	940	941	942	943	944	945	946	947	948	949	950	951	952	953	954	955	956	957	958	959	960	961
1056	1057	1058	1059	1060	1061	1062	1063	1064	1065	1066	1067	1068	1069	1070	1071	1072	1073	1074	1075	1076	1077	1078	1079	1080	1081	1082	1083	1084	1085	1086	1087	1088

Το σύνολο όλων των πρώτων αριθμών συνήθως συμβολίζεται με P.

Θεμελιώδες θεώρημα της αριθμητικής

Η τεράστια σημασία των πρώτων αριθμών για τη θεωρία αριθμών και τα μαθηματικά γενικότερα πηγάζει από το θεμελιώδες θεώρημα της αριθμητικής, το οποίο αναφέρει ότι κάθε θετικός ακέραιος του 1 μπορεί να γραφεί ως γινόμενο ενός ή περισσότερων πρώτων κατά ένα μοναδικό τρόπο εκτός από τη σειρά διάταξης των παραγόντων που είναι πρώτοι αριθμοί. Οι πρώτοι μπορούν έτσι να θεωρηθούν βασικά δομικά στοιχεία των φυσικών αριθμών. Για παράδειγμα:

23244 = 2 · 2 · 3 · 13 · 149 = 2² · 3 · 13 · 149. (2² συμβολίζει το τετράγωνο ή τη δεύτερη δύναμη του 2.)

Όπως και στο παραπάνω παράδειγμα, ο ίδιος παράγοντας πρώτου αριθμού μπορεί να εμφανίζεται παραπάνω από μία φορές. Μια αποσύνθεση:

n = p₁ · p₂ · ... · p_t

ενός αριθμού n σε (πεπερασμένου πλήθους) πρώτους παράγοντες p₁, p₂, ..., p_t ονομάζεται παραγοντοποίηση του n σε πρώτους παράγοντες. Το θεμελιώδες θεώρημα της αριθμητικής μπορεί να επαναδιατυπωθεί έτσι, ώστε να λέει ότι κάθε παραγοντοποίηση σε πρώτους αριθμούς θα είναι πανομοιότυπη εκτός από τη σειρά διάταξης των παραγόντων. Έτσι, μολονότι υπάρχουν πολλοί αλγόριθμοι παραγοντοποίησης με παράγοντες πρώτους αριθμούς για να το κάνουμε αυτό στην πράξη για μεγαλύτερους αριθμούς, στο τέλος όλοι οι αλγόριθμοι θα αποδίδουν το ίδιο αποτέλεσμα.

Αν p είναι ένας πρώτος αριθμός και ο p διαιρεί ένα γινόμενο αb , όπου α, b είναι ακέραιοι, τότε ισχύει ότι ο p διαιρεί τον α ή ο p διαιρεί τον b. Αυτή η πρόταση είναι γνωστή ως το λήμμα του Ευκλείδη. Το λήμμα του Ευκλείδη χρησιμοποιείται σε μερικές αποδείξεις για να αποδειχθεί η μοναδικότητα της παραγοντοποίησης ενός αριθμού σε πρώτους παράγοντες.

Ο αριθμός 1 δεν είναι πρώτος

Οι αρχαίοι Έλληνες δε θεωρούσαν τον 1 ούτε ως αριθμό κι έτσι δε τον θεωρούσαν ούτε ως πρώτο. Ωστόσο, στο 19ο αιώνα πολλοί μαθηματικοί θεωρούσαν τον 1 ως πρώτο αριθμό. Για παράδειγμα, η λίστα του Ντέρικ Νόρμαν Λέμερ που περιείχε πρώτους αριθμούς ως το 10,006,721 και εκδόθηκε μέχρι και το 1956, άρχιζε με τον 1 ως πρώτο αριθμό. Λέγεται ότι ο Ανρί Λεμπέσγκ είναι ο τελευταίος επαγγελματίας μαθηματικός που θεωρεί τον 1 ως πρώτο αριθμό. Παρόλο που ένα μεγάλο τμήμα των μαθηματικών είναι σωστό με τη θεωρία του 1 ως πρώτου αριθμού, το παραπάνω θεμελιώδες θεώρημα της αριθμητικής δε στέκει όπως είναι διατυπωμένο. Για παράδειγμα, ο αριθμός 15 μπορεί να παραγοντοποιηθεί ως 3 · 5 ή 1 · 3 · 5. Αν ο 1 ήταν πρώτος, τότε αυτές οι δύο εκφράσεις θα παρίσταναν διαφορετικές παραγοντοποιήσεις του 15 σε πρώτους αριθμούς κι έτσι το θεώρημα θα έπρεπε να τροποποιηθεί. Επιπρόσθετα, οι πρώτοι αριθμοί έχουν αρκετές ιδιότητες, τις οποίες ο αριθμός 1 δεν έχει, όπως τη σχέση του αριθμού με την αντίστοιχη τιμή του στη συνάρτηση του Όιλερ ή στη συνάρτηση του αθροίσματος των διαιρετών.

Ιστορία

Υπάρχουν ενδείξεις σε διασωθείσες επιγραφές των αρχαίων Αιγυπτίων ότι είχαν κάποια γνώση πρώτων αριθμών: οι επεκτάσεις του αιγυπτιακού κλάσματος στον πάπυρο του Ριντ, για παράδειγμα, έχουν αρκετά διαφορετικούς τύπους για πρώτους και για σύνθετους αριθμούς. Ωστόσο, οι πιο πρώιμες διασωθείσες επιγραφές σαφούς μελέτης των πρώτων αριθμών προέρχονται από τους αρχαίους Έλληνες. Τα στοιχεία του Ευκλείδη (περίπου στο 300 π.Χ.) περιέχουν σημαντικά θεωρήματα για τους πρώτους αριθμούς, συμπεριλαμβανομένων της απειρίας των πρώτων αριθμών και του θεμελιώδους θεωρήματος της αριθμητικής. Ο Ευκλείδης επίσης απέδειξε πώς μπορούμε να κατασκευάσουμε έναν τέλειο αριθμό από ένα πρώτο Μερσέν αριθμό. Το κόσκινο του Ερατοσθένη, το οποίο αποδίδεται στον Ερατοσθένη, είναι μια απλή μέθοδος να υπολογίσουμε τους πρώτους, παρόλο που οι μεγάλοι πρώτοι δεν υπολογίζονται σήμερα με τους υπολογιστές με αυτό τον τρόπο.

Μετά τους Έλληνες, λίγα πράγματα συνέβησαν με την έρευνα των πρώτων αριθμών μέχρι τον 17ο αιώνα. Το 1640 ο Πιέρ ντε Φερμά διατύπωσε (χωρίς απόδειξη) το μικρό θεώρημα του Φερμά (αργότερα αποδείχθηκε από τους Λάιμπνιτς και Όιλερ). Ο Φερμά υπέθεσε ότι όλοι οι αριθμοί της μορφής 2²ⁿ + 1 είναι πρώτοι (αυτοί οι αριθμοί ονομάζονται αριθμοί Φερμά) και το επαλήθευσε αυτό μέχρι και για n = 4 (ή 2¹⁶ + 1). Αλλά ο αμέσως επόμενος αριθμός Φερμά 2³² + 1 είναι σύνθετος (ένας από τους παράγοντες του που είναι πρώτος αριθμός είναι ο 641), όπως ανακάλυψε αργότερα ο Όιλερ και μάλιστα δεν υπάρχουν παραπάνω γνωστοί αριθμοί Φερμά, οι οποίοι είναι πρώτοι. Ο Γάλλος καλόγερος Μερσέν μελέτησε τους πρώτους αριθμούς της μορφής 2^p - 1, όπου p είναι πρώτος. Αυτοί οι αριθμοί ονομάζονται πρώτοι αριθμοί Μερσέν προς τιμή του.

Το έργο του Όιλερ στη θεωρία αριθμών περιλαμβάνει πολλά συμπεράσματα για τους πρώτους αριθμούς. Ο Όιλερ απέδειξε ότι η άπειρη σειρά 1/2 + 1/3 + 1/5 + 1/7 + 1/11 + ... αποκλίνει. Το 1747 έδειξε ότι οι άρτιοι τέλειοι αριθμοί είναι ακριβώς οι ακέραιοι της μορφής 2^p-1(2^p − 1), όπου ο δεύτερος παράγοντας είναι ένας πρώτος Μερσέν αριθμός.

Στις αρχές του 19ου αιώνα, οι Λεζάντρ και Γκάους ανεξάρτητα υπέθεσαν ότι καθώς το x τείνει στο άπειρο, το πλήθος των πρώτων αριθμών μέχρι και το x είναι ασύμπτωτο στο κλάσμα x/ln(x), όπου ln(x) είναι ο φυσικός λογάριθμος του x. Στις ιδέες του ο Ρίμαν για τη συνάρτηση ζήτα, τις οποίες εξέδωσε το 1859, σχεδίαζε ένα πρόγραμμα που θα οδηγούσε σε μια απόδειξη του θεωρήματος των πρώτων αριθμών. Αυτό το περίγραμμα ολοκληρώθηκε από τους Χάνταμαρντ και ντε λα Βαλέ Ποσίν, οι οποίοι ανεξάρτητα απέδειξαν το θεώρημα των πρώτων αριθμών το 1896.

Δε γίνεται να αποδείξουμε ότι ένας μεγάλος αριθμός είναι πρώτος με τη δοκιμαστική διαίρεση. Πολλοί μαθηματικοί έχουν εργαστεί στην εύρεση τεχνικών για να αποδειχτεί αν ένας μεγάλος αριθμός είναι πρώτος, αλλά συχνά αυτές οι τεχνικές περιορίζονται σε συγκεκριμένες μορφές αριθμών. Παραδείγματα τέτοιων τεχνικών είναι το τεστ του Πέπιν για τους αριθμούς Φερμά (1877), το θεώρημα του Προθ (γύρω στο 1878), ο έλεγχος των Λούκας-Λέμερ (1856) και το γενικευμένο τεστ πρώτων αριθμών του Λούκας. Πιο πρόσφατοι αλγόριθμοι, όπως οι APRT-CL, ECPP και AKS δουλεύουν για όλους τους αριθμούς, αλλά παραμένουν πολύ πιο αργοί.

Για ένα μεγάλο χρονικό διάστημα, οι πρώτοι αριθμοί θεωρούνταν ότι είχαν εξαιρετικά περιορισμένη εφαρμογή έξω από τα καθαρά μαθηματικά: αυτό άλλαξε τη δεκαετία του 1970, όταν οι έννοιες της κρυπτογραφίας δημοσίου κλειδιού ανακαλύφθηκαν, στην οποία κρυπτογράφηση δημόσιου κλειδιού οι πρώτοι αριθμοί αποτελούσαν τη βάση των πρώτων αλγορίθμων, όπως τον κρυπτογραφικό αλγόριθμο RSA.

Από το 1951 όλοι οι μεγαλύτεροι πρώτοι αριθμοί έχουν βρεθεί από τους ηλεκτρονικούς υπολογιστές. Η έρευνα για όλο και μεγαλύτερους πρώτους αριθμούς έχει προκαλέσει ενδιαφέρον και έξω από τους μαθηματικούς κύκλους. Η μεγάλη διαδικτυακή έρευνα πρώτων Μερσέν αριθμών και άλλες εργασίες σε παράλληλα και κατανεμημένα συστήματα πληροφορικής για την εύρεση μεγάλων πρώτων αριθμών έχουν γίνει διάσημες τα τελευταία δέκα με δεκαπέντε χρόνια, ενώ οι μαθηματικοί συνεχίζουν να παλεύουν με τη θεωρία των πρώτων αριθμών.

Πλήθος πρώτων αριθμών

Υπάρχουν άπειροι το πλήθος πρώτοι αριθμοί. Ένας άλλος τρόπος για να πούμε το ίδιο είναι ότι η ακολουθία

2, 3, 5, 7, 11, 13, ...

των πρώτων αριθμών δεν τελειώνει ποτέ. Αυτή η πρόταση ονομάζεται θεώρημα του Ευκλείδη προς τιμή του αρχαίου Έλληνα μαθηματικού Ευκλείδη, αφού η πρώτη γνωστή απόδειξη για αυτή την πρόταση αποδίδεται σε αυτόν. Πολλές περισσότερες αποδείξεις της απειρίας των πρώτων αριθμών είναι γνωστές, όπως μια αναλυτική απόδειξη από τον Όιλερ, η απόδειξη του Γκόλντμπαχ βασισμένη στους αριθμούς Φερμά, η απόδειξη του Φούρστενμπεργκ χρησιμοποιώντας γενική τοπολογία και η κομψή απόδειξη του Κούμερ.

Η απόδειξη του Ευκλείδη

Έστω ένα πεπερασμένο σύνολο S πρώτων αριθμών. Η ιδέα - κλειδί είναι να θεωρήσουμε το γινόμενο όλων αυτών των αριθμών συν ένα:

$N=1+\prod _{p\in S}p.$

Όπως κάθε άλλος φυσικός αριθμός, ο Ν μπορεί να διαιρεθεί από τουλάχιστον ένα πρώτο αριθμό (είναι πιθανό ο Ν να είναι πρώτος).

Κανένας από τους πρώτους αριθμούς οι οποίοι διαιρούν τον Ν δεν μπορεί να είναι στοιχείο του πεπερασμένου συνόλου S των πρώτων αριθμών με το οποίο ξεκινήσαμε, επειδή διαιρώντας τον Ν με οποιοδήποτε από αυτούς τους πρώτους αριθμούς αφήνει υπόλοιπο 1. Επομένως, οι πρώτοι από τους οποίους ο Ν διαιρείται είναι επιπλέον πρώτοι εκτός από αυτόν με τον οποίο ξεκινήσαμε. Έτσι κάθε πεπερασμένο σύνολο πρώτων αριθμών μπορεί να επεκταθεί σε ένα μεγαλύτερο πεπερασμένο σύνολο πρώτων αριθμών.

Συχνά αναφέρεται εσφαλμένα ότι ο Ευκλείδης ξεκινάει με την υπόθεση ότι αρχικά το σύνολο που θεωρούμε περιέχει όλους τους πρώτους αριθμούς, καταλήγοντας σε μια αντίφαση ή ότι το σύνολο περιέχει ακριβώς τους n μικρότερους πρώτους αριθμούς και όχι κάθε πεπερασμένο σύνολο πρώτων αριθμών. Σήμερα, το γινόμενο των μικρότερων n πρώτων αριθμών συν ένα συμβατικά ονομάζεται ο n-οστός αριθμός του Ευκλείδη.

Η αναλυτική απόδειξη του Όιλερ

Στην απόδειξη του Όιλερ χρησιμοποιείται το άθροισμα των αντίστροφων των πρώτων αριθμών,

$S(p)={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+\cdots +{\frac {1}{p}}.$

Αυτό το άθροισμα γίνεται μεγαλύτερο από κάθε πραγματικό αριθμό με την προϋπόθεση ότι ο p είναι αρκετά μεγάλος. Αυτό δείχνει ότι υπάρχουν απείρως πολλοί πρώτοι αριθμοί, αφού ειδάλλως αυτό το άθροισμα θα μεγάλωνε μόνο μέχρι να φτάσουμε στο μεγαλύτερο πρώτο αριθμό p. Η αύξηση του S(p) υπολογίζεται από το δεύτερο θεώρημα του Μερσέν. Σε σύγκριση με το παραπάνω άθροισμα, παρατηρούμε ότι το άθροισμα

${\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+{\frac {1}{3^{2}}}+\cdots +{\frac {1}{n^{2}}}=\sum _{i=1}^{n}{\frac {1}{i^{2}}}$

δεν τείνει στο άπειρο, καθώς το n τείνει στο άπειρο. Με αυτή την έννοια, οι πρώτοι αριθμοί εμφανίζονται πιο συχνά από τα τετράγωνα των φυσικών αριθμών. Το θεώρημα του Μπραν αναφέρει ότι το άθροισμα των αντίστροφων δύο διδύμων πρώτων αριθμών,

$\left({{\frac {1}{3}}+{\frac {1}{5}}}\right)+\left({{\frac {1}{5}}+{\frac {1}{7}}}\right)+\left({{\frac {1}{11}}+{\frac {1}{13}}}\right)+\cdots =\sum \limits _{\begin{smallmatrix}p{\text{ πρώτος, }}\\p+2{\text{ πρώτος}}\end{smallmatrix}}{\left({{\frac {1}{p}}+{\frac {1}{p+2}}}\right)},$

είναι πεπερασμένο.

Αναγνώριση πρώτου αριθμού και παραγοντοποίηση ακεραίου

Υπάρχουν ποικίλες μέθοδοι για να προσδιορίσουμε αν ένας αριθμός n είναι πρώτος. Η πιο βασική μέθοδος, η δοκιμαστική διαίρεση, έχει μικρή πρακτική χρησιμότητα επειδή είναι αργή. Ένα τμήμα των σύγχρονων μεθόδων για τον προσδιορισμό αν ένας αριθμός είναι πρώτος είναι εφαρμόσιμο για όλους τους αριθμούς, ενώ οι πιο αποτελεσματικές μέθοδοι είναι διαθέσιμες μόνο για συγκεκριμένες κατηγορίες αριθμών. Οι περισσότερες από αυτές τις μεθόδους λένε μόνο αν ο αριθμός είναι πρώτος ή όχι. Οι μέθοδοι, οι οποίες επιπλέον βρίσκουν και έναν ή περισσότερους παράγοντες του υπό εξέταση αριθμού ονομάζονται αλγόριθμοι παραγοντοποίησης.

Δοκιμαστική διαίρεση

Η πιο βασική μέθοδος ελέγχου αν ένας ακέραιος αριθμός είναι πρώτος ονομάζεται δοκιμαστική διαίρεση. Αυτή η μέθοδος συνίσταται στη διαίρεση του n από κάθε ακέραιο m, ο οποίος είναι του 1 και μικρότερος ή ίσος της τετραγωνικής ρίζας του n. Αν το αποτέλεσμα οποιασδήποτε από αυτές τις διαιρέσεις είναι ακέραιος, τότε ο n δεν είναι πρώτος, ειδάλλως είναι πρώτος αριθμός. Πράγματι, αν n = αb είναι σύνθετος (με α και b ≠ 1), τότε ένας από τους παράγοντες α ή b απαραίτητα το πολύ ίσος με ${\sqrt {n}}$. Για παράδειγμα, για n = 37 οι δοκιμαστικές διαιρέσεις είναι από τους m = 2, 3, 4, 5 και 6. Κανένας από αυτούς τους αριθμούς δε διαιρεί το 37, οπότε ο 37 είναι πρώτος. Αυτός ο τρόπος μπορεί να εφαρμοστεί πιο αποτελεσματικά αν μια ολοκληρωμένη λίστα πρώτων αριθμών μέχρι και ${\sqrt {n}}$ είναι γνωστή - μετά οι δοκιμαστικές διαιρέσεις χρειάζεται να γίνουν μόνο για εκείνους τους m που είναι πρώτοι. Για παράδειγμα, για να ελέγξουμε αν ο 37 είναι πρώτος, μόνο τρεις διαιρέσεις είναι απαραίτητες (m = 2, 3 και 5), αφού οι αριθμοί 4 και 6 είναι σύνθετοι.

Η απλή μέθοδος της δοκιμαστικής διαίρεσης γρήγορα γίνεται μη πρακτική για τον έλεγχο μεγάλων ακεραίων επειδή το πλήθος των πιθανών παραγόντων μεγαλώνει ραγδαία καθώς ο n αυξάνεται. Σύμφωνα με το θεώρημα των πρώτων αριθμών, το οποίο αναλύεται παρακάτω, το πλήθος των πρώτων αριθμών μικρότερων του ${\sqrt {n}}$ είναι της τάξης ${\sqrt {n}}/\ln({\sqrt {n}})$. Για τον μικρότερο πρώτο μεγαλύτερο του 10²⁰, το πλήθος των πρώτων που πρέπει να δοκιμαστούν είναι περίπου 455 εκατομμύρια. Πάρα πολλοί από αυτούς δεν χωράνε σε 32bit (10¹⁰ > 4*10⁹ ≈ 2³²), αλλά ακόμα και αν χωρούσαν θα χρειαζόταν περίπου 4*455 = 910 εκατομμύρια bytes για την αποθήκευσή τους. Εναλλακτικά, χωρίς αποθήκευση πρώτων αριθμών, χρειάζονται περίπου 10 δισεκατομμύρια διαιρέσεις.

Κόσκινα

Ένας αλγόριθμος, ο οποίος αποδίδει όλους τους πρώτους αριθμούς μέχρι ένα δοθέν όριο, όπως απαιτείται στη μέθοδο της δοκιμαστικής διαίρεσης, ονομάζεται κόσκινο πρώτων αριθμών. Το αρχαιότερο παράδειγμα, το κόσκινο του Ερατοσθένη είναι χρήσιμο για σχετικά μικρούς πρώτους αριθμούς. Το σύγχρονο κόσκινο του Άτκιν είναι πιο περίπλοκο, αλλά πιο γρήγορο, όταν βελτιστοποιείται κατάλληλα. Πριν την ανακάλυψη των υπολογιστών, χρησιμοποιούνταν επίσης κατάλογοι πρώτων αριθμών με όρια μέχρι και 10⁷.

Αιτιοκρατική και πιθανοτική αναγνώριση πρώτου

Οι σύγχρονοι έλεγχοι για τους πρώτους αριθμούς διαιρούνται σε δύο κατηγορίες, τους πιθανοτικούς (ή Μόντε Κάρλο) και τους αιτιοκρατικούς (ντετερμινιστικούς) αλγορίθμους. Ο έλεγχος του Φερμά για τους πρώτους αριθμούς βασίζεται στο μικρό θεώρημα του Φερμά. Το θεώρημα αυτό λέει ότι για κάθε πρώτο αριθμό p και για κάθε ακέραιο α, ο οποίος δε διαιρείται από τον p, ο αριθμός a^{p − 1} − 1 διαιρείται από τον p. Έτσι, αν ο αριθμός a^{n − 1} − 1 δε διαιρείται από τον n, τότε ο n δεν μπορεί να είναι πρώτος. Ωστόσο, το αντίστροφο δεν ισχύει. Οι σύνθετοι αριθμοί που περνάνε τον έλεγχο του Φερμά για κάποιο α, ονομάζονται ψευδοπρώτοι στη βάση α. Μάλιστα, υπάρχουν άπειροι σύνθετοι αριθμοί n, οι οποίοι περνούν τον έλεγχου του Φερμά για κάθε α σχετικά πρώτο με τον n (αριθμοί Καρμάικλ). Ο δημοφιλής αλγόριθμος Miller-Rabin χρησιμοποιεί μια παραλλαγή του ελέγχου του Φερμά και ελέγχοντας ένα πλήθος από τυχαία α, εγγυάται ότι ένας αριθμός που περνάει τον έλεγχο για κάθε α είναι πρώτος με μεγάλη στατιστική βεβαιότητα. Η στατιστική βεβαιότητα είναι ανάλογη του πλήθους των τυχαίων α που χρησιμοποιεί ο αλγόριθμος.

Οι αιτιοκρατικοί (ντετερμινιστικοί) αλγόριθμοι αναγνωρίζουν έναν αριθμό ως πρώτο αν και μόνον αν είναι πρώτος. Για πρακτικά μεγέθη, ο ποιο γρήγορος αλγόριθμος αυτής της κατηγορίας χρησιμοποιεί την απόδειξη της ελλειπτικής καμπύλης (ECPP) για να αναγνωρίσει ένα αριθμό ως πρώτο. Η χρονική πολυπλοκότητα του αλγορίθμου αυτού είναι κατά μέσον όρο πολυωνυμική, αλλά δεν είναι γνωστό αν αυτό συμβαίνει και στη χειρότερη περίπτωση. Ο αλγόριθμος AKS είναι μεγάλης θεωρητικής σημασίας καθώς αποδεικνύει ότι το πρόβλημα της αναγνώρισης πρώτου αριθμού έχει πολυωνυμική χρονική πολυπλοκότητα στη χειρότερη περίπτωση. Είναι όμως κατά πολύ αργότερος από τον ECCP για πρακτικά μεγέθη. Οι αιτιοκρατικές μέθοδοι είναι τυπικά πιο αργές από τις πιθανοτικές κι έτσι οι τελευταίες εφαρμόζονται πρώτες πριν χρησιμοποιηθούν οι πιο χρονοβόρες αιτιοκρατικές μέθοδοι.

Ειδικοί αλγόριθμοι και ο γνωστός πρώτος αριθμός

Κατασκευή ενός κανονικού πενταγώνου. Ο 5 είναι ένας πρώτος αριθμός Φερμά.

Εκτός από τις παραπάνω δοκιμές για τους πρώτους αριθμούς για κάθε φυσικό αριθμό n, ένα πλήθος πολύ περισσότερο αποτελεσματικών μεθόδων για πρώτους αριθμούς είναι διαθέσιμο για συγκεκριμένους αριθμούς. Για παράδειγμα, για να εκτελεστεί η μέθοδος του Lucas για τους πρώτους απαιτείται η γνώση των παραγόντων που είναι πρώτοι αριθμοί του αριθμού n - 1, ενώ η μέθοδος των Λούκας-Λέμερ για τους πρώτους αριθμούς απαιτεί τους παράγοντες που είναι πρώτοι αριθμοί του αριθμού n + 1 ως δεδομένο. Για παράδειγμα, αυτές οι μέθοδοι μπορούν να εφαρμοστούν για να ελέγξουμε αν οι αριθμοί

n! ± 1 = 1 · 2 · 3 · ... · n ± 1

είναι πρώτοι. Οι πρώτοι αριθμοί αυτής της μορφής είναι γνωστοί ως παραγοντικοί πρώτοι αριθμοί. Άλλοι πρώτοι αριθμοί, όπου είτε ο p + 1 ή ο p - 1 είναι μιας συγκεκριμένης μορφής περιλαμβάνουν τους πρώτους αριθμούς Σόφι Ζερμέν (πρώτοι αριθμοί της μορφής 2p + 1, όπου p είναι πρώτος), τους αρχέγονους πρώτους αριθμούς, τους πρώτους αριθμούς του Φερμά και τους πρώτους αριθμούς του Μερσέν, οι οποίοι είναι πρώτοι αριθμοί της μορφής 2^p - 1, όπου p είναι ένας τυχαίος πρώτος αριθμός. Η μέθοδος των Λούκας-Λέμερ είναι εξαιρετικά γρήγορη για τους πρώτους αριθμούς της μορφής αυτής. Για το λόγο αυτό ο γνωστός πρώτος αριθμός έχει γίνει σχεδόν ένας πρώτος Μερσέν από τότε που ανακαλύφθηκαν οι υπολογιστές.

Οι πρώτοι αριθμοί Φερμά είναι της μορφής

F_k = 2^2k + 1,

όπου k είναι ένας τυχαίος φυσικός αριθμός. Έτσι ονομάστηκαν οι αριθμοί αυτής της μορφής, αφού ο Πιέρ ντε Φερμά υπέθεσε ότι όλοι οι F_k είναι πρώτοι. Η πρόταση αυτή βασίστηκε στο γεγονός ότι οι οι πέντε πρώτοι τέτοιοι αριθμοί 3, 5, 17, 257 και 65,537 είναι πρώτοι. Ωστόσο, ο F₅=4294967297=641×6700417 είναι σύνθετος και το ίδιο συμβαίνει για τους υπόλοιπους αριθμούς Φερμά, οι οποίοι έχουν ελεγχθεί από το 2011. Ένα κανονικό n-γώνιο είναι κατασκευάσιμο χρησιμοποιώντας χάρακα και διαβήτη αν και μόνο αν

n = 2ⁱ · m,

όπου m είναι ένας οποιοσδήποτε αριθμός από τους πρώτους Φερμά αριθμούς και i είναι ένας οποιοσδήποτε φυσικός αριθμός ή το μηδέν.

Ο παρακάτω πίνακας δίνει τους μεγαλύτερους γνωστούς πρώτους αριθμούς των προαναφερθέντων τύπων. Κάποιοι από αυτούς τους πρώτους βρέθηκαν χρησιμοποιώντας κατανεμημένα συστήματα πληροφορικής.

Τύπος	Πρώτος αριθμός	Πλήθος δεκαδικών ψηφίων	Ημερομηνία	Ανακαλύφθηκε από
πρώτος Μερσέν	282.589.933 − 1	24.862.048	Δεκέμβριος 2018	Great Internet Mersenne Prime Search
όχι πρώτος Μερσέν (αριθμός Προθ)	$10223\cdot 2^{31172165}+1$ ψηφίων.	9.383.761	6 Νοεμβρίου 2016	Seventeen or Bust
παραγοντικός πρώτος	150209! + 1	712,355	Οκτώβριος 2011	PrimeGrid
αρχέγονος πρώτος	1098133# - 1	476,311	Μάρτιος 2012	PrimeGrid
δίδυμοι πρώτοι αριθμοί	2.996.863.034.895 * 21290000 ± 1 .	388.342	Σεπτέμβριος 2016	PrimeGrid

Εύρεση πρώτων

Κόσκινο του Ερατοσθένη

Η εύρεση των πρώτων αριθμών απασχόλησε από την αρχαιότητα τους μαθηματικούς. Ένας από τους πιο απλούς αλλά και αργούς τρόπους για (μαζική) εύρεση πολλών πρώτων είναι το λεγόμενο κόσκινο του Ερατοσθένη: Στο σύνολο των φυσικών αριθμών - πρακτικά έως κάποιο μεγάλο αριθμό Ν - αρχίζουμε και αποκλείουμε πρώτα τα πολλαπλάσια του 2 μετά τα πολλαπλάσια του επόμενου μη διαγραμμένου αριθμού κ.ο.κ. έως το Ν. Παρατηρούμε ότι όλο και λιγότερους αριθμούς θα βρίσκουμε προς διαγραφή. Οι αριθμοί που θα απομείνουν είναι όλοι πρώτοι. Το κόσκινο του Ερατοσθένη είναι ένας αργός αλγόριθμος για το αν ένας συγκεκριμένος αριθμός Ν είναι πρώτος ή όχι, διότι μεταξύ άλλων απαιτεί ουσιαστικά και την εύρεση όλων των πρώτων μικρότερων ίσων του ${\sqrt {N}}$ (αν ένας αριθμός Ν δεν έχει διαιρέτες μικρότερους ίσους του ${\sqrt {N}}$, τότε είναι πρώτος).

Οπτικό κόσκινο Matiyasevich-Stechkin

Στις 14 Φεβρουαρίου 1999 οι Γιούρι Ματιγιάσεβιτς και Μπόρις Στέκιν δημοσίευσαν στο διαδίκτυο το οπτικό κόσκινο των πρώτων αριθμών. Τα σημεία της παραβολής $x=y^{2}$ με ακέραιες συντεταγμένες ορίζουν χορδές που τέμνουν τον οριζόντιο άξονα x΄x σε σημεία της μορφής (αβ,0) όπου α,β ακέραιοι κι επομένως σαρώνουν όλους τους σύνθετους θετικούς ακέραιους.

Αλγόριθμοι εύρεσης πρώτων

Παρατίθενται μερικοί αλγόριθμοι (κατά σειρά ταχύτητας ή και απλότητας) για την εύρεση αν ο Ν>=2 είναι πρώτος. Η σειρά επίσης αυτών των αλγορίθμων είναι παιδευτική για την εισαγωγή σε μια σειρά από προγράμματα για ηλεκτρονικούς υπολογιστές.

Απλός 1 - από τον ορισμό του πρώτου αριθμού

• Εξετάζουμε διαδοχικά όλους τους ακέραιους Μ < Ν
• Μόλις βρεθεί διαιρέτης του Ν σταματάμε και ο Ν δεν είναι πρώτος
• Αν εξαντληθούν οι Μ χωρίς να βρεθεί διαιρέτης, τότε ο Ν είναι πρώτος

Απλός 2

Βασιζόμενοι στην παρατήρηση ότι κανένας αριθμός Ν δεν έχει διαιρέτη μεγαλύτερο του Ν/2, τροποποιούμε τον παραπάνω αλγόριθμο εξετάζοντας όλους τους αριθμούς Μ < Ν/2, διπλασιάζοντας έτσι την ταχύτητα σε σχέση με τον "Απλό 1".

Απλός 3

Παρατηρούμε ότι αν ένας αριθμός Ν δεν είναι πρώτος τότε έχει (τουλάχιστον) δύο διαιρέτες μεγαλύτερους από 1. Σε αυτήν την περίπτωση τουλάχιστον ένας διαιρέτης είναι μικρότερος από την τετραγωνική ρίζα του αριθμού. Τροποποιούμε τον αλγόριθμο 2 εξετάζοντας όλους τους αριθμούς Μ που είναι μικρότεροι από την τετραγωνική ρίζα του N, αν η τελευταία δεν είναι ακέραιος. Αλλιώς ο αριθμός δεν είναι πρώτος, επειδή τον διαιρεί και η τετραγωνική του ρίζα.

Απλός 4

Εφαρμόζοντας το Θεώρημα του Ουίλσον μπορούμε να εξετάσουμε, αν ένας αριθμός Ν είναι πρώτος ή όχι. Σύμφωνα με το θεώρημα αυτό ο Ν είναι πρώτος αν και μόνο αν ισχύει

$(N-1)!\ \equiv \ -1\ ({\mbox{mod}}\ N),$

αν δηλαδή το υπόλοιπο της διαίρεσης του Ν-1 παραγοντικό με το Ν, είναι ίσο με το υπόλοιπο της διαίρεσης του -1 με το N.

Η μέθοδος αυτή δεν εφαρμόζεται για μεγάλο Ν, αφού είναι δύσκολο να υπολογιστεί το παραγοντικό.

Ο μεγαλύτερος γνωστός πρώτος αριθμός

Τον Οκτώβριο του 2024 ο μεγαλύτερος γνωστός πρώτος αριθμός είναι πλέον ο είναι ο 2^136279841 − 1, ο οποίος έχει 41.024.320 ψηφία. Βρέθηκε τον Οκτώβριο του 2024 από το Great Internet Mersenne Prime Search (GIMPS).

Δεύτερος είναι ο 2^82589933 − 1, ο οποίος έχει 24.862.048 ψηφία. Βρέθηκε τον Δεκέμβριο του 2018 από το Great Internet Mersenne Prime Search (GIMPS).

$M_{51}=2^{82,589,933}-1$ (M82589933)

Ο τρίτος πρώτος είναι ο 2^77.232.917 − 1, ο οποίος έχει 23.249.425 ψηφία. Βρέθηκε τον Δεκέμβριο του 2017 από το Great Internet Mersenne Prime Search (GIMPS).

$M_{50}=2^{77,232,917}-1$ (M77232917)

Ο τέταρτος πρώτος είναι ο :

$M_{49}=2^{74,207,281}-1$ (M74207281), ο οποίος ανακαλύφθηκε μέσω του GIMPS τον Ιανουάριο του 2016 και έχει 22.338.618 ψηφία.

και η ανακάλυψη του, έγινε στις 25 Ιανουαρίου 2013, μέσω του διαδικτυακού προγράμματος κατανεμημένης επεξεργασίας GIMPS (Great Internet Mersenne Prime Search). Ο αριθμός αυτός έχει 17.425.179 ψηφία (ο δεύτερος με πάνω από 10 εκατομμύρια ψηφία) και έχει την πρόσθετη ιδιότητα να είναι ο 48ος Μερσέν πρώτος (Mersenne prime) που ανακαλύφθηκε. Ο 47ος Μερσέν πρώτος, ο 2^43,112,609 − 1, ανακαλύφθηκε στις 25 Αυγούστου του 2008.

Στο πρόσφατο παρελθόν, όλοι οι πρώτοι που ανακαλύφθηκαν ήταν Μερσέν πρώτοι.

Επίσης, για τον πρώτο πρώτο αριθμό που ανακαλύφθηκε και είχε πάνω από 10.000.000 ψηφία, δόθηκαν 100.000 δολάρια.

Ιδιότητες πρώτων αριθμών

• Αν ο p είναι πρώτος και διαιρεί το γινόμενο ab για κάποιους ακέραιους a, b τότε ο p διαιρεί το a ή το b. (Ευκλείδης)

• Αν p πρώτος και a ακέραιος, τότε το a^p − a διαιρείται από το p (Μικρό Θεώρημα του Φερμά).

• Ένας ακέραιος p > 1 είναι πρώτος αν και μόνο αν p - 1 παραγοντικό + 1 δηλ. το (p − 1)! + 1 διαιρείται από το p (Θεώρημα του Ουίλσον).

• Όλοι οι πρώτοι αριθμοί στο δεκαδικό σύστημα, εκτός του 2 και του 5, έχουν ως τελευταίο ψηφίο ένα από τα 1, 3, 7 ή 9, διότι οι αριθμοί που τελειώνουν σε 0, 2, 4, 6 και 8 είναι πολλαπλάσια του 2 ενώ οι αριθμοί που τελειώνουν σε 0 ή 5 είναι πολλαπλάσια του 5.

Κατανομή

Η κατανομή των πρώτων αριθμών γενικά, όπως η ερώτηση πόσοι πρώτοι αριθμοί είναι μικρότεροι από ένα δοθέντα πρώτο αριθμό, πόσο μεγάλο είναι το όριο, περιγράφεται από το θεώρημα των πρώτων αριθμών, αλλά δεν είναι γνωστός κανένας τύπος που να είναι αποτελεσματικός για το n-οστό πρώτο αριθμό.

Υπάρχουν αυθαίρετα μεγάλες ακολουθίες διαδοχικών μη πρώτων αριθμών, όπως για κάθε θετικό ακέραιο αριθμό n οι n διαδοχικοί ακέραιοι από (n + 1)! + 2 ως (n + 1)! + n + 1 (συμπεριλαμβανομένης και της τελικής τιμής) είναι όλοι σύνθετοι αριθμοί (αφού (n + 1)! + k διαιρείται από τον k για k από 2 ως n + 1).

Το θεώρημα του Ντίριχλετ για τις αριθμητικές προόδους, στη βασική του μορφή, ισχυρίζεται ότι τα γραμμικά πολυώνυμα

p(n) = α + bn

με τους σχετικά πρώτους α και b να παίρνουν άπειρα πολλές τιμές πρώτων αριθμών. Ισχυρότερες μορφές του θεωρήματος αναφέρουν ότι το άθροισμα των τιμών που επιστρέφει το πολυώνυμο αυτών των τιμών που είναι πρώτοι αριθμοί αποκλίνει και αυτές οι διαφορές που υπάρχουν στα πολυώνυμα με το ίδιο b έχουν περίπου τις ίδιες αναλογίες των πρώτων αριθμών.

Η αντίστοιχη ερώτηση για τα τετραγωνικά πολυώνυμα είναι λιγότερο κατανοητή.

Τύποι των πρώτων αριθμών

Δεν υπάρχει κανένας γνωστός αποτελεσματικός τύπος για τους πρώτους αριθμούς. Για παράδειγμα, το θεώρημα του Μιλς και ένα θεώρημα του Ράιτ ισχυρίζονται ότι υπάρχουν πραγματικές σταθερές Α > 1 και μ, τέτοιες ώστε

$\left\lfloor A^{3^{n}}\right\rfloor {\text{ and }}\left\lfloor 2^{\dots ^{2^{2^{\mu }}}}\right\rfloor$

να είναι πρώτοι αριθμοί για κάθε φυσικό αριθμό n. Εδώ $\lfloor -\rfloor$ αντιπροσωπεύει ακέραιο μέρος της έκφρασης, δηλαδή το μεγαλύτερο ακέραιο που δεν είναι από τον αριθμό που είναι στις αγκύλες. Ο τελευταίος τύπος μπορεί να αποδειχθεί χρησιμοποιώντας το αξίωμα του Μπέρτραντ (αποδεδειγμένο πρώτα από τον Παφνούτι Λβόβιτς Τσέμπισσιοφ), το οποίο αναφέρει ότι πάντα υπάρχει τουλάχιστον ένας πρώτος αριθμός p με n < p < 2n - 2, για κάθε φυσικό αριθμό n > 3. Ωστόσο, για να υπολογίσουμε τον Α ή τον μ απαιτείται η γνώση των απείρως πολλών πρώτων αριθμών με τους οποίους θα ξεκινήσουμε. Ένας άλλος τύπος βασίζεται στο θεώρημα του Ουίλσον και παράγει τον αριθμό 2 πολλές φορές και όλους τους άλλους πρώτους αριθμούς ακριβώς μία φορά.

Δεν υπάρχει κανένα μη σταθερό πολυώνυμο, ακόμη και σε αρκετές μεταβλητές, οι οποίες παίρνουν ως τιμές μόνο πρώτους αριθμούς. Ωστόσο, υπάρχει ένα σύνολο διοφαντικών εξισώσεων σε 9 μεταβλητές και μια παράμετρος με την εξής ιδιότητα: η παράμετρος είναι πρώτος αριθμός αν και μόνο αν το σύστημα που προκύπτει από τις εξισώσεις έχει μία λύση στους φυσικούς αριθμούς. Αυτό θα μπορούσε να χρησιμοποιηθεί για να αποκτήσει ένα απλό τύπο με την ιδιότητα ότι όλες οι θετικές τιμές του είναι πρώτοι αριθμοί.

Πλήθος των πρώτων αριθμών κάτω από ένα δοθέντα αριθμό

Ένα διάγραμμα που απεικονίζει την π(n) (μπλε), την n/ln(n) (πράσινη) και την Li(n) (κόκκινη)

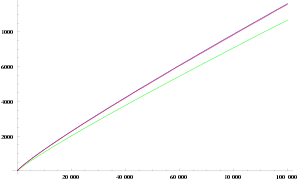
Η συνάρτηση που καταμετράει τους πρώτους αριθμούς π(n) ορίζεται ως το πλήθος των πρώτων αριθμών μέχρι και τον n. Για παράδειγμα π(11) = 5, αφού υπάρχουν πέντε πρώτοι αριθμοί μικρότεροι ή ίσοι του 11. Υπάρχουν γνωστοί αλγόριθμοι για να υπολογίσουμε τις ακριβείς τιμές της συνάρτησης π(n) πιο γρήγορα από ότι να υπολογίζαμε αν κάθε αριθμός είναι πρώτος μέχρι και τον n. Το θεώρημα των πρώτων αριθμών αναφέρει ότι η π(n) δίνεται περίπου από τον τύπο

$\pi (n)\approx {\frac {n}{\ln n}},$,

με την έννοια ότι η αναλογία της π(n) με το κλάσμα του δεξιού μέλους τείνει στο 1, όταν ο n τείνει στο άπειρο. Αυτό συνεπάγεται ότι η πιθανότητα ένας αριθμός μικρότερος του n να είναι πρώτος είναι (περίπου) αντιστρόφως ανάλογη του πλήθους των ψηφίων του n. Ένας πιο ακριβής υπολογισμός για την π(n) δίνεται από το λογαριθμικό ολοκλήρωμα

$\operatorname {Li} (n)=\int _{2}^{n}{\frac {dt}{\ln t}}.$

Το θεώρημα πρώτων αριθμών συνεπάγεται ότι υπολογίζει το μέγεθος του n-οστού πρώτου αριθμού p_n (δηλαδή p₁ = 2, p₂ = 3, κ.ο.κ.) : μέχρι ένα οριοθετημένο παράγοντα, ο p_n αυξάνεται όπως η nlog(n). Πιο συγκεκριμένα, τα κενά των πρώτων αριθμών,δηλαδή οι διαφορές p_n - p_n-1 των δύο διαδοχικών πρώτων αριθμών, γίνονται αυθαίρετα μεγάλες. Αυτή η τελευταία πρόταση μπορεί επίσης να διατυπωθεί με ένα πιο στοιχειώδη τρόπο σημειώνοντας ότι η ακολουθία n! + 2, n! + 3, …, n! + n αποτελείται από n - 1 σύνθετους αριθμούς, για κάθε φυσικό αριθμό n.

Αριθμητικές πρόοδοι

Μια αριθμητική πρόοδος είναι ένα σύνολο φυσικών αριθμών, οι οποίοι δίνουν το ίδιο υπόλοιπο, όταν διαιρούνται από κάποιους σταθερούς αριθμούς q, οι οποίοι ονομάζονται μέτρο. Για παράδειγμα

3, 12, 21, 30, 39, ...,

είναι μια αριθμητική πρόοδος μέτρου q = 9. Εκτός από το 3, κανείς από αυτούς τους αριθμούς δεν είναι πρώτος, αφού 3 + 9n = 3(1 + 3n), έτσι ώστε οι υπόλοιποι αριθμοί της προόδου αυτής είναι όλοι σύνθετοι. (Σε γενικές γραμμές, όλοι οι πρώτοι αριθμοί μεγαλύτεροι του q είναι της μορφής q# · n + m, όπου 0 < m < q# και ο m δεν έχει κανένα παράγοντα πρώτο αριθμό ≤ q.) Έτσι, η πρόοδος

α, α + q, α + 2q, α + 3q, ...

απείρως πολλούς πρώτους αριθμούς, μόνο όταν οι α και q είναι σχετικοί πρώτοι αριθμοί, δηλαδή ο μέγιστος κοινός τους διαιρέτης είναι το ένα. Αν ικανοποιείται αυτή η αναγκαία συνθήκη, τότε το θεώρημα του Ντίριχλετ για τις αριθμητικές προόδους ισχυρίζεται ότι η πρόοδος περιέχει απείρως πολλούς πρώτους αριθμούς. Η εικόνα παρακάτω απεικονίζει την πρόοδο με q = 9: οι αριθμοί είναι τυλιγμένοι γύρω μέχρι να περάσει ένα πολλαπλάσιο του 9. Οι πρώτοι αριθμοί είναι μαρκαρισμένοι με κόκκινο χρώμα. Οι σειρές(= πρόοδοι) που αρχίζουν με α = 3, 6 ή 9 περιέχουν το πολύ ένα πρώτο αριθμό. Σε όλες τις άλλες σειρές (α = 1, 2, 4, 5, 7 και 8) υπάρχουν απείρως πολλοί πρώτοι αριθμοί. Επιπλέον, οι πρώτοι αριθμοί κατανέμονται ισομερώς μεταξύ αυτών των σειρών σε όλη τη ροή - η πυκνότητα των πρώτων αριθμών με σύγκλιση α μέτρου 9 είναι 1/6.

Prime numbers (highlighted in red) in arithmetic progression modulo 9.

Το θεώρημα των Γκριν-Τάο δείχνει ότι υπάρχουν αυθαίρετα μεγάλες αριθμητικές πρόοδοι που περιέχουν πρώτους αριθμούς. Ένας περιττός πρώτος αριθμός p εκφράζεται ως το άθροισμα δύο τετραγώνων, p = x² + y², ακριβώς αν ο p συγκλίνει στο 1 με μέτρο 4.

Τιμές πρώτων αριθμών δευτεροβάθμιων πολυωνύμων

The Ulam spiral. Red pixels show prime numbers. Primes of the form 4n² − 2n + 41 are highlighted in blue.

Ο Όιλερ σημείωσε ότι η συνάρτηση

n² + n + 41

δίνει πρώτους αριθμούς για 0 ≤ n < 40, ένα γεγονός που οδηγεί βαθιά μέσα στην αλγεβρική θεωρία αριθμών και πιο συγκεκριμένα στους αριθμούς Χέεγκνερ. Για μεγαλύτερα n, η συνάρτηση δίνει σύνθετους αριθμούς. Η εικασία F των Χάρντι-Λίτλγουντ κάνει μια ασυμπτωτική πρόβλεψη για την πυκνότητα των πρώτων αριθμών μεταξύ των τιμών των δευτεροβάθμιων πολυωνύμων (με ακέραιους συντελεστές a, b και c)

$f(n)=ax^{2}+bx+c\,$

Ωστόσο, η πρόοδος έχει αποδειχτεί δύσκολο να βρεθεί: κανένα δευτεροβάθμιο πολυώνυμο (με a ≠ 0) δεν είναι γνωστό να παίρνει απείρως πολλούς πρώτους αριθμούς ως τιμές. Η σπείρα του Ούλαμ απεικονίζει όλους τους φυσικούς αριθμούς με ένα σπειροειδές τρόπο. Οι πρώτοι αριθμοί μαζεύονται σε συγκεκριμένες διαγώνιες και όχι σε άλλες, γεγονός που υποδηλώνει ότι κάποια δευτεροβάθμια πολυώνυμα παίρνουν ως τιμές πρώτους αριθμούς πιο συχνά από άλλα.

Ανοικτά ερωτήματα

Η συνάρτηση ζήτα και η υπόθεση του Ρίμαν

Το σχέδιο της συνάρτησης ζήτα ζ(s). Στο s=1, η συνάρτηση έχει ένα πόλο, ο οποίος όπως λέμε τείνει στο άπειρο.

Η συνάρτηση ζήτα του Ρίμαν ζ(s) ορίζεται ως ένα άπειρο άθροισμα

$\zeta (s)=\sum _{n=1}^{\infty }{\frac {1}{n^{s}}},$

όπου s είναι ένας μιγαδικός αριθμός με πραγματικό μέρος μεγαλύτερο του 1. Είναι συνέπεια του θεμελιώδους θεωρήματος της αριθμητικής ότι αυτό το άθροισμα συμφωνεί με το άπειρο γινόμενο

$\prod _{p{\text{ prime}}}{\frac {1}{1-p^{-s}}}.$

Η συνάρτηση ζήτα είναι στενά συνδεδεμένη με τους πρώτους αριθμούς. Για παράδειγμα, το προαναφερθέν γεγονός ότι υπάρχουν άπειροι πρώτοι αριθμοί μπορεί επίσης να δειχθεί χρησιμοποιώντας τη συνάρτηση ζήτα: αν υπήρχαν πεπερασμένου του πλήθους πρώτοι αριθμοί, τότε η ζ(1) θα είχε μια πεπερασμένη τιμή. Ωστόσο, η αρμονική σειρά 1 + 1/2 + 1/3 + 1/4 + ... αποκλίνει (δηλαδή ξεπερνά κάθε δεδομένο αριθμό) κι έτσι πρέπει να υπάρχουν απείρως πολλοί πρώτοι αριθμοί. Ένα άλλο παράδειγμα της σημαντικότητας της συνάρτησης ζήτα και μια γεύση από τη σύγχρονη αλγεβρική θεωρία αριθμών είναι η παρακάτω ταυτότητα (πρόβλημα της Βασιλείας), σύμφωνα με τον Όιλερ,

$\zeta (2)=\prod _{p}{\frac {1}{1-p^{-2}}}={\frac {\pi ^{2}}{6}}.$

Η τιμή της ζ(2), 6/π², είναι η πιθανότητα δύο τυχαία επιλεγμένοι αριθμοί να είναι σχετικά πρώτοι.

Η χωρίς απόδειξη υπόθεση του Ρίμαν, από το 1859, αναφέρει ότι εκτός από τους s = -2, -4, ... όλα τα μηδενικά της ζήτα συνάρτησης έχουν πραγματικό μέρος ίσο με 1/2. Η σύνδεση στους πρώτους αριθμούς είναι αυτή που ουσιαστικά λέει ότι οι πρώτοι αριθμοί κατανέμονται όσο πιο τακτικά γίνεται. Από φυσική άποψη, η υπόθεση περίπου αναφέρει ότι η αταξία στην κατανομή των πρώτων αριθμών προέρχεται μόνο από τυχαίο θόρυβο. Από μαθηματική άποψη, η υπόθεση περίπου αναφέρει ότι η ασυμπτωτική κατανομή των πρώτων αριθμών (σχετικά με το ότι οι αριθμοί x/logx που είναι μικρότεροι από x είναι πρώτοι αριθμοί, θεώρημα πρώτων αριθμών) επίσης ισχύει για πολύ μικρότερα σε μήκος διαστήματα σχετικά με την τετραγωνική ρίζα του x (για διαστήματα κοντά στο x). Αυτή η υπόθεση θεωρείται γενικά ορθή. Πιο συγκεκριμένα, η απλούστερη υπόθεση είναι ότι οι πρώτοι αριθμοί δε θα έπρεπε να έχουν σημαντικές αταξίες χωρίς ένα καλό λόγο.

Άλλες εικασίες

Εκτός από την υπόθεση του Ρίμαν, πολλές ακόμη εικασίες σχετικά με τους πρώτους αριθμούς έχουν διατυπωθεί. Συχνά έχοντας μια στοιχειώδη σύνθεση, πολλές από αυτές τις εικασίες δεν έχουν απόδειξη για δεκαετίες: και τα τέσσερα προβλήματα του Λαντό παραμένουν άλυτα από το 1912. Ένα από αυτά είναι η εικασία του Γκόλντμπαχ, η οποία βεβαιώνει ότι κάθε άρτιος ακέραιος αριθμός n μεγαλύτερος του 2 μπορεί να γραφεί ως άθροισμα δύο πρώτων αριθμών. Από το Φεβρουάριο του 2011, αυτή η εικασία έχει επαληθευτεί για όλους τους αριθμούς μέχρι και n = 2 · 10¹⁷. Πιο απλές προτάσεις από αυτή έχουν αποδειχτεί, για παράδειγμα το θεώρημα του Βινογκραντόφ λέει ότι κάθε αρκετά μεγάλος περιττός ακέραιος αριθμός μπορεί να γραφεί ως άθροισμα τριών πρώτων αριθμών. Το θεώρημα του Κεν λέει ότι κάθε αρκετά μεγάλος άρτιος αριθμός μπορεί να γραφεί ως άθροισμα ενός πρώτου και ενός ημιπρώτου (= γινόμενο δύο πρώτων αριθμών) αριθμού. Επιπρόσθετα, κάθε άρτιος ακέραιος αριθμός μπορεί να γραφεί ως άθροισμα έξι πρώτων αριθμών. Το τμήμα της θεωρίας αριθμών που μελετά αυτές τις ερωτήσεις ονομάζεται πρόσθετη θεωρία αριθμών.

Άλλες εικασίες που έχουν σχέση με την ερώτηση αν ένα άπειρο σύνολο πρώτων αριθμών που υπόκειται σε κάποιους περιορισμούς υπάρχει. Εικάζεται ότι υπάρχουν άπειροι το πλήθος πρώτοι Φιμπονάτσι και άπειροι το πλήθος πρώτοι Μερσέν αριθμοί, αλλά όχι άπειροι πρώτοι Φερμά αριθμοί. Δεν είναι γνωστό αν υπάρχουν ή όχι άπειροι το πλήθος πρώτοι Βίφεριχ αριθμοί και άπειροι το πλήθος ευκλείδειοι πρώτοι αριθμοί.

Ένας τρίτος τύπος εικασιών αφορά τις πτυχές της κατανομής των πρώτων αριθμών. Εικάζεται ότι υπάρχουν απείρως πολλοί δίδυμοι πρώτοι αριθμοί, ζευγάρια πρώτων αριθμών με διαφορά 2 (εικασία των διδύμων πρώτων αριθμών). Η εικασία του Πόλινακ ενισχύει την παραπάνω εικασία, καθώς αναφέρει ότι για κάθε θετικό ακέραιο αριθμό n, υπάρχουν απείρως πολλά ζευγάρια διαδοχικών πρώτων αριθμών με διαφορά 2n. Εικάζεται ότι υπάρχουν απείρως πολλοί πρώτοι αριθμοί της μορφής n² + 1. Αυτές οι εικασίες είναι ειδικές περιπτώσεις της ευρείας υπόθεσης Η του Σίντσελ. Η εικασία του Μπρόκαρντ λέει ότι υπάρχουν πάντα τουλάχιστον τέσσερις πρώτοι αριθμοί μεταξύ των τετραγώνων δύο διαδοχικών πρώτων αριθμών μεγαλύτερων του 2. Η εικασία του Λεγκρέντ αναφέρει ότι υπάρχει ένας πρώτος αριθμός μεταξύ n² και (n + 1)² για κάθε θετικό ακέραιο αριθμό n. Υπονοείται από την ισχυρότερη εικασία του Κράμερ.

Επιπλέον, ένα από τα ανοιχτά ερωτήματα της σύγχρονης θεωρίας αριθμών είναι το πρόβλημα της παραγοντοποίησης μεγάλων ακεραίων, δηλαδή της εύρεσης αλγορίθμου παραγοντοποίησης σε πολυωνυμικό χρόνο. Στην σκιά αυτού του προβλήματος αναπτύχθηκε η Κρυπτογράφηση Δημόσιου Κλειδιού και ειδικότερα του κρυπτοσυστήματος RSA.

Οι εικασίες του Γκόλντμπαχ

Είναι πολύ γνωστή η πρώτη εικασία που διατύπωσε ο Κρίστιαν Γκόλντμπαχ 1690-1764, η οποία σχετίζεται με τους πρώτους αριθμούς. Ο Γκόλντμπαχ υποστήριξε ότι κάθε άρτιος αριθμός μεγαλύτερος του 2, μπορεί να γραφεί ως άθροισμα δύο πρώτων αριθμών. Η απόδειξη της παραπάνω εικασίας ταλανίζει ακόμα και σήμερα τους μαθηματικούς, καθώς παράλληλα οι υπολογιστές επιβεβαιώνουν την εικασία για όλο και μεγαλύτερους αριθμούς. Το 1998, η εικασία επιβεβαιώθηκε για αριθμούς μέχρις και της τάξης του $10^{14}$

Η δεύτερη εικασία του Γκόλντμπαχ έγκειται στο ότι κάθε περιττός αριθμός του 6 είναι άθροισμα τριών πρώτων αριθμών. Και αυτή η εικασία παραμένει αναπόδεικτη, αν και επιβεβαιώνεται από ηλεκτρονικούς υπολογιστές. Τυχόν απόδειξη της πρώτης εικασίας του Γκόλντμπαχ θα αποδείκνυε αμέσως και τη δεύτερη εικασία.

Εφαρμογές

Για πολύ καιρό, η θεωρία αριθμών γενικά και η μελέτη των πρώτων αριθμών συγκεκριμένα αποτελούσαν κλασικό παράδειγμα των καθαρών μαθηματικών, με καθόλου εφαρμογές έξω από το θεωρητικό κομμάτι. Πιο συγκεκριμένα, μαθηματικοί που ασχολήθηκαν με τη θεωρία αριθμών, όπως ο Βρετανός Γ. Χ. Χάρντι υπερηφανεύονταν ότι εργάζονταν πάνω σε κάτι που δεν είχε καμία στρατιωτική σημασία. Ωστόσο, αυτή η οπτική καταρρίφθηκε τη δεκαετία του 1970, όταν ανακοινώθηκε δημοσίως ότι οι πρώτοι αριθμοί μπορούσαν να χρησιμοποιηθούν ως βάση για τη δημιουργία αλγορίθμων κρυπτογραφίας δημοσίου κλειδιού. Οι πρώτοι αριθμοί επίσης χρησιμοποιήθηκαν για πίνακες κατακερματισμού και για γεννήτριες ψευδοτυχαίων αριθμών.

Μερικές μηχανές με στροφείο (rotor machines) σχεδιάστηκαν με ένα διαφορετικό πλήθος καρφιών σε κάθε στροφείο, με το πλήθος των καρφιών σε κάθε στροφείο να είτε πρώτος, ή σύνθετος στο πλήθος των καρφιών οποιουδήποτε άλλου στροφείου. Αυτό βοήθησε στη δημιουργία ενός πλήρους κύκλου πιθανών θέσεων στροφείων πριν την επανάληψη κάθε θέσης.

Ο Διεθνής Πρότυπος Αριθμός Βιβλίου δουλεύει με ένα ψηφίο ελέγχου, το οποίο εκμεταλλεύεται το γεγονός ότι ο αριθμός 11 είναι πρώτος αριθμός.

Αριθμητική modular ενός πρώτου αριθμού και πεπερασμένα σώματα

Η αριθμητική modular τροποποιεί τη συνήθη αριθμητική χρησιμοποιώντας μόνο τους αριθμούς

{0, 1, 2, ..., n - 1},

όπου ο n είναι ένας σταθερός φυσικός αριθμός που ονομάζεται modulus. ο υπολογισμός των αθροισμάτων, των διαφορών και των γινομένων γίνεται ως συνήθως, αλλά όποτε συναντούμε ένα αρνητικό αριθμό ή ένα αριθμό μεγαλύτερο του n - 1, αυτός αντικαθίσταται από το υπόλοιπο μετά τη διαίρεση από τον n. Για παράδειγμα, για n = 7, το άθροισμα 3 + 5 ισούται με 1 αντί για 8, αφού όταν το 8 διαιρείται με το 7 αφήνει υπόλοιπο 1. Για να αναφερθούμε σε αυτό, λέμε ότι το 3 + 5 είναι σύμφωνο με το 1 modulo 7 και γράφουμε

$3+5\equiv 1{\pmod {7}}.$

Ομοίως, 6 + 1 ≡ 0 (mod 7), 2 - 5 ≡ 4 (mod 7), αφού -3 + 7 = 4 και 3 · 4 ≡ 5 (mod 7), καθώς το 12 αφήνει υπόλοιπο το 5. Οι βασικές ιδιότητες της πρόσθεσης και του πολλαπλασιασμού γνωστές από τους ακεραίους ισχύουν και στην modular αριθμητική. Στον τομέα της αφηρημένης άλγεβρας, το παραπάνω σύνολο των ακεραίων, το οποίο συμβολίζεται με Z/nZ, είναι επομένως ένας αντιμεταθετικός δακτύλιος για κάθε n. Η διαίρεση όμως, δεν είναι γενικά δυνατή σε αυτή την κατάσταση. Για παράδειγμα, για n = 6, στην εξίσωση

$3\cdot x\equiv 2{\pmod {6}},$

μια λύση του x, η οποία θα ήταν ανάλογη με 2/3, δεν μπορεί να βρεθεί, καθώς το ένα μπορεί να βρεθεί υπολογίζοντας 3 · 0, ..., 3 · 5 modulo 6. Το ιδιαίτερο χαρακτηριστικό των πρώτων αριθμών είναι το εξής: η διαίρεση είναι δυνατή στη modular αριθμητική αν και μόνο αν ο n είναι πρώτος αριθμός. Ισοδύναμα, ο n είναι πρώτος αριθμός αν και μόνο αν όλοι οι ακέραιοι m που ικανοποιούν την ανισότητα 2 ≤ m ≤ n − 1 είναι σχετικοί πρώτοι με τον n, δηλαδή ο μόνος κοινός διαιρέτης τους είναι το 1. Πράγματι, για n = 7, η εξίσωση

$3\cdot x\equiv 2\ \ (\operatorname {mod} \ 7),$

έχει μοναδική λύση, τη x = 3. Εξαιτίας αυτού, για κάθε πρώτο αριθμό p, το Z/pZ (μερικές φορές σημειώνεται ως F_p) ονομάζεται σώμα ή πιο συγκεκριμένα πεπερασμένο σώμα, αφού περιέχει πεπερασμένου του πλήθους, δηλαδή p, στοιχεία. Ένα πλήθος θεωρημάτων μπορούν να προέρχονται από τη μελέτη του F_p με αυτό τον αφηρημένο τρόπο. Για παράδειγμα, το μικρό θεώρημα του Φερμά, το οποίο αναφέρει ότι

$a^{p-1}\equiv 1(\operatorname {mod} \ p)$

για κάθε ακέραιο αριθμό a που δε διαιρείται από τον p, μπορεί να αποδειχθεί χρησιμοποιώντας αυτές τις έννοιες. Αυτό συνεπάγεται ότι

$\sum _{a=1}^{p-1}a^{p-1}\equiv (p-1)\cdot 1\equiv -1{\pmod {p}}.$

Η εικασία του Τζιούγκα λέει ότι αυτή η εξίσωση είναι επίσης μια επαρκής συνθήκη για να πούμε ότι ο p είναι πρώτος αριθμός. Μια άλλη συνέπεια του μικρού θεωρήματος του Φερμά είναι η εξής: αν ο p είναι ένας πρώτος αριθμός διαφορετικός του 2 και του 5, ο 1/p είναι πάντα ένας περιοδικός αριθμός, με περίοδο p - 1 ή ένα διαιρέτη του p - 1. Το κλάσμα 1/p εκφρασμένο επίσης στη βάση q (αντί στη βάση 10) έχει παρόμοιο αποτέλεσμα, υπό τον όρο ο p δεν είναι παράγοντας του q ως πρώτος αριθμός. Το θεώρημα του Ουίλσον λέει ότι ένας ακέραιος αριθμός p > 1 είναι πρώτος αν και μόνο αν το παραγοντικό (p - 1)! + 1 διαιρείται από τον p. Επιπλέον, ένας ακέραιος αριθμός n > 4 είναι σύνθετος αν και μόνο αν (n - 1)! είναι διαιρέσιμο από τον n.

Άλλες μαθηματικές συμβολές των πρώτων αριθμών

Πολλά μαθηματικά πεδία χρησιμοποιούν πολύ τους πρώτους αριθμούς. Ένα παράδειγμα από τη θεωρία των πεπερασμένων σωμάτων είναι τα θεωρήματα του Sylow: αν G είναι ένα πεπερασμένο σώμα και pⁿ είναι η μεγαλύτερη δύναμη του πρώτου αριθμού p που διαιρεί τη διάταξη G, τότε η G έχει μια υποομάδα τάξης pⁿ. Επίσης, κάθε ομάδα με διάταξη πρώτων αριθμών είναι κυκλική (θεώρημα του Lagrange).

Κρυπτογράφηση δημόσιου κλειδιού

Αρκετοί αλγόριθμοι κρυπτογράφησης δημόσιου κλειδιού, όπως ο RSA και το πρωτόκολλο ανταλλαγής κλειδιών των Ντίφι-Χέλμαν, βασίζονται στους μεγάλους πρώτους αριθμούς (για παράδειγμα πρώτοι αριθμοί μεγέθους 512 bit χρησιμοποιούνται συχνά για τον RSA και πρώτοι αριθμοί μεγέθους 1024 bit είναι συνήθεις για τον αλγόριθμο Ντίφι–Χέλμαν.). Ο RSA βασίζεται στην υπόθεση ότι είναι πολύ πιο εύκολο (δηλαδή πιο αποτελεσματικό) να εκτελέσουμε πολλαπλασιασμό δύο (μεγάλων) αριθμών x και y από το να υπολογίσουμε τους x και y (υποτίθεται ότι είναι σχετικά πρώτοι) αν μόνο το γινόμενο xy είναι γνωστό. Η ανταλλαγή κλειδιών των Ντίφι-Χέλμαν βασίζεται στο γεγονός ότι υπάρχουν αποτελεσματικοί αλγόριθμοι για modular ύψωση σε δύναμη, ενώ η αντίστροφη λειτουργία του διακριτού λογαρίθμου υποτίθεται ότι είναι ένα δύσκολο πρόβλημα.

Οι πρώτοι αριθμοί στη φύση

Αναπόφευκτα, μερικοί από τους αριθμούς που συναντώνται στη φύση είναι πρώτοι. Ωστόσο, υπάρχουν σχετικά λίγα παραδείγματα αριθμών, οι οποίοι εμφανίζονται στη φύση, επειδή είναι πρώτοι.

Ένα παράδειγμα της χρήσης των πρώτων αριθμών στη φύση είναι ως εξελικτική στρατηγική που χρησιμοποιείται από τα τζιτζίκια του γένους Magicicada. Αυτά τα έντομα περνούν τον περισσότερο χρόνο της ζωής τους ως προνύμφες υπογείως. Τα έντομα αυτά μεγαλώνουν και στη συνέχεια βγαίνουν από τις φωλιές τους μετά από 13 ή 17 χρόνια, χρονικό σημείο από το οποίο θα αρχίσουν να πετάνε, να γεννάνε και μετά από λίγες εβδομάδες το πολύ πεθαίνουν. Θεωρείται ότι η λογική για αυτό είναι ότι τα διαστήματα πρώτων αριθμών μεταξύ καταστάσεων έκτακτης ανάγκης καθιστούν πολύ δύσκολο να εξελιχθούν τα αρπακτικά, οι οποίοι θα μπορούσαν να εξειδικευτούν ως θηρευτές των Magicicada. Αν τα έντομα αυτά δεν εμφανίζονταν σε διαστήματα πρώτων αριθμών, ας πούμε κάθε 12 χρόνια, τότε οι θηρευτές τους που θα εμφανίζονταν κάθε 2, 3, 4, 6 ή 12 χρόνια θα ήταν σίγουρο ότι θα τα συναντούσαν. Για πάνω από 200 χρόνια, ο μέσος όρος του πληθυσμού των αρπακτικών κατά τη διάρκεια της πιθανής γέννησης 14 και 15 ετών των τζιτζικιών θα ήταν έως και 2% υψηλότερα από ότι κατά τη διάρκεια γέννησής τους 13 και 17 ετών. Παρόλο που είναι μικρό, το πλεονέκτημα αυτό εμφανίζεται να είναι αρκετό για να οδηγηθούν στη φυσική επιλογή υπέρ της προνομιακής αρίθμησης του κύκλου ζωής για αυτά τα έντομα.

Αυτό είναι το πρόβλημα ότι τα μηδενικά της συνάρτηση ζήτα ζήτα συνάρτησης είναι συνδεδεμένα με τα επίπεδα ενέργειας των πολύπλοκων κβαντικών συστημάτων.

Γενικεύσεις

Η έννοια του πρώτου αριθμού είναι τόσο σημαντική που έχει γενικευτεί με διάφορους τρόπους σε ποικίλους τομείς των μαθηματικών. Γενικά, ο όρος πρώτος προσδιορίζει την ελαχιστοποίηση ή το διαχωρισμό ενός αντικειμένου στα βασικά του στοιχεία. Για παράδειγμα, το πεδίο των πρώτων αριθμών είναι το μικρότερο υποδιάστημα ενός διαστήματος F που περιέχει το 0 και το 1. Είναι είτε το σύνολο Q ή το πεπερασμένο σύνολο με p στοιχεία, εξ ου και η ονομασία. Συχνά ένας δεύτερος, πρόσθετος ορισμός προορίζεται από τη χρήση της λέξης πρώτος, δηλαδή ότι κάθε αντικείμενο μπορεί ουσιαστικά και μοναδικά να αναλυθεί στα βασικά χαρακτηριστικά του. Για παράδειγμα, στη θεωρία των κόμπων, ένας πρώτος (βασικός) κόμπος είναι ένας κόμπος, ο οποίος είναι αδιάσπαστος, με την έννοια ότι δεν μπορεί να γραφεί ως άθροισμα δύο τετριμμένων κόμπων. Κάθε κόμπος μπορεί να εκφραστεί μοναδικά ως ένα συνδεδεμένο άθροισμα βασικών (πρώτων) κόμπων. Άλλα παραδείγματα αυτού του τύπου είναι τα μοντέλα πρώτων αριθμών και οι πρώτοι αριθμοί τριπλής πολλαπλότητας.

Πρώτα στοιχεία στους δακτύλιους

Από τους πρώτους αριθμούς προκύπτουν δύο πιο γενικές έννοιες, οι οποίες εφαρμόζονται στα στοιχεία κάθε αντιμεταθετικού δακτυλίου R, μια αλγεβρική δομή, όπου ορίζονται η πρόσθεση, η αφαίρεση και ο πολλαπλασιασμός: πρώτα στοιχεία και στοιχεία που δεν ανάγονται. Ένα στοιχείο p του R ονομάζεται πρώτο στοιχείο αν δεν είναι ούτε μηδέν ούτε μονάδα (δηλαδή δεν έχει αντίστροφο στον πολλαπλασιασμό) και ικανοποιεί την παρακάτω προϋπόθεση: δοθέντων x και y στο R, τέτοια ώστε ο p να διαιρεί το γινόμενο xy, τότε ο p διαιρεί τον x ή τον y. Ένα στοιχείο δεν ανάγεται αν δεν μπορεί να γραφεί ως γινόμενο δύο στοιχείων του δακτυλίου, τα οποία δεν είναι μονάδες. Στο δακτύλιο Ζ των ακεραίων αριθμών, το σύνολο των πρώτων στοιχείων ισούται με το σύνολο των στοιχείων που δεν ανάγονται, το οποίο είναι το

$\{\dots ,-11,-7,-5,-3,-2,2,3,5,7,11,\dots \}\,.$

Σε κάθε δακτύλιο R, κάθε πρώτο στοιχείο δεν ανάγεται. Το αντίστροφο γενικά δεν ισχύει, αλλά ισχύει για τη μοναδική παραγοντοποίηση διαστημάτων.

Το θεμελιώδες θεώρημα της αριθμητικής συνεχίζει να ισχύει στη μοναδική παραγοντοποίηση διαστημάτων. Ένα παράδειγμα τέτοιου διαστήματος είναι οι ακέραιοι του Γκάους Z[i], οι οποίοι αποτελούν το σύνολο των μιγαδικών αριθμών της μορφής a + bi, όπου το i δηλώνει τη μονάδα των φανταστικών αριθμών και οι a και b είναι τυχαίοι ακέραιοι αριθμοί. Τα πρώτα στοιχεία του συνόλου αυτού είναι γνωστά ως πρώτοι αριθμοί του Gauss. Κάθε πρώτος αριθμός (ακέραιος) δεν είναι πρώτος αριθμός του Γκάους: στο μεγαλύτερο δακτύλιο Z[i], 2 παράγοντες στο γινόμενο των δύο πρώτων αριθμών του Γκάους (1 + i) και (1 - i). Λογικοί πρώτοι αριθμοί (δηλαδή πρώτα στοιχεία του Ζ) της μορφής 4k + 3 είναι πρώτοι αριθμοί του Γκάους, ενώ όλοι οι πρώτοι αριθμοί της μορφής 4k + 1 δεν είναι.

Ιδεώδη πρώτων αριθμών

Στη θεωρία των δακτυλίων, η έννοια του αριθμού αντικαθίσταται γενικά από την έννοια του ιδεώδους. Τα ιδεώδη των πρώτων αριθμών, τα οποία γενικεύουν τα πρώτα στοιχεία, υπό την έννοια ότι το βασικό ιδανικό που παράγεται από ένα πρώτο στοιχείο είναι ιδανικό πρώτου αριθμού, είναι ένα σημαντικό εργαλείο και αντικείμενο της μελέτης της αντιμεταθετικής άλγεβρας, της αλγεβρικής θεωρίας αριθμών και της αλγεβρικής γεωμετρίας. Τα ιδανικά των πρώτων αριθμών του δακτυλίου των ακεραίων αριθμών είναι τα ιδανικά (0), (2), (3), (5), (7), (11), ... Το θεμελιώδες θεώρημα της αριθμητικής γενικεύεται στο θεώρημα των Λάσκερ–Νόθερ, το οποίο εκφράζει κάθε ιδανικό σε ένα αντιμεταθετικό δακτύλιο του Noether ως την τομή βασικών ιδανικών, τα οποία αποτελούν τις κατάλληλες γενικεύσεις των δυνάμεων των πρώτων αριθμών.

Τα ιδανικά των πρώτων αριθμών είναι τα σημεία των αλγεβρογεωμετρικών αντικειμένων, μέσω της έννοιας του φάσματος ενός δακτυλίου. Η αλγεβρική γεωμετρία επίσης επωφελείται από αυτή την έννοια και πράγματι πολλές έννοιες υπάρχον ταυτόχρονα και στη γεωμετρία και στη θεωρία αριθμών. Για παράδειγμα, η παραγοντοποίηση ή η διακλάδωση των ιδανικών των πρώτων αριθμών, όταν αρθεί σε ένα επεκταμένο διάστημα, ένα βασικό πρόβλημα της αλγεβρικής θεωρίας αριθμών, έχει κάποιες ομοιότητες με διακλάδωση στη γεωμετρία. Τέτοιες ερωτήσεις διακλάδωσης, οι οποίες εμφανίζονται ακόμη και σε ερωτήσεις της θεωρίας αριθμών, αποκλειστικά ασχολούνται με ακεραίους αριθμούς. Για παράδειγμα, τα ιδανικά των πρώτων αριθμών στο δακτύλιο των ακεραίων αριθμών σε διάστημα με τα τετράγωνα των αριθμών μπορούν να χρησιμοποιηθούν στην απόδειξη της τετραγωνικής αμοιβαιότητας, μια πρόταση η οποία αφορά τη λύση των δευτεροβάθμιων εξισώσεων

$x^{2}\equiv p\ \ ({\text{mod }}q),\,$

όπου ο x είναι ένας ακέραιος και p και q είναι (συνήθεις) πρώτοι αριθμοί. Οι πρόσφατες προσπάθειες για την απόδειξη του τελευταίου θεωρήματος του Φερμά κορυφώθηκαν, όταν ο Kummer εισήγαγε τους τακτικούς πρώτους αριθμούς, δηλαδή πρώτους αριθμούς που ικανοποιούν μια συγκεκριμένη προϋπόθεση σχετικά με την αποτυχία της μοναδικής παραγοντοποίησης στο δακτύλιο που αποτελείται από τις εκφράσεις

$a_{0}+a_{1}\zeta +\cdots +a_{p-1}\zeta ^{p-1}\,,$

όπου a₀, ..., a_p-1 είναι ακέραιοι και ο ζ είναι ένας μιγαδικός αριθμός, τέτοιος ώστε ζ^p = 1.

Αποτιμήσεις

Η θεωρία των αποτιμήσεων (valuation theory) μελετά συγκεκριμένες συναρτήσεις από ένα διάστημα Κ στους πραγματικούς αριθμούς R που ονομάζονται αποτιμήσεις. Κάθε τέτοια αποτίμηση αποδίδει μια τοπολογία στο Κ και δυο αποτιμήσεις ονομάζονται ισοδύναμες, αν αποδίδουν την ίδια τοπολογία. Ένας πρώτος αριθμός του Κ (μερικές φορές λέγεται μια τοποθεσία του Κ) είναι μια κλάση ισοδυναμίας των αποτιμήσεων. Για παράδειγμα, η p-αδική αποτίμηση ενός ρητού αριθμού q ορίζεται να είναι ο ακέραιος v_p(q), τέτοιος ώστε

$q=p^{v_{p}(q)}{\frac {r}{s}},$

όπου οι r και s δεν είναι διαιρέσιμοι από τον p. Για παράδειγμα, v₃(18/7) = 2. Ο p-αδικός τύπος ορίζεται ως

$\left|q\right|_{p}:=p^{-v_{p}(q)}.\,$

Πιο συγκεκριμένα, αυτός ο τύπος γίνεται μικρότερος, όταν ένας αριθμός πολλαπλασιάζεται από τον p, σε έντονη αντίθεση με τη συνήθη απόλυτη τιμή (επίσης αναφέρεται και ως άπειρος πρώτος). Ενώ συμπληρώνουμε τον Q (περίπου συμπληρώνοντας τα κενά) όσον αφορά την απόλυτη τιμή, αυτή αποδίδει το διάστημα των πραγματικών αριθμών, συμπληρώνοντας όσον αφορά τον p-αδικό τύπο |-|_p αποδίδει το διάστημα των p-αδικών αριθμών. Αυτοί είναι ουσιαστικά όλοι οι πιθανοί τρόποι να συμπληρώσουμε τον Q, σύμφωνα με το θεώρημα του Οστρόφσκι.Ορισμένες αριθμητικές ερωτήσεις που σχετίζονται με τον Q ή με πιο γενικά καθολικά πεδία μπορούν να μεταφερθούν εμπρός και πίσω στα συμπληρωμένα (ή τοπικά) διαστήματα. Αυτή η τοπική-καθολική αρχή υπογραμμίζει ξανά τη σημασία των πρώτων αριθμών στη θεωρία αριθμών.

Στις τέχνες και τη λογοτεχνία

Οι πρώτοι αριθμοί έχουν επηρεάσει πολλούς καλλιτέχνες και συγγραφείς. Ο Γάλλος συνθέτης Ολιβιέρ Μεσσιάν χρησιμοποίησε τους πρώτους αριθμούς για να δημιουργήσει αμετρική μουσική μέσω φυσικών φαινομένων. Σε έργα, όπως Λα Νατιβίτ ντου Σενό (1935) και Κουάτρ ετούντ ντε ριμ (1949–50), ο συνθέτης χρησιμοποιεί ταυτόχρονα μοτίβα με μήκη που δίνονται από διαφορετικούς πρώτους αριθμούς για να δημιουργήσει απρόβλεπτους ρυθμούς: οι πρώτοι αριθμοί 41, 43, 47 και 53 εμφανίζονταi στο έργο "Neumes rythmiques". Σύμφωνα με τον Μεσσιάν, αυτός ο τρόπος σύνθεσης ήταν εμπνευσμένος από τις κινήσεις της φύσης, τις κινήσεις της ελεύθερης και άνισης διάρκειας.

Στο επιστημονικής φαντασίας μυθιστόρημά του Contact, ο επιστήμονας της NASA Καρλ Σάγκαν αναφέρει ότι οι πρώτοι αριθμοί μπορούν να χρησιμοποιηθούν ως ένα μέσο επικοινωνίας με τους εξωγήινους, μια ιδέα που πρώτα ανέπτυξε ανεπίσημα με τον Αμερικανό αστρονόμο Φρανκ Ντράκε το 1975. Στο μυθιστόρημά του The Curious Incident of the Dog in the Night-Time ο Μαρκ Χάντον, ο αφηγητής οργανώνει τα τμήματα της ιστορίας από διαδοχικούς πρώτους αριθμούς.

Πολλές ταινίες, όπως Cube, Sneakers, The Mirror Has Two Faces και A Beautiful Mind αντικατοπτρίζουν μια δημοφιλή γοητεία των πρώτων αριθμών και της κρυπτογραφίας. Οι πρώτοι αριθμοί χρησιμοποιούνται ως αλληγορία για τη μοναξιά και την απομόνωση στο μυθιστόρημα του The Solitude of Prime Numbers του Paolo Giordano, στο οποίο οι πρώτοι αριθμοί παρουσιάζονται ως ξένοι μεταξύ των ακεραίων αριθμών.

Δείτε ακόμη

• Θεώρημα πρώτων αριθμών
• Αναζήτηση μεγάλων πρώτων αριθμών

Περαιτέρω ανάγνωση

Ελληνική βιβλιογραφία

• Λάκκης, Κωνσταντίνος (1991). Θεωρία Αριθμών (7η έκδοση). Ζήτη. 
• Αντωνιάδης, Ι.· Κοντογεώργης, Α. (2015). Θεωρία αριθμών και εφαρμογές. Κάλλιπος, Ανοικτές Ακαδημαϊκές Εκδόσεις. 
• Πουλάκης, Δ. (2015). Υπολογιστική θεωρία αριθμών. Κάλλιπος, Ανοικτές Ακαδημαϊκές Εκδόσεις. doi:10.57713/kallipos-323. 
• Κολουντζάκης, Μ.· Παπαχριστόδουλος, Χ. (2015). «Θεωρία Αριθμών». Διακριτά μαθηματικά. Κάλλιπος, Ανοικτές Ακαδημαϊκές Εκδόσεις. 

Ξένη βιβλιογραφία

• Apostol, Thomas M. (1976), Introduction to Analytic Number Theory, New York: Springer, ISBN 0-387-90163-9, https://archive.org/details/introductiontoan00apos_0 
• Conway, John Horton; Guy, Richard K. (1996), The Book of Numbers, New York: Copernicus, ISBN 978-0-387-97993-9 
• Crandall, Richard; Pomerance, Carl (2005), Prime Numbers: A Computational Perspective (2nd έκδοση), Berlin, New York: Springer-Verlag, ISBN 978-0-387-25282-7 
• Derbyshire, John (2003), Prime obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, https://archive.org/details/primeobsessionbe00derb_0 
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94268-1 
• Furstenberg, Harry (1955), «On the infinitude of primes», The American Mathematical Monthly (Mathematical Association of America) 62 (5): 353, doi:10.2307/2307043, ISSN 0002-9890 
• Green, Ben; Tao, Terence (2008), «The primes contain arbitrarily long arithmetic progressions», Annals of Mathematics 167 (2): 481–547, doi:10.4007/annals.2008.167.481 
• Gowers, Timothy (2002), Mathematics: A Very Short Introduction, en:Oxford University Press, ISBN 978-0-19-285361-5 
• Guy, Richard K. (1981), Unsolved Problems in Number Theory, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90593-8 
• Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5 
• Hardy, Godfrey Harold (1908), A Course of Pure Mathematics, en:Cambridge University Press, ISBN 978-0-521-09227-2 
• Hardy, Godfrey Harold (1940), A Mathematician's Apology, Cambridge University Press, ISBN 978-0-521-42706-7 
• Hill, Peter Jensen, επιμ.. (1995), The Messiaen companion, Portland, Or: Amadeus Press, ISBN 978-0-931340-95-6 
• Hua, L. K. (2009), Additive Theory of Prime Numbers, Translations of Mathematical Monographs, 13, AMS Bookstore, ISBN 978-0-8218-4942-2, http://www.ams.org/bookstore-getitem/item=MMONO/13.S 
• Lehmer, D. H. (1909), Factor table for the first ten millions containing the smallest factor of every number not divisible by 2, 3, 5, or 7 between the limits 0 and 10017000, Washington, D.C.: Carnegie Institution of Washington 
• Narkiewicz, Wladyslaw (2000), The development of prime number theory: from Euclid to Hardy and Littlewood, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-66289-1 
• Ribenboim, Paulo (2004), The little book of bigger primes, Berlin, New York: Springer-Verlag, ISBN 978-0-387-20169-6 
• Riesel, Hans (1994), Prime numbers and computer methods for factorization, Basel, Switzerland: Birkhäuser, ISBN 978-0-8176-3743-9 
• Sabbagh, Karl (2003), The Riemann hypothesis, Farrar, Straus and Giroux, New York, ISBN 978-0-374-25007-2, https://archive.org/details/riemannhypothesi00sabb 
• du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, https://archive.org/details/musicofprimessea00dusa 
• Kelly, Katherine E., επιμ.. (2001), The Cambridge companion to Tom Stoppard, Cambridge University Press, ISBN 978-0-521-64592-8 
• Stoppard, Tom (1993), Arcadia, London: Faber and Faber, ISBN 978-0-571-16934-4 

Εξωτερικοί σύνδεσμοι

• http://www.primzahlen.de/