π (μαθηματική σταθερά)
| Μέρος μιας σειράς λημμάτων για την |
| μαθηματική σταθερά π |
|---|
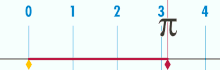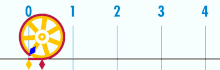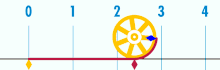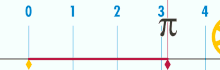 Όταν η διάμετρος του κύκλου είναι 1 η περιφέρειά του είναι ίση με π |
| Χρήσεις |
| Ιδιότητες |
| Τιμή |
| Πρόσωπα |
| Ιστορία |
| Στην κουλτούρα |
| Σχετιζόμενα θέματα |
Ο αριθμός π είναι μια μαθηματική σταθερά οριζόμενη ως ο λόγος της περιφέρειας προς τη διάμετρο ενός κύκλου ( (όπου είναι το μήκος περιφέρειας κύκλου και το μήκος διαμέτρου κύκλου), ενώ με ακρίβεια οκτώ δεκαδικών ψηφίων είναι ίσος με Εκφράζεται με το ελληνικό γράμμα π από τα μέσα του 18ου αιώνα.
Ο π είναι ένας άρρητος αριθμός, που σημαίνει ότι δεν μπορεί να εκφραστεί ακριβώς ως ο λόγος δύο ακεραίων (όπως 22/7 ή άλλα κλάσματα που χρησιμοποιούνται συνήθως για την προσέγγιση του π). Κατά συνέπεια, η δεκαδική του αναπαράσταση δεν τελειώνει ποτέ και ποτέ δεν καθίσταται μια μόνιμη και επαναλαμβανόμενη ακολουθία ψηφίων. Ο π είναι ένας υπερβατικός αριθμός, δηλαδή δεν αποτελεί ρίζα ενός μη-μηδενικού πολυωνύμου με ρητούς συντελεστές. Αυτό έχει σαν συνέπεια ότι είναι αδύνατο να λυθεί το αρχαίο πρόβλημα του τετραγωνισμού του κύκλου με κανόνα (χάρακα) και διαβήτη.
Για χιλιάδες χρόνια, μαθηματικοί προσπάθησαν να επεκτείνουν την κατανόησή τους πάνω στο π, κάποιες φορές με τον υπολογισμό της τιμής του σε υψηλό βαθμό ακρίβειας. Πριν τον 15ο αιώνα, μαθηματικοί όπως ο Αρχιμήδης και ο Λιου Χούι χρησιμοποίησαν γεωμετρικές τεχνικές βασιζόμενες σε πολύγωνα, για να υπολογίσουν την τιμή του π. Περί τον 15ο αιώνα νέοι αλγόριθμοι βασιζόμενοι σε άπειρες σειρές υπολογίζουν τον αριθμό π με μεγαλύτερη ακρίβεια και χρησιμοποιούνται από μαθηματικούς όπως ο Μαντχάβα της Σανγκαμάγκραμα, ο Ισαάκ Νιούτον, ο Λέοναρντ Όιλερ, ο Καρλ Φρίντριχ Γκάους, και ο Σρινιβάσα Ραμανούτζαν.
Τον 20ό και τον 21ο αιώνα, μαθηματικοί και πληροφορικοί ανακάλυψαν νέες μεθόδους προσέγγισης που, συνδυαζόμενοι με την αυξημένη υπολογιστική ισχύ, επέκτειναν τα γνωστά δεκαδικά ψηφία του π σε πάνω από 10 τρισεκατομμύρια 1013. Στις πιο πολλές επιστημονικές εφαρμογές δεν απαιτούνται περισσότερα από 40 ψηφία του π και έτσι το πρωταρχικό κίνητρο για αυτούς τους υπολογισμούς είναι η ανθρώπινη επιθυμία να σπάει ρεκόρ. Οι πολύπλοκοι υπολογισμοί που εμπλέκονται στον υπολογισμό των ψηφίων του π έχουν χρησιμοποιηθεί για τη δοκιμή υπερυπολογιστών, καθώς και αλγορίθμων πολλαπλασιασμού υψηλής ακρίβειας.
Το π εμφανίζεται σε πολλούς τύπους της τριγωνομετρίας και της γεωμετρίας, ειδικά όσον αφορά κύκλους, ελλείψεις ή σφαίρες. Εμφανίζεται επίσης και σε διάφορους τύπους από άλλους κλάδους της επιστήμης, όπως η κοσμολογία, η θεωρία αριθμών, η στατιστική, τα φράκταλ, η θερμοδυναμική, η μηχανική, και ο ηλεκτρομαγνητισμός. Ο καθολικός χαρακτήρας του π τον καθιστά μια από τις πιο ευρέως γνωστές μαθηματικές σταθερές, τόσο εντός όσο και εκτός της επιστημονικής κοινότητας και έχει αποτελέσει θέμα λογοτεχνικών βιβλίων. Ο αριθμός γιορτάζεται την «ημέρα του π» και ρεκόρ υπολογισμού των ψηφίων του π συχνά αναφέρονται σε τίτλους ειδήσεων.
Βασικές αρχές[Επεξεργασία | επεξεργασία κώδικα]
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]

Ως π συχνά ορίζεται το πηλίκο της περιφέρειας ενός κύκλου προς την διάμετρό του :[1]
- .
Ο λόγος είναι σταθερός και ανεξάρτητος από το μέγεθος του κύκλου. Για παράδειγμα, αν ένας κύκλος έχει διπλάσια διάμετρο, αυτός θα έχει και διπλάσια περιφέρεια, διατηρώντας το λόγο σταθερό. Αυτός ο ορισμός του π είναι έγκυρος μόνο στην επίπεδη (Ευκλείδεια) Γεωμετρία, ενώ αν επεκταθεί σε κυρτές (Μη-Ευκλείδειες) Γεωμετρίες ο λόγος δεν παραμένει σταθερός.[1] Υπάρχουν άλλοι ορισμοί του π με βάση τον απειροστικό λογισμό ή την τριγωνομετρία που δεν βασίζονται σε κύκλο. Ένας τέτοιος ορισμός είναι: Το π είναι το διπλάσιο του μικρότερο θετικού για συν(x) ισούται με 0.[1][2]
Όνομα[Επεξεργασία | επεξεργασία κώδικα]

Το σύμβολο που χρησιμοποιείται από τους μαθηματικούς για την αναλογία της περιφέρειας ενός κύκλου προς την διάμετρό του είναι το ελληνικό γράμμα π. Αυτό το γράμμα (και ως εκ τούτου ο ίδιος ο αριθμός π) μπορεί να σημανθεί με τη Λατινική λέξη pi.[3] Το πεζό π δεν πρέπει να συγχέεται με το κεφαλαίο γράμμα , που χρησιμοποιείται για το γινόμενο όρων μιας ακολουθίας.
Η πρώτη γνωστή χρήση του ελληνικού γράμματος π για να αντιπροσωπεύσει την αναλογία της περιφέρειας ενός κύκλου προς τη διάμετρό του ήταν από τον μαθηματικό Γουίλιαμ Τζόουνς στο έργο του, το 1706, Synopsis Palmariorum Matheseos (Μια Νέα Εισαγωγή στα Μαθηματικά).[4] Το ελληνικό γράμμα πρωτοεμφανίζεται σε αυτό το έργο στην φράση « περιφέρειας (π)» σε παράγραφο σχετικά με έναν κύκλο με ακτίνα ένα. Ο Τζόουνς μπορεί να επέλεξε το π επειδή ήταν το πρώτο γράμμα στην ελληνική ορθογραφία της λέξης περιφέρεια.[5] Ωστόσο, γράφει ότι οι εξισώσεις του π είναι από την «έτοιμη πένα του πραγματικά έξυπνου κ. John Machin», οδηγώντας σε εικασίες ότι ο Μέτσιν μπορεί να χρησιμοποίησε το ελληνικό γράμμα πριν τον Τζόουνς.[6] Αυτό πράγματι είχε χρησιμοποιηθεί νωρίτερα για τις γεωμετρικές ερμηνείες.[6] Ο Γουίλιαμ Τράουτεντ χρησιμοποιεί τα ελληνικά γράμματα π και δ, για να εκφράσει αναλογίες της περιφέρειας και της διαμέτρου το 1647. Το ίδιο συμβαίνει και σε μεταγενέστερες εκδόσεις του Clavis Mathematicae.
Μετά την εισαγωγή του ελληνικού γράμματος από τον Τζόουνς το 1706, δεν υιοθετήθηκε από άλλους μαθηματικούς μέχρι ο Λέοναρντ Όιλερ να αρχίσει να το χρησιμοποιεί, ξεκινώντας με το έργο του Μηχανική το 1736. Έως τότε, οι μαθηματικοί χρησιμοποιούσαν μερικές φορές γράμματα όπως το c ή το p.[6] Ο Όιλερ συνεργαζόταν σε μεγάλο βαθμό και με άλλους μαθηματικούς στην Ευρώπη και έτσι η χρήση του π εξαπλώθηκε γρήγορα.[6] Το 1748, ο Όιλερ χρησιμοποίησε το π στο ευρέως διαβασμένο έργο του Introductio in analysin infinitorum (έγραψε: «για λόγους συντομίας θα γράφουμε τον αριθμό π· έτσι το π είναι ίσο με το μισό της περιφέρειας ενός κύκλου ακτίνας 1») και η πρακτική του εγκρίθηκε παγκοσμίως στη συνέχεια σε ολόκληρο τον Δυτικό Κόσμο.[6]
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Το π είναι ένας άρρητος αριθμός, που σημαίνει ότι αυτός δεν μπορεί να γραφεί ως πηλίκο δύο ακεραίων, όπως ή άλλα κλάσματα που χρησιμοποιούνται συνήθως για την προσέγγισή του.[7] Δεδομένου ότι το π είναι άρρητος, έχει έναν άπειρο αριθμό ψηφίων στην δεκαδική του αναπαράσταση, και αυτό δεν τελειώνει με μια απείρως επαναλαμβανόμενη σειρά ψηφίων. Υπάρχουν αρκετές αποδείξεις ότι το π είναι άρρητος αριθμός, οι οποίες γενικά απαιτούν λογισμό και επικαλούνται την εις άτοπον απαγωγή. Ο βαθμός στον οποίο μπορεί το π να είναι προσεγγιστικά ρητός αριθμός (που ονομάζεται το μέτρο της αρρητότητας) δεν είναι ακριβώς γνωστό· εκτιμήσεις καθόρισαν ότι το μέτρο της αρρητότητας είναι μεγαλύτερο από το μέτρο του ή , αλλά μικρότερο από το μέτρο των αριθμών Λιουβίλ.[8]

Ο π είναι ένας υπερβατικός αριθμός, πράγμα που σημαίνει πως δεν είναι λύση κάποιου μη-σταθερού πολυωνύμου με ρητούς συντελεστές, όπως [9][10] Η υπερβατικότητα του π έχει δύο σημαντικές επιπτώσεις: Πρώτον, ο π δεν μπορεί να εκφραστεί χρησιμοποιώντας οποιονδήποτε συνδυασμό ρητών και τετραγωνικών αριθμών ή ν-ιοστων ριζών όπως ή Δεύτερον, δεδομένου ότι δεν μπορεί να κατασκευαστεί κάποιος υπερβατικός αριθμός με κανόνα και διαβήτη, δεν είναι δυνατόν να «τετραγωνιστεί ο κύκλος». Με άλλα λόγια, είναι αδύνατο να κατασκευάσουμε, χρησιμοποιώντας μόνο κανόνα και διαβήτη, ένα τετράγωνο του οποίου το εμβαδόν να είναι ίσο προς το εμβαδόν ενός δεδομένου κύκλου.[11] Ο τετραγωνισμός του κύκλου ήταν ένα από τα σημαντικότερα γεωμετρικά προβλήματα της κλασικής αρχαιότητας.[12] Ερασιτέχνες μαθηματικοί στη σύγχρονη εποχή μερικές φορές προσπάθησαν να τετραγωνίσουν τον κύκλο, και μερικές φορές ισχυρίζονταν επιτυχία, παρά το γεγονός ότι στην πραγματικότητα είναι αδύνατο.[13]
Τα ψηφία του π δεν έχουν κάποιο προφανές μοτίβο και έχουν περάσει διάφορους στατιστικούς ελέγχους για τυχαιότητα, συμπεριλαμβανομένων δοκιμών για ομαλότητα· ένας αριθμός απείρου μήκους ονομάζεται ομαλός όταν όλες οι πιθανές ακολουθίες ψηφίων (από κάθε συγκεκριμένο μήκος) εμφανίζονται εξίσου συχνά.[14] Αυτή η υπόθεση ότι το π είναι κανονικός δεν έχει αποδειχθεί ή διαψευσθεί.[14] Μετά την έλευση των υπολογιστών, ένα μεγάλος αριθμός ψηφίων του π ήταν διαθέσιμος για να εκτελέσουμε στατιστικές αναλύσεις. Ο Γιασουμάσα Κανάντα έχει εκτελέσει λεπτομερειακώς στατιστικές αναλύσεις για τα δεκαδικά ψηφία του π· για παράδειγμα, η συχνότητα των δέκα ψηφίων 0 έως 9 υποβλήθηκαν σε στατιστικούς ελέγχους, και δεν βρέθηκε κάποια ένδειξη για ένα μοτίβο.[15] Παρά το γεγονός ότι τα ψηφία του π πέρασαν από στατιστικούς ελέγχους για την τυχαιότητα, ο π περιέχει ορισμένες ακολουθίες ψηφίων που ενδέχεται να μοιάζουν μη-τυχαίες στους μη-μαθηματικούς, όπως το σημείο Φάινμαν, που ξεκινά από το 762ο δεκαδικό ψηφίο της δεκαδικής απεικόνισης του π.[16]
Συνεχή κλάσματα[Επεξεργασία | επεξεργασία κώδικα]

Όπως όλους τους άρρητους αριθμούς, ο π δεν μπορεί να αναπαρασταθεί ως απλό κλάσμα. Αλλά κάθε άρρητος αριθμός, συμπεριλαμβανομένου του π, μπορεί να εκφραστεί από μια άπειρη σειρά ένθετων κλασμάτων, που ονομάζεται συνεχές κλάσμα:
- (
 A001203).
A001203).
Αν σταματήσουμε ένα συνεχές κλάσμα σε οποιοδήποτε σημείο, τότε δημιουργεί ένα κλάσμα, που δίνει μια προσέγγιση για το π· δύο τέτοια κλάσματα, το και το , έχουν χρησιμοποιηθεί ιστορικά για την προσέγγιση της σταθεράς. Κάθε προσέγγιση που δημιουργείται με αυτόν τον τρόπο είναι η καλύτερη προσέγγιση, με την έννοια ότι είναι πιο κοντά στο π από οποιοδήποτε άλλο κλάσμα με τον ίδιο ή μικρότερο παρονομαστή.[17] Αν και το απλό συνεχές κλάσμα για το π που δόθηκε παραπάνω δεν εμφανίζει κάποιο ένα μοτίβο,[18] οι μαθηματικοί έχουν ανακαλύψει αρκετές γενικεύσεις συνεχών κλασμάτων που έχουν μοτίβα, όπως:[19]
- .
Κατά προσέγγιση τιμή[Επεξεργασία | επεξεργασία κώδικα]
Ορισμένες προσεγγίσεις του π δίνονται παρακάτω:
- Κλάσματα: Κατά προσέγγιση κλάσματα (με αυξανόμενη ακρίβεια) , , , , και .[17]
- Δεκαδικό: τα πρώτα 100 δεκαδικά ψηφία είναι 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 ....[20]
 A000796
A000796 - Δυαδικό:
- Δεκαεξαδικό: Μια βάση προσέγγισης από 16 έως 20 ψηφία είναι [21]
- Εξηκονταδικό: Μια βάση 60 προσέγγιση είναι 3:8:29:44:1
Ιστορία του π[Επεξεργασία | επεξεργασία κώδικα]
Αρχαιότητα[Επεξεργασία | επεξεργασία κώδικα]
Η μεγάλη πυραμίδα στην Γκίζα, κατασκευασμένη το διάστημα 2589–2566 π.Χ., χτίστηκε με περίμετρο περίπου 1.760 πήχεις και ύψος περίπου 280 πήχεις· η αναλογία είναι περίπου ίση με . Με βάση αυτή την αναλογία, κάποιοι Αιγυπτιολόγοι κατέληξαν στο συμπέρασμα ότι οι οικοδόμοι της πυραμίδας είχαν γνώση του π και σκόπιμα σχεδίασαν την πυραμίδα για να ενσωματώσουν τις αναλογίες του κύκλου.[22] Άλλοι ισχυρίζονται πως η προτεινόμενη πρόταση είναι απλώς μια σύμπτωση, επειδή δεν υπάρχει κάποια απόδειξη ότι οι οικοδόμοι της πυραμίδας γνώριζαν το π, και επειδή οι διαστάσεις της πυραμίδας βασίζονται σε άλλους παράγοντες.[23]
Οι παλαιότερες γραπτές προσεγγίσεις του π βρίσκονται στην Αίγυπτο και τη Βαβυλώνα, απέχουν μόλις ένα τοις εκατό από την πραγματική αξία. Στη Βαβυλώνα, ένας δίσκος της που χρονολογείται το 1900–1600 π.Χ. έχει μια γεωμετρική δήλωση που, κατ' επέκταση, αντιμετωπίζει τον π ως 25/8 = 3.1250.[24] Στην Αίγυπτο, ο Πάπυρος Rhind, χρονολογείται γύρω στο 1650 π.Χ., αλλά έχει αντιγραφεί από ένα έγγραφο που χρονολογείται το 1850 π.Χ. έχει ένα τύπο που την αντιμετωπίζει την σταθερά π ως (16/9)2 ≈ 3.1605.[24]
Στην Ινδία γύρω στο 600 π.Χ., το Shulba Sutras (σανσκριτικά κείμενα που είναι πλούσια σε μαθηματικό περιεχόμενο) εξομοιώνει τον π με (9785/5568)2 ≈ 3.088.[25] Το 150 π.Χ., ή ίσως νωρίτερα, ινδικές πηγές θεωρούν τον π ως ≈ 3.1622.[26]
Δύο στίχοι της Εβραϊκής Βίβλου (γράφτηκε περίπου στον 8ο και 3ο αιώνα π.Χ.) περιγράφει μια τελετουργική λεκάνη στο Ναό του Σολομώντα με διάμετρο δέκα πήχεις και η περίμετρός του τριάκοντα πήχεις· Οι στίχοι υποδηλώνουν ότι ο π είναι περίπου τρία αν η λεκάνη είναι κυκλική.[27][28] Ο Rabbi Nehemiah εξήγησε τη διαφορά ως λόγω του πάχους του σκάφους. Το πρώιμο έργο της γεωμετρίας, Mishnat ha-Middot, γράφτηκε γύρω στο 150 μ.Χ. και παίρνει την τιμή του π για να είναι τρία και ένα έβδομο.[29]
Μνημονικός κανόνας[Επεξεργασία | επεξεργασία κώδικα]
Αεί (ο) Θεός (ο μέγας) γεωμετρεί
— Πλάτων
Ο Πλούταρχος αναφέρει στο έργο του Ερωτήσεις "Πῶς Πλάτων ἔλεγε τὸν θεὸν ἀεὶ γεωμετρεῖν."[30] Από αυτή τη φράση προκύπτει ο μνημονικός κανόνας «Αεί ο Θεός ο μέγας γεωμετρεί» όπου ο αριθμός των γραμμάτων δείχνει το αντίστοιχο ψηφίο του αριθμού π, με προσέγγιση 5 δεκαδικών ψηφίων (3,14159265358979...).
- Αεί = 3
- ο = 1
- Θεός = 4
- ο =1
- μέγας = 5
- γεωμετρεί = 9
Σε νεότερους χρόνους, έχει χρησιμοποιηθεί μεγαλύτερη πρόταση για περισσότερα ψηφία «Αεί ο Θεός ο Μέγας γεωμετρεί, το κύκλου μήκος ίνα ορίση διαμέτρω, παρήγαγεν αριθμόν απέραντον, καί όν, φευ, ουδέποτε όλον θνητοί θα εύρωσι».
Εποχή προσέγγισης με πολύγωνα[Επεξεργασία | επεξεργασία κώδικα]

Ο πρώτος καταγεγραμμένος αλγόριθμος για τον αυστηρό υπολογισμό της τιμής του π ήταν μια γεωμετρική προσέγγιση χρησιμοποιώντας πολύγωνα, που μελετήθηκε γύρω στο 250 π.Χ. από τον Έλληνα μαθηματικό Αρχιμήδη.[31] Αυτός ο πολυγωνικός αλγόριθμος κυριάρχησε για πάνω από 1.000 χρόνια, και ως εκ τούτου το π μερικές φορές αναφέρεται ως «σταθερά του Αρχιμήδη».[32] Ο Αρχιμήδης υπολόγισε τα ανώτερα και κατώτερα όρια του π σχεδιάζοντας ένα κανονικό εξάγωνο εσωτερικά και εξωτερικά ενός κύκλου και διαδοχικά διπλασιάζοντας το πλήθος των πλευρών, έως ότου έφτασε κανονικού 96-γωνο. Υπολογίζοντας την περίμετρο αυτών πολυγώνων, απέδειξε ότι ().[33] Το άνω όριο του Αρχιμήδη, το μπορεί να οδήγησε σε μια ευρέως διαδεδομένη δημοφιλή πεποίθηση ότι το π είναι ίσο με .[34] Περίπου το 150 μ.Χ., ο Έλληνας-Ρωμαίος επιστήμονας Πτολεμαίος, στην Αλμαγέστη, έδωσε μια τιμή για το π το 3.1416, που αυτή μπορεί να αποκτηθεί από τον Απολλώνιο του Περγαίου.[35] Οι πολυγωνικοί αλγόριθμοι χρησιμοποιήθηκα για να υπολογίσουν 39 ψηφία του π το 1630, ένα ρεκόρ που έσπασε το 1699 όταν άπειρες σειρές χρησιμοποιήθηκαν για τον υπολογισμό 71 ψηφίων.[36]

Στην Αρχαία Κίνα, οι τιμές για το π περιλαμβάνονται 3.1547 (γύρω στο 1 μ.Χ.), (100 μ.Χ, περίπου 3.1623), και (3ο αιώνα, περίπου 3.1556).[37] Περίπου το 265 μ.Χ., στο Δυτικό Βασίλειο ο μαθηματικός Liu Hui δημιούργησε ένα πολύγωνο με βάση τον επαναληπτικό αλγόριθμο και το χρησιμοποίησε με ένα πολύγωνο 3,072-διπλής όψης, για να πάρει μια τιμή του π την 3.1416.[38][39] Αργότερα ο Liu ανακάλυψε μια ταχύτερη μέθοδο υπολογισμού του π και λαμβάνεται η τιμή 3.14 με ένα πολύγωνο 96-διπλής όψης, αξιοποιώντας το γεγονός ότι οι διάφορες τιμές στην περιοχή των διαδοχικών πολυγώνων αποτελούν μια γεωμετρική σειρά με συντελεστή 4.[38] Ο Κινέζος μαθηματικός Zu Chongzhi, γύρω στο 480 μ.Χ., υπολόγισε ότι π ≈ 355/113 (ένα κλάσμα που πηγαίνει από το όνομα Milü στα Κινέζικα), χρησιμοποιώντας τον αλγόριθμο του Liu Hui εφαρμόζεται σε ένα πολύγωνο 12,288-πλευρών. Με μια σωστή τιμή για τα επτά πρώτα δεκαδικά ψηφία, αυτή η τιμή 3.141592920... παραμένει η πιο ακριβής προσέγγιση του π διαθέσιμη για τα επόμενα 800 χρόνια.[40]
Ο Ινδός αστρονόμος Αριαμπάτα χρησιμοποίησε την τιμή 3.1416 σε Āryabhaṭīya (499 μ.Χ.).[41] Ο Φιμπονάτσι το 1220 υπολόγισε 3.1418 χρησιμοποιώντας μια πολυγωνική μέθοδο, ανεξάρτητη του Αρχιμήδη.[42] Ο Ιταλός συγγραφέας Δάντης Αλιγκέρι ασχολήθηκε όπως φαίνεται με την τιμή .[42]
Ο Πέρσης αστρονόμος Jamshīd al-Kāshī παρήγαγε 16 ψηφία το 1424 χρησιμοποιώντας ένα πολύγωνο με 3×228 πλευρές,[43][44] το οποίο παραμένει το παγκόσμιο ρεκόρ για 180 περίπου χρόνια.[45] Ο Γάλλος μαθηματικός Φραγκίσκος Βιετά το 1579 κατόρθωσε να παράγει 9 ψηφία με ένα πολύγωνο με 3×217 πλευρές.[45] Ο Φλαμανδός μαθηματικός Άντριαν φαν Ρόομεν έφτασε στα 15 δεκαδικά ψηφία το 1593.[45] Το 1596, ο Ολλανδός μαθηματικός Ludolph van Ceulen έφτασε τα 20 ψηφία, ένα ρεκόρ που αργότερα αυξήθηκε στα 35 ψηφία (ως εκ τούτου, το π ονομαζόταν "αριθμός Ludolph" στη Γερμανία μέχρι τις αρχές του 20ού αιώνα).[46] Ο Ολλανδός μαθηματικός Willebrord Snellius έφτασε τα 34 ψηφία το 1621,[47] και ο Αυστριακός μαθηματικός Christoph Grienberger έφτασε τα 38 ψηφία το 1630,[48] τα οποία παραμένουν η ακριβέστερη προσέγγιση με μη αυτόματο τρόπο να επιτευχθεί χρησιμοποιώντας τον πολυγωνικό αλγόριθμο.[47]
Απειροσειρές[Επεξεργασία | επεξεργασία κώδικα]
Η ανάπτυξη τεχνικών των απειροσειρών έφεραν επανάσταση στον υπολογισμό του π, τον 16ο και τον 17ο αιώνα. Μια άπειρη σειρά είναι το άθροισμα των όρων της άπειρης ακολουθίας.[49] Μια άπειρη σειρά επιτρέπει στους μαθηματικούς να υπολογίσουν το π με μεγαλύτερη ακρίβεια από τον Αρχιμήδη και άλλους που χρησιμοποίησαν μαθηματικές τεχνικές.[49] Αν και άπειρες σειρές εκμεταλλεύτηκαν για τον π κυρίως Ευρωπαίοι μαθηματικοί, όπως ο Τζέιμς Γκρέγκορι και Γκότφριντ Βίλχελμ Λάιμπνιτς, η προσέγγιση πρώτα ανακαλύφθηκε στην Ινδία κάποια στιγμή μεταξύ 1400 και 1500 μ.Χ>.[50] Η πρώτη γραπτή περιγραφή μιας άπειρης σειράς που θα μπορούσε να χρησιμοποιηθεί για τον υπολογισμό του π τέθηκε σε σανσκριτικό στίχο από τον Ινδό αστρονόμο Nilakantha Somayaji στο Tantrasamgraha, γύρω στο 1500 μ.Χ.[51] Οι σειρές παρουσιάζονται χωρίς απόδειξη, αλλά οι αποδείξεις παρουσιάζονται σε μεταγενέστερο ινδικό έργο, Yuktibhāṣā, από το 1530 μ.Χ. περίπου. Ο Nilakantha αποδίδει τη σειρά σε έναν προηγούμενο μαθηματικό Ινδό, τον Madhava της Sangamagrama, που έζησε το 1350 – 1425 μ.Χ.[51] Πολλές σειρές που περιγράφονται, συμπεριλαμβανομένων τη σειρά για το ημίτονο, εφαπτομένη, και συνημίτονο, που τώρα αναφέρονται ως σειρά Madhava ή σειρά Gregory–Leibniz.[51] Ο Madhava χρησιμοποίησε άπειρη σειρά για να προσεγγίσει το π σε 11 δεκαδικά ψηφία περίπου το 1400, αλλά αυτή την εγγραφή νίκησε γύρω στο 1430 ο Πέρσης μαθηματικός Jamshīd al-Kāshī, χρησιμοποιώντας έναν πολυγωνικό αλγόριθμο.[52]

Η πρώτη άπειρη ακολουθία που ανακαλύφθηκε στην Ευρώπη ήταν ένα άπειρο γινόμενο (και όχι τόσο ένα άπειρο άθροισμα, το οποίο χρησιμοποιείται πιο τυπικά στους υπολογισμούς του π) και βρέθηκε από τον Γάλλο μαθηματικό Φρανσουά Βιετά το 1593:[54]
- .
 A060294
A060294
Τη δεύτερη άπειρη ακολουθία που βρέθηκε στην Ευρώπη, από τον John Wallis το 1655, ήταν επίσης ένα άπειρο προϊόν.[54] Η ανακάλυψη του λογισμού, από τον Άγγλο επιστήμονα Isaac Newton και τον Γερμανό μαθηματικό Gottfried Wilhelm Leibniz το 1660, οδήγησε στην ανάπτυξη πολλών άπειρων σειρών για την προσέγγιση του π. Ο ίδιος ο Newton χρησιμοποιεί μια σειρά arcsin για τον υπολογισμό 15 ψηφίων του π το 1665 ή 1666, αργότερα έγραψε "Ντρέπομαι να σου πω πόσα κρατούμενα είχα σε αυτούς τους υπολογισμούς, αφού καμία άλλη χρήση δεν έχουν αυτή την στιγμή."[53]
Στην Ευρώπη, ο τύπος του Madhava ανακαλύφθηκε από τον Σκοτσέζο μαθηματικό James Gregory το 1671, και από τον Λάιμπνιτς το 1674:[55][56]
- .
Αυτός ο τύπος, η σειρά του Gregory–Λάιμπνιτς, ισούται με όταν υπολογιστεί με .[56] Το 1699, ο Άγγλος μαθηματικός Abraham Sharp χρησιμοποίησε τη σειρά Gregory–Λάιμπνιτς για τον υπολογισμό του π σε 71 ψηφία, σπάζοντας το προηγούμενο ρεκόρ των 39 ψηφίων, που βρέθηκε με έναν πολυγωνικό αλγόριθμο.[57] Η σειρά Gregory–Λάιμπνιτς είναι απλή, αλλά συγκλίνει πολύ αργά (δηλαδή πλησιάζει την απάντηση σταδιακά), έτσι δεν χρησιμοποιείται στους σύγχρονους υπολογισμούς για το π.[58]
Το 1706 ο John Machin χρησιμοποίησε τη σειρά Gregory–Λάιμπνιτς για τον σχεδιασμό ενός αλγορίθμου που συγκλίνει πολύ πιο γρήγορα:[59]
- .
Ο Machin έφτασε τα 100 ψηφία του π με αυτό τον τύπο.[60] Άλλοι μαθηματικοί δημιούργησαν παραλλαγές, γνωστοί ως αλγόριθμοι τύπου Machin, που χρησιμοποιήθηκαν για να θέσουν πολλά διαδοχικά ρεκόρ για τον υπολογισμό των ψηφίων του π.[60] Ο τύπος Machin-παρέμεινε ως η πιο γνωστή μέθοδος υπολογισμού του π μέχρι και την αρχή της εποχής της πληροφορικής, και χρησιμοποιήθηκαν για να ορίσουν τις εγγραφές για 250 χρόνια, με αποκορύφωμα μια των 620-ψηφίων προσέγγιση του 1946 από τον Daniel Ferguson – την καλύτερη προσέγγιση που επιτεύχθηκε χωρίς τη βοήθεια υπολογιστής μηχανής.[61]
Αξιόλογο ρεκόρ ορίστηκε από τον υπολογισμό θαύμα του Zacharias Dase, ο οποίος το 1844 απασχολήθηκε με έναν αλγόριθμο τύπου Machin-όπως τύπο για τον υπολογισμό 200 δεκαδικών ψηφίων του π στο κεφάλι του, μετά από εντολή του Γερμανού μαθηματικού Καρλ Φρίντριχτ Γκάους.[62] Ο Βρετανός μαθηματικός William Shanks περίφημα πήρε 15 χρόνια για τον υπολογισμό π σε 707 ψηφία, αλλά έκανε ένα λάθος στο 528ο ψηφίο του, καθιστώντας όλα τα επόμενα ψηφία λανθασμένα.[62]
Αρρητότητα[Επεξεργασία | επεξεργασία κώδικα]
Κάποιες άπειρες σειρές για το π συγκλίνουν γρηγορότερα από άλλες. Με δεδομένη την επιλογή των δύο σειρών για το π, οι μαθηματικοί θα χρησιμοποιούν γενικά αυτή που συγκλίνει πιο γρήγορα επειδή η ταχύτητα σύγκλισης μειώνει την υπολογιστική ισχύ που απαιτείται για τον υπολογισμό του π σε οποιαδήποτε δεδομένη ακρίβεια.[63] Μια απλή άπειρη σειρά για π είναι η σειρά Gregory–Leibniz:[64]
- .
Καθώς οι επιμέρους όροι αυτής της άπειρης σειράς προστίθενται στο σύνολο, το σύνολο σταδιακά προσεγγίζει το π, και – με επαρκή αριθμό όρων – μπορεί να πλησιάσει περισσότερο το π όπως επιθυμείται. Συγκλίνει αρκετά αργά, αν και – μετά από 500.000 όρους, παράγει μόνο πέντε σωστά δεκαδικά ψηφία του π.[65]
Μια άπειρη σειρά για το π (δημοσιεύθηκε από τον Nilakantha τον 15ο αιώνα) που συγκλίνει πιο γρήγορα από τη σειρά Gregory–Leibniz είναι:[66]
- .
Ο ακόλουθος πίνακας συγκρίνει τα ποσοστά σύγκλισης από αυτές τις δύο σειρές:
| Άπειρη σειρά για π | Μετά τον 1ο όρο | Μετά τον 2ο όρο | Μετά τον 3ο όρο | Μετά τον 4ο όρο | Μετά τον 5ο όρο | Συγκλίνει/Προσεγγίζει το: |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666... | 3.4666... | 2.8952... | 3.3396... | π = 3.1415... | |
| 3.0000 | 3.1666... | 3.1333... | 3.1452... | 3.1396... |
Μετά από πέντε όρους, το άθροισμα της σειράς του Gregory–Leibniz είναι εντός 0.2 της σωστής τιμής του π, ενώ το ποσό της σειράς του Nilakantha είναι εντός 0.002 της σωστής τιμής του π. Η σειρά του Nilakantha συγκλίνει γρηγορότερα και είναι πιο χρήσιμη για τον υπολογισμό των ψηφίων του π. Μια σειρά που συγκλίνει ακόμη πιο γρήγορα περιλαμβάνει τη σειρά σειρά Machin και σειρά Chudnovsky, που αργότερα παρήγαγε 14 σωστά δεκαδικά ψηφία ανά όρο.[63]
Αρρητότητα και υπερβατικότητα[Επεξεργασία | επεξεργασία κώδικα]
Δεν στόχευαν όλες οι μαθηματικές πρόοδοι που αφορούν τον π στην αύξηση της ακρίβειας των προσεγγίσεων. Όταν ο Όιλερ έλυσε το πρόβλημα της Βασιλείας το 1735, βρίσκοντας την ακριβή τιμή του αθροίσματος των αμφότερων τετραγώνων, καθιέρωσε μια σχέση μεταξύ του π και των πρώτων αριθμών που αργότερα συνέβαλαν στην ανάπτυξη και τη μελέτη της συνάρτησης ζήτα του Ρίμαν:[67]
- .
Ο Ελβετός επιστήμονας Λάμπερτ το 1761 απέδειξε ότι ο π είναι άρρητος, που σημαίνει ότι δεν είναι ίσος με το πηλίκο δύο ακεραίων αριθμών.[7] Η απόδειξη του Λάμπερτ χρησιμοποιεί μία αναπαράσταση συνεχών κλασμάτων της συνάρτησης εφαπτομένης.[68] Ο Γάλλος μαθηματικός Λεζάντρ απέδειξε το 1794 ότι ο είναι επίσης άρρητος. Το 1882, ο Γερμανός μαθηματικός φον Λίντεμαν απέδειξε ότι ο π είναι υπερβατικός, επιβεβαιώνοντας την εικασία που έκαναν αμφότεροι ο Λεζάντρ και ο Όιλερ.[69]
Εποχή υπολογιστών και επαναληπτικοί αλγόριθμοι[Επεξεργασία | επεξεργασία κώδικα]

Προετοιμασία
Εύρεση
Στη συνέχεια μια εκτίμηση για το π δίνεται από
Η ανακάλυψη των υπολογιστών στα μέσα του 20ού αιώνα αναζωπύρωσαν το κυνήγι για τα ψηφία του π. Οι Αμερικανοί μαθηματικοί Τζων Ρεντς και Levi Smith έφτασαν τα 1.120 ψηφία το 1949 χρησιμοποιώντας μια αριθμομηχανή γραφείου.[70] Χρησιμοποιώντας μια άπειρη σειρά της αντίστροφης εφαπτομένης (), μια ομάδα με επικεφαλής τους George Reitwiesner και Τζον φον Νόιμαν την ίδια χρονιά ανακάλυψαν 2.037 ψηφία με τον υπολογισμό που έκανε ο υπολογιστής ENIAC σε 70 ώρες του χρόνου του υπολογιστή.[71] Την ιστορία του, επικαλείται πάντα μια σειρά , που έσπαγε επανειλημμένα τα προηγούμενα ρεκόρ (7.480 ψηφία το 1957, 10.000 ψηφία το 1958, 100.000 ψηφία το 1961) μέχρι 1 εκατομμύριο ψηφία το 1973.[72]
Δύο επιπλέον εξελίξεις γύρω στο 1980 επιτάχυναν εκ νέου τη δυνατότητα υπολογισμού του π. Πρώτον, η ανακάλυψη νέων επαναληπτικών αλγορίθμων για τον υπολογισμό του π, που ήταν πολύ πιο γρήγοροι από την άπειρη σειρά, και δεύτερον, η εφεύρεση γρήγορου πολλαπλασιασμού αλγορίθμων που θα μπορούσε να πολλαπλασιάσει μεγάλους αριθμούς πολύ γρήγορα.[73] Τέτοιοι αλγόριθμοι είναι ιδιαίτερα σημαντικοί στους σύγχρονους υπολογισμούς του π, επειδή το μεγαλύτερο μέρος του χρόνου που ξοδεύει ο υπολογιστής είναι αφιερωμένο στους πολλαπλασιασμούς.[74] Αλγόριθμοι για τον πολλαπλασιασμό περιλαμβάνουν τον αλγόριθμο Karatsuba, τον πολλαπλασιασμό Toom–Cook και μεθόδους του μετασχηματισμού Φουριέ.[75]
Οι επαναληπτικοί αλγόριθμοι δημοσιεύθηκαν ανεξάρτητα το 1975–1976 από τον Αμερικάνο φυσικό Eugene Salamin και Αυστραλιανό επιστήμονα Richard Brent.[76] Αυτοί απέφευγαν την εξάρτηση από τις άπειρες σειρές. Ένας επαναληπτικός αλγόριθμος επαναλαμβάνει έναν συγκεκριμένο υπολογισμό, όπου σε κάθε επανάληψη η είσοδος είναι η έξοδος από το προηφούμενο βήμα, και παράγει ένα αποτέλεσμα με κάθε βήμα, προσεγγίζοντας την επιθυμητή τιμή. Η προσέγγιση ανακαλύφθηκε στην πραγματικότητα πάνω από 160 χρόνια νωρίτερα από τον Καρλ Φρίντριχ Γκάους, σε αυτό που αποκαλείται τώρα αριθμητική-γεωμετρική σημασιακή μέθοδος (μέθοδος AGM) ή αλγόριθμος Γκάους–Λεζάντρ.[76] Καθώς τροποποιήθηκε από τους Salamin και Brent, επίσης αναφέρεται και ως αλγόριθμος Brent-Salamin.
Οι επαναληπτικοί αλγόριθμοι χρησιμοποιήθηκαν ευρέως μετά το 1980, επειδή είναι πιο γρήγοροι από τους αλγορίθμους που βασίζονται σε άπειρες σειρές: ενώ οι άπειρες σειρές συνήθως αυξάνουν τον αριθμό των σωστών ψηφίων αθροιστικά σε διαδοχικούς όρους, οι επαναληπτικοί αλγόριθμοι γενικά πολλαπλασιάζουν τον αριθμό των σωστών ψηφίων σε κάθε βήμα. Για παράδειγμα, ο αλγόριθμος Brent-Salamin διπλασιάζει τον αριθμό των σωστών ψηφίων σε κάθε επανάληψη. Το 1984, τα αδέρφια John και Peter Borwein από τον Καναδά παρήγαγαν έναν επαναληπτικό αλγόριθμο που τετραπλασιάζει τον αριθμό των ψηφίων σε κάθε βήμα; και το 1987, ένας που αυξάνει τον αριθμό των ψηφίων πέντε φορές σε κάθε βήμα.[77] Επαναληπτικές μέθοδοι χρησιμοποιήθηκαν από τον Ιάπωνα μαθηματικό Γιασουμάσα Κανάντα για να καθορίσουν πολλά ρεκορ για τον υπολογισμό του π μεταξύ 1995 και 2002.[78] Αυτή η ταχεία σύγκλιση έρχεται με ένα κόστος: οι επαναληπτικοί αλγόριθμοι απαιτούν σημαντικά περισσότερη μνήμη από τις άπειρες σειρές.[78]
Κίνητρα για υπολογισμό του π[Επεξεργασία | επεξεργασία κώδικα]

Για τους περισσότερους αριθμητικούς υπολογισμούς που χρειάζονται το π, ένα μικρό πλήθος ψηφίων συνήθως παρέχουν επαρκή ακρίβεια. Σύμφωνα με τους Jörg Arndt και Christoph Haenel, τριάντα εννέα ψηφία είναι επαρκή να εκτελέσουν τους περισσότερους υπολογισμούς στην κοσμολογία, γιατί αυτή η ακρίβεια είναι απαραίτητη για τον υπολογισμό του όγκου του γνωστού σύμπαντος με ακρίβεια ενός ατόμου.[79] Παρά το γεγονός αυτό, οι άνθρωποι έχουν εργαστεί έντονα για τον υπολογισμό του π σε χιλιάδες και χιλιάδες ψηφία.[80] Αυτή η προσπάθεια μπορεί να αποδοθεί εν μέρει στην ανθρώπινη μανία να σπάει ρεκόρ, και ότι ειδήσις για τέτοια επιτεύγματα σχετικά με το π συχνά γίνονται πρωτοσέλιδα σε όλο τον κόσμο.[81][82] Υπάρχουν όμως επίσης κάποια πρακτικά οφέλη, όπως σε δοκιμές υπερυπολογιστών, δοκιμές αλγορίθμων για αριθμητικές πράξεις (συμπεριλαμβανομένων αλγορίθμων για τον πολλαπλασιασμό υψηλής ακρίβειας αριθμών); και εντός των καθαρών μαθηματικών, παρέχουν στοιχεία για την αξιολόγηση της τυχαιότητας των ψηφίων του π.[83]
Γρήγορα συγκλίνουσες σειρές[Επεξεργασία | επεξεργασία κώδικα]

Οι σύγχρονοι αλγόριθμοι για το π δεν χρησιμοποιούν αποκλειστικά τους επαναληπτικούς αλγόριθμους. Νέες άπειρες σειρές ανακαλύφθηκαν στις δεκαετίες του 1980 και του 1990 που είναι τόσο γρήγορες όσο και οι επαναληπτικοί αλγόριθμοι, όμως είναι απλούστερες και απαιτούν λιγότερη μνήμη.[78] Οι γρήγοροι επαναληπτικοί αλγόριθμοι εμφανίστηκαν το 1914, όταν ο Ινδός μαθηματικός Σρινιβάσα Ραμανούτζαν δημοσίευσε δεκάδες καινούργιους τύπους για το π, που ήταν αξιοπρόσεκτοι για την κομψότητά τους, το μαθηματικό βάθος, και την ταχεία τους σύγκλιση.[84] Ένας από τους τύπους, είναι ο εξής:
- .
Αυτή η σειρά συγκλίνει γρηγορότερα από τη σειρά , συμπεριλαμβανομένου του τύπου Machin.[85] Ο Bill Gosper ήταν ο πρώτος που τον χρησιμοποίησε για τον υπολογισμό του π, θέτοντας ένα ρεκόρ των 17 εκατομμυρίων ψηφίων το 1985.[86] Ο τύπος του Ramanujan έστρωσε τον δρόμο για τους σύγχρονους αλγορίθμους που αναπτύχθηκαν από τους αδερφούς Borwein και τους αδερφούς Chudnovsky.[87] Ο τύπος των Chudnovsky που αναπτύχθηκε το 1987 είναι
- .
Παράγει περίπου 14 ψηφία του π ανά όρο,[88] και έχει χρησιμοποιηθεί για αρκετά ρεκόρ για τον υπολογισμό ψηφίων του π, συμπεριλαμβανομένου του πρώτου που ξεπέρασε τα 109 ψηφία το 1989 από τα αδέλφια Chudnovsky, 2.7 τρισεκατομμύρια (2.7×1012) ψηφία από τον Fabrice Bellard το 2009, και 10 τρισεκατομμύρια (1013) ψηφία το 2011 από τους Alexander Yee και Shigeru Kondo.[89][90]
Το 2006, ο Καναδός μαθηματικός Simon Plouffe χρησιμοποίησε τον αλγόριθμο ακεραίων σχέσεων PSLQ[91] για να παράγει αρκετές νέες μορφές τύπων για το π, που έχουν την εξής μορφή:
- ,
όπου είναι η , είναι ένας περιττός αριθμός, και είναι ορισμένοι ρηττοί αριθμοί που υπολόγισε ο Plouffe .[92]
Αλγόριθμοι βρύσης[Επεξεργασία | επεξεργασία κώδικα]
Δύο αλγόριθμοι που επινοήθηκαν το 1995 άνοιξαν νέους δρόμους στην έρευνα του π. Καλούνται αλγόριθμοι βρύσης (tap/spigot) επειδή, όπως το νερό που στάζει από μια βρύση, παράγουν μονά ψηφία του π που δεν ξαναχρησιμοποιούνται όταν αυτά υπολογιστούν.[93][94] Αυτό είναι σε αντίθεση με τις άπειρες σειρές ή τους επαναληπτικούς αλγόριθμους, που θα διατηρήσουν και θα χρησιμοποιήσουν όλα τα ενδιάμεσα ψηφία μέχρι να παραχθεί το τελικό αποτέλεσμα.[93]
Οι Αμερικανοί μαθηματικοί Stan Wagon και Stanley Rabinowitz παρήγαγαν ένα αλγόριθμο βρύσης το 1995.[94][95][96] Η ταχύτητά του συγκρίνεται με αλγόριθμους , αλλά δεν είναι τόσο γρήγορος όσο ο επαναληπτικός αλγόριθμος.[95]
Άλλος αλγόριθμος βρύσης, ο αλγόριθμος BBP, ανακαλύφθηκε το 1995 από τον Simon Plouffe:[97][98]
- .
Αυτός ο τύπος, σε αντίθεση με άλλους προγενέστερους από αυτόν, μπορεί να παράγει κάθε δεκαεξαδικό ψηφίο του π χωρίς τον υπολογισμό όλων των προηγούμενων ψηφίων του.[97] Κάθε οκταδικό ή δυαδικό ψηφίο μπορεί να υπολογιστεί από ένα δεκαεξαδικό ψηφίο. Παραλλαγές του αλγορίθμου που έχουν ανακαλυφθεί, αλλά δεν έχει ακόμα ανακαλυφθεί ο αλγόριθμος εξόρυξης ψηφίων που θα παράγει γρήγορα τα δεκαδικά ψηφία .[99] Μια σημαντική εφαρμογή των αλγορίθμων εξόρυξης ψηφίων είναι να επικυρώσει τις νέες απαιτήσεις των υπολογιστικών ρεκόρ π: μετά από μια νέα εγγραφή που ζητήθηκε, το δεκαδικό αποτέλεσμα μετατρέπεται σε δεκαεξαδικό, και στη συνέχεια ένας αλγόριθμος εξόρυξης ψηφίων χρησιμοποιείται για τον υπολογισμό αρκετών τυχαίων δεκαδικών ψηφίων κοντά στο τέλος; Αν ταιριάζουν, αυτό παρέχει ένα μέτρο της εμπιστοσύνης ότι ολόκληρος ο υπολογισμός είναι σωστός.[90]
Ανάμεσα στο 1998 και 2000, το κατανεμημένο υπολογιστικό έργο PiHex χρησιμοποιεί τον τύπο Bellard (μια τροποποίηση του αλγορίθμου BBP) για τον υπολογισμό του πρώτου τετράκις εκατομμυριοστού (1015ο) δυαδικού ψηφίου του π, το οποίο αποδείχτηκε ότι ήταν 0.[100] Το Σεπτέμβριο του 2010, ένας υπάλληλος του Yahoo! χρησιμοποίησε τις το σύστημα Hadoop της εταιρείας σε χίλιους υπολογιστές για διάστημα πάνω από 23 μέρες για τον υπολογισμό 256 δυαδικών ψηφίων του π με το δεύτερο τετράκις εκατομμυριοστό (2×1015ο) δυαδικό ψηφίο, το οποίο επίσης συμβαίνει να είναι μηδέν.[101]
Μέθοδοι Μόντε Κάρλο[Επεξεργασία | επεξεργασία κώδικα]
Οι μέθοδοι Μόντε Κάρλο, οι οποίες χρησιμοποιούν πολλές τυχαίες δοκιμές για να υπολογίσουν ένα αποτέλεσμα, μπορούν να χρησιμοποιηθούν για να δώσουν προσεγγίσεις για το π.[102] Η βελόνα του Buffon είναι μία τέτοια δοκιμή: Αν μία βελόνα με μήκος ℓ ριχτεί n φορές σε μία επιφάνεια στην οποία είναι ζωγραφισμένες παράλληλες ευθείες σε απόσταση t μεταξύ τους, και αν x (με x > 0) από αυτές τις φορές η βελόνα κατασταλάξει έτσι ώστε να τέμνεται με μία ευθεία, τότε μπορούμε να προσεγγίσουμε το π με βάση αυτό το πλήθος:[103]
- .
Μία άλλη, πιο απλή, μέθοδος Μόντε Κάρλο για τον υπολογισμό του π είναι να χαράξουμε έναν κύκλο εγγεγραμμένο σε ένα τετράγωνο, και τυχαία να διαλέξουμε σημεία μέσα στο τετράγωνο. Η αναλογία των σημείων που είναι μέσα στο τετράγωνο προς το συνολικό πλήθος των σημείων έχει αναμενόμενη τιμή το π/4.[104]

Ένας άλλος τρόπος για να υπολογίσουμε το π με την χρήση πιθανότητας είναι να ξεκινήσουμε με έναν τυχαίο περίπατο, που καθορίζεται από μία ακολουθία δίκαιων ρίψεων νομίσματος, δηλαδή τις τυχαίες μεταβλητές Xk τέτοιες ώστε Xk ∈ {−1,1} με ίση πιθανότητα. Ο τυχαίος περίπατος ορίζεται ως
- ,
έτσι ώστε, για κάθε n, το Wn έχει μία διωνυμική κατανομή. Από τις ιδιότητες της διωνυμικής κατανομής προκύπτει ότι[105]
Αυτή η μέθοδος Μόντε Κάρλο είναι ανεξάρτητη της σχέσης του π με τους κύκλους, και είναι αποτέλεσμα του θεωρήματος κεντρικού ορίου.
Αυτές οι μέθοδοι Μόντε Κάρλο για τον υπολογισμό του π είναι πολύ αργές σε σχέση με άλλες μεθόδους, και δεν δίνουν κάποια πληροφορία για το πόσα ψηφία έχουν υπολογιστεί ανά πάσα στιγμή. Επομένως δεν χρησιμοποιούνται για τον υπολογισμό του π όταν χρειάζονται πολλά ψηφία γρήγορα.[106]
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Υπολογισμός του π με την μέθοδο του Αρχιμήδη
- Μέθοδος Μόντε Κάρλο για τον υπολογισμό του π
- Η βελόνα του Buffon
- Προσέγγιση π με βάση τα σημεία που φαίνονται σε ένα πλέγμα
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 1,2 Arndt Haenel, 2006, p.8
- ↑ Rudin, Walter (1976). Principles of Mathematical Analysis. McGraw-Hill. ISBN 0-07-054235-X., σελ. 183.
- ↑ Holton, David; Mackridge, Peter (2004). Greek: an Essential Grammar of the Modern Language. Routledge. ISBN 0-415-23210-4., p. xi.
- ↑ Arndt & Haenel 2006, σελ. 165. A facsimile of Jones' text is in Berggren, Borwein & Borwein 1997, σελίδες 108–109
- ↑ Δείτε Schepler 1950, σελ. 220: Ο William Oughtred χρησιμοποίησε το γράμμα π για να αναπαραστήσει την περιφέρεια ενός κύκλου.
- ↑ 6,0 6,1 6,2 6,3 6,4 Arndt & Haenel 2006, σελ. 166
- ↑ 7,0 7,1 Arndt & Haenel 2006, σελ. 5
- ↑ Salikhov, V. (2008). «On the Irrationality Measure of pi». Russian Mathematical Survey 53 (3): 570. doi:. Bibcode: 2008RuMaS..63..570S.
- ↑ Mayer, Steve. «The Transcendence of π». Αρχειοθετήθηκε από το πρωτότυπο στις 29 Σεπτεμβρίου 2000. Ανακτήθηκε στις 4 Νοεμβρίου 2007.
- ↑ Το πολυώνυμο αυτό είναι οι πρώτοι όροι της σειράς Τέιλορ για την συνάρτηση του ημιτόνου.
- ↑ Posamentier & Lehmann 2004, σελ. 25
- ↑ Eymard & Lafon 1999, σελ. 129
- ↑ Beckmann 1989, σελ. 37
Schlager, Neil· Lauer, Josh (2001). Science and Its Times: Understanding the Social Significance of Scientific Discovery. Gale Group. ISBN 0-7876-3933-8., p 185. - ↑ 14,0 14,1 Arndt & Haenel 2006, σελίδες 22–23
Preuss, Paul (23 July 2001). «Are The Digits of Pi Random? Lab Researcher May Hold The Key». Lawrence Berkeley National Laboratory. Αρχειοθετήθηκε από το πρωτότυπο στις 2007-10-20. https://web.archive.org/web/20071020010208/http://lbl.gov/Science-Articles/Archive/pi-random.html. Ανακτήθηκε στις 10 November 2007. - ↑ Arndt & Haenel 2006, σελίδες 22, 28–30
- ↑ Arndt & Haenel 2006, σελ. 3
- ↑ 17,0 17,1 Eymard & Lafon 1999, σελ. 78
- ↑ Sloane, N. J. A. (επιμ.). «Sequence A001203 (Continued fraction for Pi)». The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 12 April 2012.
- ↑ Lange, L. J. (May 1999). «An Elegant Continued Fraction for π». The American Mathematical Monthly 106 (5): 456–458. doi:. https://archive.org/details/sim_american-mathematical-monthly_1999-05_106_5/page/456.
- ↑ Arndt & Haenel 2006, σελ. 240
- ↑ Arndt & Haenel 2006, σελ. 242
- ↑ "Μπορούμε να συμπεράνουμε ότι παρόλου που οι αρχαίοι Αιγύπτιοι δεν μπορούσαν να ορίσουν με ακρίβεια την τιμή του π, στην πράξη την χρησιμοποιούσαν". Verner, M. (2003). The Pyramids: Their Archaeology and History. https://archive.org/details/pyramidstheirarc0000vern., σελ. 70.
Petrie (1940). Wisdom of the Egyptians. https://archive.org/details/wisdomofegyptian0000petr., σελ. 30.
Δείτε επίσης Legon, J. A. R. (1991). «On Pyramid Dimensions and Proportions». Discussions in Egyptology 20: 25–34. Αρχειοθετήθηκε από το πρωτότυπο στις 2011-07-18. https://web.archive.org/web/20110718144356/http://www.legon.demon.co.uk/pyrprop/propde.htm. Ανακτήθηκε στις 2013-05-31..
Δείτε επίσης Petrie, W. M. F. (1925). «Surveys of the Great Pyramids». Nature Journal 116 (2930): 942–942. doi:. Bibcode: 1925Natur.116..942P. - ↑ Αιγυπτιολόγος: Rossi, Corinna (2004). Architecture and Mathematics in Ancient Egypt. Cambridge University Press. σελίδες 60–70, 200. ISBN 9780521829540.
Σκεπτικιστές: Michael Shermer (2002). The Skeptic Encyclopedia of Pseudoscience. ABC-CLIO. σελίδες 407–408. ISBN 9781576076538..
Δείτε επίσης Fagan, Garrett G. (2006). Archaeological Fantasies: How Pseudoarchaeology Misrepresents The Past and Misleads the Public. Routledge. ISBN 9780415305938..
Για μία λίστα από εξηγήσεις για το σχήμα που δεν εμπλέκει το π, δείτε Roger Herz-Fischler (2000). The Shape of the Great Pyramid. Wilfrid Laurier University Press. σελίδες 67–77, 165–166. ISBN 9780889203242. - ↑ 24,0 24,1 Arndt & Haenel 2006, σελ. 167
- ↑ Arndt & Haenel 2006, σελίδες 168–169
- ↑ Arndt & Haenel 2006, σελ. 169
- ↑ The verses are 1 Kings 7:23 and 2 Chronicles 4:2; see Arndt & Haenel 2006, σελ. 169, Schepler 1950, σελ. 165, and Beckmann 1989, σελίδες 14–16.
- ↑ Suggestions that the pool had a hexagonal shape or an outward curving rim have been offered to explain the disparity. See Borwein, Jonathan M.· Bailey, David H. (2008). Mathematics by Experiment: Plausible Reasoning in the 21st century (revised 2nd έκδοση). A. K. Peters. ISBN 978-1-56881-442-1., pp. 103, 136, 137.
- ↑ James A. Arieti, Patrick A. Wilson (2003). The Scientific & the Divine. Rowman & Littlefield. σελίδες 9–10. ISBN 9780742513976.
- ↑ Plutarch, Quaestiones Convivales, βοοκ 8, Πῶς Πλάτων ἔλεγε τὸν θεὸν ἀεὶ γεωμετρεῖν
- ↑ Arndt & Haenel 2006, σελ. 170
- ↑ Arndt & Haenel 2006, σελίδες 175, 205
- ↑ «The Computation of Pi by Archimedes: The Computation of Pi by Archimedes – File Exchange – MATLAB Central». Mathworks.com. Ανακτήθηκε στις 12 Μαρτίου 2013.
- ↑ Arndt & Haenel 2006, σελ. 171
- ↑ Arndt & Haenel 2006, σελ. 176
Boyer & Merzbach 1991, σελ. 168 - ↑ Arndt & Haenel 2006, σελίδες 15–16, 175, 184–186, 205. Ο Grienberger πέτυχε 39 ψηφία το 1630; Ο Sharp 71 ψηφία το 1699.
- ↑ Arndt & Haenel 2006, σελίδες 176–177
- ↑ 38,0 38,1 Boyer & Merzbach 1991, σελ. 202
- ↑ Arndt & Haenel 2006, σελ. 177
- ↑ Arndt & Haenel 2006, σελ. 178
- ↑ Arndt & Haenel 2006, σελίδες 179
- ↑ 42,0 42,1 Arndt & Haenel 2006, σελίδες 180
- ↑ Azarian, Mohammad K. (2010). [[1][νεκρός σύνδεσμος] «al-Risāla al-muhītīyya: A Summary»] (PDF). Missouri Journal of Mathematical Sciences 22 (2): 64–85. [2][νεκρός σύνδεσμος].[νεκρός σύνδεσμος]
- ↑ O’Connor, John J.· Robertson, Edmund F. (1999). «Ghiyath al-Din Jamshid Mas'ud al-Kashi». MacTutor History of Mathematics archive. Ανακτήθηκε στις 11 Αυγούστου 2012.
- ↑ 45,0 45,1 45,2 Arndt & Haenel 2006, σελ. 182
- ↑ Arndt & Haenel 2006, σελίδες 182–183
- ↑ 47,0 47,1 Arndt & Haenel 2006, σελ. 183
- ↑ Grienbergerus, Christophorus (1630). Elementa Trigonometrica (PDF) (στα Λατινικά). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 1 Φεβρουαρίου 2014. Ανακτήθηκε στις 31 Μαΐου 2013. Ο υπολογισμός του ήταν 3.14159 26535 89793 23846 26433 83279 50288 4196 < π < 3.14159 26535 89793 23846 26433 83279 50288 4199.
- ↑ 49,0 49,1 Arndt & Haenel 2006, σελίδες 185–191
- ↑ Roy 1990, σελίδες 101–102
Arndt & Haenel 2006, σελίδες 185–186 - ↑ 51,0 51,1 51,2 Roy 1990, σελίδες 101–102
- ↑ Joseph 1991, σελ. 264
- ↑ 53,0 53,1 Arndt & Haenel 2006, σελ. 188. Όπως αναφέρει ο Arndt.
- ↑ 54,0 54,1 Arndt & Haenel 2006, σελ. 187
- ↑ Arndt & Haenel 2006, σελίδες 188–189
- ↑ 56,0 56,1 Eymard & Lafon 1999, σελίδες 53–54
- ↑ Arndt & Haenel 2006, σελ. 189
- ↑ Arndt & Haenel 2006, σελ. 156
- ↑ Arndt & Haenel 2006, σελίδες 192–193
- ↑ 60,0 60,1 Arndt & Haenel 2006, σελίδες 72–74
- ↑ Arndt & Haenel 2006, σελίδες 192–196, 205
- ↑ 62,0 62,1 Arndt & Haenel 2006, σελίδες 194–196
- ↑ 63,0 63,1 Borwein, J. M.; Borwein, P. B. (1988). «Ramanujan and Pi». Scientific American 256 (2): 112–117. doi:. Bibcode: 1988SciAm.258b.112B.
Arndt & Haenel 2006, σελίδες 15–17, 70–72, 104, 156, 192–197, 201–202 - ↑ Arndt & Haenel 2006, σελίδες 69–72
- ↑ Borwein, J. M.; Borwein, P. B.; Dilcher, K. (1989). «Pi, Euler Numbers, and Asymptotic Expansions». American Mathematical Monthly 96 (8): 681–687. doi:. https://archive.org/details/sim_american-mathematical-monthly_1989-10_96_8/page/681.
- ↑ Arndt & Haenel 2006, σελ. 223, (τύπος 16.10). Παρατηρήστε ότι (n − 1)n(n + 1) = n3 − n.
Wells, David (1997). The Penguin Dictionary of Curious and Interesting Numbers (revised έκδοση). Penguin. σελ. 35. ISBN 978-0-140-26149-3. - ↑ Posamentier & Lehmann 2004, σελίδες 284
- ↑ Lambert, Johann, "Mémoire sur quelques propriétés remarquables des quantités transcendantes circulaires et logarithmiques", ανατύπωση στο Berggren, Borwein & Borwein 1997, σελίδες 129–140
- ↑ Arndt & Haenel 2006, σελ. 196
- ↑ Arndt & Haenel 2006, σελίδες 205
- ↑ Arndt & Haenel 2006, σελ. 197. Δείτε επίσης Reitwiesner 1950.
- ↑ Arndt & Haenel 2006, σελ. 197
- ↑ Arndt & Haenel 2006, σελίδες 15–17
- ↑ Arndt & Haenel 2006, σελίδες 131
- ↑ Arndt & Haenel 2006, σελίδες 132, 140
- ↑ 76,0 76,1 Arndt & Haenel 2006, σελ. 87
- ↑ Arndt & Haenel 2006, σελίδες 111 (5 times); pp. 113–114 (4 times).
Δείτε Borwein & Borwein 1987 για τις λεπτομέρειες των αλγορίθμων. - ↑ 78,0 78,1 78,2 Bailey, David H. (16 Μαΐου 2003). «Some Background on Kanada's Recent Pi Calculation» (PDF). Ανακτήθηκε στις 12 Απριλίου 2012.
- ↑ Arndt & Haenel 2006, σελ. 17. "39 ψηφία του π είναι αρκετά για να υπολογίσουμε τον όγκο του σύμπαντος στο πλησιέστερο άτομο."
Συνυπολογίζοντας τα επιπλέον ψηφία που χρειάζονται για να εξαληφθούν τα λάθη λόγω στρογγυλοποίησης, ο Arndt συμπεραίνει ότι μερικά εκατοντάδες ψηφία θα ήταν αρκετά για κάθε επιστημονική εφαρμογή. - ↑ Arndt & Haenel 2006, σελίδες 17–19
- ↑ Schudel, Matt (25 March 2009). «John W. Wrench, Jr.: Mathematician Had a Taste for Pi». The Washington Post: σελ. B5.
- ↑ «The Big Question: How close have we come to knowing the precise value of pi?». The Independent. 8 January 2010. http://www.independent.co.uk/news/science/the-big-question-how-close-have-we-come-to-knowing-the-precise-value-of-pi-1861197.html. Ανακτήθηκε στις 14 April 2012.
- ↑ Arndt & Haenel 2006, σελ. 18
- ↑ Arndt & Haenel 2006, σελίδες 103–104
- ↑ Arndt & Haenel 2006, σελ. 104
- ↑ Arndt & Haenel 2006, σελίδες 104, 206
- ↑ Arndt & Haenel 2006, σελίδες 110–111
- ↑ Eymard & Lafon 1999, σελ. 254
- ↑ Arndt & Haenel 2006, σελίδες 110–111, 206
Bellard, Fabrice, "Computation of 2700 billion decimal digits of Pi using a Desktop Computer", 11 Feb 2010. - ↑ 90,0 90,1 "Round 2... 10 Trillion Digits of Pi", NumberWorld.org, 17 Oct 2011. Retrieved 30 May 2012.
- ↑ Τα αρχικά PSLQ αντιστοιχούν στα Partial Sum of Least Squares, που σημαίνει μερικό άθροισμα ελαχίστων τετραγώνων.
- ↑ Plouffe, Simon (Απριλίου 2006). «Identities inspired by Ramanujan's Notebooks (part 2)» (PDF). Ανακτήθηκε στις 10 Απριλίου 2009.
- ↑ 93,0 93,1 Arndt & Haenel 2006, σελίδες 77–84
- ↑ 94,0 94,1 Gibbons, Jeremy, "Unbounded Spigot Algorithms for the Digits of Pi", 2005. Ο Gibbons δημοσίευεσε μία βελτιωμένη έκδοση του αλγόριθμου του Wagon.
- ↑ 95,0 95,1 Arndt & Haenel 2006, σελ. 77
- ↑ Rabinowitz, Stanley; Wagon, Stan (March 1995). «A spigot algorithm for the digits of Pi». American Mathematical Monthly 102 (3): 195–203. doi:. https://archive.org/details/sim_american-mathematical-monthly_1995-03_102_3/page/195. Ο κώδικας για το πρόγραμμα που υλοποιεί τον αλγόριθμο βρύσης του Wagon χρησιμοποιεί μόνο 120 χαρακτήρες.
- ↑ 97,0 97,1 Arndt & Haenel 2006, σελίδες 117, 126–128
- ↑ Bailey, David H.; Borwein, Peter B.; and Plouffe, Simon (April 1997). «On the Rapid Computation of Various Polylogarithmic Constants» (PDF). Mathematics of Computation 66 (218): 903–913. doi:. http://crd-legacy.lbl.gov/~dhbailey/dhbpapers/digits.pdf.
- ↑ Arndt & Haenel 2006, σελ. 128. Ο Plouffe δημοσίευσε έναν αλγόριθμο που υπολογίζει τα δεκαδικά ψηγία του π, αλλά είναι πιο αργός από τον ακριβή υπολογισμό όλων των προηγούμενων ψηφίων.
- ↑ Arndt & Haenel 2006, σελ. 20
Bellards formula in: Bellard, Fabrice. «A new formula to compute the nth binary digit of pi». Αρχειοθετήθηκε από το πρωτότυπο στις 12 Σεπτεμβρίου 2007. Ανακτήθηκε στις 27 Οκτωβρίου 2007. - ↑ Palmer, Jason (16 September 2010). «Pi record smashed as team finds two-quadrillionth digit». BBC News. http://www.bbc.co.uk/news/technology-11313194. Ανακτήθηκε στις 26 March 2011.
- ↑ Arndt & Haenel 2006, σελ. 39
- ↑ Ramaley, J.F. (October 1969). «Buffon's Noodle Problem». The American Mathematical Monthly 76 (8): 916–918. doi:. https://archive.org/details/sim_american-mathematical-monthly_1969-10_76_8/page/916.
- ↑ Arndt & Haenel 2006, σελίδες 39–40
Posamentier & Lehmann 2004, σελ. 105 - ↑ Grünbaum, B. (1960). «Projection Constants». Transactions of the American Mathematical Society 95 (3): 451–465. doi:.
- ↑ Arndt & Haenel 2006, σελίδες 43
Posamentier & Lehmann 2004, σελίδες 105–108
| |||||||||||||||||||||||||||||
|
















![{\displaystyle \scriptstyle {\sqrt[{3}]{31}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0cd59a4a8f498c58e6c90241ca42e657e3cbe870)
![{\displaystyle \scriptstyle {\sqrt[{2}]{10}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bbf57ab4a4bf9e3cec3236ad4718beae814bb92)














































![{\displaystyle \pi =\lim _{n\to \infty }{\frac {2n}{E[|W_{n}|]^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a691be63815c6b7d9fe15070ae98039d9c1d0384)











