Λογάριθμος

Λογάριθμος (με βαση α) ενός θετικού αριθμού θ είναι ο εκθέτης στον οποίο πρέπει να υψωθεί ένας δεδομένος αριθμός α , που λέγεται βάση, ώστε να πάρουμε αποτέλεσμα τον Θ. Για τη βάση α ισχύει ότι 0<α<1 ή α>1. Για παράδειγμα ο λογάριθμος του 1000 με βάση το 10 είναι 3, επειδή το 1000 ισούται με 10 υψωμένο εις την 3:1000 = 103 = 10 × 10 × 10. Πιο γενικά, αν x = by τότε το y είναι ο λογάριθμος του x με βάση το b, και γράφεται logb(x), έτσι log10(1000) = 3.
Οι λογάριθμοι εισήχθησαν από τον Τζον Νάπιερ στις αρχές του 17ου αιώνα ως μέσο για την απλοποίηση των υπολογισμών. Υιοθετήθηκαν με ραγδαίους ρυθμούς από επιστήμονες, μηχανικούς και άλλους ώστε να κάνουν πράξεις με λογαριθμικούς κανόνες και πίνακες λογαρίθμων. Αυτές οι μέθοδοι υπολογισμού βασίζονται στο, σημαντικό από μόνο του, γεγονός ότι ο λογάριθμος ενός γινομένου ισούται με το άθροισμα των λογαρίθμων των παραγόντων του:
Η σημερινή έννοια των λογαρίθμων προέρχεται από τον Λέοναρντ Όιλερ, ο οποίος τους συνέδεσε με την εκθετική συνάρτηση τον 18ο αιώνα.
Ο λογάριθμος με βάση το b = 10 αποκαλείται κοινός λογάριθμος και έχει πολλές εφαρμογές στην επιστήμη και τη μηχανική. Ο φυσικός λογάριθμος έχει ως βάση την σταθερά e (≈ 2.718), και η χρήση του είναι διαδεδομένη στα καθαρά μαθηματικά, και ειδικότερα στον λογισμό. Ο δυαδικός λογάρισθμος έχει ως βάση τον αριθμό b = 2 και αποτελεί σημαντικό στοιχείο της επιστήμης υπολογιστών.
Οι λογαριθμικές κλίμακες περιορίζουν το πεδίο τιμών ποσοτήτων με μεγάλο εύρος. Για παράδειγμα το ντεσιμπέλ είναι λογαριθμική μονάδα μέτρησης της διαφοράς στάθμης φυσικών μεγεθών. Στη χημεία, το pH είναι λογαριθμική μονάδα της οξύτητας ενός υδατικού διαλύματος. Οι λογάριθμοι είναι κοινός τόπος στους επιστημονικούς τύπους, στις μετρήσεις της πολυπλοκότητας των αλγορίθμων και στα γεωμετρικά αντικείμενα που ονομάζονται φράκταλ. Περιγράφουν μουσικά διαστήματα, εμφανίζονται σε τύπους που μετρούν το πλήθος των πρώτων αριθμών, χρησιμοποιούνται σε μοντέλα της ψυχοφυσικής και επικουρούν την δικανική λογιστική
Κατά τον ίδιο τρόπο με τον οποίο ο λογάριθμος αντιστρέφει την ύψωση σε δύναμη, ο μιγαδικός λογάριθμος είναι η αντίστροφη συνάρτηση της εκθετικής συνάρτησης εφαρμοζόμενης στους μιγαδικούς αριθμούς. Ο διακριτός λογάριθμος είναι μια άλλη παραλλαγή η οποία έχει εφαρμογές στην κρυπτογράφηση δημοσίου κλειδιού.
Προέλευση και ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Η ιδέα του λογαρίθμου είναι να αντιστραφεί η πράξη της ύψωσης σε δύναμη. Για παράδειγμα, η τρίτη δύναμη (κύβος) του 2 είναι το 8, επειδή το 8 είναι το γινόμενο τριών παραγόντων ίσων με 2:
Κατά συνέπεια ο λογάριθμος του 8 με βάση το 2 είναι το 3.
Ύψωση σε δύναμη[Επεξεργασία | επεξεργασία κώδικα]
Η τρίτη δύναμη ενός αριθμού b είναι το γινόμενο 3 παραγόντων, κάθε ένας από τους οποίους είναι το b. Γενικότερα, η ύψωση του b στη n-στή δύναμη, όπου n είναι ένας φυσικός αριθμός, γίνεται πολλαπλασιάζοντας n παράγοντες b. Η n-στή δύναμη του b γράφεται bn, έτσι
Η n-στή δύναμη του b, bn, ορίζεται όταν ο b είναι θετικός αριθμός και ο n είναι πραγματικός αριθμός. Για παράδειγμα b−1 είναι ο Αντίστροφος του b, δηλαδή 1/b.[σημ. 1]
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Ο λογάριθμος ενός αριθμού y ως προς βάση b είναι η δύναμη στην οποία πρέπει να υψωθεί ο b ώστε να παραχθεί ο y. Με άλλα λόγια ο λογάριθμος του y με βάση το b είναι η λύση x της εξίσωσης[2]
Ο λογάριθμος συμβολίζεται logb(y) (διαβάζεται ως «λογάριθμος του y με βάση το b»). Για να ορίζεται ο λογάριθμος, θα πρέπει η βάση b να είναι θετικός πραγματικός αριθμός μη ίσος με 1 και ο y να είναι θετικός αριθμός.[σημ. 2]
Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]
Για παράδειγμα log2(16) = 4, καθώς 24 = 2 ×2 × 2 × 2 = 16. Ο λογάριθμος μπορεί να είναι και αρνητικός:
καθώς
Ένα τρίτο παράδειγμα: log10(150) ισούται περίπου με 2,176, το οποίο βρίσκεται μεταξύ 2 και 3, καθώς το 150 βρίσκεται μεταξύ 102 = 100 και 103 = 1000. Τέλος, για οποιαδήποτε βάση b, logb(b) = 1 and logb(1) = 0 καθώς b1 = b και b0 = 1, αντίστοιχα.
Λογαριθμικές ταυτότητες[Επεξεργασία | επεξεργασία κώδικα]
Αρκετοί σημαντικοί τύποι, που αποκαλούνται και λογαριθμικές ταυτότητες, συσχετίζουν τους λογάριθμους μεταξύ τους.[3]
Γινόμενο, πηλίκο, δύναμη και ρίζα[Επεξεργασία | επεξεργασία κώδικα]
Ο λογάριθμος ενός γινομένου ισούται με το άθροισμα των λογαρίθμων των παραγόντων του. Ο λογάριθμος του λόγου δύο αριθμών ισούται με την διαφορά των λογαρίθμων τους. Συνεπώς ο λογάριθμος της n-στής δύναμης ενός αριθμού ισούται με n φορές τον λογάριθμο του αριθμού αυτού, ενώ ο λογάριθμος της n-στής ρίζας του αριθμού ισούται με τον λογάριθμό του διαιρεμένο δια n. Στον παρακάτω πίνακα φαίνονται αυτές οι ταυτότητες μαζί με παραδείγματα:
| Τύπος | Παράδειγμα | |
|---|---|---|
| γινόμενο | ||
| πηλίκο | ||
| δύναμη | ||
| ρίζα |
Αλλαγή βάσης[Επεξεργασία | επεξεργασία κώδικα]
Ο λογάριθμος logb(x) μπορεί να υπολογιστεί από τους λογαρίθμους του x και του b ως προς μία αυθαίρετη βάση k χρησιμοποιώντας τον ακόλουθο τύπο:
Τα τυπικά επιστημονικά κομπιουτεράκια υπολογίζουν λογάριθμους με βάση 10 και e.[4] Οι λογάριθμοι ως προς οποιαδήποτε βάση μπορούν από κει και πέρα να υπολογιστούν χρησιμοποιώντας οποιονδήποτε από τους δύο λογαρίθμους στον προηγούμενο τύπο:
Δεδομένου ενός αριθμού x και του λογαρίθμου του logb(x) ως προς άγνωστη βάση b, η βάση δίνεται από τον τύπο:
Ειδικές βάσεις[Επεξεργασία | επεξεργασία κώδικα]
Ανάμεσα σε όλες τις επιλογές για την βάση b, τρεις είναι ιδιαίτερα κοινές. Αυτές είναι b = 10, b = e (η άρρητη μαθηματική σταθερά ≈ 2.71828), και b = 2. Στη μαθηματική ανάλυση, ο λογάριθμος με βάση το e είναι διαδεδομένος εξαιτίας των ιδιαίτερων αναλυτικών ιδιοτήτων του που εξηγούνται παρακάτω. Από την άλλη, οι λογάριθμοι με βάση το 10 είναι εύκολοι στη χρήση για υπολογισμούς στο χέρι στο δεκαδικό σύστημα:[5]
Έτσι, ο log10(x) σχετίζεται με τον αριθμό των δεκαδικών ψηφίων ενός θετικού ακεραίου x: ο αριθμός των ψηφίων είναι ο μικρότερος ακέραιος που είναι αμέσως μεγαλύτερος από τον log10(x).[6] Για παράδειγμα, log10(1430) ισούται περίπου με 3,15. Ο επόμενος ακέραιος είναι το 4, το οποίο είναι ο αριθμός των ψηφίων του 1430. Ο λογάριθμος με βάση το δύο χρησιμοποιείται στην επιστήμη των υπολογιστών, όπου το δυαδικό σύστημα χρησιμοποιείται σχεδόν αποκλειστικά.
Στον ακόλουθο πίνακα φαίνονται κοινοί συμβολισμοί για τους λογάριθμους ως προς αυτές τις βάσεις και τα πεδία στα οποία χρησιμοποιούνται. Σε πολλά γνωστικά πεδία γράφεται log(x) αντί για logb(x), όταν η βάση μπορεί να προσδιοριστεί από τα συμπεριεχόμενα. Εμφανίζεται επίσης ο συμβολισμός blog(x).[7] Η στήλη «συμβολισμός ISO» έχει τους συμβολισμούς που προτείνονται από τον Διεθνή Οργανισμό Τυποποίησης (ISO 31-11).[8]
| Βάση b | Όνομα του logb(x) | Συμβολισμός ISO | Άλλοι συμβολισμοί | Χρήση |
|---|---|---|---|---|
| 2 | δυαδικός λογάριθμος | lb(x)[9] | ld(x), log(x) (στην επιστήμη υπολογιστών), lg(x) |
επιστήμη υπολογιστών, πληροφορική |
| e | φυσικός λογάριθμος | ln(x)[σημ. 3] | log(x) (στα μαθηματικά και πολλές γλώσσες προγραμματισμού[σημ. 4]) |
μαθηματική ανάλυση, φυσική, χημεία, στατιστική, οικονομικά, και κάποια γνωστικά πεδία μηχανικών |
| 10 | κοινός λογάριθμος | lg(x) | log(x) (μηχανική, βιολογία, αστρονομία), |
διάφορα πεδία μηχανικής, λογαριθμικοί πίνακες, επιστημονικά κομπιουτεράκια |
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Πρόδρομοι[Επεξεργασία | επεξεργασία κώδικα]
Ο Ινδός μαθηματικός Βιρασένα εργάστηκε πάνω στην έννοια του ardhaccheda: ο αριθμός των φορών που ένας αριθμός της μορφής 2n μπορεί να διαιρεθεί. Για ακριβείς δυνάμεις του 2, αυτό είναι ο λογάριθμος με βάση το 2, ο οποίος είναι ακέραιος αριθμός, για άλλους αριθμόυς είναι αόριστος. Περιέγραψε σχέσεις όπως ο τύπος του γινομένου και εισήγαγε επίσης ακέραιους λογαρίθμους με βάση 3 (trakacheda) και 4 (caturthacheda).[13][14] Ο Μίχαελ Στίφελ δημοσίευσε το έργο Arithmetica integra το 1544 στη Νυρεμβέργη το οποίο περιέχει ένα πίνακα[15] ακεραίων και δυνάμεων του 2 οποίος θεωρείται πρώιμη εκδοχή ενός λογαριθμικού πίνακα.[16][17]
Από τον Νάπιερ στον Όιλερ[Επεξεργασία | επεξεργασία κώδικα]

Η μέθοδος των λογαρίθμων δόθηκε στη δημοσιότητα από τον Τζον Νάπιερ το 1614, σε ένα βιβλίο υπό τον τίτλο Mirifici Logarithmorum Canonis Descriptio (Περιγραφή του Θαυμαστού Κανόνα των Λογαρίθμων).[18] Ο Γιοστ Μπέργκι (Jost Bürgi) εφήυρε ανεξάρτητα του λογάριθμους αλλά τους δημοσίευσε έξι χρόνια μετά τον Νάπιερ.[19]
Με επαναλαμβανόμενες αφαιρέσεις ο Νάπιερ υπολόγισε το 107(1 − 10−7)L για L από 1 έως 100. Το αποτέλεσμα για L=100 είναι περίπου 0.99999 = 1 − 10−5. Ο Νάπιερ τότε υπολόγισε τα γινόμενα αυτών των αριθμών με το 107(1 − 10−5)L για L από 1 έως 50, και έπραξε αναλόγως για τα 0.9995 ≈ (1 − 10−5)20 και 0.99 ≈ 0.99520. Αυτοί οι υπολογισμοί, με τους οποίους ασχολήθηκε 20 χρόνια, του επέτρεψαν να βρίσκει, για οποιονδήποτε αριθμό N από 5 έως 10 εκατομμύρια, τον αριθμό L που λύνει την εξίσωση
Ο Νάπιερ ονόμασε αρχικά τον L «τεχνητό αριθμό», αλλά αργότερα εισήγαγε τον όρο «λογάριθμος» για να σημαίνει ένα αριθμό που δείχνει ένα λόγο, από τα ελληνικά αριθμός και λόγος. Σε σύγχρονο συμβολισμό, η σχέση με τους φυσικούς λογάριθμους είναι:[20]
όπου η προσέγγιση αντιστοιχεί στην παρατήρηση ότι
Η εφεύρεση διαδόθηκε γρήγορα και ευρέως γενόμενη δεκτή με επιδοκιμασία. Τα έργα των Μποναβεντούρα Καβαλιέρι (Ιταλία), Έντμουντ Γουίνγκειτ (Edmund Wingate, Γαλλία), Xue Fengzuo (Κίνα) και του Γιοχάνες Κέπλερ (Chilias logarithmorum, Γερμανία) βοήθησαν στη περεταίρω διάδοση της έννοιας του λογαρίθμου.[21]
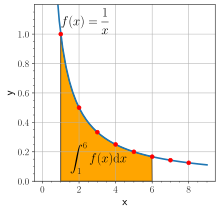
Το 1647 ο Grégoire de Saint-Vincent συσχέτισε τους λογάριθμους με τον τετραγωνισμό της υπερβολής, επισημαίνοντας ότι η επιφάνεια f(t) κάτω από την υπερβολή από x = 1 to x = t ικανοποιεί την σχέση
Ο φυσικός λογάριθμος περιγράφηκε για πρώτη φορά από τον Νίκολας Μερκάτορ στο έργο του Logarithmotechnia που δημοσιεύτηκε το 1668,[22] αν και ο δάσκαλος μαθηματικών John Speidell είχε ήδη από 1619 συνθέσει ένα πίνακα φυσικών λογαρίθμων.[23] Γύρω στο 1730, ο Λέοναρντ Όιλερ όρισε την εκθετική συνάρτηση και τον φυσικό λογάριθμο ως
Ο Όιλερ έδειξε επίσης ότι οι δύο συναρτήσεις είναι αντίστροφες η μία της άλλης.[24][25][26]
Λογαριθμικοί πίνακες, λογαριθμικοί κανόνες και ιστορικές εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]

Απλοποιώντας δύκολους υπολογισμούς, οι λογάριθμοι συνέβαλαν στην πρόοδο της επιστήμης, και ειδικότερα της αστρονομίας. Ήταν κρίσιμοι για την προόδο στην τοπογραφία, την αστρονομική ναυτιλία και άλλα πεδία. Ο Πιέρ Σιμόν Λαπλάς ονόμασε του λογάριθμους
ένα θαυμαστό κατασκεύασμα το οποίο, μειώνοντας σε λίγες μέρες τον χρόνο δουλειάς πολλών μηνών, διπλασιάζει την ζωή του αστρονόμου και τον γλυτώνει από τα λάθη και την αηδία που είναι αχώριστα κομμάτια των μεγάλων υπολογισμών.[27]
Ένα κομβικό εργαλείο που επέτρεψε στην πράξη την χρήση των λογαρίθμων πριν τα κομπιουτεράκια και τους υπολογιστές ήταν ο πίνακας λογαρίθμων.[28] Ο πρώτος τέτοιος πίνακας συντέθηκε από τον Χένρι Μπριγκς το 1617, αμέσως μετά την εφεύρεση του Νάπιερ. Εν συνεχεία γράφτηκαν πίνακες με ευρύτερο πεδίο και μεγαλύτερη ακρίβεια. Αυτοί οι πίνακες είχαν τιμές του logb(x) και του bx για κάθε x σε ένα συγκεκριμένο εύρος, με συγκεκριμένη ακρίβεια, και συγκεκριμένη βάση b (συνήθως b = 10). Για παράδειγμα, ο πρώτος πίνακας του Μπριγκς περιείχε τους κοινούς λογάριθμους όλως των ακεραίων στο εύρος 1–1000, με ακρίβεια 8 ψηφίων. Καθώς η συνάρτηση f(x) = bx είναι η αντίστροφη του logb(x), ονομάστηκε αντιλογάριθμος.[29] Το γινόμενο και το πηλίκο δύο θετικών αριθμών c και d υπολογίζονταν ως το άθρισμα και η διαφορά των λογαρίθμων τους. Το γινόμενο cd ή το πηλίκο c/d βρίσκονταν ψάχνοντας το άθρισμα ή την διαφορά, επίσης από τον ίδιο πίνακα:
και
Για υπολογισμούς στο χέρι που απαιτούν κάποια ακρίβεια, το ψάξιμο των δύο λογαρίθμων στον πίνακα, ο υπολογισμός του αθρίσματος ή της διαφοράς, και η εύρεση του αντιλογαρίθμου είναι πολύ γρηγορότερη υπόθεση από το να εκτελεστεί ο παλλαπλασιασμός με πρώιμες μεθόδους όπως η προσθαφαίρεση, η οποία βασίζεται σε τριγωνομετρικές ταυτότητες. Οι υπολογισμοί δυνάμεων και ριζών ανάγονται σε πολλαπλασιασμούς και διαιρέσεις όπως
και
Πολλοί λογαριθμικοί πίνακες δίνουν λογάριθμους παρέχοντας ξεχωριστά το ακέραιο λογαριθμικό (χαρακτηριστικό) και το δεκαδικό λογαριθμικό (mantissa) μέρος του x.[30] Το χαρακτηριστικό του 10 · x είναι ένα συν το χαρακτηριστικό του x, ενώ το δεκαδικό μέρος είναι το ίδιο. Αυτό επεκτείνει το εύρος των λογαριθμικών πινάκων: δεδομένου ενός πίνακα που έχει τα log10(x) για ακέραιους από 1 έως 1000, ο λογάριθμος του 3542 προσεγγίζεται ως
Μία ακόμα σημαντική εφαρμογή ήταν ο λογαριθμικός κανόνας, ένα ζεύγος λογαριθμικώς χωρισμένων κλιμάκων όπως φαίνεται εδώ:

Η μή κινούμενη λογαριθμική κλίμακα, ο κανόνας του Gunter, εφευρέθηκε λίγο μετά την εφεύρεση του Νάπιερ. Ο William Oughtred τον χρησιμοποίησε για να κατασκευάσει τον κινούμενο κανόνα, ένα ζεύγος λογαριθμικών κλιμάκων που κινούνται η μία ως προς την άλλη. Οι αριθμοί τοποθετούνται σε αποστάσεις ανάλογες των διαφορών των λογαρίθμων τους. Κινώντας τη άνω κλίμακα προκύπτει μηχανική άθροιση των λογαρίθμων. Για παράδειγμα, προσθέτωντας την απόσταση από το 1 στο 2 στην κάτω κλίμακα με την απόσταση από το 1 στο 3 στην πάνω κλίμακα δίνει το γινόμενο 6, το οποίο διαβάζεται στο κάτω μέρος. Ο λογαριθμικός κανόνας ήταν απαραίτητο εργαλείο υπολογισμών για μηχανικούς και επιστήμονες μέχρι την δεκαετία του 1970, επειδή επιτρέπει, με το κόστος της μικρότερης ακρίβειας, πολύ ταχύτερους υπολογισμούς από ότι τεχνικές με βάση πίνακες.[24]
Αναλυτικές ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Η βαθύτερη μελέτη των λογαρίθμων απαιτεί την έννοια της συνάρτησης. Η συνάρτηση είναι ένας κανόνας ο οποίος, δεδομένου ενός αριθμού, παράγει ένα άλλο μοναδικό αριθμό.[31] Ένα παράδειγμα είναι η συνάρτηση που παράγει την x-οστή δύναμη b από οποιονδήποτε πραγματικό αριθμό x, όπου η βάση b είναι σταθερός αριθμός. Αυτή η συνάρτηση γράφεται
Λογαριθμική συνάρτηση[Επεξεργασία | επεξεργασία κώδικα]
Για να οριστεί ο λογάριθμος, είναι αναγκαίο να δειχτεί ότι η εξίσωση
έχει λύση x και ότι αυτή η λύση είναι μοναδική, υπό τον όρο ότι το y είναι θετικό και το b είναι θετικό και μη ίσο με τη μονάδα. Η απόδειξη αυτού απαιτεί το θεώρημα της ενδιάμεσης τιμής από τον στοιχειώδη λογισμό.[32] Σύμφωνα με αυτό το θεώρημα μία συνεχής συνάρτηση η οποία έχει τιμές m και n έχει επίσης τιμές μεταξύ των m και n. Μία συνάρτηση είναι συνεχής όταν δεν παρουσιάζει άλματα στη γραφική της παράσταση.
Αυτή η ιδιότητα μπορεί να δειχτεί ότι ισχύει για τη συνάρτηση f(x) = bx. Επειδή η f παίρνει τυχαία μεγάλες και μικρές θετικές τιμές, οποιοσδήποτε αριθμός y > 0 βρίσκεται μεταξύ του f(x0) και f(x1) για κατάλληλα x0 και x1. Συνεπώς, το θεώρημα ενδιάμεσης τιμής διασφαλίζει ότι η εξίσωση f(x) = y έχει λύση. Επιπροσθέτως, υπάρχει μόνο μία λύση για αυτή την εξίσωση, επειδή η f είναι γνησίως αύξουσα (για b > 1), ή γνησίως φθίνουσα (για 0 < b < 1).[33]
Η μοναδική λύση x είναι ο λογάριθμος του y με βάση b, logb(y). Η συνάρτηση η οποία αποδίδει τιμές στο y αποκαλείται λογαριθμική συνάρτηση ή συνάρτηση λογαρίθμου (ή απλά λογάριθμος).
Αντίστροφη συνάρτηση[Επεξεργασία | επεξεργασία κώδικα]

Σύμφωνα με τον τύπο του λογαρίθμου μίας δύναμη, για οποιονδήποτε αριθμό x,
Δηλαδή, παίρνοντας την x-στή δύναμη του b και έπειτα τον λογάριθμο με βάση b, το αποτέλεσμα είναι x. Αντιστρόφως, δεδομένου ενός θετικού αριθμού y, ο τύπος
δηλώνει ότι παίρνοντας τον λογάριθμο ενός αριθμό ώς προς b και μετά υψώνοντας την βάση στο αποτέλεσμα, προκύπτει ο ίδιος ο αριθμός. Κατα συνέπεια, οι δύο πιθανοί τρόποι σύνθεσης λογαρίθμων και ύψωσης σε δύναμη έχουν ως αποτέλεσμα των αρχικό αριθμό. Συνεπώς, ο λογάριθμος με βάση b είναι η αντίστροφη συνάρτηση της f(x) = bx.[34]
Οι αντίστροφες συναρτήσεις έχουν στενή σχέση με τις αρχικές συναρτήσεις. Οι γραφικές τους παραστάσεις μπορούν να βρεθούν, η μία από την άλλη, αλλάζοντας τις συντεταγμένες x με τις y (ή με ανάκλαση στην διαγώνια ευθεία x = y), όπως φαίνεται δεξιά: ένα σημείο (t, u = bt) στη γραφική παράσταση της f έχει τιμή (u, t = logbu) στο γράφημα του λογαρίθμου και αντίστροφα. Κατά συνέπεια, logb(x) τείνει στο άπειρο καθώς το x τείνει στο άπειρο, δεδομένου ότι το b είναι μεγαλύτερο από ένα. Σε αυτή την περίπτωση η logb(x) ειναι γνησίως αύξουσα. Για b < 1, η logb(x) τείνει στο μείον άπειρο αντίστοιχα. Όταν το x τείνει στο μηδέν, η logb(x) τείνει στο μείον άπειρο για b > 1 (συν άπειρο για b < 1, αντίστοιχα).
Παράγωγος και αντιπαράγωγος[Επεξεργασία | επεξεργασία κώδικα]

Οι αναλυτικές ιδιότητες των συναρτήσεων κληροδοτούνται στις αντίστροφές τους.[32] Έτσι, καθώς η f(x) = bx είναι συνεχής και παραγωγίσιμη συνάρτηση, έτσι είναι και η logb(y). Χοντρικά, μία συνεχής συνάρτηση είναι παραγωγίσιμη αν η γραφική της παράσταση δεν έχει «γωνίες». Επιπροσθέτως, καθώς η παράγωγος της f(x) ισούται με ln(b)bx σύμφωνα με τις ιδιότητες της εκθετικής συνάρτησης, σύμφωνα με τον κανόνα παραγώγισης σύνθετης συνάρτησης η παράγωγος του logb(x) δίνεται από τον τύπο[33][35]
Τουτέστιν, η κλίση της εφαπτομένης που εφάπτεται στη γραφική παράσταση του λογαρίθμου με βάση b στο σημείο (x, logb(x)) ισούται με 1/(x ln(b)). Πιο συγκεκριμένα, η παράγωγος του ln(x) είναι 1/x, το οποίο υποδηλώνει ότι η αντιπαράγωγος του 1/x είναι ln(x) + C. Η παράγωγος με γενικευμένο όρισμα f(x) είναι
Το πηλίκο στο δεξιό μέρος αποκαλείται λογαριθμική παράγωγος της f. Υπολογίζοντας το f'(x) μέσω της παραγώγου ln(f(x)) είναι γνωστό ως λογαριθμική παραγώγιση.[36] The antiderivative of the natural logarithm ln(x) is:[37]
Σχετικοί τύποι, όπως οι αντιπαράγωγοι λογαρίθμων με άλλες βάσεις μπορούν να προκύψουν από αυτή την εξίσωση με αλλαγή βάσεων.[38]
Ολοκληρωτική αναπαράσταση του φυσικού λογαρίθμου[Επεξεργασία | επεξεργασία κώδικα]

Ο φυσικός λογάριθμος του t είναι ίσος με το ολοκλήρωμα του 1/x dx από το 1 στο t:
Με άλλα λόγια, το ln(t) ισούται με την επιφάνεια μεταξύ του άξονα των x και την γραφική παράσταση της συνάρτησης 1/x, επό το σημείο x = 1 έως το x = t (σχήμα στα δεξιά). Αυτό είναι συνέπεια του θεμελιώδους θεωρήματος του λογισμού και του γεγονότος ότι η παράγωγος του ln(x) είναι 1/x. Το δεξί μέρος της εξίσωσης μπορεί να χρησιμοποιηθεί και ως ορισμός του φυσικού λογαρίθμου. Τύποι για γινόμενα και δυνάμεις λογαρίθμων μπορούν να προκύψουν από αυτόν τον ορισμό.[39] Για παράδειγμα, ο τύπος για το γινόμενο ln(tu) = ln(t) + ln(u) μπορεί να προκύψει:
Η εξίσωση (1) χωρίζει το ολοκλήρωμα σε δύο μέρη, ενώ στην εξίσωση (2) γίνεται αλλαγή μεταβλητής (w = x/t).[σημ. 5] Στο σχήμα παρακάτω, ο χωρισμός αντιστοιχεί στη διαίρεση της επιφάνειας στο κίτρινο και το μπλε τμήμα. Μειώνοντας την οριζόντια και την κατακόρυφη κλίμακα κατά τον ίδιο παράγοντα t δεν αλλάζει το μέγεθος. Μετακινώντας την κατάλληλα, η επιφάνεια ταιριάζει ξανά στη γραφική παράσταση της συνάρτησης f(x) = 1/x. Κατά συνέπεια, η αριστερή μπλε επιφάνεια η οποία είναι το ολοκλήρωμα της f(x) από το t στο tu είναι η ίδια με το ολοκλήρωμα από το 1 στο u.

Ο τύπος της δύναμης ln(tr) = r ln(t) μπορεί να προκύψει με παρόμοιο τρόπο:
Η δεύτερη εξίσωση κάνει χρήση μίας αλλαγής μεταβλητών (ολοκλήρωση με αντικατάσταση),w := x1/r. Το άθροισμα των αντίστροφων των φυσικών αριθμών,
ονομάζεται αρμονική σειρά. Είναι στενά συνδεμένη με τον φυσικό λογάριθμο: καθώς το n τείνει στο άπειρο, η διαφορά,
συγκλίνει σε ένα αριθμό γνωστό ως σταθερά Euler-Mascheroni. Αυτή η σχέση βοηθά στην ανάλυση της απόδοσης αλγορίθμων όπως ο quicksort.[40]
Υπολογισμός[Επεξεργασία | επεξεργασία κώδικα]
Οι λογάριθμοι είναι εύκολο να υπολογιστούν σε κάποιες περιπτώσεις, όπως για παράδειγμα log10(10,000) = 4. Εν γένει μπορούν να υπολογιστούν με χρήση δυναμοσειρών ή του αριθμητικού-γεωμετρικού μέσου ή να παρθούν από προϋπολογισμένο λογαριθμικό πίνακα με δεδομένη ακρίβεια.[41][42] Επιπλέον, ο αλγόριθμος δυαδικού λογαρίθμου υπολογίζει το lb(x) αναδρομικά με βάση επαναλαμβανόμενους τετραγωνισμούς του x, κάνοντας χρήση της σχέσης
Η Μέθοδος Newton, μία επαναληπτική μέθοδος προσεγγιστικής επίλυσης εξισώσεων, μπορεί επίσης να χρησιμοποιηθεί για τον υπολογισμό του λογάριθμου, επειδή η αντίστροφη συνάρτηση, η εκθετική συνάρτηση, μπορεί να υπολογιστεί αποδοτικά.[43]
Από θεωρητική άποψη, σύμφωνα με το θεώρημα Gelfond-Schneider, οι λογάριθμοι συνήθως παίρνουν «δύσκολες» τιμές. Η τυπική διατύπωση βασίζεται στην έννοια των αλγεβρικών αριθμών, οι οποίοι περιλαμβάνουν όλους τους ρητούς αριθμούς, αλλά και αριθμούς όπως η τετραγωνική ρίζα του 2 ή ο
Οι μιγαδικοί αριθμοί οι οποίοι δεν είναι αλγεβρικοί αποκαλούνται υπερβατικοί αριθμοί,[44] για παράδειγμα το π και το e είναι τέτοιοι αριθμοί. Σχεδόν όλοι οι μιγαδικοί αριθμοί είναι υπερβατικοί. Με βάση αυτά, σύμφωνα με το θεώρημα Gelfond–Scheider δεδομένων δύο αλγεβρικών αριθμών a και b, ο logb(a) είναι είτε υπερβατικός είτε ρητός αριθμός p / q (στην οποία περίπτωση aq = bp, έτσι a και b είχαν εξαρχής στενή σχέση).[45]
Δυναμοσειρές[Επεξεργασία | επεξεργασία κώδικα]
- Σειρά Taylor

Για οποιονδήποτε πραγματικό αριθμό z που ικανοποιεί το 0 < z < 2, ισχύει ο ακόλουθος τύπος:[σημ. 6][46]
Το οποίο είναι συνομογραφία της διατύπωσης ότι ο ln(z) μπορεί να προσεγγιστεί με ολοένα μεγαλύτερη ακρίβεια καθώς προσθέτουμε διαδοχικά όρους από την ακολουθία:
Για παράδειγμα, η τρίτη προσέγγιση με z = 1.5 δίνει 0.4167, περίπου 0.011 παραπάνω από το ln(1.5) = 0.405465. Έτσι το ln(z) μπορεί να προσεγγιστεί με οποιαδήποτε ακρίβεια, δεδομένου ότι ο αριθμός των προσθετέων είναι μεγάλος αρκετά. Στον στοιχειώδη λογισμό, το ln(z) συνεπώς αποκαλείται το όριο αυτής της σειράς αθρισμάτων. Είναι η σειρά Taylor του φυσικού λογάριθμου στο z = 1.
- Πιο αποδοτικές σειρές
Μια άλλη σειρά είναι:
για μιγαδικούς αριθμούς z με θετικό πραγματικό μέρος.[46] Χρησιμοποιόντας τον συμβολισμό Σίγμα μπορεί να γραφτεί και ως
Αυτή η σειρά μπορεί να προκύψει από την παραπάνω σειρά Taylor. Συγκλίνει πιο γρήγορα από την σειρά Taylor, ειδικά αν το z είναι κοντά στο 1. Για παράδειγμα για z = 1.5, ο πρώτοι τρεις όροι της δεύτερης σειράς προσεγγίζουν το ln(1.5) με σφάλμα περίπου 3×10−6. Αυτή η γρήγορη σύγκλιση για z κοντά στο 1 μπορεί να χρησιμοποιηθεί με τον ακόλουθο τρόπο: δεδομένης μίας μικρής ακρίβειας προσέγγισης y ≈ ln(z) και θέτοντας
ο λογάριθμος του z είναι:
Όσο καλύτερη είναι η αρχική προσέγγιση του y, τόσο πιο κοντά στο 1 είναι το A, έτσι ο λογάριθμός του μπορεί να υπολογιστεί αποδοτικά. Το A μπορεί να υπολογιστεί χρησιμοποιώντας την εκθετική σειρά, η οποία συγκλίνει γρήγορα υπό τον όρο ότι το y δεν είναι πολύ μεγάλο. Ο υπολογισμός λογάριθμων μεγαλύτερων z μπορεί να αναχθεί σε μικρότερες τιμές του z γράφοντας z = a · 10b, έτσι ώστε ln(z) = ln(a) + b · ln(10).
Με παρόμοια μέθοδος μπορεί να χρησιμοποιηθεί για τον υπολογισμό λογαρίθμων ακεραίων. Από την παραπάνω σειρά, προκύπτει ότι:
Αν ο λογάριθμος ενός μεγάλου ακεραίου n είναι γνωστός, τότε αυτή η σειρά μπορεί να αποδώσει μία ταχέως συγκλίνουσα σειρά για το log(n+1).
Προσέγγιση με τον αριθμητικό-γεωμετρικό μέσο[Επεξεργασία | επεξεργασία κώδικα]
Ο αριθμητικός-γεωμετρικός μέσος αποδίδει υψηλής ακρίβειας προσεγγίσεις του φυσικού λογαρίθμου. Το ln(x) προσεγγίζεται με ακρίβεια 2−p (ή p δυαδικών ψηφίων) από τον ακόλουθο τύπο του Καρλ Φρίντριχ Γκάους:[47][48]
Εδώ το M είναι ο αριθμητικός-γεωμετρικός μέσος. υπολογίζεται από τον επαναληπτικό υπολογισμό του μέσου (αριθμητικός μέσος) και της τετραγωνικής ρίζας του γινομένου των δύο αριθμών (γεωμετρικός μέσος). Επιπλέον, το m επιλέγεται ώστε
Και ο αριθμητικός-γεωμετρικός μέσος και οι σταθερές π και ln(2) μπορούν να υπολογιστούν από ταχέως συγκλίνουσες σειρές.
Εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]

Οι λογάριθμοι έχουν πολλές εφαρμογές εντός και εκτός των μαθηματικών. Κάποιες χρήσεις τους έχουν σχέση με την έννοια της ανεξαρτησίας κλίμακας. Για παράδειγμα, κάθε τμήμα του όστρακου ενός ναυτίλου είναι σχεδόν αντίγραφο του επόμενου, κλιμακωμένο κατά ένα σταθερό παράγοντα. Έτσι δημιουργείται λογαριθμική σπείρα.[49] Ο νόμος του Benford για την κατανομή των πρώτων ψηφίων δεδομένων μπορεί επίσης να εξηγηθεί από την ανεξαρτησία κλίμακας.[50] Οι λογάριθμοι συνδέονται και με την αυτοομοιότητα. Για παράδειγμα, οι λογάριθμοι εμφανίζονται στην ανάλυση αλγορίθμων που λύνουν ένα πρόβλημα χωρίζοντάς το σε δύο παρόμοια μικρότερα προβλήματα κάνοντας επαλληλία στις λύσεις.[51] Οι διαστάσεις των αυτοόμοιων γεωμετρικών σχημάτων, δηλαδή τα σχήματα των οποίων τα μέρη μοιάζουν με το σύνολο βασίζονται επίσης σε λογάριθμους. Οι λογαριθμικές κλίμακες είναι χρήσιμες για την ποσοτικοποίηση των σχετικών αλλαγών μίας τιμής αντί για τις απόλυτες διαφορές. Επιπροσθέτως, επειδή η λογαριθμική συνάρτηση log(x) αυξάνεται πολύ αργά για μεγάλα x, οι λογαριθμικές κλίμακες χρησιμοποιούνται για την συμπίεση μεγάλης κλίμακας επιστημονικών δεδομένων. Οι λογάριθμοι εμφανίζονται και σε πάρα πολλούς επιστημονικούς τύπους, όπως για παράδειγμα η πυραυλική εξίσωση Tsiolkovsky, η εξίσωση Fenske και η εξίσωση Nernst.
Λογαριθμική κλίμακα[Επεξεργασία | επεξεργασία κώδικα]

Οι επιστημονικές ποσότητες συχνά εκφράζονται ως λογάριθμοι άλλων ποσοτήτων, χρησιμοποιώντας μία λογαριθμική κλίμακα. Για παράδειγμα, το ντεσιμπέλ είναι λογαριθμική μονάδα μέτρησης. Βασίζεται στον κοινό λογάριθμο λόγων—10 φορές ο κοινός λογάριθμος ενός λόγου ισχύος ή 20 φορές ο κοινός λογάριθμος του λόγου διαφοράς δυναμικού. Χρησιμοποιείται για να ποσοτικοποιήσει την απώλεια τάσης στη μετάδοση ηλεκτρικών σημάτων,[52] για να περιγράψει επίπεδα ισχύος των ήχων στην ακουστική,[53] και την απορρόφηση φωτός στα πεδία της φασματοσκοπίας και της οπτικής. Ο λόγος σήματος προς θόρυβο που περιγράφει την ποσότητα του ανεπιθύμητου θορύβου σε σχέση με ένα σήμα επίσης μετριέται σε ντεσιμπέλ.[54] Κατά παρόμοιο τρόπο, ο λόγος αιχμής σήματος προς θόρυβο χρησιμοποιείται συχνά για την αποτίμηση της ποιότητας του ήχου και των μεθόδων συμπίεσης εικόνας κάνοντας χρήση του λογάριθμου.[55]
Η ισχύς ενός σεισμού μετριέται λαμβάνοντας τον κοινό λογάριθμο της ενέργειας που ελευθερώνεται κατά την δόνηση. Αυτό χρησιμοποιείται στην κλίμακα μεγέθους ροπής ή την κλίμακα Ρίχτερ. Για παράδειγμα ένας σεισμός μεγέθους 5.0 απελευθερώνει 10 φορές και ένας μεγέθους 6.0 100 φορές την ενέργεια ενός σεισμού μεγέθους 4.0.[56] Μία άλλη λογαριθμική κλίμακα είναι το φαινόμενο μέγεθος. Μετράει την λαμπρότητα των αστέρων λογαριθμικά.[57] Ακόμα ένα παράδειγμα είναι το pH στη χημεία, το pH είναι ο αρνητικός κοινός λογάριθμος της ενεργότητας των ιόντων υδροξωνίου (η μορφή που παίρουν τα ιόντα υδρογόνου H+ στο νερό).[58] Η ενεργότητα των ιόντων υδροξωνίου στο ουδέτερο νερό είναι 10−7 mol·L−1, έτσι το pH είναι 7. Το ξύδι τυπικά έχει pH περίπου 3. Η διαφορά 4 με το ουδέτερο νερό αντιστοιχεί σε διαφορά 104 στη ενεργότητα, δηλαδή η ενεργότητα των ιόντων υδροξωνίου στο ξύδι είναι περίπου 10−3 mol·L−1.
Τα ημιλογαριθμικά γραφήματα κάνουν χρήση της λογαριθμικής κλίμακας για οπτικοποίηση, όπου ένας άξονας, τυπικά ο κατακόρυφος, είναι σε λογαριθμική κλίμακα. Για παράδειγμα το γράφημα στα αριστερά, συμπιέζει την μεγάλη αύξηση από το 1 εκατομμύριο στο 1 τρισεκατομμύριο στον ίδιο χώρο (στον κατακόρυφο άξονα) με την αύξηση από το 1 στο 1 εκατομμύριο. Σε τέτοιου είδους γραφήματα, οι εκθετικές συναρτήσεις του τύπου f(x) = a · bx εμφανίζονται ως ευθείες γραμμές με κλίση ανάλογη του b. Σε γραφήματα με λογαριθμική κλίμακα και στους δύο άξονες, συναρτήσεις του τύπου f(x) = a · xk αναπαρίστανται ως ευθείες με κλίση ανάλογη του εκθέτη k. Αυτό έχει εφαρμογή στην οπτικοποίηση και ανάλυση εκθετικών νόμων.[59]
Ψυχολογία[Επεξεργασία | επεξεργασία κώδικα]
Οι λογάριθμοι εμφανίζονται σε διάφορους νόμους που περιγράφουν την ανθρώπινη αντίληψη:[60][61] Ο νόμος του Χικ προτείνει λογαριθμική σχέση μεταξύ του χρόνου που χρειάζεται ένα άτομο για την επιλογή μίας απόφασης και του αριθμού των επιλογών που έχει.[62] Ο νόμος του Φιτ προβλέπει ότι ο χρόνος που απαιτείται για ταχεία κίνηση σε μία περιοχή στόχο είναι λογαριθμική συνάρτηση της απόστασης και του μεγέθους του στόχου.[63] Στην ψυχοφυσική, ο νόμος Βέμπερ-Φέχνερ προτείνει λογαριθμική σχέση μεταξύ του ερεθίσματος και της αίσθησης όπως για παράδειγμα το πραγματικό και το φαινόμενο βάρος ενός αντικειμένου που κουβαλάει ένα άτομο.[64] (Αυτός ο «νόμος» ωστόσο είναι λιγότερο ακριβής από νεότερα μοντέλα όπως ο εκθετικός νόμος του Stevens.[65])
Ψυχολογικές μελέτες έχουν διαπιστώσει ότι μαθηματικώς ακαλλιέργητα άτομα τείνουν να εκτιμούν τις ποσότητες λογαριθμικά, δηλαδή τοποθετούν ένα αριθμό σε μία αβαθμονόμητη γραμμή στον λογάριθμό του, έτσι ώστε το 10 τοποθετείται τόσο κοντά στο 20 όσο το 100 στο 200. Η αύξηση της μαθηματικής κατανόησης μετατοπίζει αυτή την συμπεριφορά προς την γραμμική εκτίμμηση.[66][67]
Θεωρία πιθανοτήτων και στατιστική[Επεξεργασία | επεξεργασία κώδικα]


Οι λογάριθμοι εμφανίζονται και στην θεωρία πιθανοτήτων: σύμφωνα με τον νόμο των μεγάλων αριθμών, για ένα δίκαιο νόμισμα , καθώς ο αριθμός που ρίχνεται το νόμισμα τείνει στο άπειρο, η παρατηρούμενη αναλογία των «κεφαλών» τείνει στο μισό. Οι αυξομειώσεις αυτής της αναλογίας γύρω από το μισό περιγράφονται από τον νόμο του επαναλαμβανόμενου λογάριθμου.[68]
Οι λογάριθμοι εμφανίζονται επίσης στις λογαριθμοκανονικές κατανομές. Όταν ο λογάριθμος μίας τυχαίας μεταβλητής έχει κανονική κατανομή, τότε λέγεται ότι η μεταβλητική έχει λογαριθμοκανονική κατανομή.[69] Οι λογαριθμοκανονικές κατανομές εμφανίζονται σε πολλά πεδία, οπουδήποτε η μεταβλητή σχηματίζεται ως γινόμενο πολλών ανεξάρτητων θετικών τυχαίων μεταβλητών, όπως για παράδειγμα στη μελέτη της τύρβης.[70]
Οι λογάριθμοι χρησιμοποιούνται για την εκτίμηση μέγιστης πιθανοφάνειας παραμετρικών στατιστικών μοντέλων. Για ένα τέτοιο μοντέλο, η συνάρτηση πιθανοφάνειας (likelihood function) εξαρτάται από τουλάχιστον μία παράμετρο που χρειάζεται να εκτιμηθεί. Ένα μέγιστο για τη συνάρτηση πιθανοφάνειας εμφανίζεται στην ίδια παράμετρο-τιμή όπως και στο μέγιστο του λογάριθμου της πιθανοφάνειας (λογαριθμο-πιθανοφάνεια), επειδή ο λογάριθμος είναι αύξουσα συνάρτηση.Η λογαριθμο-πιθανοφάνεια είναι ευκολότερο να μεγιστοποιηθεί, ειδικότερα για τις πολλαπλασιασμένες πιθανοφάνεις ανεξάρτητων τυχαίων μεταβλητών.[71]
Ο νόμος του Benford περιγράφει την εμφάνιση ψηφίων σε πολλά σύνολα δεδομένων, όπως για παράδειγμα τα ύψη κτηρίων]]. Σύμφωνα με τον νόμο του Benford, η πιθανότητα το πρώτο ψηφίο (στο δεκαδικό σύστημα) ενός αντικειμένου στο δείγμα δεδομένων να είναι d (από 1 έως 9) ισούται με log10(d + 1) − log10(d), ανεξαρτήτως της μονάδας μέτρησης.[72] Συνεπώς, περίπου το 30% των δεδομένων αναμένεται να έχει πρώτο ψηφίο το 1, το 18% να ξεκινά με 2, κτλ. Οι εξεταστές λογιστικών βιβλίων εξετάζουν αποκλίσεις από τον νόμο του Benford ώστε να ανακαλύψουν λογιστικές απάτες.[73]
Υπολογιστική πολυπλοκότητα[Επεξεργασία | επεξεργασία κώδικα]
Η ανάλυση αλγορίθμων είναι κλάδος της επιστήμης υπολογιστών που μελετά την απόδοση αλγορίθμων.[74] Οι λογάριθμοι είναι πολύτιμοι για την περιγραφή αλγόριθμων οι οποίοι χωρίζουν ένα πρόβλημα σε μικρότερα, και έπειτα συνδυάζονται οι λύσει των υποπροβλημάτων.[75]
Για παράδειγμα, για την εύρεση ενός αριθμού σε ένα ταξινομημένο κατάλογο, ο αλγόριθμος δυαδικής αναζήτησης ελέγχει τη μεσαία καταχώρηση και προχωρά με τον μισό κατάλογο πριν ή μετά το μεσαίο αν ο αριθμός δεν έχει ακόμα βρεθεί. Αυτός ο αλγόριθμος απαιτεί, κατά μέσο όρο, log2(N) συγκρίσεις, όπου N είναι το μήκος του καταλόγου.[76] Παρομοίως, ο αλγόριθμος merge sort ταξινομεί ένα αταξινόμητο κατάλογο χωρίζοντάς τον στη μέση και ταξινομώντας πρώτα τα μισά πριν συνδυάσει τα αποτελέσματα. Οι αλγόριθμοι merge sort τυπικά απαιτούν χρόνο περίπου ανάλογο του N · log(N).[77] Η βάση του λογάριθμου δεν καθορίζεται εδώ επειδή το αποτέλεσμα αλλάζει μόνο κατά ένα σταθερό παράγοντα όταν χρησιμοποιείται άλλη βάση. Ένας σταθερός παράγοντας, συνήθως δεν λαμβάνεται υπόψη στην ανάλυση αλγορίθμων υπό το τυπικό μοντέλο ομοιόμορφου κόστους.[78]
Μία συνάρτηση f(x) λέγεται ότι αυξάνεται λογαριθμικά αν η f(x) είναι (ακριβώς ή προσεγγιστικά) ανάλογη του λογαρίθμου του x. (Οι βιολογικές περιγραφές της ανάπτυξης οργανισμών, ωστόσο, χρησιμοποιούν αυτό τον όρο για εκθετικές συναρτήσεις.[79]) Για παράδειγμα, οποιοσδήποτε φυσικός αριθμός N μπορεί να αναπαρασταθεί σε δυαδική μορφή σε όχι παραπάνω από log2(N) + 1 bit. Με άλλα λόγια, το ποσό της μνήμης που απαιτείται για την αποθήκευση του N αυξάνεται λογαριθμικά με το N.
Εντροπία και χάος[Επεξεργασία | επεξεργασία κώδικα]

Η εντροπία είναι χοντρικά μέτρο της αταξίας κάποιου συστήματος. Στην στατιστική θερμοδυναμική, η εντροπία S ενός φυσικού συστήματος ορίζεται ως
Το άθροισμα αφορά όλες τις πιθανές καταστάσεις i του υπό εξέταση συστήματος, όπως οι θέσεις των σωματιδίων αερίου σε ένα δοχείο. Επιπλέον, pi είναι η πιθανότητα ότι έχει επιτευχθεί η κατάσταση i και k είναι η σταθερά Boltzmann. Παρομοίως, η εντροπία στη θεωρία πληροφοριών μετράει την ποσότητα της πληροφορίας/ Αν ένας αποδέκτης μηνύματος αναμένει οποιοδήποτε από τα N πιθανά μηνύματα με την ίδια πιθανότητα, τότε η ποσότητα πληροφορίας που μεταβιβάζεται από οποιοδήποτε τέτοιο μήνυμα ποσοτικοποιείται ως log2(N) bit.[80]
Οι εκθέτες Lyapunov κάνουν χρήση λογαρίθμων για την μέτρηση της χαοτικότητας ενός δυναμικού συστήματος. Για παράδειγμα, για ένα σωματίδιο που κινείται σε ένα οβάλ τραπέζι μπιλιάρδου, ακόμα και μικρές αλλαγές των αρχικών συνθηκών έχουν αποτέλεσμα πολύ διαφορετικές τροχιές. Τέτοια συστήματα είναι χαοτικά κατά ντετερμινιστικό τρόπο επειδή μικρά σφάλματα μετρήσεων της αρχικής κατάστασης οδηγούν με προβλέψιμο τρόπο σε πολύ διαφορετικές τελικές καταστάσεις.[81] Τουλάχιστον ένας εκθέτης Λιαπούνοφ ενός ντετερμινιστικώς χαοτικού συστήματος είναι θετικός.
Φράκταλ[Επεξεργασία | επεξεργασία κώδικα]

Οι λογάριθμοι εμφανίζονται στους ορισμούς των διαστάσεων φράκταλ.[82] Τα φράκταλ είναι γεωμετρικά αντικείμενα με την ιδιότητα της αυτοομοιότητας: τα μικρότερα μέρη αναπαράγουν, τουλάχιστον χοντρικά, την πλήρη δομή. Το τρίγωνο Σιερπίνσκι (εικόνα) μπορεί να καλυφθεί από τρία αντίγραφα του εαυτού του, το καθένα με το μισό αρχικό μήκος. Αυτό έχει ως αποτέλεσμα η διάσταση Hausdorff της δομής να είναι log(3)/log(2) ≈ 1.58. Μία άλλη βασισμένη στους λογάριθμους έννοια διάσταση, αποκτάται με το μέτρημα των κουτιών που απαιτούνται για την κάληψη του υπό εξέταση φράκταλ (διάσταση Minkowski–Bouligand).
Μουσική[Επεξεργασία | επεξεργασία κώδικα]
Οι λογάριθμοι σχετίζονται με τους μουσικούς τόνους και τα μουσικά διαστήματα. Στον ισοσυγκερασμό, ο λόγος των συχνοτήτων εξαρτάται μόνο από το διάστημα μεταξύ δύο τόνων, όχι από την συγκεκριμένη συχνότητα ή το ύψος του κάθε τόνου. Για παράδειγμα, η νότα Λα έχει συχνότητα 440 Hz και η νότα Σι ύφεση έχει συχνότητα 466 Hz. Αντίστοιχα συμφωνεί ο λόγος των συχνοτήτων:
Συνεπώς, οι λογάριθμοι μπορούν να χρησιμοποιηθούν για την περιγραφή διαστημάτων: ένα διάστημα μετριέται σε ημιτόνια λαμβάνοντας τον λογάριθμο με βάση την δωδέκατη ρίζα του 2 (21/12) του λόγου των συχνοτήτων, ενώ με τον λογάριθμο με βάση την 1200ή ρίζα του 2 του λόγου των συχνοτήτων το διάστημα μετριέται σε σέντς (cents), εκατοστά του ημιτονίου. Το τελευταίο χρησιμοποιείται για ακριβέστερη κωδικοποίηση σε μή ισοσυγκερασμένα συστήματα.[83]
| Διάστημα (οι δύο τόνοι στα παραδείγματα παίζονται ταυτόχρονα) |
1/12 του τόνου play | Ημιτόνιο play | Ορθή μείζων τρίτη play | Μείζων τρίτη play | Τρίτωνας play | Οκτάβα play |
| Λόγος συχνοτήτων r | ||||||
| Αντίστοιχος αριθμός ημιτονίων |
||||||
| Αντίστοιχος αριθμός σεντς |
Θεωρία αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Οι φυσικοί λογάριθμοι συνδέονται στενά με την απαρίθμηση των πρώτων αριθμών (2, 3, 5, 7, 11, ...), σημαντικό θέμα στην θεωρία αριθμών. Για οποιονδήποτε ακέραιο x, η ποσότητα των πρώτων αριθμών που είναι μικρότεροι ή ίσοι με το x συμβολίζεται ως π(x). Σύμφωνα με το θεώρημα των πρώτων αριθμών, το π(x) δίνεται προσεγγιστικά από τον τύπο:
υπό την έννοια ότι ο λόγος του π(x) και αυτής της συνάρτησης προσεγγίζει το 1 όταν το x τείνει στο άπειρο.[84] Κατά συνέπεια, η πιθανότητα ένας τυχαίος αριθμός μεταξύ του 1 και του x να είναι πρώτος είναι αντιστρόφως ανάλογη με τον αριθμό των ψηφίων του x. Μία πολύ καλύτερη εκτίμηση του π(x) δίνεται από τo λογαριθμικό ολοκλήρωμα Li(x), το οποίο ορίζεται ως
Η υπόθεση Riemann, μία από τις παλαιότερες μη αποδεδειγμένες υποθέσεις, μπορεί να εκφραστεί ως σύγκριση των π(x) και Li(x).[85] Το θεώρημα Erdős–Kac που περιγράφει τον αριθμό των διακριτών πρώτων παραγόντων επίσης περιλαμβάνει τον φυσικό λογάριθμο.
Ο λογάριθμος του n παραγοντικού, n! = 1 · 2 · ... · n, δίνεται από τον τύπο
Αυτό μπορεί να χρησιμοποιηθεί για την παραγωγή του τύπου του Stirling, μίας προσέγγισης του n! για μεγάλους n.[86]
Γενικεύσεις[Επεξεργασία | επεξεργασία κώδικα]
Μιγαδικός λογάριθμος[Επεξεργασία | επεξεργασία κώδικα]

Οι μιγαδικοί αριθμοί a που επιλύουν την εξίσωση
ονομάζονται μιγαδικοί λογάριθμοι. Εδώ z είναι ένας μιγαδικός αριθμός. Ένας μιγαδικός αριθμός αναπαρίσταται κοινώς ως z = x + iy, όπου x και y είναι πραγματικοί αριθμοί και i είναι η φανταστική μονάδα. Ένας τέτοιος αριθμός μπορεί να παρασταθεί ως σημείο στο μιγαδικό επίπεδο, όπως φαίνεται στα δεξιά. Η πολική μορφή αναπαριστά ένα μη μηδενικό μιγαδικό αριθμό z χρησιμοποιώντας την απόλυτη τιμή του, ήτοι την απόσταση r από την αρχή των αξόνων, και μία γωνία μεταξύ του άξονα των x και της ευθείας που διέρχεται από την αρχή των αξόνων και τον z. Η γωνία καλείται όρισμα του z. Η απόλυτη τιμή r του z είναι
Το όρισμα φ δεν προσδιορίζεται μοναδικά από τον z: το φ' = φ + 2π είναι επίσης όρισμα του z επειδή προσθέτοντας 2π ακτίνια ή 360 μοίρες[σημ. 7] στο όρισμα φ αντιστοιχεί με αριστερόστροφη περιστροφή γύρω από την αρχή των αξόνων κατά γωνία 2π. Ο μιγαδικός αριθμός που προκύπτει έτσι είναι πάλι ο z, όπως φαίνεται στα δεξιά. Ωστόσο, μόνο ένα όρισμα φ ικανοποιεί τις −π < φ και φ ≤ π. Αυτό αποκαλείται κύριο ή πρωτεύον όρισμα και συμβολίζεται Arg(z), με κεφαλαίο Α.[87] (Μία εναλλακτική κανονικοποίηση είναι η 0 ≤ Arg(z) < 2π.[88])

Με την χρήση των τριγωνομετρικών συναρτήσεων του ημιτόνου και του συνημιτόνου, ή της μιγαδικής εκθετικής συνάρτησης, αντίστοιχα, τα r και φ είναι τέτοια ώστε ικανοποιούν ταυτότητες:[89]
Αυτό υποδηλώνει ότι η a-οστή δύναμη του e ισούται με το z, όπου
το φ είναι το κύριο όρισμα Arg(z) και n είναι τυχαίος ακέραιος. Οποιοσήποτε τέτοιος a καλείται μιγαδικός λογάριθμος του z. Υπάρχουν άπειροι μιγαδικοί λογάριθμοι ενός αριθμού, εν αντιθέσει με τον μοναδικά οριζόμενο πραγματικό λογάριθμο. Αν n = 0, το a καλείται κύρια τιμή του λογάριθμου και συμβολίζεται ως Log(z). Το κύριο όρισμα οποιουδήποτε θετικού πραγματικού αριθμού x είναι 0, συνεπώς το Log(x) είναι πραγματικός αριθμός και ισούται με τον πραγματικό (φυσικό) λογάριθμο. Ωστόσο οι παραπάνω τύποι για τους λογάριθμους γινομένων και δυνάμεων δεν γενικεύονται για την κύρια τιμή του μιγαδικού λογάριθμου.[90]
Η απεικόνιση δεξιά αναπαριστά το Log(z). Η ασυνέχεια, ήτοι το άλμα της απόχρωσης στο αρνητικό τμήμα του άξονα των x (πραγματικός άξονας), προκαλείται από την ασυνέχεια του κύριου ορίσματος. Ο τόπος αυτός ονομάζεται τομή διακλαδώσεως (branch cut). Αυτή η συμπεριφορά μπορεί να παρακαμφθεί μόνο αν εγκαταληφθεί ο περιορισμός στο εύρος του φ. Τότε το όρισμα του z και, κατά συνέπεια, ο οικείος λογάριθμος γίνονται πλειότιμες συναρτήσεις.
Αντίστροφες συναρτήσεις άλλων εκθετικών συναρτήσεων[Επεξεργασία | επεξεργασία κώδικα]
Η ύψωση σε δύναμη συναντάται σε πολλούς τομείς των μαθηματικών, ενώ η αντίστροφη αυτής συνάρτηση συχνά αποκαλείται λογάριθμος. Για παράδειγμα, ο λογάριθμος πίνακα είναι η πλειότιμη αντίστροφη συνάρτηση της δύναμης πίνακα.[91] Ένα άλλο παράδειγμα είναι η p-αδική λογαριθμική συνάρτηση, η αντίστροφη της p-αδικής εκθετικής συνάρτησης. Αμφότερες ορίζοναι με σειρά Taylor ανάλογη με την πραγματική περίπτωση.[92] Στο εννοιολογικό πλαίσιο της διαφορικής γεωμετρίας, η εκθετική απεικόνιση αντιστοιχίζει τον εφαπτόμενο χώρο σε ένα σημείο μίας πολλαπλότητας προς μία γειτονιά αυτού του σημείου. Η αντίστροφή της αποκαλείται επίσης λογαριθμική απεικόνιση.[93]
Στο εννοιολογικό πλαίσιο των πεπερασμένων ομάδων η ύψωση σε δύναμη συνίσταται στον επαναλαμβανόμενο πολλαπλασιασμό ενός στοιχείου b της ομάδας με τον εαυτό του. Ο διακριτός λογάριθμος είναι ο ακέραιος n, ο οποίος αποτελεί λύση της εξίσωσης
όπου x είναι στοιχείο της ομάδας. Η ύψωση σε δύναμη μπορεί να γίνει αποδοτικά, όμως ο υπολογισμός του διακριτού λογάριθμου πιστεύεται ότι είναι πολύ δύσκολος σε κάποιες ομάδες. Αυτή η ασυμμετρία έχει σημαντικές εφαρμογές στην κρυπτογραφία δημοσίου κλειδιού, όπως για παράδειγμα στην ανταλλαγή κλειδιών Diffie–Hellman, μία διαδικασία που επιτρέπει ασφαλείς ανταλλαγές κρυπτογραφικών κλειδιών σε μη ασφαλείς διαύλους πληροφοριών.[94] Ο λογάριθμος του Zech σχετίζεται μ ετον διακριτό λογάριθμο στην πολλαπλασιαστική ομάδα των μη μηδενικών στοιχείων ενός πεπερασμένου πεδίου.[95]
Άλλες λογαριθμοειδής συναρτήσεις είναι ο διπλός λογάριθμος ln(ln(x)), ο υπερ- ή υπερ-4-λογάριθμος (μια μικρή παραλλαγή του οποίου, στην επιστήμη των υπολογιστών αποκαλείται επαναλαμβανόμενος λογάριθμος (iterated logarithm), η συνάρτηση W του Lambert, και η logit. Είναι οι αντίστροφες συναρτήσεις αντίστοιχα της διπλής εκθετικής συνάρτησης, της επαναλαμβανόμενης ύψωσης σε δύναμη (tetration), της f(w) = wew,[96] και της λογιστικής συνάρτησης.[97]
Σχετικές έννοιες[Επεξεργασία | επεξεργασία κώδικα]
Από την οπτική των καθαρών μαθηματικών, η ταυτότητα log(cd) = log(c) + log(d) εκφράζει ισομορφισμό ομάδας μεταξύ θετικών πραγματικών υπό πολλαπλασιασμό και πραγματικών υπό πρόσθεση. Οι λογαριθμικές συναρτήσεις είναι οι μοναδικοί συνεχείς ισομορφισμοί μεταξύ αυτών των ομάδων.[98] Υπό αυτόν τον ισομορφισμό το μέτρο Haar dx στους πραγματικούς αντιστοιχεί στο μέτρο Haar dx/x στους θετικούς πραγματικούς.[99] Στην μιγαδική ανάλυση και την αλγεβρική γεωμετρία, οι διαφορικές μορφές της μορφής df/f είναι γνωστές ως μορφές με λογαριθμικό πόλο.[100]
Ο πολυλογάριθμος είναι η συνάρτηση που ορίζεται ως
Σχετίζεται με τον φυσικό λογάριθμο μέσω του τύπου Li1(z) = −ln(1 − z). Επιπλέον Lis(1) ισούται με την συνάρτηση ζήτα του Riemann ζ(s).[101]
Περαιτέρω ανάγνωση[Επεξεργασία | επεξεργασία κώδικα]
Ελληνικά άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- Η. Γεωργακάκος (1982). «Λογάριθμοι». Ευκλείδης Β΄ (1): 42-46. http://www.hms.gr/apothema/?s=sa&i=2735.
- Βισκαδουράκης Βασίλειος (1990). «Εκθετική και Λογαριθμική συνάρτηση. Μια "φυσική"... προσέγγιση». Ευκλείδης Β΄ (4). http://www.hms.gr/apothema/?s=sa&i=3402.
- Αθανασόπουλος Β. (1992). «Λογαριθμική συνάρτηση - Εξισώσεις - Ανισώσεις». Ευκλείδης Β΄ (3): 36-37. http://www.hms.gr/apothema/?s=sa&i=3505.
Ξενόγλωσσα άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- Mermin, N. David (Ιανουαρίου 1980). «Logarithms!». The American Mathematical Monthly 87 (1): 1–7. doi:. https://archive.org/details/sim_american-mathematical-monthly_1980-01_87_1/page/1.
- Porter, M. B. (Ιουνίου 1916). «The Derivative of the Logarithm». The American Mathematical Monthly 23 (6): 204–206. doi:. https://archive.org/details/sim_american-mathematical-monthly_1916-06_23_6/page/204.
- Clark, Kathleen M.; Montelle, Clemency (16 Ιουνίου 2010). Logarithms: The Early History of a Familiar Function. doi:.
- Ostler, Elliott (Μαΐου 2013). «Exploring Logarithms with a Ruler». The Mathematics Teacher 106 (9): 668–673. doi:. https://archive.org/details/sim_mathematics-teacher_2013-05_106_9/page/668.
- Bromwich, T. J. I’A. (Δεκεμβρίου 1928). «Elementary Treatment of Logarithms». The Mathematical Gazette 14 (197): 260–265. doi:. https://archive.org/details/sim_mathematical-gazette_1928-12_14_197/page/260.
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Για περισσότερες λεπτομέρειες, συμπεριλαμβανομένου του τύπου bm + n = bm · bn, δείτε δύναμη (μαθηματικά) ή [1] για μία στοιχειώδη έκθεση του θέματος.
- ↑ Οι περιορισμοί για το y και το b εξηγούνται στην ενότητα «Αναλυτικές ιδιότητες».
- ↑ Κάποιοι μαθηματικοί δεν εγκρίνουν αυτόν τον συμβολισμό. Στην αυτοβιογραφία του το 1985, ο Πολ Χάλμος άσκησε κριτική στον όπως τον θεωρούσε «παιδικό συμβολισμό ln», τον οποίο είπε ότι κανείς μαθηματικός δεν χρησιμοποίησε ποτέ.[10] Ο συμβολισμός εφευρέθηκε από τον Ίρβινγκ Στρίνγκαμ, μαθηματικό.[11][12]
- ↑ Για παράδειγμα C, Java, Haskell, and BASIC.
- ↑ Με αλλαγή μεταβλητής συνεπάγεται ότι συνεπώς .
- ↑ Η ίδια σειρά δίνει την κύρια τιμή του μιγαδικού λογάριθμου για μιγαδικούς αριθμούς z με |z − 1| < 1.
- ↑ Δείτε ακτίνιο για την μετατροπή μεταξύ 2π και 360 μοίρες.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Shirali, Shailesh (2002), A Primer on Logarithms, Hyderabad: Universities Press, ISBN 978-81-7371-414-6, ειδικότερα ενότητα 2
- ↑ Kate, S.K.; Bhapkar, H.R. (2009), Basics Of Mathematics, Pune: Technical Publications, ISBN 978-81-8431-755-8, κεφάλαιο 1
- ↑ Όλες οι δηλώσεις της ενότητας αυτής μπορούν να βρεθούν, για παράδειγμα, στα Shirali 2002, ενότητα 4, Downing 2003, σελ. 275, ή Bhapkar 2009, σελ. 1-1.
- ↑ Bernstein, Stephen; Bernstein, Ruth (1999), Schaum's outline of theory and problems of elements of statistics. I, Descriptive statistics and probability, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-005023-5, https://archive.org/details/schaumsoutlineof00bern, σ. 21
- ↑ Downing, Douglas (2003), Algebra the Easy Way, Barron's Educational Series, Hauppauge, N.Y.: Barron's, ISBN 978-0-7641-1972-9, https://archive.org/details/algebraeasyway00down_0, κεφάλαιο 17, σ. 275
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, σ. 20
- ↑ (Γερμανικά) Franz Embacher; Petra Oberhuemer, Mathematisches Lexikon, mathe online: für Schule, Fachhochschule, Universität unde Selbststudium, http://www.mathe-online.at/mathint/lexikon/l.html, ανακτήθηκε στις 22/03/2011
- ↑ B. N. Taylor (1995), Guide for the Use of the International System of Units (SI), US Department of Commerce, http://physics.nist.gov/Pubs/SP811/sec10.html#10.1.2, ανακτήθηκε στις 2007-08-27
- ↑ Gullberg, Jan (1997), Mathematics: from the birth of numbers., New York: W. W. Norton & Co, ISBN 978-0-393-04002-9
- ↑ Paul Halmos (1985), I Want to Be a Mathematician: An Automathography, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96078-4
- ↑ Irving Stringham (1893), Uniplanar algebra: being part I of a propædeutic to the higher mathematical analysis, The Berkeley Press, σελ. xiii, http://books.google.com/?id=hPEKAQAAIAAJ&pg=PR13&dq=%22Irving+Stringham%22+In-natural-logarithm&q=
- ↑ Roy S. Freedman (2006), Introduction to Financial Technology, Amsterdam: Academic Press, σελ. 59, ISBN 978-0-12-370478-8, http://books.google.com/?id=APJ7QeR_XPkC&pg=PA59&dq=%22Irving+Stringham%22+logarithm+ln&q=%22Irving%20Stringham%22%20logarithm%20ln
- ↑ Gupta, R. C. (2000), «History of Mathematics in India», στο: Hoiberg, Dale; Ramchandani, επιμ., Students' Britannica India: Select essays, New Delhi: Popular Prakashan, σελ. 329, http://books.google.co.uk/books?id=-xzljvnQ1vAC&pg=PA329&lpg=PA329&dq=Virasena+logarithm&source=bl&ots=BeVpLXxdRS&sig=_h6VUF3QzNxCocVgpilvefyvxlo&hl=en&ei=W0xUTLyPD4n-4AatvaGnBQ&sa=X&oi=book_result&ct=result&resnum=2&ved=0CBgQ6AEwATgK#v=onepage&q=Virasena%20logarithm&f=false
- ↑ Dr. Hiralal Jain, επιμ.. (1996), THE SHATKHANDAGAMA OF PUSHPADANTA AND BHOOTABAL (3rd έκδοση), Solapur: Jain Samskriti Samrakshaka Sangha, http://www.jainworld.com/JWHindi/Books/shatkhandagama-4/02.htm, ανακτήθηκε στις 2011-10-10, part 3-4-5, book 4
- ↑ Stifelio, Michaele (1544), Arithmetica Integra, London: Iohan Petreium, http://books.google.com/books?id=fndPsRv08R0C&pg=RA1-PT419
- ↑ Bukhshtab, A.A.; Pechaev, V.I. (2001), «Arithmetic», στο: Hazewinkel, Michiel, επιμ., Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/A/a013260.htm
- ↑ Vivian Shaw Groza and Susanne M. Shelley (1972), Precalculus mathematics, New York: Holt, Rinehart and Winston, σελ. 182, ISBN 978-0-03-077670-0, http://books.google.com/?id=yM_lSq1eJv8C&pg=PA182&dq=%22arithmetica+integra%22+logarithm&q=stifel
- ↑ Ernest William Hobson (1914), John Napier and the invention of logarithms, 1614, Cambridge: The University Press
- ↑ Boyer 1991, Κεφάλαιο 14, ενότητα "Jobst Bürgi"
- ↑ William Harrison De Puy (1893), The Encyclopædia Britannica: a dictionary of arts, sciences, and general literature ; the R.S. Peale reprint,, 17 (9th έκδοση), Werner Co., σελ. 179, http://babel.hathitrust.org/cgi/pt?seq=7&view=image&size=100&id=nyp.33433082033444&u=1&num=179
- ↑ Maor, Eli (2009), E: The Story of a Number, Princeton University Press, ISBN 978-0-691-14134-3, ενότητα 2
- ↑ J. J. O'Connor; E. F. Robertson (2001-09), The number e, The MacTutor History of Mathematics archive, http://www-history.mcs.st-and.ac.uk/HistTopics/e.html, ανακτήθηκε στις 02/02/2009
- ↑ Cajori, Florian (1894), A History of Mathematics, New York, RI: MacMilan and Co., https://en.wikipedia.org/wiki/s:A_History_of_Mathematics/Modern_Europe/Vieta_to_Descartes, σ. 165
- ↑ 24,0 24,1 Maor 2009, ενότητες1, 13
- ↑ Eves, Howard Whitley (1992), An introduction to the history of mathematics, The Saunders series (6th έκδοση), Philadelphia: Saunders, ISBN 978-0-03-029558-4, ενότητα 9-3
- ↑ Boyer, Carl B. (1991), A History of Mathematics, New York: John Wiley & Sons, ISBN 978-0-471-54397-8, https://archive.org/details/historyofmathema00boye, σ. 484, 489
- ↑ Bryant, Walter W., A History of Astronomy, London: Methuen & Co, http://www.forgottenbooks.org/ebooks/A_History_of_Astronomy_-_9781440057922.pdf, ανακτήθηκε στις 2011-10-10, σ. 44
- ↑ Campbell-Kelly, Martin (2003), The history of mathematical tables: from Sumer to spreadsheets, Oxford scholarship online, Oxford University Press, ISBN 978-0-19-850841-0, ενότητα 2
- ↑ Abramowitz, Milton; Stegun, Irene A., επιμ.. (1972), Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (10th έκδοση), New York: Dover Publications, ISBN 978-0-486-61272-0, https://archive.org/details/handbookofmathe000abra, ενότητα 4.7., σ. 89
- ↑ Spiegel, Murray R.; Moyer, R.E. (2006), Schaum's outline of college algebra, Schaum's outline series, New York: McGraw-Hill, ISBN 978-0-07-145227-4, σ. 264
- ↑ Devlin, Keith (2004), Sets, functions, and logic: an introduction to abstract mathematics, Chapman & Hall/CRC mathematics (3rd έκδοση), Boca Raton, Fla: Chapman & Hall/CRC, ISBN 978-1-58488-449-1
- ↑ 32,0 32,1 Lang, Serge (1997), Undergraduate analysis, Undergraduate Texts in Mathematics (2η έκδοση), Berlin, New York: Springer-Verlag, MR 1476913, ISBN 978-0-387-94841-6, ενότητα III.3.
- ↑ 33,0 33,1 Lang 1997, ενότητα IV.2
- ↑ Stewart, James (2007), Single Variable Calculus: Early Transcendentals, Belmont: Thomson Brooks/Cole, ISBN 978-0-495-01169-9, ενότητα 1.6
- ↑ Wolfram Research, Wolfram Alpha, http://www.wolframalpha.com/input/?i=d/dx(Log(b,x)), ανακτήθηκε στις 15/03/2011
- ↑ Kline, Morris (1998), Calculus: an intuitive and physical approach, Dover books on mathematics, New York: Dover Publications, ISBN 978-0-486-40453-0, σ. 386
- ↑ Wolfram Research, Wolfram Alpha, http://www.wolframalpha.com/input/?i=Integrate(ln(x)), ανακτήθηκε στις 15/03/2011
- ↑ Abramowitz & Stegun, σελ. 69
- ↑ Courant, Richard (1988), Differential and integral calculus. Vol. I, Wiley Classics Library, New York: John Wiley & Sons, MR 1009558, ISBN 978-0-471-60842-4, ενότητα III.6.
- ↑ Havil, Julian (2003), Gamma: Exploring Euler's Constant, Princeton University Press, ISBN 978-0-691-09983-5, ενότητες 11.5 και 13.8
- ↑ Muller, Jean-Michel (2006), Elementary functions (2nd έκδοση), Boston, MA: Birkhäuser Boston, ISBN 978-0-8176-4372-0, ενότητες 4.2.2 (σ. 72) και 5.5.2 (σ. 95)
- ↑ Hart, Cheney, Lawson et al. (1968), Computer Approximations, SIAM Series in Applied Mathematics, New York: John Wiley, ενότητα 6.3, σ. 105–111
- ↑ Zhang, M.; Delgado-Frias, J.G.; Vassiliadis, S. (1994), «Table driven Newton scheme for high precision logarithm generation», IEE Proceedings Computers & Digital Techniques 141 (5): 281–292, ISSN 1350-387, ενότητα 1 για επισκόπιση του θέματος
- ↑ Nomizu, Katsumi (1996), Selected papers on number theory and algebraic geometry, 172, Providence, RI: AMS Bookstore, σελ. 21, ISBN 978-0-8218-0445-2, http://books.google.com/books?id=uDDxdu0lrWAC&pg=PA21
- ↑ Baker, Alan (1975), Transcendental number theory, Cambridge University Press, ISBN 978-0-521-20461-3, σ. 10
- ↑ 46,0 46,1 Abramowitz & Stegun 1972, σ. 68
- ↑ Sasaki, T.; Kanada, Y. (1982), «Practically fast multiple-precision evaluation of log(x)», Journal of Information Processing 5 (4): 247–250, http://ci.nii.ac.jp/naid/110002673332, ανακτήθηκε στις 30 March 2011
- ↑ Ahrendt, Timm (1999), Fast computations of the exponential function, Lecture notes in computer science, 1564, Berlin, New York: Springer, σελ. 302–312, doi:
- ↑ Maor 2009, σελ. 135
- ↑ Frey, Bruce (2006), Statistics hacks, Hacks Series, Sebastopol, CA: O'Reilly, ISBN 978-0-596-10164-0, http://books.google.com/?id=HOPyiNb9UqwC&pg=PA275&dq=statistics+hacks+benfords+law#v=onepage&q&f=false, κεφάλαιο 6, ενότητα 64
- ↑ Ricciardi, Luigi M. (1990), Lectures in applied mathematics and informatics, Manchester: Manchester University Press, ISBN 978-0-7190-2671-3, http://books.google.de/books?id=Cw4NAQAAIAAJ, σ. 21, ενότητα 1.3.2
- ↑ Bakshi, U. A. (2009), Telecommunication Engineering, Pune: Technical Publications, ISBN 978-81-8431-725-1, http://books.google.com/books?id=EV4AF0XJO9wC&pg=SA5-PA1#v=onepage&f=false[νεκρός σύνδεσμος], ενότητα 5.2
- ↑ Maling, George C. (2007), «Noise», στο: Rossing, Thomas D., επιμ., Springer handbook of acoustics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-30446-5, ενότητα 23.0.2
- ↑ Tashev, Ivan Jelev (2009), Sound Capture and Processing: Practical Approaches, New York: John Wiley & Sons, ISBN 978-0-470-31983-3, http://books.google.com/books?id=plll9smnbOIC&pg=PA48#v=onepage&f=false, σ. 48
- ↑ Chui, C.K. (1997), Wavelets: a mathematical tool for signal processing, SIAM monographs on mathematical modeling and computation, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-384-8, http://books.google.com/books?id=N06Gu433PawC&pg=PA180#v=onepage&f=false, σ. 180
- ↑ Crauder, Bruce; Evans, Benny; Noell, Alan (2008), Functions and Change: A Modeling Approach to College Algebra (4th έκδοση), Boston: Cengage Learning, ISBN 978-0-547-15669-9, ενότητα 4.4.
- ↑ Bradt, Hale (2004), Astronomy methods: a physical approach to astronomical observations, Cambridge Planetary Science, Cambridge University Press, ISBN 978-0-521-53551-9, ενότητα 8.3, σ. 231
- ↑ IUPAC (1997), A. D. McNaught, A. Wilkinson, επιμ., Compendium of Chemical Terminology ("Gold Book") (2η έκδοση), Oxford: Blackwell Scientific Publications, doi:, ISBN 978-0-9678550-9-7, http://goldbook.iupac.org/P04524.html
- ↑ Bird, J. O. (2001), Newnes engineering mathematics pocket book (3rd έκδοση), Oxford: Newnes, ISBN 978-0-7506-4992-6, ενότητα 34
- ↑ Goldstein, E. Bruce (2009), Encyclopedia of Perception, Encyclopedia of Perception, Thousand Oaks, CA: Sage, ISBN 978-1-4129-4081-8, http://books.google.de/books?id=Y4TOEN4f5ZMC, σ. 355–356
- ↑ Matthews, Gerald (2000), Human performance: cognition, stress, and individual differences, Human Performance: Cognition, Stress, and Individual Differences, Hove: Psychology Press, ISBN 978-0-415-04406-6, http://books.google.de/books?id=0XrpulSM1HUC, σ. 48
- ↑ Welford, A. T. (1968), Fundamentals of skill, London: Methuen, ISBN 978-0-416-03000-6, OCLC 219156, σ. 61
- ↑ Paul M. Fitts (1954), «The information capacity of the human motor system in controlling the amplitude of movement», Journal of Experimental Psychology 47 (6): 381–391, doi:, PMID 13174710, ανατυπωμένο στο Paul M. Fitts (1992), «The information capacity of the human motor system in controlling the amplitude of movement», Journal of Experimental Psychology: General 121 (3): 262–269, doi:, PMID 1402698, http://sing.stanford.edu/cs303-sp10/papers/1954-Fitts.pdf, ανακτήθηκε στις 30 March 2011
- ↑ Banerjee, J. C. (1994), Encyclopaedic dictionary of psychological terms, New Delhi: M.D. Publications, ISBN 9788185880280, OCLC 33860167, http://books.google.com/?id=Pwl5U2q5hfcC&pg=PA306&dq=weber+fechner+law#v=onepage&q=weber%20fechner%20law&f=false, σ. 304
- ↑ Nadel, Lynn (2005), Encyclopedia of cognitive science, New York: John Wiley & Sons, ISBN 978-0-470-01619-0, λήμματα Psychophysics και Perception: Overview
- ↑ Siegler, Robert S.; Opfer, John E. (2003), «The Development of Numerical Estimation. Evidence for Multiple Representations of Numerical Quantity», Psychological Science 14 (3): 237–43, doi:, PMID 12741747, http://www.psy.cmu.edu/~siegler/sieglerbooth-cd04.pdf, ανακτήθηκε στις 2011-10-10
- ↑ Dehaene, Stanislas; Izard, Véronique; Spelke, Elizabeth; Pica, Pierre (2008), «Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures», Science 320 (5880): 1217–1220, doi:, PMID 18511690
- ↑ Breiman, Leo (1992), Probability, Classics in applied mathematics, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-296-4, ενότητα 12.9
- ↑ Aitchison, J.; Brown, J. A. C. (1969), The lognormal distribution, Cambridge University Press, ISBN 978-0-521-04011-2, OCLC 301100935
- ↑ Jean Mathieu and Julian Scott (2000), An introduction to turbulent flow, Cambridge University Press, σελ. 50, ISBN 9780521775380, http://books.google.com/books?id=nVA53NEAx64C&pg=PA50
- ↑ Rose, Colin; Smith, Murray D. (2002), Mathematical statistics with Mathematica, Springer texts in statistics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-95234-5, ενότητα 11.3
- ↑ Tabachnikov, Serge (2005), Geometry and Billiards, Providence, R.I.: American Mathematical Society, σελ. 36–40, ISBN 978-0-8218-3919-5, ενότητα 2.1
- ↑ Durtschi, Cindy; Hillison, William; Pacini, Carl (2004), «The Effective Use of Benford's Law in Detecting Fraud in Accounting Data», Journal of Forensic Accounting V: 17–34, http://lycofs01.lycoming.edu/~sprgene/M400/BenfordsLaw.pdf, ανακτήθηκε στις 2023-09-08
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, ISBN 978-3-540-21045-0, pages 1-2
- ↑ Harel, David; Feldman, Yishai A. (2004), Algorithmics: the spirit of computing, New York: Addison-Wesley, ISBN 978-0-321-11784-7, σ. 143
- ↑ Knuth, Donald (1998), The Art of Computer Programming, Reading, Mass.: Addison-Wesley, ISBN 978-0-201-89685-5, ενότητα 6.2.1, σσ. 409–426
- ↑ Knuth 1998, ενότητα 5.2.4, σσ. 158–168
- ↑ Wegener, Ingo (2005), Complexity theory: exploring the limits of efficient algorithms, Berlin, New York: Springer-Verlag, σελ. 20, ISBN 978-3-540-21045-0
- ↑ Mohr, Hans; Schopfer, Peter (1995), Plant physiology, Berlin, New York: Springer-Verlag, ISBN 978-3-540-58016-4, κεφάλαιο 19, σ. 298
- ↑ Eco, Umberto (1989), The open work, Harvard University Press, ISBN 978-0-674-63976-8, ενότητα III.I
- ↑ Sprott, Julien Clinton (2010), Elegant Chaos: Algebraically Simple Chaotic Flows, New Jersey: World Scientific, ISBN 978-981-283-881-0, http://books.google.com/books?id=buILBDre9S4C, ενότητα 1.9
- ↑ Helmberg, Gilbert (2007), Getting acquainted with fractals, De Gruyter Textbook, Berlin, New York: Walter de Gruyter, ISBN 978-3-11-019092-2
- ↑ Wright, David (2009), Mathematics and music, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4873-9, κεφάλαιο 5
- ↑ Bateman, P. T.; Diamond, Harold G. (2004), Analytic number theory: an introductory course, New Jersey: World Scientific, ISBN 978-981-256-080-3, OCLC 492669517, theorem 4.1
- ↑ Bateman 2004, Theorem 8.15
- ↑ Slomson, Alan B. (1991), An introduction to combinatorics, London: CRC Press, ISBN 978-0-412-35370-3, κεφάλαιο 4
- ↑ Ganguly, S. (2005), Elements of Complex Analysis, Kolkata: Academic Publishers, ISBN 978-81-87504-86-3, Definition 1.6.3
- ↑ Nevanlinna, Rolf Herman; Paatero, Veikko (2007), Introduction to complex analysis, Providence, RI: AMS Bookstore, ISBN 978-0-8218-4399-4, ενότητα 5.9
- ↑ Moore, Theral Orvis; Hadlock, Edwin H. (1991), Complex analysis, Singapore: World Scientific, ISBN 978-981-02-0246-0, ενότητα 1.2
- ↑ Wilde, Ivan Francis (2006), Lecture notes on complex analysis, London: Imperial College Press, ISBN 978-1-86094-642-4, http://books.google.com/?id=vrWES2W6vG0C&pg=PA97&dq=complex+logarithm#v=onepage&q=complex%20logarithm&f=false, theorem 6.1.
- ↑ Higham, Nicholas (2008), Functions of Matrices. Theory and Computation, Philadelphia, PA: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-646-7, κεφάλαιο 11.
- ↑ Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, 1697859, ISBN 978-3-540-65399-8, ενότητα II.5.
- ↑ Hancock, Edwin R.; Martin, Ralph R.; Sabin, Malcolm A. (2009), Mathematics of Surfaces XIII: 13th IMA International Conference York, UK, September 7–9, 2009 Proceedings, Springer, σελ. 379, ISBN 978-3-6-4203595-1, http://books.google.com/books?id=0cqCy9x7V_QC&pg=PA379
- ↑ Stinson, Douglas Robert (2006), Cryptography: Theory and Practice (3rd έκδοση), London: CRC Press, ISBN 978-1-58488-508-5
- ↑ Lidl, Rudolf; Niederreiter, Harald (1997), Finite fields, Cambridge University Press, ISBN 978-0-521-39231-0
- ↑ Corless, R.; Gonnet, G.; Hare, D.; Jeffrey, D.; Knuth, Donald (1996), «On the Lambert W function», Advances in Computational Mathematics (Berlin, New York: Springer-Verlag) 5: 329–359, doi:, ISSN 1019-7168, http://www.apmaths.uwo.ca/~djeffrey/Offprints/W-adv-cm.pdf, ανακτήθηκε στις 2011-10-10
- ↑ Cherkassky, Vladimir; Cherkassky, Vladimir S.; Mulier, Filip (2007), Learning from data: concepts, theory, and methods, Wiley series on adaptive and learning systems for signal processing, communications, and control, New York: John Wiley & Sons, ISBN 978-0-471-68182-3, σ. 357
- ↑ Bourbaki, Nicolas (1998), General topology. Chapters 5—10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, ενότητα V.4.1
- ↑ Ambartzumian, R. V. (1990), Factorization calculus and geometric probability, Cambridge University Press, ISBN 978-0-521-34535-4, ενότητα 1.4
- ↑ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, DMV Seminar, 20, Basel, Boston: Birkhäuser Verlag, ISBN 978-3-7643-2822-1, ενότητα 2
- ↑ Apostol, T.M. (2010), Olver title=NIST Handbook of Mathematical Functions, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. και άλλοι, επιμ., Cambridge University Press, 2723248, ISBN 978-0521192255, http://dlmf.nist.gov/25.12
|














![{\displaystyle \log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca0e5324b82de66458079f9ed2b47bad05a6abbe)














![{\displaystyle {\sqrt[{d}]{c}}=c^{\frac {1}{d}}=b^{{\frac {1}{d}}\log _{b}(c)}.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba9e10fbda0f1ce9dd2d211ec6bc2c80d1f3dd8)














![{\displaystyle {\sqrt {-5+{\sqrt[{3}]{3/13}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75a23d6c4b03445575332e49331570f5bb9aeef3)










![{\displaystyle {\frac {466}{440}}\approx {\frac {493}{466}}\approx 1.059\approx {\sqrt[{12}]{2}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55acf246da64ba711e1717eb43ad81792220ab32)



![{\displaystyle {\begin{aligned}2^{\frac {4}{12}}&={\sqrt[{3}]{2}}\\&\approx 1.2599\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/76610ca7878ea438fa73bd50ac4df1fecce09b9f)


![{\displaystyle \log _{\sqrt[{12}]{2}}(r)=12\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/173477b6bc89e2396abacc83ca5015ac01b0747b)






![{\displaystyle \log _{\sqrt[{1200}]{2}}(r)=1200\log _{2}(r)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1ccc3b05bf5ae0d41f85c50ab1a7ceec4e95713)

















