Τετραδόνιο
Στα μαθηματικά, τα τετραδόνια (quaternions) αποτελούν μία μη-αντιμεταθετική επέκταση της θεωρίας των μιγαδικών αριθμών. Παρουσιάστηκαν για πρώτη φορά από τον Ιρλανδό μαθηματικό Γουίλιαμ Ρόουαν Χάμιλτον το 1843 και εφαρμόστηκαν στη μηχανική μέσα στον τρισδιάστατο χώρο. Η αρχική διατύπωση των εξισώσεων του Maxwell για τον ηλεκτρομαγνητισμό ήταν σε μορφή τετραδονίων. Σήμερα, στις περισσότερες εφαρμογές έχουν αντικατασταθεί από την απλούστερη διανυσματική ανάλυση. Παρόλα αυτά, συναντώνται ακόμη σε εφαρμογές όπως στα τρισδιάστατα γραφικά ηλεκτρονικών υπολογιστών. Η άλγεβρα των τετραδονίων συχνά συμβολίζεται με το γράμμα H (προς τιμήν του Hamilton) ή με το παχύ (Unicode U+210D, ℍ).
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Τα τετραδόνια αποτελούν γενικευμένη μορφή των μιγαδικών αριθμών, που προκύπτουν από την πρόσθεση των βασικών στοιχείων και σε πραγματικούς αριθμούς, όπου τα και ικανοποιούν τη σχέση
και ο πολλαπλασιασμός θεωρείται προσεταιριστικός. Κάθε τετραδόνιο αποτελεί γραμμικό συνδυασμό των βασικών τετραδονίων , και . Έτσι, μπορεί να εκφρασθεί με μοναδικό τρόπο ως:
όπου και είναι πραγματικοί αριθμοί.
Με βάση την προαναφερθείσα σχέση, που ικανοποιούν τα στοιχεία και , προκύπτουν νέες σχέσεις που ικανοποιούν οι ανά δύο συνδυασμοί γινομένων αυτών των στοιχείων. Για παράδειγμα, αν κανείς πολλαπλασιάσει απ' τα δεξιά και τα δύο μέλη της εξίσωσης −1 = ijk με το k, τότε:
Με παρόμοιο τρόπο, μπορούν να εξαχθούν σχέσεις για κάθε δυνατό συνδυασμό, που συνοπτικά είναι οι εξής:
Οι σχέσεις αυτές μπορούν να εκφραστούν και υπό μορφή ενός πίνακα, του οποίου οι γραμμές αναπαριστούν τον αριστερό και οι στήλες το δεξιό παράγοντα του γινομένου, ως εξής:
| a b | a 1 | a i | a j | a k |
| 1 b | 1 | i | j | k |
| i b | i | -1 | k | -j |
| j b | j | -k | -1 | i |
| k b | k | j | -i | -1 |
Μη αντιμεταθετικότητα του πολλαπλασιασμού[Επεξεργασία | επεξεργασία κώδικα]
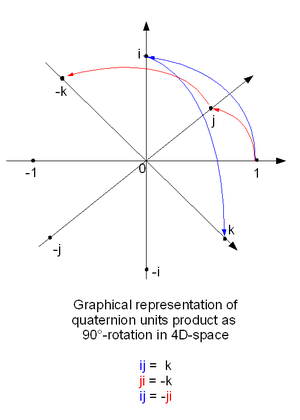
Σε αντίθεση με τον πολλαπλασιασμό των πραγματικών και των μιγαδικών αριθμών, ο πολλαπλασιασμός των τετραδονίων δεν είναι αντιμεταθετικός. Για παράδειγμα, ij = k, ενώ ji = −k. Η μη αντιμεταθετικότητα του πολλαπλασιασμού έχει ορισμένες απροσδόκητες συνέπειες, μεταξύ άλλων το γεγονός ότι οι πολυωνυμικές εξισώσεις σε τετραδόνια, μπορεί να έχουν περισσότερες διακριτές λύσεις από το βαθμό του πολυωνύμου.
Η εξίσωση z2 + 1 = 0, για παράδειγμα, έχει απείρως πολλές λύσεις τετραδονίων της μορφής z = bi + cj + dk, όπου b2 + c2 + d2 = 1, έτσι που οι λύσεις κείτονται σε μια διδιάστατη, σφαιρική επιφάνεια με κέντρο το μηδέν στον τριδιάστατο υπόχωρο των τετραδονίων με μηδενικό πραγματικό μέρος. Αυτή η σφαίρα τέμνει το μιγαδικό επίπεδο σε δύο σημεία, στο i και στο −i.
Το γεγονός, ότι ο πολλαπλασιασμός τετραδονίων δεν είναι αντιμεταθετικός, καθιστά αυτά συχνά αναφερόμενα παραδείγματα ενός αυστηρού πεδίου λοξότητας (skew field).[1]
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]

Ο Γουίλιαμ Ρόουαν Χάμιλτον (William Rowan Hamilton 1805-1865) είχε υπόψη του την γεωμετρική αναπαράσταση των μιγαδικών αριθμών που είχε προτείνει ο Καρλ Φρίντριχ Γκάους (Carl Friedrich Gauss 1777- 1855). Ανέπτυξε τη θεωρία σύμφωνα με την οποία οι μιγαδικοί αριθμοί έχουν τη μορφή επομένως μπορούν να αντιμετωπιστούν ως διατεταγμένα ζεύγη και να συστηματοποιηθούν ως μια άλγεβρα διατεταγμένων ζευγών. Έπειτα από αυτό ο Χάμιλτον ήθελε να γενικεύσει την ιδέα των ζευγών σε τριάδες αλλά δεν μπόρεσε να ορίσει τις πράξεις τους, τη διαίρεση και τον πολλαπλασιασμό, διότι δεν μπορούσε να υπολογίσει το πηλίκο των συντεταγμένων δύο σημείων στο χώρο. Στις 16 Οκτωβρίου 1843[2] στο Δουβλίνο,καθώς περπατούσε με τη γυναίκα του, σχηματοποιήθηκε στο μυαλό του η μορφή των τετράδων (quaternions) με αποτέλεσμα να χαράξει σε μία πέτρα της Μπρούμ (Brougham Broom) γέφυρας τη φόρμουλα των τετράδων:
Την επόμενη μέρα, έστειλε στον μαθηματικό Τζον Τόμας Γκρέιβς (John Thomas Graves 1806–1870) τη σκέψη του για αυτή την ανακάλυψη και αργότερα το γράμμα αυτό δημοσιεύτηκε στο περιοδικό "London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science"[3], το οποίο ανέφερε "Ξαφνικά συνειδητοποίησα την ιδέα την οποία πρέπει να παραδεχτούμε, ότι με κάποια έννοια, μια τέταρτη διάσταση του χώρου με στόχο τον υπολογισμό των τριάδων... Ένα κύκλωμα φάνηκε να κλείνει και μία σπίθα έλαμψε εμπρός."
Στην Ελλάδα αναφορά στα στοιχεία των τετράδων του Hamilton και κάποια ίχνη των ιδεών Grassmann έχουμε στο βιβλίο "Ανωτέρα Άλγεβρα"(1879) του Ιωάννη Χατζιδάκη (1844-1921)[4], καθηγητή στη τότε Σχολή Ευελπίδων. Η πρώτη δημοσιευμένη εργασία για τις τετράδες του Hamilton έγινε το 1883 από τον Κυπάρισσο Στέφανο (1857-1917), καθηγητή Μαθηματικών στο Εθνικό Μετσόβιο Πολυτεχνείο, για το Γερμανικό περιοδικό "Mathematische Annalen" τομέας του Διανυσματικού Λογισμού ο οποίος δεν αναπτύχθηκε διδακτικά και ερευνητικά στην Ελλάδα.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
Άρθρα και πηγές[Επεξεργασία | επεξεργασία κώδικα]
- Geometric Tools documentation Includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
- Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
- Geometric Tools source code Includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
- Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
- Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.
Εγκυκλοπαίδειες[Επεξεργασία | επεξεργασία κώδικα]
- "Quaternion". 1911 encyclopedia.
- Tait, Peter Guthrie, "Quaternion στη Wayback Machine του Internet Archive (αρχειοθετήθηκε Αύγουστος 8, 2014)". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160–164. (bzipped PostScript file)
Βιβλία και εκδόσεις[Επεξεργασία | επεξεργασία κώδικα]
- Tait, Peter Guthrie, "An elementary treatise on quaternions". 2d ed., Cambridge, [Eng.] : The University Press, c. 1873.
- Macfarlane, Alexander, "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.] 1906. LCCN es 16000048
- Joly, Charles Jasper, "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company, 1905. LCCN 05036137 //r84
- Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser, "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3 1962 207–220, MathSciNet.
- Du Val, Patrick, "Homographies, quaternions, and rotations". Oxford, Clarendon Press, 1964 (Oxford mathematical monographs). LCCN 64056979 //r81
- Crowe, Michael J. (1967). A History of Vector Analysis: The Evolution of the Idea of a Vectorial System University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, MacFarlane, MacAuley, Gibbs, Heaviside). The competition between quaternions and other systems is a major theme.
- Adler, Stephen L., "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press, 1995. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X (alk. paper)
- Altmann, Simon L., "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press, c1986. LCCN 85013615 ISBN 0-19-855372-2
- Ward, J. P. (1997). Quaternions and Cayley Numbers: Algebra and Applications, Kluwer Academic Publishers. ISBN 0-7923-4513-4.
- Gürlebeck, Klaus and Wolfgang Sprössig, "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley, c1997 (Mathematical methods in practice; v. 1) LCCN 98169958 ISBN 0-471-96200-7 (acid-free paper)
- Kuipers, Jack (2002). Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality (Reprint edition). Princeton University Press. ISBN 0-691-10298-8
- Conway, John Horton, and Smith, Derek A., (2003) On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd.
- [2] Hanson, Andrew J., "Visualizing Quaternions". Elsevier : Morgan Kaufmann ; San Fransisco : (2006). ISBN 0-12-088400-3
Λογισμικό[Επεξεργασία | επεξεργασία κώδικα]
- Euler Quaternion Pro A free GUI based utility that converts Euler angles to Quaternions around X,Y and Z (roll, pitch and yaw) axis and performs conjugate, addition, subtraction, multiplication, great circle interpolation operations on converted Quaternions.
- Quaternion Calculator [Java]
- Quaternion Toolbox for Matlab
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
| |||||||||||||||||||||||||||||
|

























