Διανυσματικός χώρος

Ο διανυσματικός χώρος είναι μια μαθηματική δομή η οποία αποτελείται από μια συλλογή στοιχείων που ονομάζονται διανύσματα[1][2]. Τα διανύσματα μπορούν να προστίθενται και να πολλαπλασιάζονται (κλιμακωτά) με αριθμούς, οι οποίοι στο κείμενο θα ονομάζονται ως βαθμωτά. Τα βαθμωτά είναι συνήθως πραγματικοί αριθμοί, αλλά υπάρχουν και διανυσματικοί χώροι με βαθμωτό πολλαπλασιασμό μιγαδικών αριθμών, ρητών αριθμών ή γενικά οποιουδήποτε σώματος. Οι πράξεις της πρόσθεσης και του βαθμωτού πολλαπλασιασμού πρέπει να πληρούν κάποιες προϋποθέσεις, οι οποίες καλούνται αξιώματα, παρατίθενται παρακάτω. Ένα παράδειγμα διανυσματικού χώρου είναι αυτός των ευκλείδειων διανυσμάτων, τα οποία μπορούν να χρησιμοποιηθούν για να αναπαραστήσουν φυσικές ποσότητες όπως είναι οι δυνάμεις• οποιαδήποτε δυο διανύσματα δυνάμεων (ίδιου τύπου) μπορούν να προστεθούν για να παράγουν ένα τρίτο και ο πολλαπλασιασμός ενός διανύσματος δύναμης με έναν πραγματικό πολλαπλασιαστή, είναι ένα νέο διάνυσμα δύναμης. Από γεωμετρικής άποψης, τα διανύσματα που εκπροσωπούν μετατοπίσεις στο επίπεδο ή στον τρισδιάστατο χώρο αποτελούν επίσης διανυσματικούς χώρους.
Οι διανυσματικοί χώροι είναι αντικείμενο μελέτης της γραμμικής άλγεβρας μιας και χαρακτηρίζονται από τη διάστασή τους, η οποία καθορίζει τον αριθμό των ανεξάρτητων κατευθύνσεων στο χώρο. Ο διανυσματικός χώρος μπορεί να να εμπλουτιστεί με πρόσθετη δομή όπως είναι το μέτρο διανύσματος και το εσωτερικό γινόμενο.
Ιστορικά, οι πρώτες ιδέες που οδήγησαν στους διανυσματικούς χώρους μπορούν να εντοπιστούν πίσω στον χρόνο όσον αφορά την αναλυτική γεωμετρία του 17ου αιώνα, τους πίνακες, τα συστήματα εξισώσεων ευθείας, και τα Ευκλείδεια διανύσματα. Η σύγχρονη, πιο αφηρημένη αναφορά έγινε από τον Τζουζέπε Πεάνο το 1888. Σήμερα οι διανυσματικοί χώροι βρίσκουν εφαρμογή στο σύνολο των μαθηματικών, της επιστήμης και στις επιστήμες μηχανικών.
Εισαγωγή και ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Παράδειγμα πρώτο: Βέλη στο επίπεδο[Επεξεργασία | επεξεργασία κώδικα]
Το πρώτο παράδειγμα ενός διανυσματικού χώρου αποτελείται από τα βέλη σε ένα σταθερό επίπεδο, ξεκινώντας από ένα σταθερό σημείο. Αυτό χρησιμοποιείται στη φυσική για να περιγράψει τις δυνάμεις και τις ταχύτητες. Έχοντας δυο τέτοια βέλη, και , η διαγώνιος του παραλληλογράμμου που σχηματίζουν, είναι επίσης ένα βέλος που ξεκινάει από το ίδιο σημείο ορισμού[2]. Αυτό το διαγώνιο βέλος το ονομάζουμε άθροισμα και το συμβολίζουμε με . Στην ειδική περίπτωση που τα δύο βέλη έχουν την ίδια γραμμή διεύθυνσης, το άθροισμα τους είναι εκείνο το βέλος που έχει μέγεθος (ή μέτρο) ίσο με το αλγεβρικό άθροισμα των μέτρων των δύο αρχικών βελών, δηλαδή τα μέτρα προστίθενται όταν τα διανύσματα έχουν την ίδια κατεύθυνση και αφαιρούνται όταν έχουν την αντίθετη. Μια άλλη διεργασία που μπορεί να επιτευχθεί με τα βέλη είναι η αλλαγή κλίμακας στην οποία ένας οποιουδήποτε θετικός πραγματικός αριθμός μέσο του πολλαπλασιασμού του με ένα βέλος έχει σαν αποτέλεσμα ένα άλλο βέλος που έχει την ίδια φορά με το αλλά επεκτείνεται () ή συρρικνώνεται () σύμφωνα με το μήκος του . Η πράξη αυτή ονομάζεται πολλαπλασιασμός του με το βαθμωτό μέγεθος και συμβολίζεται με . Αν ο αριθμός είναι αρνητικός, τότε το ορίζεται ως βέλος που δείχνει προς την αντίθετη κατεύθυνση. Οι παρακάτω εικόνες δείχνουν δυο παραδείγματα: αν , το διάνυσμα που προκύπτει έχει την ίδια κατεύθυνση με το , αλλά είναι επεκτεταμένο κατά το διπλάσιο μήκος του (δεξιά εικόνα). Ισοδύναμα είναι το άθροισμα . Από την άλλη, , έχει την αντίθετη κατεύθυνση αλλά το ίδιο μήκος με το .[3]
Παράδειγμα δεύτερο: Διατεταγμένα ζεύγη αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Ένα δεύτερο παράδειγμα ενός διανυσματικού χώρου παρέχεται από ζεύγη πραγματικών αριθμών και . (Η σειρά των συνιστωσών και είναι καθοριστική, γι' αυτό το λόγο ένα τέτοιο ζεύγος ονομάζεται διατεταγμένο). Το ζεύγος αυτό γράφεται ως . Η πρόσθεση δυο ζευγών και ο πολλαπλασιασμός ενός με έναν αριθμό απεικονίζεται παρακάτω:
και
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Ένας διανυσματικός χώρος πάνω από ένα σώμα είναι ένα σύνολο εφοδιασμένο με δυο πράξεις, οι οποίες ικανοποιούν τα οχτώ αξιώματα που παρατίθενται παρακάτω. Τα στοιχεία του συνόλου ονομάζονται διανύσματα. Τα στοιχεία του συνόλου ονομάζονται βαθμωτά. Στα δύο παραπάνω παραδείγματα, το σύνολο μας αποτελείται από τα επίπεδα βέλη με σταθερό σημείο εκκίνησης και τα ζεύγη των πραγματικών αριθμών, αντίστοιχα, ενώ το σώμα μας είναι οι πραγματικοί αριθμοί.[4][2]
Για να χαρακτηρισθεί ένας χώρος ως διανυσματικός , το σύνολο και οι πράξεις της πρόσθεσης και του πολλαπλασιασμού πρέπει να τηρούν ορισμένες προϋποθέσεις που ονομάζονται αξιώματα. Στην παρακάτω λίστα, έστω , και είναι αυθαίρετα διανύσματα στο , και και βαθμωτά στο .
| Αξιώματα | Σημασία |
| Προσεταιριστική ιδιότητα της πρόσθεσης | |
| Αντιμεταθετική ιδιότητα της πρόσθεσης | |
| Ουδέτερο στοιχείο της πρόσθεσης | Υπάρχει ένα στοιχείο , που ονομάζεται μηδενικό διάνυσμα, τέτοιο ώστε για κάθε . |
| Αντίθετο στοιχείο της πρόσθεσης | Για κάθε , υπάρχει ένα στοιχείο , που ονομάζεται προσθετικό αντιστροφής του , τέτοιο ώστε . |
| Συμβατότητα του βαθμωτού πολλαπλασιασμού με τον πολλαπλασιασμό στοιχείων των σωμάτων | . |
| Ουδέτερο στοιχείο του βαθμωτού πολλαπλασιασμού | , όπου το υποδηλώνει την πολλαπλασιαστική ταυτότητα στον . |
| Επιμεριστική ιδιότητα σε σχέση με την προσθήκη διανύσματος | . |
| Επιμεριστική ιδιότητα σε σχέση με την προσθήκη στοιχείων του σώματος | . |
Αυτά τα αξιώματα γενικεύουν τις ιδιότητες των διανυσμάτων που εφαρμόστηκαν στα ανωτέρω παραδείγματα. Πράγματι, το αποτέλεσμα της πρόσθεσης των δύο διατεταγμένων ζευγών (όπως στο δεύτερο παράδειγμα) δεν εξαρτάται από τη σειρά των αθροισμάτων:
Ομοίως, στο γεωμετρικό παράδειγμα των διανυσμάτων ως βέλη, , δεδομένου ότι το παραλληλόγραμμο που καθορίζει το άθροισμα των διανυσμάτων είναι ανεξάρτητο της σειράς των διανυσμάτων. Όλα τα άλλα αξιώματα μπορούν να ελεγχθούν με παρόμοιο τρόπο και στα δύο παραδείγματα.
Η αφαίρεση μεταξύ δυο διανυσμάτων και η διαίρεση με (μη μηδενικό) βαθμωτό μπορούν να οριστούν ως εξής:
Όταν το βαθμωτό σώμα είναι οι πραγματικοί αριθμοί , ο διανυσματικός χώρος ονομάζεται πραγματικός διανυσματικός χώρος. Όταν το βαθμωτό σώμα είναι των μιγαδικών αριθμών, αυτό ονομάζεται μιγαδικός διανυσματικός χώρος. Αυτές οι δύο περιπτώσεις είναι εκείνες που χρησιμοποιούνται πιο συχνά στη μηχανική. Ο πιο γενικός ορισμός ενός διανυσματικού χώρου, επιτρέπει βαθμωτά να είναι τα στοιχεία του οποιουδήποτε σταθερού σώματος . Η έννοια είναι γνωστή τότε ως ένα Κ-διανυσματικός χώρος ή διανυσματικός χώρος επί του . Ένα σώμα είναι, ουσιαστικά, ένα σύνολο αριθμών που διαθέτει τις πράξεις της πρόσθεσης, της αφαίρεσης, του πολλαπλασιασμού και της διαίρεσης. Για παράδειγμα, οι ρητοί αριθμοί αποτελούν επίσης ένα σώμα.
Γενικά στους διανυσματικούς χώρους δεν υπάρχουν οι έννοιες της εγγύτητας, της γωνίας ή της απόστασης. Για να αντιμετωπίσουμε αυτό το πρόβλημα εισάγουμε παρακάτω συγκεκριμένους τύπους διανυσματικών χώρων.
Το ότι ότι η πρόσθεση και βαθμωτός πολλαπλασιασμός διανυσμάτων είναι δυαδικές πράξεις, οδηγεί στη δημιουργία μια νέας ιδιότητα που χαρακτηρίζει τις δυο αυτές πράξεις κλειστές, δηλαδή ότι και αv ανήκουν στο για κάθε , και .
Στην αφηρημένη άλγεβρα, τα πρώτα τέσσερα αξιώματα μπορούν να υπαχθούν απαιτώντας το σύνολο των διανυσμάτων να είναι μια αβελιανή ομάδα κάτω από ένα μόνο αξίωμα. Τα υπόλοιπα αξιώματα δίνουν μια συγκεκριμένη ομάδα την δομή Κ-module. Με άλλα λόγια, υπάρχει ένας δακτύλιος ομομορφισμού από το πεδίο στο δακτύλιο ενδομορφισμού της ομάδας των διανυσμάτων. Τότε ο βαθμωτός πολλαπλασιασμός ορίζεται ως .
Υπάρχει μια σειρά από συνέπειες των αξιωμάτων των διανυσματικών χώρων. Κάποιες από αυτές προέρχονται από την στοιχειώδη θεωρία της ομάδας, που εφαρμόζεται στο σύνολο των διανυσμάτων. Για παράδειγμα, το μηδενικό διάνυσμα του και το πρόσθετο αντίστροφης για κάθε διάνυσμα είναι μοναδικά. Άλλες ιδιότητες απορρέουν από την επιμεριστική, για παράδειγμα, αν και μόνο αν ή .
Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]
Χώροι συντεταγμένων[Επεξεργασία | επεξεργασία κώδικα]
Το πιο απλό παράδειγμα διανυσματικών χώρων πάνω από ένα σώμα είναι το ίδιο το σώμα, εφοδιασμένο με τις συνήθεις πράξεις της πρόσθεση και του πολλαπλασιασμού. Γενικότερα, ένας διανυσματικός χώρος μπορεί να αποτελείται από n-πλειάδες (ακολουθίες μήκους ) των στοιχείων του , όπως:
Ένας διανυσματικός χώρος που αποτελείται από το σύνολο των n-πλειάδων ενός πεδίου είναι γνωστός ως ένας χώρος συντεταγμένων, που συνήθως συμβολίζονται με . Η περίπτωση είναι το προαναφερθέν απλούστερο παράδειγμα, στο οποίο το σώμα θεωρείται επίσης ως ένας διανυσματικός χώρος πάνω από τον εαυτό του. Η περίπτωση και συζητήθηκε στο παράδειγμα 2 παραπάνω.
Οι μιγαδικοί αριθμοί και επεκτεταμένα σώματα[Επεξεργασία | επεξεργασία κώδικα]
Το σύνολο των μιγαδικών αριθμών , δηλαδή, οι αριθμοί που μπορούν να γραφτούν στη μορφή για τους πραγματικούς αριθμούς και , όπου να είναι η φανταστική μονάδα, σχηματίζουν ένα διανυσματικό χώρο πάνω από τους πραγματικούς αριθμούς με τη συνήθη πρόσθεση και πολλαπλασιασμό: και για πραγματικούς αριθμούς . Τα αξιώματα των διανυσματικών χώρων ισχύουν και για τους μιγαδικούς μιας και ισχύουν οι ίδιοι κανόνες για τις αριθμητικές πράξεις και στους μιγαδικούς.
Στην πραγματικότητα, το παράδειγμα των μιγαδικών αριθμών είναι ουσιαστικά το ίδιο (δηλαδή, είναι ισομορφισμός) προς το διανυσματικό χώρο των διατεταγμένων ζευγών στους πραγματικούς αριθμούς που αναφέρονται παραπάνω. Αν θεωρήσουμε τον μιγαδικό αριθμό ότι αντιστοιχεί στο διατεταγμένο ζεύγος στο μιγαδικό επίπεδο, τότε βλέπουμε ότι οι κανόνες για άθροισμα και βαθμωτό πολλαπλασιασμό αντιστοιχούν ακριβώς σε εκείνους του προηγούμενου παραδείγματος.
Γενικότερα, οι επεκτάσεις σωμάτων παρέχουν μια άλλη κατηγορία παραδειγμάτων των διανυσματικών χώρων: ένα σώμα που περιέχει ένα μικρότερο σώμα \mathcal{E}, είναι ένας Ε-διανυσματικός χώρος, με τον δεδομένο πολλαπλασιασμό και τις λειτουργίες της πρόσθεση του . Για παράδειγμα οι μιγαδικοί αριθμοί είναι ένας διανυσματικός χώρος πάνω από το και το επεκτεταμένο σώμα είναι διανυσματικός χώρος πάνω από το .
Συναρτησιακοί χώροι[Επεξεργασία | επεξεργασία κώδικα]
Συναρτήσεις από οποιοδήποτε σταθερό σύνολο σε ένα σώμα , αποτελούν επίσης διανυσματικούς χώρους, εκτελώντας την πρόσθεση και τον βαθμωτό πολλαπλασιασμό σημειακά. Δηλαδή, το άθροισμα των δύο συναρτήσεις και είναι η συνάρτηση και δίνεται από τον τύπο
όμοια πραγματοποιείται και ο πολλαπλασιασμός. Οι αλγεβρικοί περιορισμοί μπορούν να δώσουν επίσης διανυσματικούς χώρους, για παράδειγμα ο διανυσματικός χώρος Κ[x] δίνεται από την πολυωνυμική συνάρτηση:
Γραμμικές εξισώσεις[Επεξεργασία | επεξεργασία κώδικα]
Συστήματα ομογενών γραμμικών εξισώσεων είναι στενά συνδεδεμένα με διανυσματικούς χώρους, για παράδειγμα η λύση του συστήματος
δίνεται από τριάδες αυθαίρετων μεταβλητών . Επειδή τα αθροίσματα και τα βαθμωτά πολλαπλάσια των μεταβλητών ικανοποιούν τις ίδιες αναλογίες με τις αρχικές μεταβλητές, συνεπάγεται ότι και αυτά αποτελούν λύσεις του συστήματος, έτσι δημιουργείται ένας διανυσματικός χώρος. Οι πίνακες μπορούν να χρησιμοποιηθούν για να συμπυκνώσουμε πολλές γραμμικές εξισώσεις σε μία διανυσματική, δηλαδή
- ,
όπου είναι ο πίνακας που περιέχει τους συντελεστές των δοθέντων εξισώσεων, είναι το διάνυσμα , ως δηλώνεται το γινόμενο των πινάκων και το μηδενικό διάνυσμα. Σε παρόμοιο ύφος, οι λύσεις ομογενών γραμμικών διαφορικών εξισώσεων αποτελούν διανυσματικό χώρο. Για παράδειγμα
δίνει , όπου είναι αυθαίρετες σταθερές, και είναι η φυσική εκθετική συνάρτηση.
Βάση και διάσταση[Επεξεργασία | επεξεργασία κώδικα]

[5]Οι βάσεις επιτρέπουν την εισαγωγή συντεταγμένων ως μέσο αναπαράστασης διανυσμάτων. Μια βάση είναι μια (πεπερασμένη ή μη πεπερασμένη) ομάδα διανυσμάτων , για ευκολία συχνά έχει ως δείκτες ένα σύνολο δεικτών [6], που συνδέει όλο το χώρο και είναι γραμμικά ανεξάρτητη. «Σύνδεση όλου του χώρου» σημαίνει ότι κάθε διάνυσμα v μπορεί να εκφραστεί ως ένα πεπερασμένο άθροισμα (ονομάζεται γραμμικός συνδυασμός) των στοιχείων της βάσης:
Όπου τα είναι βαθμωτά, ονομάζονται συντεταγμένες του διανύσματος ως προς τη βάση και με τα στοιχεία του . Γραμμική ανεξαρτησία σημαίνει ότι οι συντεταγμένες είναι μοναδικές για κάθε διάνυσμα στο διανυσματικό χώρο.
Για παράδειγμα, τα διατεταγμένα διανύσματα , από μία βάση του , ονομάζεται κανονική βάση, αφού κάθε διάνυσμα μπορεί να εκφραστεί μοναδικά ως γραμμικός συνδυασμός
Οι αντίστοιχες συντεταγμένες είναι ακριβώς οι καρτεσιανές συντεταγμένες του διανύσματος.
Κάθε διανυσματικός χώρος έχει μία βάση. Αυτό συνάγεται από το λήμμα του Zorn, έναν ισοδύναμο τύπο από το αξίωμα της επιλογής. Δεδομένων των άλλων αξιωμάτων της θεωρίας των συνόλων των Zermelo-Fraenkel, η ύπαρξη βάσεων είναι ισοδύναμη με το αξίωμα της επιλογής. Το λήμμα του υπερφίλτρου, το οποίο είναι πιο αδύναμο από το αξίωμα της επιλογής, υπονοεί ότι όλες οι βάσεις ενός δοσμένου διανυσματικού χώρου έχουν τον ίδιο αριθμό στοιχείων, ή πληθάριθμο θεώρημα διάστασης για διανυσματικούς χώρους. Ονομάζεται διάσταση του διανυσματικού χώρου, συμβολίζεται με dimV. Αν ο χώρος συνδέεται από πολλά πεπερασμένα διανύσματα οι παρακάτω προτάσεις μπορούν να αποδειχθούν χωρίς τόσο θεμελιώδη συμβολή από τη θεωρία συνόλων.
Η διάσταση από το διατεταγμένο χώρο είναι , από τη βάση που παρουσιάζεται πιο πάνω. Η διάσταση του πολυωνυμικού δακτυλίου που παρουσιάστηκε πιο πάνω είναι αριθμητικά άπειρη, η βάση έχει δοθεί . Κατά μείζονα λόγο, η διάσταση πιο γενικών συναρτησιακών χώρων, όπως ο χώρος των συναρτήσεων σε κάποια (φραγμένα ή μη φραγμένα) μεσοδιαστήματα, είναι άπειρη. Κάτω από βολική ομαλότητα, υποθέσεις σε συντελεστές που συμπεριλαμβάνονται, η διάσταση του χώρου των λύσεων μιας ομογενούς συνήθους διαφορικής εξίσωσης ισούται με το βαθμό της εξίσωσης. Για παράδειγμα, ο χώρος των λύσεων για την παραπάνω εξίσωση παράγεται από και το . Αυτές οι δύο συναρτήσεις είναι γραμμικά ανεξάρτητες στο , οπότε η διάσταση του χώρου είναι δύο, όπως και ο βαθμός της εξίσωσης.
Η προέκταση ενός πεδίου πάνω στο σύνολο των ρητών αριθμών μπορεί να θεωρηθεί ως ένας διανυσματικός χώρος πάνω στο (ορίζοντας την προσθήκη διανύσματος σαν προσθήκη πεδίου, τον βαθμωτό πολλαπλασιασμό ως πολλαπλασιασμό πεδίου με στοιχεία του και κατά τ' άλλα αγνοώντας το πεδίο πολλαπλασιασμού). Η διάσταση (ή βαθμός) της επέκτασης πεδίου πέρα από τον εξαρτάται από το . Αν το προϋποθέτει κάποια πολυωνυμική εξίσωση
με ρητούς συντελεστές (ή με άλλα λόγια αν το είναι αλγεβρικό), η διάσταση είναι πεπερασμένη. Ειδικότερα, αυτή ισούται με το βαθμό του ελάχιστου πολυωνύμου έχοντας το ως ρίζα. Για παράδειγμα, οι μιγαδικοί αριθμοί είναι ένας πραγματικός δισδιάστατος διανυσματικός χώρος, που παράγεται από το και τη φανταστική μονάδα . Η τελευταία ικανοποιεί την , μια εξίσωση με βαθμό δύο. Έτσι, ο είναι ένας δισδιάστατος -διανυσματικός χώρος (και, όπως κάθε πεδίο, μονοδιάστατος όπως ένας διανυσματικός χώρος στον εαυτό του, ). Αν το α δεν είναι αλγεβρικό, η διάσταση του στον είναι άπειρη. Για παράδειγμα, για δεν υπάρχει τέτοια εξίσωση, δηλαδή το π είναι υπερβατικό.
Γραμμικές απεικονίσεις και πίνακες[Επεξεργασία | επεξεργασία κώδικα]
Η σχέση των δύο διανυσματικών χώρων μπορεί να εκφραστεί από τη γραμμική απεικόνιση ή γραμμικό μετασχηματισμό. Αυτές είναι συναρτήσεις που αντανακλούν την κατασκευή του διανυσματικού χώρου, δηλαδή διατηρούν την πρόσθεση και τον βαθμωτό πολλαπλασιασμό:[7]
Ένας ισομορφισμός είναι μία γραμμική απεικόνιση έτσι ώστε να υπάρχει μία αντίστροφη απεικόνιση , η οποία είναι μια απεικόνιση όπου οι δύο πιθανές συνθέσεις και να είναι ταυτοτικές απεικονίσεις. Ισοδύναμα, η είναι 1-1 (ένεση) και επί (έφεση). Αν υπάρχει ένας ισομορφισμός ανάμεσα στο και στο , οι δύο χώροι λέγονται ισομορφικοί· αυτοί είναι τότε ουσιαστικά ταυτοτικοί ως διανυσματικοί χώροι, εφόσον όλες οι ταυτότητες που ανήκουν στο μέσω της , μεταφέρονται σε παρόμοιες στον και αντίστροφα μέσω της .

Για παράδειγμα, τα «βέλη στο επίπεδο» και τα «διατεταγμένα ζεύγη αριθμών» στους διανυσματικούς χώρους είναι ισομορφικά: ένα σχεδιασμένο βέλος που παρεκκλίνει στην προέλευση κάποιου (αναθεωρημένου) συστήματος αναφοράς μπορεί να εκφραστεί σαν ένα διατεταγμένο ζεύγος λαμβάνοντας υπόψη το και -στοιχείο του βέλους, όπως φαίνεται στην εικόνα στα δεξιά. Αντίστροφα, έχοντας ένα ζεύγος , το βέλος πηγαίνοντας απ’ το στα δεξιά (ή στα αριστερά, αν το είναι αρνητικό), και απ’ το πάνω (ή κάτω, αν το είναι αρνητικό) γυρίζει πίσω το βέλος .
Οι γραμμικές απεικονίσεις ανάμεσα σε δύο αμετάβλητους διανυσματικούς χώρους σχηματίζουν τον διανυσματικό χώρο , αναγράφεται και . Ο χώρος των γραμμικών απεικονίσεων απ’ τον στον ονομάζεται δυϊκός διανυσματικός χώρος, αναγράφεται και . Μέσω της φυσικής απεικόνισης (και ένεσης) , κάθε διανυσματικός χώρος μπορεί να επεκταθεί στο διπλό του η απεικόνιση είναι ένας ισομορφισμός αν και μόνο αν ο χώρος είναι πεπερασμένης διάστασης.
Όταν μια βάση του είναι επιλεγμένη, οι γραμμικές απεικονίσεις είναι εντελώς καθοριστικές προδιαγράφοντας τις εικόνες των διανυσμάτων της βάσης, γιατί κάθε στοιχείο του εκφράζεται μοναδικά ως ένας γραμμικός συνδυασμός του. Αν , μια 1-1 αντιστοιχία ανάμεσα σε σταθερές βάσεις των και δίνει αύξηση σε μια γραμμική απεικόνιση που απεικονίζει κάθε στοιχείο βάσης του στο αντίστοιχο στοιχείο βάσης του . Είναι ένας ισομορφισμός από τον ίδιο του τον ορισμό. Συνεπώς, δύο διανυσματικοί χώροι είναι ισομορφικοί αν οι διαστάσεις τους συμφωνούν, και αντίστροφα. Με άλλα λόγια, κάθε διανυσματικός χώρος είναι εντελώς "ταξινομημένος" (μέχρι και ισομορφισμό) από τη διάστασή του, ένα μόνο αριθμό. Ειδικότερα, κάθε n-διάστατος F-διανυσματικός χώρος είναι ισομορφικός στον . Υπάρχει, ωστόσο, όχι "κανονικός" ή προτιμότερα ισομορφισμός στην πραγματικότητα ένας ισομορφισμός είναι ισοδύναμος με την επιλογή μιας βάσης του , μέσω της . Η ελευθερία επιλογής μια βολικής βάσης είναι ιδιαίτερα χρήσιμη στο απειρο-διάστατο γενικό πλαίσιο παρακάτω.
Πίνακες[Επεξεργασία | επεξεργασία κώδικα]
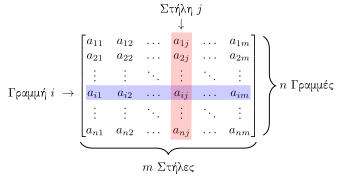
Οι πίνακες είναι μια χρήσιμη ιδέα για να απεικονίσουμε γραμμικές απεικονίσεις. Γράφονται σαν έναν ορθογώνιο πίνακα με βαθμούς(scalars), όπως στην εικόνα στα δεξιά. Κάθε πίνακας είναι (ή περιγράφει) μια γραμμική απεικόνιση από τον στον σύμφωνα με το παρακάτω
όπου συμβολίζει άθροιση,
ή χρησιμοποιώντας τον πολλαπλασιασμό πινάκων του πίνακα με το διατεταγμένο διάνυσμα
Επιπλέον, μετά την επιλογή βάσεων των και , κάθε γραμμική απεικόνιση φαίνεται μοναδικά από έναν πίνακα μέσω αυτής της τοποθέτησης.
Η ορίζουσα ενός τετραγωνικού πίνακα είναι μια τιμή (βαθμωτή) που δείχνει αν η σχετική απεικόνιση είναι ισομορφισμός ή όχι: αν είναι έτσι είναι ικανό και αναγκαίο η ορίζουσα να είναι διάφορη του μηδενός. Ο γραμμικός μετασχηματισμός του που αντιστοιχεί σε έναν πραγματικό πίνακα διατηρεί τον προσανατολισμό του αν και μόνον αν η ορίζουσά του είναι θετική.
Διανυσματικοί χώροι με πρόσθετη δομή[Επεξεργασία | επεξεργασία κώδικα]
Κανονικοί διανυσματικοί χώροι και εσωτερικά γινόμενα[Επεξεργασία | επεξεργασία κώδικα]
Ο "υπολογισμός" διανυσμάτων γίνεται προσδιορίζοντας το μέτρο τους, ένα δεδομένο το οποίο υπολογίζει μήκη διανυσμάτων, ή από ένα εσωτερικό γινόμενο, το οποίο μετράει γωνίες ανάμεσα στα διανύσματα. Τα μέτρα και τα εσωτερικά γινόμενα συμβολίζονται με και αντίστοιχα. Το δεδομένο ενός εσωτερικού γινομένου συνεπάγεται ότι τα μήκη των διανυσμάτων μπορούν να οριστούν επίσης, ορίζοντας το αντίστοιχο μέτρο . Οι διανυσματικοί χώροι ενσωματώνουν τόσες πολλές πληροφορίες ώστε να είναι γνωστοί ως διανυσματικοί χώροι μέτρων και εσωτερικών γινομένων, αντίστοιχα. Ο διατεταγμένος χώρος μπορεί να εφοδιαστεί με το σύνηθες εσωτερικό γινόμενο[2]:
Στον , αυτό αντανακλά τη συνήθη ιδέα της γωνίας ανάμεσα στα δύο διανύσματα και , από το νόμο των συνημίτονων:
Εξαιτίας αυτού, δύο διανύσματα που ικανοποιούν τη ονομάζονται ορθογώνια ή κάθετα μεταξύ τους. Μια σημαντική παραλλαγή του συνήθους γινομένου χρησιμοποιείται στο χώρο Μινκόβσκι: όπου προσδίδεται το γινόμενο Lorentz
Σε αντίθεση με το σύνηθες εσωτερικό γινόμενο, αυτό δεν είναι θετικά ορισμένο. Επιπλέον το παίρνει αρνητικές τιμές, για παράδειγμα όταν το . Απομονώνοντας την τέταρτη συντεταγμένη - που αντιστοιχεί στον χρόνο, σε αντίθεση με την τρισδιάστατη περιγραφή του χώρου - το καθιστά χρήσιμο για τη μαθηματική αντιμετώπιση της ειδικής σχετικότητας.[8]
Περαιτέρω ανάγνωση[Επεξεργασία | επεξεργασία κώδικα]
Ελληνικά άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- «Για τη Β' Τάξη: Διανυσματικοί Χώροι». Ευκλείδης Β΄ (3): 116-121. 1978. http://www.hms.gr/apothema/?s=sa&i=3929.
- Θ. Εξαρχάκος (1979). «Για τη Β' Τάξη: Διανυσματικοί ή Γραμμικοί Χώροι». Ευκλείδης Β΄ (3): 162-171. http://www.hms.gr/apothema/?s=sa&i=4127.
- Β. Γεωργίου; Β. Ζώτος; Σ. Λουρίδας (1980). «Διανυσματικοί Χώροι». Ευκλείδης Β΄ (4): 39-42. http://www.hms.gr/apothema/?s=sa&i=4140.
- Π. Γριμανέλλης; Π. Ελευθερίου (1984). «Διανυσματικοί Χώροι-Υπόχωροι». Ευκλείδης Β΄ (3): 51-59. http://www.hms.gr/apothema/?s=sa&i=3168.
Ξενόγλωσσα άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- Ficken, F. A. (Οκτωβρίου 1940). «Cones and Vector Spaces». The American Mathematical Monthly 47 (8): 530–533. doi:.
- Carchidi, Michael A. (Σεπτεμβρίου 1998). «Generating Exotic-Looking Vector Spaces». The College Mathematics Journal 29 (4): 304. doi:. https://archive.org/details/sim_college-mathematics-journal_1998-09_29_4/page/304.
- Liebeck, Hans (Φεβρουαρίου 1972). «The Vector Space Axiom 1v = v». The Mathematical Gazette 56 (395): 30–33. doi:.
- Bolt, Brian (Ιουλίου 1992). «From magic triangles to vector spaces to magic tetrahedrons». The Mathematical Gazette 76 (476): 257–260. doi:. https://archive.org/details/sim_mathematical-gazette_1992-07_76_476/page/257.
- Crilly, Tony (Ιουνίου 1976). «A circular vector space». The Mathematical Gazette 60 (412): 115–117. doi:. https://archive.org/details/sim_mathematical-gazette_1976-06_60_412/page/n38.
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1, https://archive.org/details/solidstatephysic00ashc
- Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (2nd έκδοση), en:Addison-Wesley, ISBN 978-0-201-09394-0
- Atiyah, Michael Francis; Macdonald, Ian Grant (1969), Introduction to Commutative Algebra, Advanced Book Classics, en:Addison-Wesley
- Blass, Andreas (1984), «Existence of bases implies the axiom of choice», Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: en:American Mathematical Society, σελ. 31–33, ISBN 978-0-8218-5026-8, http://www.math.lsa.umich.edu/~ablass/bases-AC.pdf
- Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: en:Springer-Verlag, ISBN 978-3-540-64243-5
- Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1
- Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2nd έκδοση), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1
- Eisenberg, Murray; Guy, Robert (1979), «A proof of the hairy ball theorem», The American Mathematical Monthly 86 (7): 572–574, doi:
- Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94269-8
- Goldrei, Derek (1996), Classic Set Theory: A guided independent study (1st έκδοση), London: Chapman and Hall, ISBN 978-0-412-60610-6
- Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: en:Prentice Hall, ISBN 978-0-13-124405-4
- Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: en:Springer-Verlag, ISBN 978-0-387-90093-3
- Halpern, James D. (Jun 1966), «Bases in Vector Spaces and the Axiom of Choice», en:Proceedings of the American Mathematical Society 17 (3): 670–673, doi:
- Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M. (2013), Calculus : Single and Multivariable (6 έκδοση), en:John Wiley & Sons, ISBN 978-0470-88861-2
- Husemoller, Dale (1994), Fibre Bundles (3rd έκδοση), Berlin, New York: en:Springer-Verlag, ISBN 978-0-387-94087-8
- Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th έκδοση), Berlin, New York: en:Springer-Verlag, ISBN 978-3-540-25907-7
- Kreyszig, Erwin (1991), Differential geometry, New York: en:Dover Publications, σελ. xiv+352, ISBN 978-0-486-66721-8
- Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8th έκδοση), New York: en:John Wiley & Sons, ISBN 978-0-471-15496-9, https://archive.org/details/advancedengineer0008krey
- Luenberger, David (1997), Optimization by vector space methods, New York: en:John Wiley & Sons, ISBN 978-0-471-18117-0
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd έκδοση), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2
- Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0
- Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9
- Schönhage, A.; Strassen, Volker (1971), «Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)», Computing 7 (3–4): 281–292, doi:, ISSN 0010-485X
- Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish
- Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6, https://archive.org/details/galoistheory0000stewStewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 978-0-412-10800-6, https://archive.org/details/galoistheory0000stew
- Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Chapman and Hall, ISBN 978-0-13-535732-3
- Wallace, G.K. (Feb 1992), «The JPEG still picture compression standard», IEEE Transactions on Consumer Electronics 38 (1): xviii–xxxiv, doi:, ISSN 0098-3063, http://www.csc.ncsu.edu/faculty/rhee/export/papers/TheJPEGStillPictureCompressionStandard.pdf, ανακτήθηκε στις 2017-10-25
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ «3.1: Vector Spaces». Mathematics LibreTexts (στα Αγγλικά). 4 Φεβρουαρίου 2022. Ανακτήθηκε στις 5 Ιουλίου 2023.
- ↑ 2,0 2,1 2,2 2,3 Narici, Lawrence· Beckenstein, Edward (26 Ιουλίου 2010). Topological Vector Spaces. CRC Press. ISBN 978-1-58488-867-3.
- ↑ «ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ - Διανυσματικοί Χώροι (1) - ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ» (PDF).
- ↑ Frölicher, A.· Bucher, W. (15 Νοεμβρίου 2006). Calculus in Vector Spaces without Norm. Springer. ISBN 978-3-540-34862-7.
- ↑ Horvath, John (3 Οκτωβρίου 2013). Topological Vector Spaces and Distributions. Courier Corporation. ISBN 978-0-486-31103-6.
- ↑ Hausner, Melvin (17 Οκτωβρίου 2018). A Vector Space Approach to Geometry. Courier Dover Publications. ISBN 978-0-486-83539-6.
- ↑ Akcoglu, Mustafa A.· Bartha, Paul F. A. (9 Σεπτεμβρίου 2011). Analysis in Vector Spaces. John Wiley & Sons. ISBN 978-1-118-16459-4.
- ↑ «Στοιχεία Θεωρίας». myria.math.aegean.gr. Ανακτήθηκε στις 5 Ιουλίου 2023.
| ||||||||||||||||||||

































































































![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216)












































