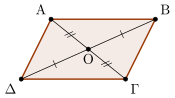
Παραλληλόγραμμο
Στην γεωμετρία, το παραλληλόγραμμο είναι ένα τετράπλευρο που έχει τις απέναντι πλευρές του παράλληλες.[1]:65[2]:89-93[3]:111[4]:97
Το σημείο τομής των διαγωνίων του λέγεται κέντρο του παραλληλογράμμου. Η απόσταση δύο απέναντι πλευρών παραλληλογράμμου λέγεται ύψος του ενώ οι απέναντι πλευρές λέγονται βάσεις ως προς το ύψος αυτό (κάθε παραλληλόγραμμο έχει δύο ύψη).
Ειδικές περιπτώσεις παραλληλογράμμου είναι το ορθογώνιο, ο ρόμβος και το τετράγωνο.
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
- Σε κάθε παραλληλόγραμμο οι απέναντι πλευρές είναι ίσες και οι απέναντι γωνίες είναι ίσες.[1]: 65 [2]: 90 [3]: 111,113
| Απόδειξη |
|
Θα ξεκινήσουμε δείχνοντας ότι οι απέναντι γωνίες είναι ίσες. Καθώς είναι παράλληλη στην προκύπτει ότι οι είναι παραπληρωματική της . Από την παραλληλία της και προκύπτει ότι οι και είναι παραπληρωματικές. Άρα (και αντίστοιχα .  Θεωρούμε την διαγώνιο . Τότε, έχουμε ότι ως εντός εναλλάξ και και η είναι κοινή. Επομένως, τα τρίγωνα και είναι ίσα. Επομένως, και . |
- Σε κάθε παραλληλόγραμμο οι διαγώνιοι διχοτομούνται.[2]: 91
| Απόδειξη |
 Έστω το σημείο τομής των διαγωνίων. Τα τρίγωνα και στο σχήμα είναι ίσα επειδή έχουν δύο ίσες γωνίες και την περιεχόμενη πλευρά τους ίση, συνεπώς και . |
- Το κέντρο ενός παραλληλογράμμου είναι κέντρο συμμετρίας του.
- Οι διχοτόμοι δύο απέναντι γωνιών είναι παράλληλες.[4]: 99
| Απόδειξη |
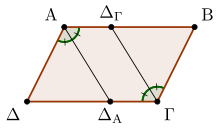 Από την παραλληλία των και έχουμε ότι . Αφού , έπεται ότι , και επομένως . |
| Απόδειξη |
 Έστω το σημείο τομής των δύο διχοτόμων. Τότε,
|
- Κριτήρια παραλληλογράμμου: Ένα κυρτό τετράπλευρο είναι παραλληλόγραμμο αν και μόνο αν ισχύει μία από τις παρακάτω προτάσεις:[1]: 66 [2]: 92-93 [3]: 113-115
- Οι απέναντι πλευρές είναι ίσες ανά δύο.
- Δύο απέναντι πλευρές είναι ίσες και παράλληλες.
- Οι απέναντι γωνίες είναι ίσες ανά δύο.
- Οι διαγώνιοί του διχοτομούνται.
Κριτήρια ισότητας παραλληλογράμμων[Επεξεργασία | επεξεργασία κώδικα]
Ισχύουν τα εξής κριτήρια ισότητας παραλληλογράμμων:[4]: 100-101
- Δύο παραλληλόγραμμα και με , και είναι ίσα.
- Δύο παραλληλόγραμμα και με , και είναι ίσα.
Μετρικές σχέσεις[Επεξεργασία | επεξεργασία κώδικα]
- (Νόμος του παραλληλογράμμου) Σε κάθε παραλληλόγραμμο το άθροισμα των τετραγώνων των πλευρών του είναι ίσο με το άθροισμα των τετραγώνων των διαγωνίων του,
- .
Εμβαδόν[Επεξεργασία | επεξεργασία κώδικα]

Υπάρχουν αρκετοί τύποι για το εμβαδόν του παραλληλογράμμου:
- Το εμβαδόν ισούται με το γινόμενο της βάσης και του αντίστοιχου ύψους:
- Από τον τύπο του Ήρωνα στο τρίγωνο , ισχύει ότι
- ,
- όπου και , και .
- Αν το σημείο , το και το , τότε
- .
Εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]

Θεώρημα Varignon[Επεξεργασία | επεξεργασία κώδικα]
Το θεώρημα Varignon λέει ότι τα μέσα των πλευρών ενός τετραπλεύρου , δημιουργούν ένα παραλληλόγραμμο.[5] Το παραλληλόγραμμο αυτό ονομάζεται το παραλληλόγραμμο Varignon.

Θεώρημα του Πάππου[Επεξεργασία | επεξεργασία κώδικα]
Το θεώρημα Πάππου για το εμβαδόν είναι ένα θεώρημα που συσχετίζεται τα εμβαδά τριών παραλληλογράμμων στις πλευρές ενός τριγώνου.
Σε αποδείξεις θεωρημάτων[Επεξεργασία | επεξεργασία κώδικα]
Σε αρκετές αποδείξεις θεωρημάτων βοηθάει η δημιουργία παραλληλογράμμων. Για παράδειγμα στην απόδειξη της ύπαρξης του βαρυκέντρου, στο θεώρημα van Schooten και στο θεώρημα Vecten.
Πλακοστρώσεις[Επεξεργασία | επεξεργασία κώδικα]
Τα παραλληλόγραμμα μπορούν να χρησιμοποιηθούν για να πλακοστρώσουν το επίπεδο.
Ειδικές περιπτώσεις[Επεξεργασία | επεξεργασία κώδικα]
Ένα παραλληλόγραμμο που έχει τις γωνίες του ορθές λέγεται ορθογώνιο παραλληλόγραμμο. Ένα παραλληλόγραμμο που έχει όλες του τις πλευρές ίσες λέγεται ρόμβος. Αν έχει και τις γωνίες του ορθές και τις πλευρές του ίσες, τότε λέγεται τετράγωνο.
Περαιτέρω ανάγνωση[Επεξεργασία | επεξεργασία κώδικα]
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Εφαρμογή για τα μήκη των πλευρών ενός παραλληλογράμμου
- Εφαρμογή με τις ιδιότητες του παραλληλογράμμου
Ελληνικά άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- Ν. Δεργιάδες (1979). «Συνθήκες για να είναι ένα κυρτό τετράπλευρο παραλληλόγραμμο». Ευκλείδης Β΄ (3): 108-110. http://www.hms.gr/apothema/?s=sa&i=3939.
- Α. Δούναβης (1986). «Παραλληλόγραμμα». Ευκλείδης Β΄ (2): 95-99. http://www.hms.gr/apothema/?s=sa&i=2995.
- Τ. Λαμπρόπουλος (1988). «Παραλληλόγραμμα». Ευκλείδης Β΄ (3): 24-28. http://www.hms.gr/apothema/?s=sa&i=3214.
Ξενόγλωσσα άρθρα[Επεξεργασία | επεξεργασία κώδικα]
- Scott, J. A. (Νοεμβρίου 2007). «91.68 Bridging parallelograms of equal area». The Mathematical Gazette 91 (522): 530–533. doi:. https://archive.org/details/sim_mathematical-gazette_2007-11_91_522/page/530.
- Hajja, Mowaffaq; Krasopoulos, Panagiotis T. (Μαρτίου 2023). «More characterisations of parallelograms». The Mathematical Gazette 107 (568): 76–83. doi:.
- Hajja, Mowaffaq; Krasopoulos, Panagiotis T. (Μαρτίου 2023). «More characterisations of parallelograms». The Mathematical Gazette 107 (568): 76–83. doi:.
- Wang, David G. L. (Σεπτεμβρίου 2016). «Tilings of Parallelograms by Similar Isosceles Triangles». The Mathematical Intelligencer 38 (3): 24–29. doi:.
- Daykin, D. E. (Ιανουαρίου 1965). «Rational Triangles and Parallelograms». Mathematics Magazine 38 (1): 46–47. doi:. https://archive.org/details/sim_mathematics-magazine_1965-01_38_1/page/46.
- Crain, Karleton W. (Απριλίου 1937). «Two Families of Parallelograms». National Mathematics Magazine 11 (7): 304. doi:.
- Mayor, F (Φεβρουαρίου 1941). «1499. Eighteen parallelograms». The Mathematical Gazette 25 (263): 46–47. doi:. https://archive.org/details/sim_mathematical-gazette_1941-02_25_263/page/46.<
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 1,2 Αλεξίου, Κ. Τ. (1975). Θεωρητική Γεωμετρία Τεύχος Α'. Αθήνα.
- ↑ 2,0 2,1 2,2 2,3 Νικολάου, Νικόλαος Δ. (1973). Θεωρητική Γεωμετρία. 1973: Οργανισμός εκδόσεως διδακτικών βιβλίων.
- ↑ 3,0 3,1 3,2 Τόγκας, Πέτρος Γ. (1957). Θεωρητική Γεωμετρία. Αθήνα: Πέτρου Γ. Τόγκα.
- ↑ 4,0 4,1 4,2 4,3 Ταβανλης, Χ. Επίπεδος Γεωμετρία 1. Ι. Χιωτέλη.
- ↑ Oliver, Peter N. (2001). «Pierre Varignon and the Parallelogram Theorem». The Mathematics Teacher 94 (4): 316–319. doi:. https://archive.org/details/sim_mathematics-teacher_2001-04_94_4/page/316.