Διάσταση
Γενικά διάσταση ονομάζεται η απόσταση μεταξύ δύο οριακών σημείων και συνεκδοχικά η οποιαδήποτε ενάντια θέση. Η λέξη προέρχεται από το διαστῆναι,[1] απαρέμφατο αορίστου β' του αρχαιοελληνικού ρήματος διίστημι, που σημαίνει τοποθετούμαι χωριστά, στέκομαι ενάντια, ξεχωρίζω, διαχωρίζομαι.[2] Στα νομικά, είναι η κατάσταση κατά την οποία το αντρόγυνο ζει χωριστά χωρίς να έχει πάρει διαζύγιο, όπως στη φράση: "εν διαστάσει" βίος έναντι τού πρότερου έγγαμου. Άλλοτε δείχνει την διαφορά γνώμης, όπως: Υπήρξε σοβαρή διάσταση απόψεων μεταξύ των δύο. Ακόμα δείχνει το μέγεθος γεγονότων, όπως: σκάνδαλο (ή πυρκαγιά, απεργία κ.λπ.) σε κλίμακα μεγάλων διαστάσεων.
Στη Γεωμετρία[Επεξεργασία | επεξεργασία κώδικα]
Στη γεωμετρία οι διαστάσεις αφορούν τα μετρήσιμα μεγέθη του χώρου που καταλαμβάνει ένα γεωμετρικό σχήμα. Υπό αυτή την έννοια υπάρχει η διάσταση του μήκους, που είναι η απόσταση σημείου από σημείο, του πλάτους, που είναι κάθετη απόσταση στο μήκος και δίδεται έτσι η έννοια του επιπέδου καθώς και του ύψους, που είναι η κάθετη απόσταση σε επίπεδο και προσδιορίζεται ως τρίτη διάσταση των στερεών και του χώρου. Εξ αυτών θεωρείται ότι γενικά ο χώρος έχει τρεις διαστάσεις: το μήκος, το πλάτος και το ύψος.
Στη διαφορική γεωμετρία ερευνώνται επίσης στο χώρο οι ν διαστάσεις που είναι όμως κατασκευάσματα της ανθρώπινης λογικής, και οι οποίες δεν υποπίπτουν στην ανθρώπινη αντίληψη. Έτσι αν τη λέξη χώρος την παραστήσουμε με το λατινικό γράμμα R τότε το "σημείο" (επειδή δεν έχει διαστάσεις) παρίσταται ως R0 και αποκαλείται "χώρος μηδενικής διάστασης". Η δε γραμμή = R1, ως "χώρος μιας διάστασης", το επίπεδο = R2 ως "χώρος δύο διαστάσεων" και ο όγκος = R3, ως "χώρος τριών διαστάσεων".
Στη Σχετικότητα[Επεξεργασία | επεξεργασία κώδικα]

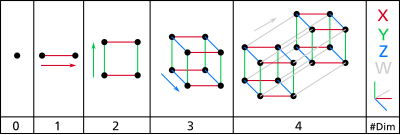
1: Δύο σημεία Α και Β μπορεί να συνδεθούν με μία γραμμή, δίνοντας ένα νέο ευθύγραμμο τμήμα ΑΒ.
2: Δύο παράλληλα ευθύγραμμα τμήματα ΑΒ και ΓΔ μπορούν να συνδεθούν για να γίνει ένα τετράγωνο ΑΒΓΔ.
3: Δύο παράλληλα τετράγωνα ΑΒΓΔ και ΕΖΗΘ μπορούν να συνδεθούν για να γίνει ένας κύβος ΑΒΓΔΕΖΗΘ.
4: Δύο παράλληλοι κύβοι ΑΒΓΔΕΖΗΘ και ΙΚΛΜΝΞΟΠ μπορούν να συνδεθούν για να γίνει ένα τεσσεράκτιο ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠ.
Κατά τη Θεωρία της σχετικότητας οι τρεις διαστάσεις του στερεού εξαρτώνται και από την κίνησή του στον χώρο. Κατ΄ αυτή την έννοια υφίσταται η τέταρτη διάσταση στο χώρο του R4, που λέγεται και "χώρος τεσσάρων διαστάσεων" (στη σχετικότητα η διάσταση αυτή είναι ο χρόνος).
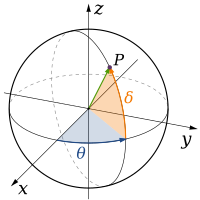
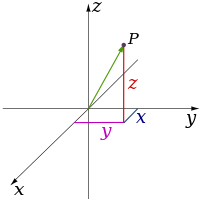
Στη φυσική και τα μαθηματικά, η διάσταση ενός χώρου ή αντικειμένου ανεπίσημα, ορίζεται ως ο ελάχιστος αριθμός των συντεταγμένων που απαιτούνται για να καθοριστεί οποιοδήποτε σημείο μέσα σε αυτό. Έτσι, μια γραμμή έχει μία διάσταση, διότι μόνο μία συντεταγμένη είναι απαραίτητη για να προσδιορίζει ένα σημείο σχετικά με αυτό (για παράδειγμα, το σημείο 5 σε μια αριθμημένη γραμμή). Μία επιφάνεια, όπως ένα αεροπλάνο ή η επιφάνεια ενός κυλίνδρου ή σφαίρας, έχει δύο διαστάσεις, επειδή δύο συντεταγμένες χρειάζονται για να καθορίσετε ένα σημείο σε αυτά (για παράδειγμα, για να εντοπίσετε ένα σημείο στην επιφάνεια μιας σφαίρας, θα πρέπει να έχετε τόσο το γεωγραφικό πλάτος, όσο και το γεωγραφικό μήκος του). Το εσωτερικό ενός κύβου, ενός κυλίνδρου ή μιας σφαίρας είναι τρισδιάστατο επειδή τρεις συντεταγμένες χρειάζονται για να εντοπίσετε ένα σημείο μέσα σε αυτούς τους χώρους. Στη φυσική, η διάσταση αναφέρεται στη συστατική δομή όλων των χώρων (βλ. όγκος) και τη θέση της στο χρόνο (που είναι αντιληπτή ως μια διάσταση κατά μήκος του άξονα t), επίσης και η χωρική συγκρότηση των αντικειμένων εντός των χώρων (οι δομές που σχετίζονται ταυτόχρονα με τις έννοιες των σωματιδίων και του χώρου, αλληλεπιδρούν με τις σχετικές ιδιότητες της μάζας) και στην περιγραφή τους είναι βασικά σαν μαθηματικές έννοιες. Αυτοί, ή άλλοι άξονες μπορούν να χρησιμοποιηθούν για να ταυτοποιήσουμε μοναδικά ένα σημείο (ή μια δομή σε κάποια στάση της) και τη σχέση του με άλλα αντικείμενα ή μορφές. Φυσικές θεωρίες που συμπεριλαμβάνουν το χρόνο, όπως η γενική θεωρία της σχετικότητας, θεωρούνται ότι δουλεύουν στον 4-διάστατο «χωροχρόνο» (που ορίζεται και ως χώρος Minkowski). Οι μοντέρνες θεωρίες τείνουν να είναι «πολύ-διάστατες» και περιλαμβάνουν την θεωρία κβαντικού πεδίου και τη θεωρία των χορδών. Η δήλωση του χώρου στην κβαντομηχανική είναι ένας λειτουργικός χώρος απείρων διαστάσεων. Η έννοια της διάστασης δεν περιορίζεται σε φυσικά αντικείμενα. Οι πολυδιάστατοι χώροι υπάρχουν στα μαθηματικά και γενικότερα στις επιστήμες για πολλούς λόγους, συχνά ως χώροι διαμόρφωσης όπως η Χαμιλτονιανή ή Λαγκρανζιανή μηχανική. Αυτοί οι αφηρημένοι χώροι είναι ανεξάρτητοι του φυσικού χώρου στον οποίο ζούμε.
Στα μαθηματικά[Επεξεργασία | επεξεργασία κώδικα]
Στα μαθηματικά, η διάσταση ενός αντικειμένου είναι εγγενής, ανεξάρτητη ιδιοκτησία του χώρου στον οποίο το αντικείμενο είναι ενσωματωμένο. Για παράδειγμα, ένα σημείο του μοναδιαίου κύκλου στο επίπεδο μπορεί να οριστεί από δύο Καρτεσιανές συντεταγμένες, αλλά μπορεί να γίνει και μόνο με μία συντεταγμένη (την πολική συντεταγμένη γωνίας) οπότε ο κύκλος είναι μονοδιάστατος παρόλο που υπάρχει στο δισδιάστατο πεδίο. Αυτή η εγγενής κατανόηση της διάστασης είναι από τους κυριότερους τρόπους, με τους οποίους η μαθηματική έννοια της διάστασης διαφέρει από την κοινή χρήση του όρου.
Οι διαστάσεις του Ευκλείδειου n-χώρου En είναι n. Όταν προσπαθούμε να γενικεύσουμε άλλους τύπους του χώρου, βρισκόμαστε αντιμέτωποι με την ερώτηση «τι κάνει το En n-διάστατο;» Μια απάντηση είναι να καλύψουμε μία πεπερασμένη μπάλα στο En με μικρότερες μπάλες ακτίνος ε, έτσι θα χρειαζόταν κάποιος μια σειρά από εn τέτοιες μικρές μπάλες. Αυτή η παρατήρηση μας οδηγεί στον ορισμό της διάστασης Μινκόφσκι και της πιο εξελιγμένης μορφής της, την διάσταση Χάουσντορφ, ενώ παράλληλα υπάρχουν και άλλες πιθανές απαντήσεις στην παραπάνω ερώτηση. Για παράδειγμα, τα όρια μιας μπάλας στο En μοιάζουν σε τοπικό επίπεδο, με του En-1 και αυτό οδηγεί στην έννοια της επαγωγικής διάστασης. Αν και αυτές οι έννοιες συμφωνούν στο En, αποδεικνύεται πως διαφοροποιούνται όταν οι χώροι γενικεύονται.
Ένα τεσσεράκτιο (ή κανονικό οκτάχωρο) είναι ένα παράδειγμα τετραδιάστατου αντικειμένου. Ενώ εκτός των μαθηματικών η έκφραση για την διάσταση είναι: «Το τεσσεράκτιο έχει τέσσερις διαστάσεις», στα μαθηματικά οι συνήθεις εκφράσεις είναι «Το τεσσεράκτιο έχει διάσταση 4» ή «Η διάσταση του τεσσερακτίου είναι 4».
Παρά το γεγονός ότι η έννοια των υψηλότερων διαστάσεων πηγαίνει πίσω μέχρι τον Ρενέ Ντεκάρτ, η ουσιαστική εξέλιξη πάνω στην γεωμετρία πολλών διαστάσεων ξεκίνησε μόλις τον 19ο αιώνα, με το έργο των Άρθουρ Κέιλι, Γουίλιαμ Ρόουαν Χάμιλτον, Λούντβιχ Σλάφλι και Μπέρναρντ Ρίμαν. Το "Habilitationsschrift" του Ρίμαν το 1854, η "Theorie der vielfachen Kontinuität" του Σλάφλι το 1852, η ανακάλυψη των των "quaternions" του Χάμιλτον το 1843 και η κατασκευή της Άλγεβρας Κέιλι σηματοδότησαν την αρχή της γεωμετρίας πολλών διαστάσεων.
Η υπόλοιπη ενότητα εξετάζει κάποιους από τους πιο σημαντικούς μαθηματικούς ορισμούς των διαστάσεων.
Διάσταση ενός διανυσματικού χώρου[Επεξεργασία | επεξεργασία κώδικα]
Η διάσταση ενός διανυσματικού χώρου είναι ο αριθμός των διανυσμάτων σε οποιαδήποτε βάση για το χώρο, δηλαδή ο αριθμός των συντεταγμένων που είναι αναγκαίες για να διευκρινιστεί κάθε φορέας. Αυτή η έννοια της διάστασης (η πληθάριθμος της βάσης) συχνά αναφέρεται ως Hamel διάσταση ή αλγεβρική διάσταση για να τη διακρίνουν από τις άλλες έννοιες της διάστασης.
Πολλαπλές[Επεξεργασία | επεξεργασία κώδικα]
Μια συνδεδεμένη τοπολογική πολλαπλή είναι τοπικά ομοιομορφική με την Ευκλείδειο n-χώρο, και ο αριθμός n λέγεται διάσταση του συλλέκτη. Κάποιος μπορεί να δείξει ότι αυτό δίνει μια μοναδική διάσταση που ορίζεται για κάθε συνδεδεμένη τοπολογική πολλαπλή.
Για συνδεδεμένες Διαφορίσιμες πολλαπλότητες η διάσταση είναι επίσης η διάσταση της εφαπτομένης διανυσματικού διαστήματος σε οποιοδήποτε σημείο.
Η θεωρία των πολλαπλοτήτων, στον τομέα της γεωμετρικής τοπολογίας, χαρακτηρίζεται παρεμπιπτόντως με διαστάσεις 1 και 2, που είναι σχετικά στοιχειώδεις, οι υψηλές διαστάσεις στην περίπτωση n > 4 είναι απλοποιημένες, έχοντας επιπλέον χώρο στον οποίο να "λειτουργούν". Και οι περιπτώσεις n = 3 και n = 4 είναι, υπό ορισμένες συνθήκες, οι πιο δύσκολες. Η κατάσταση αυτή ήταν ιδιαίτερα έντονη στις διάφορες περιπτώσεις των εικασιών του Πουανκαρέ, όπου εφαρμόζει τέσσερις διαφορετικές μεθόδους απόδειξης.
Ποικιλίες[Επεξεργασία | επεξεργασία κώδικα]
Η διάσταση μιας αλγεβρικής ποικιλίας μπορεί να οριστεί με διάφορους ισοδύναμους τρόπους. Ο πιο έξυπνος τρόπος είναι ίσως η διάσταση της εφαπτομένης χώρου σε οποιοδήποτε κανονικό σημείο. Ένας άλλος διαισθητικός τρόπος είναι να καθοριστεί η διάσταση καθώς και ο αριθμός των υπερεπίπεδων που απαιτούνται ώστε να έχουν μια τομή με την ποικιλία που μειώνεται σε ένα πεπερασμένο αριθμό σημείων (διάσταση μηδέν). Ο ορισμός αυτός βασίζεται στο γεγονός ότι η τομή μιας ποικιλίας με ένα υπερεπίπεδο μειώνει τη διάσταση εκτός αν το υπερεπίπεδο περιέχει την ποικιλία. Ένα αλγεβρικό σύνολο είναι μια πεπερασμένη ένωση από αλγεβρικές ποικιλίες και η διάσταση είναι η μέγιστη από τις διαστάσεις των συνιστωσών του. Είναι ίση με το μέγιστο μήκος των αλυσίδων των επιμέρους ποικιλιών της συγκεκριμένης ποικιλίας (το μήκος μιας τέτοιας αλυσίδας είναι ο αριθμός των "").
Διάσταση Krull[Επεξεργασία | επεξεργασία κώδικα]
Η διάσταση Krull ενός αντιμεταθετικού δακτυλίου είναι το μέγιστο μήκος των αλυσίδων των πρωταρχικών ιδανικών σε αυτό, μια αλυσίδα μήκους n είναι μια ακολουθία πρωταρχικών ιδανικών που σχετίζονται με την ένταξη. Είναι στενά συνδεδεμένη με την διάσταση μιας αλγεβρικής ποικιλίας, λόγω της φυσικής αντιστοιχίας μεταξύ των επιμέρους ποικιλιών καθώς και των πρωταρχικών ιδανικών του δακτυλίου των πολυωνύμων με την ποικιλία.
Για την άλγεβρα πάνω σε πεδίο, η διάσταση ως διανυσματικός χώρος είναι πεπερασμένη αν και μόνον αν η Krull διάσταση είναι 0.
Διάσταση κάλυψης[Επεξεργασία | επεξεργασία κώδικα]
Επίσης γνωστή ως διάσταση κάλυψης Lebesgue ή τοπολογική διάσταση[3] Για οποιοδήποτε κανονικό τοπολογικό χώρο Χ, ο Lebesgue καλύπτει την διάσταση Χ που ορίζεται να είναι n, αν n είναι ο μικρότερος ακέραιος για τον οποίο ισχύουν τα παρακάτω: κάθε ανοικτό κάλυμμα έχει μια ανοικτή τελειοποίηση (ένα δεύτερο ανοικτό κάλυμμα, όπου κάθε στοιχείο είναι ένα υποσύνολο ενός στοιχείου στο πρώτο κάλυμμα) έτσι ώστε κανένα σημείο να μην περιλαμβάνεται σε περισσότερα από n + 1 στοιχεία. Στην περίπτωση αυτή, dim X = n. Για X ενός συλλέκτη, αυτή συμπίπτει με τη διάσταση που αναφέρεται παραπάνω. Εάν δεν υπάρχει τέτοιος ακεραίος n, τότε υπάρχει η διάσταση Χ και λέγεται ότι είναι άπειρη, και γράφεται Χ = ∞. Επιπλέον, η διάσταση Χ είναι -1, δηλαδή dim Χ = -1 αν και μόνο αν το Χ είναι άδειο. Αυτός ο ορισμός της κάλυψης διάστασης μπορεί να παραταθεί από την τάξη των κανονικών χώρων σε όλους τους χώρους Τιχόνοφ (Tychonoff) απλώς με αντικατάσταση του όρου "ανοιχτό" στον ορισμό του όρου "συναρτησιακά ανοικτό".
Επαγωγική διάσταση[Επεξεργασία | επεξεργασία κώδικα]
Ένας επαγωγικός ορισμός της διάστασης μπορεί να δημιουργηθεί ως εξής. Εξετάστε ένα διακριτό σύνολο σημείων (όπως μια πεπερασμένη συλλογή σημείων) να είναι 0-διαστάσεων. Σύροντας ένα 0-διαστάσεων αντικείμενο προς κάποια κατεύθυνση, επιτυγχάνεται ένα 1-διαστάσεων αντικείμενο. Σύροντας ένα 1-διαστάσεων αντικείμενο προς μια νέα κατεύθυνση, λαμβάνεται ένα 2-διαστάσεων αντικείμενο. Σε γενικές γραμμές με το σύρσιμο ενός ν-διάστατου αντικείμενου προς μία νέα κατεύθυνση, λαμβάνεται ένα (ν+1)-διαστάσεων αντικείμενο. Η επαγωγική διάσταση ενός τοπολογικού χώρου μπορεί να παραπέμψει στη μικρή επαγωγική διάσταση ή τη μεγάλη επαγωγική διάσταση, και βασίζεται στην αναλογία ότι (ν+1)-διαστάσεων μπάλες έχουν ν διαστάσεων όρια, επιτρέποντας ένα επαγωγικό ορισμό που βασίζεται στη διάσταση των ορίων των ανοικτών συνόλων.
Διάσταση Χάουσντορφ[Επεξεργασία | επεξεργασία κώδικα]
Για δομικά πολύπλοκα σύνολα, ειδικά τα φράκταλ, η διάσταση Χάουσντορφ είναι χρήσιμη. Η διάσταση Χάουσντορφ ορίζεται για όλους τους μετρικούς χώρους και, σε αντίθεση με τη διάσταση Χάμελ, μπορεί να επιτύχει και σε μη-ακέραιες πραγματικές τιμές. Η διάσταση Μινκόφσκι (ή διάσταση box-counting) είναι μια παραλλαγή της ίδιας ιδέας. Σε γενικές γραμμές, υπάρχουν περισσότεροι ορισμοί των φράκταλ διαστάσεων που εργάζονται για πολύ ακανόνιστα σύνολα και την επίτευξη των μη-ακέραιων θετικών πραγματικών τιμών. Τα φράκταλ έχουν βρεθεί χρήσιμα για να περιγράψουν πολλά φυσικά αντικείμενα και φαινόμενα. Η διάσταση αυτή είναι επίσης γνωστή και ως διάσταση φράκταλ.[4]
Χώροι Χίλμπερτ[Επεξεργασία | επεξεργασία κώδικα]
Κάθε χώρος Χίλμπερτ δέχεται μια ορθοκανονική βάση, και κάθε δύο τέτοιες βάσεις για ένα συγκεκριμένο χώρο έχουν τoν ίδιo πληθάριθμο. Αυτός ο πληθάριθμος ονομάζεται η διάσταση του χώρου Χίλμπερτ. Η διάσταση αυτή είναι πεπερασμένη αν και μόνο αν η διάσταση Χάμελ του χώρου είναι πεπερασμένη, και σε αυτή την περίπτωση οι παραπάνω διαστάσεις συμπίπτουν.
Στη φυσική[Επεξεργασία | επεξεργασία κώδικα]
Χωρικές διαστάσεις[Επεξεργασία | επεξεργασία κώδικα]
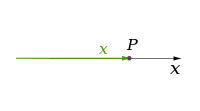
Κλασσικές θεωρίες της φυσικής περιγράφουν τρεις φυσικές διαστάσεις: από ένα συγκεκριμένο σημείο στο χώρο, οι βασικές κατευθύνσεις στις οποίες μπορούμε να προχωρήσουμε είναι πάνω ή κάτω, αριστερά ή δεξιά και προς τα εμπρός ή πίσω. Η κίνηση σε οποιαδήποτε άλλη κατεύθυνση μπορεί να εκφραστεί με τον καθορισμό αυτών ακριβώς των τριών συντεταγμένων. Η κίνηση προς τα κάτω, είναι η ίδια με την κίνηση προς τα πάνω μιας αρνητικής απόστασης. Μετακίνηση διαγώνια προς τα πάνω και προς τα εμπρός καθορίζεται ακριβώς με το όνομα της κατεύθυνσης που συνεπάγεται. Δηλαδή, κινείται σε ένα γραμμικό συνδυασμό προς τα πάνω και εμπρός. Στην απλούστερη μορφή του: μια γραμμή περιγράφει μία διάσταση, ένα επίπεδο περιγράφει δύο διαστάσεις, και ένας κύβος περιγράφει τρεις διαστάσεις. (Βλέπε διάστημα και καρτεσιανό σύστημα συντεταγμένων.)
| Διαστάσεις | Παραδείγματα συστημάτων συντεταγμένων | |||
|---|---|---|---|---|
| Μία |
| |||
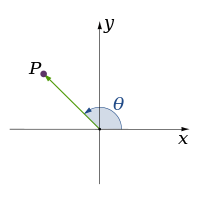
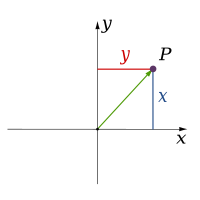
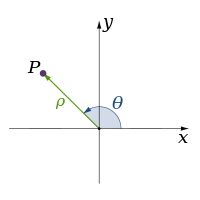
| Δύο |
| |||
| Τρεις |
|
Χρόνος[Επεξεργασία | επεξεργασία κώδικα]
Μια χρονική διάσταση είναι η διάσταση του χρόνου. Για το λόγο αυτό ο χρόνος συχνά αναφέρεται ως η "τέταρτη διάσταση", αυτό δεν υπονοεί όμως ότι είναι μια χωρική διάσταση. Η χρονική διάσταση είναι ένας τρόπος για να μετρηθεί μια φυσική μεταβολή. Αντίθετα με τις τρεις χωρικές διαστάσεις, στον χρόνο γίνεται αντιληπτό ότι υπάρχει μόνο μία διάσταση, διότι δεν μπορείς να κινηθείς ελεύθερα στο χρόνο και ουσιαστικά μπορείς να κινηθείς μόνο προς μία κατεύθυνση.
Οι εξισώσεις που χρησιμοποιούνται στη φυσική δεν αντιμετωπίζουν στην πραγματικότητα τον χρόνο με τον ίδιο τρόπο που συνήθως τον αντιλαμβάνονται οι άνθρωποι. Οι εξισώσεις της κλασικής μηχανικής είναι συμμετρικές ως προς το χρόνο, ενώ στις εξισώσεις της κβαντικής μηχανικής είναι τυπικά συμμετρικές, όταν τόσο ο χρόνος όσο και οι άλλες ποσότητες (όπως το φορτίο και το parity) αντιστρέφονται. Σε αυτά τα μοντέλα, η αντίληψη του χρόνου που ρέει σε μια κατεύθυνση είναι ένα κατασκεύασμα των νόμων της θερμοδυναμικής (αντιλαμβανόμαστε τον χρόνο καθώς αυτός ρέει προς την κατεύθυνση της αύξησης της εντροπίας).
Η πιο γνωστή αντιμετώπιση του χρόνου ως διάσταση είναι του Πουανκαρέ και η ειδική θεωρία της σχετικότητας του Αϊνστάιν (που επεκτάθηκε με τη γενική σχετικότητα), η οποία αντιμετωπίζει και αντιλαμβάνεται τον χώρο και τον χρόνο ως συστατικά ενός τεσσάρων διαστάσεων πολυειδές, που είναι γνωστό ως χωροχρόνος, και στην ειδική, ως χώρο Minkowski κατ' υπόθεση.
Πρόσθετες διαστάσεις[Επεξεργασία | επεξεργασία κώδικα]
Στη φυσική, οι τρεις διαστάσεις του χώρου και η μία του χρόνου είναι ο αποδεκτός κανόνας. Ωστόσο, υπάρχουν θεωρίες που προσπαθούν να ενοποιήσουν τις θεμελιώδεις δυνάμεις με την εισαγωγή περισσότερων διαστάσεων. Η θεωρία υπερχορδών, η Θεωρία-Μ και η θεωρία χορδής μποζονίων, αντίστοιχα, θεωρούν δεδομένο ότι ο φυσικός χώρος έχει 10, 11 και 26 διαστάσεις. Αυτές οι πρόσθετες διαστάσεις λέγεται ότι είναι χωρικές. Ωστόσο, αντιλαμβανόμαστε μόνο τρεις χωρικές διαστάσεις μέχρι σήμερα. Μια πιθανή εξήγηση που έχει προταθεί είναι ότι ο χώρος λειτουργεί σε υποατομικό επίπεδο, ενδεχομένως στο επίπεδο της κλίμακας της Κουάρκ/χορδής ή κάτω από αυτό.
Μια ανάλυση των αποτελεσμάτων από το Large Hadron Collider το Δεκέμβριο του 2010 περιορίζει σοβαρά τις θεωρίες με μεγάλες πρόσθετες διαστάσεις.
Άλλες φυσικές θεωρίες που έχουν εισαχθεί για επιπλέον διαστάσεις του χώρου είναι:
- Η "Kaluza-Klein θεωρία" εισάγει επιπλέον διαστάσεις για να εξηγήσει τις θεμελιώδεις δυνάμεις εκτός της βαρύτητας (αρχικά μόνο του ηλεκτρομαγνητισμού).
- Η "Μεγάλη επιπλέον διάσταση" και το μοντέλο "Randall-Sundrum" προσπαθούν να εξηγήσουν την αδυναμία της βαρύτητας. Αυτό είναι επίσης ένα χαρακτηριστικό της κοσμολογίας βράνης.
- Η "Συμπαντική επιπλέον διάσταση".
Δίκτυα και διαστάσεις[Επεξεργασία | επεξεργασία κώδικα]
Μερικά σύνθετα δίκτυα χαρακτηρίζονται από φράκταλ διαστάσεις. Η έννοια της διάστασης μπορεί να γενικευθεί στο να περιλαμβάνονται δίκτυα ενσωματωμένα στο χώρο. Η διάσταση χαρακτηρίζεται ως προς τους χωρικούς περιορισμούς της.
Φιλοσοφία[Επεξεργασία | επεξεργασία κώδικα]
Το 1783, ο Εμμάνουελ Καντ έγραψε: «Το γεγονός ότι υπάρχει παντού χώρος (ο οποίος δεν είναι το όριο κάποιου άλλου χώρου) που έχει τρεις διαστάσεις και ότι ο χώρος σε γενικές γραμμές δεν μπορεί να έχει περισσότερες διαστάσεις, βασίζεται στην άποψη ότι δεν είναι περισσότερες από τρεις γραμμές αυτές που μπορούν να τέμνονται με ορθές γωνίες σε ένα σημείο. Αυτή η πρόταση δεν μπορεί να αποδειχθεί από τις έννοιες καθόλου, αλλά στηρίζεται άμεσα στη διαίσθηση και μάλιστα σε καθαρή διαίσθηση διότι είναι εκ των προτέρων αποδεδειγμένα ορισμένες».
«Ο χώρος έχει τέσσερις διαστάσεις», είναι μια μικρή ιστορία που δημοσιεύθηκε το 1846 από τον Γερμανό φιλόσοφο και πειραματικό ψυχολόγο Γκούσταβ Φέχνερ (με το ψευδώνυμο Dr Mises). Ο πρωταγωνιστής της ιστορίας είναι μια σκιά που γνωρίζει άλλες σκιές και είναι σε θέση να επικοινωνεί μαζί τους, αλλά είναι παγιδευμένος σε μια δισδιάστατη επιφάνεια. Σύμφωνα με τον Fechner, ο άνθρωπος σκιά θα συλλαμβάνει την τρίτη διάσταση ως ένα χρόνο. Η ιστορία φέρει μεγάλη ομοιότητα με την Αλληγορία του Σπηλαίου, που παρουσιάζεται στον Πλάτωνα και η οποία γράφτηκε το 380 π.Χ. περίπου.
Το 1898 ο Σιμόν Νιούκομπ έγραψε ένα άρθρο για το Δελτίο της Αμερικανικής Μαθηματικής Εταιρείας με τίτλο «Η Φιλοσοφία του Υπερχώρου». Το 1983 η Linda Dalrymple Henderson στη διατριβή της για την "τέταρτη διάσταση στην τέχνη κατά τις αρχές του εικοστού αιώνα" επινόησε τον φιλοσοφικό όρο "Hyperspace" (Υπερχώρος ή Υπερδιάστημα), ο οποίος χρησιμοποιείται για να περιγράψει εκείνες τις συγγραφές που χρησιμοποιούν υψηλότερες διαστάσεις για μεταφυσική και φιλοσοφική έρευνα. Ο Τσαρλς Χάουαρντ Χίντον, ο οποίος το 1888 ήταν ο πρώτος που χρησιμοποίησε τη λέξη "tesseract" (Τεσσεράκτιο), και ο Ρώσος εσωτεριστής Π. Δ. Ουσπένσκυ είναι παραδείγματα των φιλοσόφων του "Υπερχώρου".
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Βλ. λήμματα «διάστασις» και «διάστημα», στο Μέγα λεξικόν της Ελληνικής γλώσσης. Α΄α. Αθήνα: Εκ του τυπογραφείου των καταστημάτων Ανέστη Κωνσταντινίδη. 1901. σελ. 606.
- ↑ Βλ. λήμμα «διίστημι», Henry George Liddell, Robert Scott: A Greek-English Lexicon (1889). Perseus Digital Library - Tufts University. Ανακτήθηκε στις 11-10-2016.
- ↑ Weisstein, Eric W., "Lebesgue Covering Dimension" από το MathWorld.
- ↑ Weisstein, Eric W., "Dimension" από το MathWorld.
Περαιτέρω διάβασμα[Επεξεργασία | επεξεργασία κώδικα]
- Edwin A. Abbott (1884), Flatland: A Romance of Many Dimensions, Public Domain. Online version with ASCII approximation of illustrations at Project Gutenberg.
- Thomas Banchoff (1996), Beyond the Third Dimension: Geometry, Computer Graphics, and Higher Dimensions, Second Edition, Freeman.
- Michio Kaku (1994), Hyperspace, a Scientific Odyssey Through the 10th Dimension, Oxford University Press.
- Clifford A. Pickover (1999), Surfing through Hyperspace: Understanding Higher Universes in Six Easy Lessons, Oxford University Press.
- Rudy Rucker (1984), The Fourth Dimension, Houghton-Mifflin.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Copeland, Ed (2009). «Extra Dimensions». Sixty Symbols. Brady Haran for the University of Nottingham.
| ||||||||||||||||||||