Δισδυάκις τριακοντάεδρο

Δισδυάκις τριακοντάεδρο
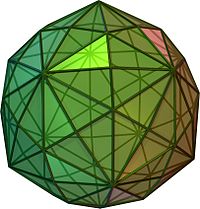(κινούμενο μοντέλο)
Τύπος	Καταλανικό στερεό
Έδρες	120 σκαληνά τρίγωνα
Ακμές	180
Κορυφές	62
Ομάδα συμμετρίας	εικοσαεδρική (Ih)
Δυϊκό	Κόλουρο εικοσιδωδεκάεδρο
Ανάπτυγμα

Στη Στερεομετρία, το δισδυάκις τριακοντάεδρο (ή εξάκις εικοσάεδρο) είναι ένα κυρτό πολύεδρο, που ανήκει στα καταλανικά στερεά, τα οποία είναι δυϊκά των αρχιμήδειων στερεών. Συγκεκριμένα, το δισδυάκις τριακοντάεδρο είναι το δυϊκό του κόλουρου εικοσιδωδεκάεδρου. Διαθέτει 120 έδρες σχήματος σκαληνού τριγώνου.

Ανάμεσα σε όλα τα κυρτά πολύεδρα των οποίων οι έδρες είναι ίσες μεταξύ τους και με εξαίρεση τις διπυραμίδες και τα τραπεζόεδρα, το δισδυάκις τριακοντάεδρο είναι αυτό που έχει τις περισσότερες έδρες.

Γεωμετρικά χαρακτηριστικά

Δεδομένου ότι οι έδρες του στερεού είναι σκαληνά τρίγωνα, αυτό σημαίνει ότι οι ακμές του είναι τριών ειδών. Αν λάβουμε το μήκος της ακμής του δυϊκού κόλουρου εικοσιδωδεκάεδρου ίσο με τη μονάδα, τότε το μήκος των ακμών του δισδυάκις τριακοντάεδρου είναι s₁ $=$ 1/11√15(85$-$31√5), s₂ $=$ 3/55√15(65$+$19√5) και s₃ $=$ 2/5√15(5$-$√5).

Τώρα, αν θεωρήσουμε το μήκος της μικρότερης ακμής (s₁) του στερεού ίσο με τη μονάδα, τότε ισχύουν τα εξής:

Συνολική επιφάνεια	$S={\frac {3}{5}}{\sqrt {10(1257+541{\sqrt {5}})}}\approx 94,235$
Όγκος	$V={\frac {1}{5}}{\sqrt {6(14765+6602{\sqrt {5}})}}\approx 84,182$

Αν προβληθούν σε μια σφαίρα οι ακμές του δισδυάκις τριακοντάεδρου, σχηματίζουν στην επιφάνειά της 15 μέγιστους κύκλους.

Πηγές

• (Αγγλικά) Weisstein, Eric W., Disdyakis Triacontahedron στο MathWorld
• (Αγγλικά) disdyakis triacontahedron στο Wolfram Alpha