Επτάγωνο

Στη γεωμετρία, το επτάγωνο (από τις ελληνικές λέξεις επτά και γωνία) είναι πολύγωνο σχήμα με επτά πλευρές και επτά κορυφές. Σε ένα κανονικό επτάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους, οι γωνίες είναι ίσες με 5π/7 ακτίνια ή 128,5714286 μοίρες (°) η καθεμιά, ενώ οι εσωτερικές γωνίες οποιουδήποτε επταγώνου έχουν άθροισμα 5π ακτίνια ή 900 μοίρες ακριβώς. Το σύμβολο Schläfli του επταγώνου είναι {7}.

Το εμβαδό (Ε) ενός κανονικού επταγώνου με μήκος πλευράς α δίνεται από τη σχέση:

$E={\frac {7}{4}}a^{2}\cot {\frac {\pi }{7}}\simeq 3,633912444a^{2}.$

Κατασκευή

Το κανονικό επτάγωνο δεν είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη. Μπορεί να κατασκευασθεί με τη μέθοδο της νεύσης και την κατασκευή αυτή παρουσιάζει ο Αρχιμήδης στο σωζόμενο έργο του Περί του κανονικού επταγώνου. Είναι επίσης κατασκευάσιμο με κανόνα και διαβήτη και τριχοτομητή γωνίας. Η αδυναμία κατασκευής του κανονικού επταγώνου με κανόνα και διαβήτη έπεται από το γεγονός ότι ο αριθμός $\scriptstyle {2\cos {\tfrac {2\pi }{7}}\approx 1,247}$ είναι μία ρίζα του μη αναγώγιμου κυβικού πολυωνύμου x³ + x² − 2x − 1. Συνεπώς αυτό το πολυώνυμο είναι το minimal πολυώνυμο του 2cos(^2π⁄₇), ενώ ο βαθμός του minimal πολυωνύμου για έναν κατασκευάσιμο αριθμό πρέπει να είναι μια δύναμη του 2.

Μία κατασκευή με νεύσιν της εσωτερικής γωνίας ενός κανονικού επταγώνου.	Μία κατασκευή με νεύσιν της εσωτερικής γωνίας ενός κανονικού επταγώνου από τον John Horton Conway.
Μία προσεγγιστική κατασκευή βήμα-βήμα ενός κανονικού επταγώνου με κανόνα και διαβήτη.

Μια ακριβέστερη προσέγγιση

Το κανονικό επτάγωνο με πλευρές $\scriptstyle {S=3{\tfrac {2}{11}}}$ μπορεί να εγγραφεί σε κύκλο διαμέτρου $\scriptstyle {R=3{\tfrac {2}{3}}}$ με σφάλμα μικρότερο του 0,00013%.

Το γεγονός αυτό έπεται από μια ρητή προσέγγιση του $\scriptstyle {{\tfrac {S}{R}}=\ 2\sin {\tfrac {\pi }{7}}\approx 1-({\tfrac {4}{11}})^{2}}$.

Μια απλή κατασκευή κανονικού επταγώνου λ₇ είναι το μήκος της πλευράς κανονικού επταγώνου

Αστεροειδή επτάγωνα

Δύο είδη αστεροειδών επταγώνων μπορούν να κατασκευασθούν από κανονικά επτάγωνα. Είναι τα σχήματα με σύμβολα Schläfli {7/2} και {7/3}.

Μπλε ({7/2}) και πράσινο ({7/3}) αστεροειδή επταγώνα στο εσωτερικό ενός κόκκινου επταγώνου.

Χρήσεις

Σήμερα (2011) το Ηνωμένο Βασίλειο κυκλοφορεί δύο επταγωνικά κέρματα, αυτό των 50 πενών και αυτό των 20 πενών. Το δολάριο των Μπαρμπάντος είναι επίσης επταγωνικό. Το νόμισμα των 20 λεπτών του ευρώ φαίνεται να έχει 7 μικρά βαθουλώματα στην περιφέρειά του. Στην πραγματικότητα, το σχήμα του είναι ένα Επτάγωνο Reuleaux, δηλαδή ένα καμπυλόγραμμο επτάγωνο, οι πλευρές του οποίου κάμπτονται προς τα έξω έτσι ώστε το κέρμα να κυλά ομαλά μέσα σε μηχανήματα αυτόματων πωλητών. Τα κέρματα του Πούλα της Μποτσουάνα των 2 πούλα, 1 πούλα, 50 Thebe και 5 Thebe έχουν επίσης παρόμοιο σχήμα. Κέρματα στο σχήμα επταγώνων Reuleaux κυκλοφορούν στον Μαυρίτιο, στα Ηνωμένα Αραβικά Εμιράτα, στην Τανζανία, στις νήσους Σαμόα, στην Παπούα Νέα Γουινέα, στο Σάο Τομέ και Πρίντσιπε, στην Αϊτή, στη Τζαμάικα, στη Λιβερία, στη Γκάνα, στην Ιορδανία, στο Τζέρσεϊ, στη Νήσο Μαν, στο Γιβραλτάρ, στη Γουιάνα, στις Νήσους Σολομώντα, στις Νήσους Φώκλαντ και στη νήσο της Αγίας Ελένης. Το κέρμα των 1000 Kwacha της Ζάμπια είναι ένα κανονικό επτάγωνο.

Το κέρμα των 25 σεντς της Βραζιλίας έχει ένα επτάγωνο εγγεγραμμένο στον δίσκο του. Μερικές παλιότερες μορφές του θυρεού της Γεωργίας, περιλαμβανόμενης αυτής της σοβιετικής εποχής, έφεραν το επτάγραμμα {7/2}.

Εκτός από το επταγωνικό πρίσμα και το επταγωνικό αντίπρισμα, δεν υπάρχει άλλο πολύεδρο με όλες τις έδρες του κανονικά πολύγωνα που να έχει επταγωνική έδρα.

Τα κανονικά επτάγωνα συναρμόζονται απολύτως, χωρίς κενά μεταξύ τους, ώστε να «πλακοστρώνουν» το υπερβολικό (αλλά όχι το ευκλείδειο) επίπεδο, όπως φαίνεται στην παρακάτω προβολή του προτύπου «δίσκου Poincaré»:

Επταγωνική πλακόστρωση τρίτης τάξεως

Γράφοι

Ο πλήρης γράφος K₇ σχεδιάζεται συχνά ως ένα κανονικό επτάγωνο με τις 21 ακμές του γράφου συνδεδεμένες. Αυτός ο γράφος αναπαριστά επίσης Ορθογραφική προβολή των 7 κορυφών και των 21 ακμών του 6-simplex. Οι 21 και 35 κορυφές του ανορθωμένου και του διανορθωμένου 6-simplex προβάλλονται επίσης ορθογώνια σε κανονικά επτάγωνα.

6-simplex (6D)

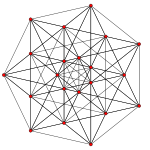Ανορθωμένο 6-simplex (6D)

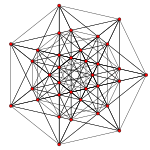Διανορθωμένο 6-simplex (6D)

Επτάγωνες δομές στην φύση

Κ ά κ τ ο ς

Δείτε επίσης

• Επτάγραμμα

Πηγές

1. Σωτήρης Χ. Γκουντουβάς, "Γεωμετρικές Διαδρομές", εκδόσεις Κορφιάτη, Αθήνα 2017

Εξωτερικοί σύνδεσμοι

• Ορισμός και ιδιότητες του επταγώνου με διαδραστική animation
• Μία άλλη μέθοδος προσεγγιστικής κατασκευής
• Πολύγωνα – επτάγωνα
• Πολύ ακριβής προσέγγιση για την κατασκευή κανονικού επταγώνου που ανακαλύφθηκε πρόσφατα.