Δεκατριάγωνο

Στη γεωμετρία, το δεκατριάγωνο ή δεκατρίγωνο (από τις ελληνικές λέξεις δεκατρία και γωνία) είναι ένα οποιοδήποτε πολύγωνο σχήμα με 13 πλευρές και 13 κορυφές. Οι εσωτερικές γωνίες οποιουδήποτε δεκατριαγώνου έχουν άθροισμα 1.980 μοίρες (°), ενώ το σχήμα έχει 65 διαγωνίους.

Κανονικό δεκατριάγωνο

Συνήθως ο όρος δεκατριάγωνο αναφέρεται σε ένα κανονικό δεκατριάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους. Σε ένα τέτοιο δεκατριάγωνο, οι εσωτερικές γωνίες είναι ίσες με 152°18΄ περίπου η καθεμιά. Το σύμβολο Schläfli του κανονικού δεκατριαγώνου είναι {13}.

Το εμβαδό (E) ενός κανονικού δεκατριαγώνου με μήκος πλευράς α δίνεται από τη σχέση:

$E={\frac {13}{4}}a^{2}\cot \left({\frac {\pi }{13}}\right)\simeq 13,1858\,a^{2}.$

Κατασκευή

Επειδή ο 13 είναι μεν πρώτος αριθμός, αλλά όχι πρώτος Φερμά, το κανονικό δεκατριάγωνο δεν είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη. Μπορεί ωστόσο να κατασκευασθεί με νεύση ή με έναν τριχοτομητή γωνίας.

Στο αμέσως επόμενο σχήμα δείχνονται τα στάδια κατασκευής με νεύση ενός κανονικού δεκατριαγώνου με ακτίνα περιγεγραμμένου κύκλου ${\overline {OA}}=12,$ σύμφωνα με τον Άντριου Μ. Γκλήζον, με βάση την τριχοτόμηση γωνίας με μάχαιρα υποδηματοποιού (γαλάζιο).

Κανονικό δεκατριάγωνο με ακτίνα περιγεγραμμένου κύκλου ${\overline {OA}}=12$ σε κλιπ διάρκειας 104 δευτερολέπτων
, με τριχοτόμηση γωνίας με χρήση μάχαιρας υποδηματοποιού (γαλάζιο)

Μια προσεγγιστική κατασκευή κανονικού δεκατριαγώνου με κανόνα και διαβήτη δείχνεται στο παρακάτω σχήμα.

Προσεγγιστική κατασκευή κανονικού δεκατριαγώνου

Μία πιο πολύπλοκη κατασκευή με κανόνα και διαβήτη δίνει ακόμα καλύτερη προσέγγιση:

Προσεγγιστική κατασκευή δεκατριαγώνου σε κλιπ διάρκειας 3,5 λεπτών

Σύμφωνα με το GeoGebra, $\scriptstyle \angle {}$BME₁ = 27,692307692307764° , ενώ 360° ÷ 13 = 27,69230769230769°, δηλαδή η διαφορά είναι λιγότερο από ένα μέρος στα 10 τρισεκατομμύρια.

Συμμετρία

Συμμετρίες ενός κανονικού δεκατριαγώνου. Οι κορυφές είναι χρωματισμένες ανάλογα με τις θέσεις συμμετρίας τους.

Το κανονικό δεκατριάγωνο έχει διεδρική συμμετρία Dih₁₃ , με τάξη 26. Επειδή ο 13 είναι πρώτος αριθμός, υπάρχουν επίσης μία υποομάδα με διεδρική συμμετρία, η Dih₁, και δύο συμμετρίες κυκλικής ομάδας,τις Z₁₃ και Z₁.

Αυτές οι 4 ομάδες συμμετρίας μπορούν να παρατηρηθούν σε 4 διαφορετικές συμμετρίες στο δεκατριάγωνο. Ο Τζων Κόνγουεϊ τις συμβολίζει με ένα γράμμα και την τάξη της ομάδας. Η πλήρης συμμετρία του κανονικού δεκατριαγώνου είναι η r26, ενώ καμιά συμμετρία δεν είναι a1. Οι διεδρικές συμμετρίες διακρίνονται σε αυτές που περνούν από κορυφές (συμβολίζονται με d από τη λέξη diagonal = διαγώνιος), σε αυτές που περνούν από πλευρές (p από τη λέξη perpendiculars = κάθετοι) και σε αυτές των οποίων οι γραμμές ανακλάσεως περνούν από αμφότερες (συμβολίζονται με i).

Η κάθε υποομάδα συμμετρίας επιτρέπει έναν ή περισσότερους βαθμούς ελευθερίας για μη κανονικές μορφές. Μόνο η κυκλική υποομάδα g13 δεν έχει βαθμούς ελευθερίας.

Χρήση ως νόμισμα

Το κανονικό δεκατριάγωνο χρησιμοποιείται ως σχήμα για το κέρμα των 20 κορονών Τσεχίας.

Σχετιζόμενα πολύγωνα

Το αστεροειδές πολύγωνο με δεκατρείς πλευρές ονομάζεται τριδεκάγραμμα. Υπάρχουν 5 κανονικές μορφές του, που συμβολίζονται με τα σύμβολο Schläfli {13/2}, {13/3}, {13/4}, {13/5} και {13/6}.

Τριδεκάγραμμα
Σχήμα	{13/2}	{13/3}	{13/4}	{13/5}	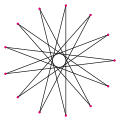{13/6}
Εσωτερική γωνία	≈124,615°	≈96,9231°	≈69,2308°	≈41,5385°	≈13,8462°

Πολύγωνα Petrie

Το κανονικό δεκατριάγωνο είναι το πολύγωνο Πέτρι 12-simplex:

A12
12-simplex