Μαθηματική σταθερά

Οι μαθηματικές σταθερές είναι ιδιαίτεροι αριθμοί, συνήθως πραγματικοί αριθμοί, οι οποίοι έχουν σημαντικό ενδιαφέρον στα μαθηματικά. Οι σταθερές εμφανίζονται σε πολλούς κλάδους των μαθηματικών, με σταθερές όπως ο αριθμός $e$ και το π να εμφανίζονται σε σημαντικά πεδία των μαθηματικών όπως η γεωμετρία, η θεωρία αριθμών και ο λογισμός.

Το πώς καθιερώθηκαν οι σταθερές και γιατί θεωρούνται ενδιαφέρουσες (ή πιο ενδιαφέρουσες από άλλους πραγματικούς αριθμούς), είναι σε ένα βαθμό αντικειμενικό. Κάποιες μαθηματικές σταθερές είναι αξιοσημείωτες κυρίως λόγω ιστορικού ενδιαφέροντος παρά λόγω του μαθηματικού τους ενδιαφέροντος. Οι πιο δημοφιλείς σταθερές μελετήθηκαν εδώ και χιλιάδες χρόνια και έχουν προσεγγιστεί σε πάρα πολλά δεκαδικά ψηφία. Όλες οι μαθηματικές σταθερές είναι αριθμοί οι οποίοι έχουν οριστεί και είναι δυνατό να υπολογιστούν (η σταθερά του Τσάιτιν αποτελεί μια σημαντική εξαίρεση).

Βασικές μαθηματικές σταθερές

Αυτές είναι οι σταθερές που είναι πιο πιθανό να συναντήσει κάποιος κατά τη διάρκεια της φοίτησής του σε σχολεία δευτεροβάθμιας εκπαίδευσης σε πολλές χώρες.

Η Αρχιμήδεια σταθερά π

Η περιφέρεια ενός κύκλου με διάμετρο 1 είναι π.

Η σταθερά π εμφανίζεται φυσικά στην Ευκλείδεια γεωμετρία ως ο λόγος μεταξύ της περιφέρειας και της διαμέτρου ενός κύκλου, αλλά μπορεί να βρεθεί και σε πολλές άλλες περιοχές των μαθηματικών: για παράδειγμα, το ολοκλήρωμα του Γκάους στη μιγαδική ανάλυση, στις μιγαδικές ρίζες της μονάδας στη θεωρία αριθμών και στις κατανομές Κωσύ στη θεωρία πιθανοτήτων. Ωστόσο, η καθολικότητά της δεν περιορίζεται μόνο στα καθαρά μαθηματικά. Διάφοροι τύποι στη φυσική όπως η αρχή της αβεβαιότητας του Χάιζενμπεργκ, και σταθερές όπως η κοσμολογική σταθερά περιλαμβάνουν τη σταθερά π. Η παρουσία του π στις φυσικές αρχές, στους νόμους και στους τύπους μπορεί να έχει πολύ απλές εξηγήσεις. Για παράδειγμα, ο νόμος του Κουλόμπ, περιγράφοντας το μέγεθος της ηλεκτροστατική δύναμη δύο φορτίων ως ανάλογο του γινομένου των μέτρων των δύο φορτίων και αντιστρόφως ανάλογο του τετραγώνου της απόστασης των δύο φορτίων, αναφέρει ότι σε μονάδες SI,

$F={\frac {1}{4\pi \varepsilon _{0}}}{\frac {\left|q_{1}q_{2}\right|}{r^{2}}}$.

Πέρα απ'τη σταθερά ${\varepsilon _{0}}$ που αντιστοιχεί στην διηλεκτρική σταθερά στο κενό, ο όρος ${4\pi r^{2}}$ στον παρονομαστή εκφράζει την επιφάνεια μιας σφαίρας με ακτίνα $r$, έχοντας έτσι μια πολύ συγκεκριμένη έννοια. Η αριθμητική τιμή του π είναι περίπου 3,14159. Πολλοί άνθρωποι διαγωνίζονται στο ποιος θα απομνημονεύσει περισσότερα ψηφία του π.

Η εκθετική συνάρτηση (πράσινη γραμμή) περιγράφει πολλά φυσικά φαινόμενα.

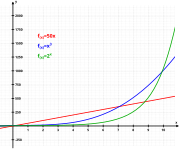
Αριθμός e του Όιλερ

Ο αριθμός του Όιλερ e (γνωστός και ως σταθερά του Νέιπιερ), εμφανίζεται σε πολλούς κλάδους των μαθηματικών και μπορεί να οριστεί ως η τιμή του ακόλουθου ορίου:

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$.

Για παράδειγμα, ο Ελβετός μαθηματικός Γιακόμπ Μπερνούλι ανακάλυψε ότι το $e$ εμφανίζεται στους τόκους: ένας λογαριασμός που ξεκινά από 1€ με ετήσιο επιτόκιο R και με συνεχή ανατοκισμό, θα αυξηθεί κατά e^R δολλάρια στο τέλος του ενός έτους. Ο υπολογισμός έχει ως εξής: Αν χωρίσουμε τον χρόνο με $n$ ίσα τμήματα και σε κάθε ένα υπάρχει ανατοκισμός $R/n$, τότε το τελικό ποσό μετά από έναν χρόνο είναι ίσο με

$S_{n}=\left(1+{\frac {R}{n}}\right)^{n}.$

Επειδή είμαστε στον συνεχή ανατοκισμό παίρνουμε το όριο του $n\to \infty$, δηλαδή

${\begin{aligned}\lim _{n\to \infty }S_{n}&=\lim _{n\to \infty }\left(\left(1+{\frac {R}{n}}\right)^{n/R}\right)^{R}\\&=\left(\lim _{n\to \infty }\left(1+{\frac {R}{n}}\right)^{n/R}\right)^{R}\\&=\left(\lim _{n/R\to \infty }\left(1+{\frac {R}{n}}\right)^{n/R}\right)^{R}\\&=e^{R}.\end{aligned}}$

Η σταθερά $e$ έχει επίσης εφαρμογές στην θεωρία πιθανοτήτων όπου εμφανίζεται με έναν τρόπο ο οποίος φαίνεται να μην σχετίζεται με την εκθετική αύξηση. Ας υποθέσουμε ότι ένας παίκτης παίζει έναν κουλοχέρη με $1/n$ πιθανότητα να κερδίσει, και παίζει $n$ φορές.. Στη συνέχεια, για μεγάλα n  (όπως ένα εκατομμύριο), η πιθανότητα ο παίκτης να μην κερδίσει ποτέ είναι περίπου 1/e και η πιθανότητα τείνει σε αυτήν την τιμή όταν το n τείνει στο άπειρο. Η πιθανότητα να μην κερδίσει ένα παιχνίδι είναι

$p=1-{\frac {1}{n}}$.

Επειδή τα παιχνίδια είναι ανεξάρτητα η πιθανότητα να μην κερδίσει κανένα παιχνίδι είναι

$p^{n}=\left(1-{\frac {1}{n}}\right)^{n}$.

Παίρνοντας το όριο για $n\to \infty$, έχουμε ότι

$\lim _{n\to \infty }\left(1-{\frac {1}{n}}\right)^{n}=e^{-1}={\frac {1}{e}}$.

Έχουμε ότι $1/e=0.3678...$ και για $n=4$ λαμβάνουμε $0.316...$, για $n=5$ λαμβάνουμε $0.327...$ και για $n=100$ λαμβάνουμε $0.366...$.

Μια άλλη εφαρμογή του e, που ανακαλύφθηκε εν μέρει από τον Γιακόμπ Μπερνούλι μαζί με τον Γάλλο  μαθηματικό Pierre Raymond de Montmort είναι το πρόβλημα διασάλευσης. Εδώ $n$ επισκέπτες καλούνται σε ένα πάρτι και στην πόρτα κάθε επισκέπτης δίνει το καπέλο του στον μπάτλερ ο οποίος τα τοποθετεί σε επίσημα κουτιά. Ο μπάτλερ δε γνωρίζει τα ονόματα των καλεσμένων και έτσι βάζει τα καπέλα τυχαία στα κουτιά. Στο τέλος του πάρτι δίνει τυχαία ένα κουτί σε κάθε καλεσμένο. Το πρόβλημα του de Montmort είναι: ποια είναι η πιθανότητα κανένα καπέλα να μην επιστραφεί στον σωστό αποδέκτη. Η απάντηση είναι:

$p_{n}=1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+\cdots +(-1)^{n}{\frac {1}{n!}},$

και καθώς το $n$ τείνει στο άπειρο, το $p_{n}$ προσεγγίζει το $1/e$. Το $e$ εμφανίζεται και σε πολλά άλλα μέρη των πιθανοτήτων, συμπεριλαμβανομένων του προβλήματος της γραμματέως και στην αναμενόμενη τιμή του μήκους μίας μονότονης ακολουθίας σε μία τυχαία μετάθεση.

Ο αριθμός e είναι άρρητος και η αριθμητική του τιμή είναι περίπου $2,7182818284$  A001113.

Η Πυθαγόρεια σταθερά √2

Η τετραγωνική ρίζα του 2 είναι ίση με το μήκος της υποτείνουσας ενός ορθογωνίου τριγώνου με κάθετες πλευρές μήκους 1.

Η τετραγωνική ρίζα του 2, συχνά γνωστή και ως ρίζα 2, ριζικό του 2 ή σταθερά του Πυθαγόρα, γράφεται ως √2 και είναι ο θετικός πραγματικός αριθμός ο οποίος πολλαπλασιάζοντάς τον με τον εαυτό του δίνει τον αριθμό $2$. Ονομάζεται ακριβέστερα κύρια τετραγωνική ρίζα του 2, για να διακρίνεται ο αριθμός αυτός απ'τον αρνητικό αριθμό με την ίδια ιδιότητα, δηλαδή τον $-{\sqrt {2}}$.

Γεωμετρικά η τετραγωνική ρίζα του 2 είναι το μήκος της διαγωνίου σε ένα τετράγωνο με πλευρές μήκους ένα. Αυτό προκύπτει από το πυθαγόρειο θεώρημα. Ήταν ίσως ο πρώτος γνωστός άρρητος. Η αριθμητική του τιμή σε προσέγγιση 65 δεκαδικών ψηφίων είναι:

1.41421356237309504880168872420969807856967187537694807317667973799...  A002193.

Η τετραγωνική ρίζα του 2 στον άξονα των πραγματικών αριθμών.

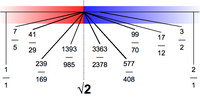
Συχνά χρησιμοποιείται η προσέγγιση $99/70$ ($\approx 1.41429/$) για την τετραγωνική ρίζα του δύο. Παρά το γεγονός ότι έχει σχετικά μικρό παρανομαστή, μόλις $70$ η προσέγγιση διαφέρει από την κανονική τιμή λιγότερο από $1/10,000$ (περίπου $7,2\cdot 10^{-5}$).

Η φανταστική μονάδα i

Το i στο μιγαδικό ή καρτεσιανό επίπεδο. Οι πραγματικοί αριθμοί βρίσκονται στον οριζόντιο άξονα και οι φανταστικοί στον κατακόρυφο.

Η φανταστική μονάδα ή αλλιώς φανταστικός αριθμός, συμβολίζεται ως $i$, είναι μια μαθηματική έννοια που επεκτείνει το πραγματικό αριθμητικό σύστημα ℝ  στο μιγαδικό αριθμητικό σύστημα $\mathbb {C}$ στο οποίο κάθε πολυώνυμο $P(x)$ έχει μία τουλάχιστον ρίζα (βλέπε αλγεβρική κλειστότητα  και θεμελιώδες θεώρημα της άλγεβρας). Η βασική σχέση που ικανοποιεί η φανταστική μονάδα είναι $i^{2}=-1$. Ο όρος "φανταστικός" χρησιμοποιείται επειδή δεν υπάρχει πραγματικός αριθμός ο οποίος έχει αρνητικό τετράγωνο.

Υπάρχουν δύο μιγαδικές τετραγωνικές ρίζες του $-1$, δηλαδή το $i$ και το $-i$, όπως υπάρχουν δύο μιγαδικές τετραγωνικές ρίζες για κάθε άλλο πραγματικό αριθμό εκτός από το μηδέν που έχει μία διπλή τετραγωνική ρίζα.

Στις περιπτώσεις όπου το $i$ είναι αμφίσημο ή προβληματικό, το j ή το ελληνικό ι (βλέπε εναλλακτικούς συμβολισμούς) χρησιμοποιούνται συνήθως. Στους κλάδους της ηλεκτρολογίας και των συστημάτων μηχανικού ελέγχου, η φανταστική μονάδα συχνά συμβολίζεται με $J$ αντί του $i$, γιατί το $i$ συνήθως χρησιμοποιείται για να υποδηλώσει το ηλεκτρικό ρεύμα σε αυτούς τους κλάδους.

Σταθερές στα ανώτερα μαθηματικά

Παρακάτω δίνονται σταθερές που εμφανίζονται συχνά στα ανώτερα μαθηματικά.

Οι σταθερές του Feigenbaum α και δ

διάγραμμα διακλάδωσης της λογιστικής απεικόνισης.

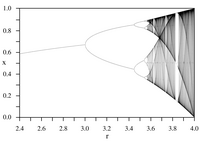
Οι επαναλήψεις των συνεχών απεικονίσεων θεωρούνται από τα πιο απλά παραδείγματα μοντέλων για δυναμικά συστήματα. Οι δύο σταθερές ονομάστηκαν έτσι εξαιτίας του φυσικομαθηματικού Mitchell Feigenbaum και εμφανίζονται στις εξής επαναληπτικές διαδικασίες: ως μαθηματικές σταθερές των λογιστικών απεικονίσεων με τετραγωνικά μέγιστα σημεία και τα διαγράμματα διακλάδωσής τους.

Η λογιστική απεικόνιση είναι ένα πολυώνυμο χαρτογράφησης, συχνά δίνεται ως ένα αρχετυπικό παράδειγμα των τρόπων με τους οποίους εξηγεί πως η χαοτική συμπεριφορά μπορεί να προκύψει από πολύ απλές μη-γραμμικές δυναμικές εξισώσεις. Η απεικόνιση δημοσιεύθηκε σε μια εργασία το 1976 από τον Αυστραλιανό βιολόγο Robert May, εν μέρει, ως ένα διακριτού-χρόνου δημογραφικό ανάλογο στη λογιστική εξίσωση που για πρώτη φορά δημιουργήθηκε από τον Pierre François Verhulst. Η διαφορική εξίσωση  προορίζεται για να συλλάβει τις δύο επιδράσεις της αναπαραγωγής και της λιμοκτονίας.

Η αριθμητική τιμή της α είναι περίπου $2.5029$ ( A006891). Η αριθμητική τιμή της δ είναι προσεγγιστικά $4.6692$ ( A006890).

Η σταθερά του Apéry ζ(3)

Η σταθερά του Apéry ορίζεται ως η τιμή του αθροίσματος της παρακάτω σειράς

$\zeta (3)=1+{\frac {1}{2^{3}}}+{\frac {1}{3^{3}}}+{\frac {1}{4^{3}}}+\cdots$.

Η σταθερά αυτή είναι ένας άρρητος αριθμός και η τιμή της είναι περίπου $1.2020569$ ( A002117).

Παρά την ειδική σημασία της στην συνάρτηση ζήτα του Ρίμαν, η σταθερά του Apéry εμφανίζεται σε πλήθος φυσικών προβλημάτων, συμπεριλαμβανομένων των δεύτερης και τρίτης τάξης όρων της γυρομαγνητικής αναλογίας του ηλεκτρονίου, που υπολογίζεται με τη χρήση της κβαντικής ηλεκτροδυναμικής.

Η χρυσή τομή φ 

Τα χρυσά παραλληλόγραμμα σε ένα εικοσάεδρο.

$F\left(n\right)={\frac {\varphi ^{n}-(1-\varphi )^{n}}{\sqrt {5}}}$

Ένας αυστηρός τύπος για το $n$-οστό όρο της ακολουθίας Φιμπονάτσι συναρτήσει του φ.

Ο αριθμός φ, επίσης αποκαλείται χρυσή τομή, χρησιμοποιείται συχνά στη γεωμετρία, ιδιαίτερα σε σχήματα με πενταγωνική συμμετρία. Πράγματι, το μήκος της διαγωνίου ενός κανονικού πενταγώνου είναι $\varphi$ φορές την πλευρά του. Οι κορυφές ενός κανονικού εικοσαέδρου είναι εκείνες των τριών αμοιβαία καθέτων χρυσών ορθογωνίων. Επίσης, εμφανίζεται στην ακολουθία Φιμπονάτσι, και καθορίζει την εκθετική της αύξηση. Η χρυσή τομή έχει την πιο αργή σύγκλιση από οποιοδήποτε άρρητο αριθμό. Είναι, για αυτόν τον λόγο, μία από τις χειρότερες περιπτώσεις του θεωρήματος προσέγγισης του Λαγκράνζ και μια ακραία περίπτωση της ανισότητας του Hurwitz για τις διοφαντικές προσεγγίσεις. Αυτή ίσως μπορεί να είναι η εξήγηση γιατί οι γωνίες που βρίσκονται κοντά στη χρυσή αναλογία συχνά απεικονίζονται στην phyllotaxis (ανάπτυξη των φυτών). Ο αριθμός $\varphi ={\tfrac {1+{\sqrt {5}}}{2}}$ και προσεγγιστικά είναι ίσος με $1,61803398874$ ( A001622).

Η σταθερά γ των Όιλερ-Mascheroni

Η σταθερά Όιλερ-Mascheroni είναι μια σταθερά που ορίζεται ως το εξής όριο:

$\gamma =\lim _{n\to \infty }\left(\left(\sum _{i=1}^{n}{\frac {1}{i}}\right)-\ln n\right)$.

Η σταθερά των Όιλερ-Mascheroni εμφανίζεται, στο τρίτο θεώρημα του Merten και έχει σχέση με την συνάρτηση γάμμα, τη συνάρτηση ζήτα και πολλά άλλα ολοκληρώματα και σειρές. Ο ορισμός της σταθεράς των Euler-Mascheroni παρουσιάζει στενή σχέση μεταξύ των διακριτών και των συνεχών μαθηματικών. Η αριθμητική τιμή της $\gamma$ είναι περίπου $0,57721$ ( A001620).

Η σταθερά λ του Κόνγουεϊ

${\begin{matrix}1\\11\\21\\1211\\111221\\312211\\\vdots \end{matrix}}$

η ακολουθία look-and-say του Κόνγουεϊ

Η σταθερά του Κόνγουεϊ είναι ο αναλλοίωτος ρυθμός αύξησης όλων των συμβολοσειρών που προέρχονται παρόμοια με την ακολουθία look-and-say  (με εξαίρεση μερικές τετριμμένες), και συνήθως συμβολίζεται ως $\lambda$.

Δίνεται από τη μοναδική θετική πραγματική ρίζα ενός πολυωνύμου 71^ου βαθμού  με ακέραιους συντελεστές. Η τιμή του $\lambda$ είναι περίπου $1,30357$ ( A014715).

Η σταθερά K του Khinchin

Εάν ένας πραγματικός αριθμός $r$ είναι γραμμένος ως ένα απλό συνεχές  κλάσμα:

$r=a_{0}+{\dfrac {1}{a_{1}+{\dfrac {1}{a_{2}+{\dfrac {1}{a_{3}+\cdots }}}}}}$,

όπου $a_{k}$ είναι φυσικοί αριθμοί για όλα τα $k$, τότε, σύμφωνα με το Ρώσο μαθηματικό  Aleksandr Khinchin, ο οποίος  απέδειξε το 1934, ότι το όριο του γεωμετρικού μέσου $(a_{1}a_{2}\cdot \ldots \cdot a_{n})^{1/n}$ όσο το $n$ τείνει προς το άπειρο, υπάρχει και μάλιστα είναι μια σταθερά, η σταθερά Κ του Khinchin, (σε όλα τα συνεχή κλάσματα εκτός από ένα σύνολο μέτρου 0).

Η αριθμητική τιμή του $K$ είναι περίπου $2,6854520010$ ( A002210).

Η σταθερά A των Glaisher-Kinkelin

Η σταθερά Α των Glaisher-Kinkelin ορίζεται ως το όριο:

$A=\lim _{n\rightarrow \infty }{\frac {\prod _{k=1}^{n}k^{k}}{n^{n^{2}/2+n/2+1/12}e^{-n^{2}/4}}}$.

Πρόκειται για μία σημαντική σταθερά η οποία εμφανίζεται σε πολλούς τύπους για την παράγωγο της συνάρτησης ζήτα του Ρίμαν. Η τιμή της Α είναι περίπου $1,2824271291$ ( A074962).

Μαθηματικές ανησυχίες και απροσδιόριστες σταθερές

Απλοί εκπρόσωποι συνόλων αριθμών

Μερικές σταθερές, όπως η τετραγωνική ρίζα του 2, η σταθερά Λιουβίλ και η σταθερά Champernowne

$C_{10}=0.{\color {blue}{1}}2{\color {blue}{3}}4{\color {blue}{5}}6{\color {blue}{7}}8{\color {blue}{9}}10{\color {blue}{11}}12{\color {blue}{13}}14{\color {blue}{15}}16\dots$

δεν είναι σημαντικές μαθηματικές σταθερές αλλά εξακολουθούν να έχουν ενδιαφέρον γιατί αποτελούν απλούς εκπροσώπους ειδικών συνόλων αριθμών όπως των άρρητων , των υπερβατικών και των κανονικών αριθμών (με βάση το 10) αντίστοιχα. Η ανακάλυψη των άρρητων αριθμών αποδίδεται συνήθως στον Πυθαγόρειο φιλόσοφο Ίππασο τον «Μεταπόντιο» ο οποίος απέδειξε, κατά πάσα πιθανότητα με γεωμετρικό τρόπο, ότι η τετραγωνική ρίζα του 2 είναι άρρητος αριθμός. Όσον αφορά τη σταθερά του Λιουβίλ,η οποία πήρε το όνομα της από το Γάλλο μαθηματικό Ζοζέφ Λιουβίλ, ήταν ο πρώτος αριθμός που αποδείχθηκε ότι ήταν υπερβατικός.

Σταθερά Ω του Τσάιτιν

Στην θεωρητική πληροφορική και την θεωρία πληροφορίας, η σταθερά του Τσάιτιν είναι ο πραγματικός αριθμός που αντιπροσωπεύει την πιθανότητα με την οποία μια τυχαία επιλεγμένη Μηχανή Τούρινγκ θα τερματήσει. Η σταθερά του Τσάιτιν δημιουργηθηκε από τον Αργεντινο-Αμερικανό μαθηματικό και επιστήμονα ηλεκτρονικών υπολογιστών Γκρέγκορυ Τσάιτιν.Η σταθερα αυτή, αν και δε μπορεί να υπολογιστεί με ακρίβεια, έχει αποδειχθεί πως είναι υπερβατικός και κανονικός αριθμός. Η σταθερά δεν είναι καθολική, αφού εξαρτάται σημαντικά από την εκάστοτε αριθμιτική κωδικοποίηση που χρησιμοποιείται για τις μηχανές Τιούρινγκ, ωστόσο οι ενδιαφέρουσες ιδιότητες της είναι ανεξάρτητες της κωδικοποίησης που χρησιμοποιείται.

Απροσδιόριστες σταθερές

Όταν δεν προσδιορίζονται, οι σταθερές υποδηλώνουν κλάσεις παρόμοιων αντικειμένων, συνήθως συναρτήσεων, οι οποίες αντιπροσοπεύονται από μία σταθερά. Τέτοιες σταθερές συναντώνται συχνά όταν ασχολούμαστε με ολοκληρώματα και διαφορικές εξισώσεις. Παρ' όλο που δεν προσδιόριζονται, εχουν συγκεκριμένη τιμή, η οποία πολλές φορές δεν παίζει σημαντικό ρόλο στη λυση του προβλήματος.

Στα ολοκληρώματα

Τα αόριστα ολοκληρώματα ονομάζονται έτσι διότι οι λύσεις τους διαφέρουν μόνο σε μια σταθερά. Για παράδειγμα, όταν δουλεύουμε στους πραγματικούς αριθμούς, έχουμε ότι

$\int \cos x\ dx=\sin x+C$

όπου $C$, η σταθερά ολοκλήρωσης, είναι ένας αυθαίρετος σταθερός πραγματικός αριθμός. Με άλλα λόγια, οποιαδήποτε κι αν είναι η τιμή της σταθεράς $C$ ,η παράγωγος του $\sin x+C$ ως προς $x$ πάντοτε δίνει $\cos x$.

Στις διαφορικές εξισώσεις

Με παρόμοιο τρόπο, σταθερές εμφανίζονται στις λύσεις διαφορικών εξισώσεων στις οποίες δεν δίνονται αρκετές αρχικές τιμές ή συνθήκες περιορισμών. Για παράδειγμα, η συνήθης διαφορική εξίσωση

${\tfrac {df}{dx}}=f(x)$,

έχει λύση την $f(x)=Ce^{x}$ όπου το $C$ είναι αυθαίρετη σταθερά.

Όταν ασχολούμαστε με μερικές διαφορικές εξισώσεις, οι σταθερές ίσως είναι συναρτήσεις, δηλαδή μπορεί να είναι συναρτήσεις ως προς μεταβλητές οι οποίες δεν είναι μεταβλητές παραγώγισης. Για παράδειγμα, η μερική διαφορική εξίσωση

${\frac {\partial f(x,y)}{\partial x}}=0$,

έχει λύσεις $f(x,y)=C(y)$, όπου $C(y)$ είναι αυθαίρετη συνάρτηση της μεταβλητής $y$.

Συμβολισμός

Αναπαράσταση σταθερών

Είναι συνηθισμένο να εκφράζουμε την αριθμητική τιμή μιας σταθεράς χρησιμοποιώντας τη δεκαδική της αναπαράσταση (ή τουλάχιστον κάποια από τα πρώτα ψηφία της αναπαράστασης). Αυτή η αναπαράσταση όμως ίσως προκαλέσει προβλήματα για δύο λόγους. Πρώτον, παρ' όλο που όλοι οι ρητοί έχουν πεπερασμένο ή συνεχώς επαναλαμβανόμενο δεκαδικό ανάπτυγμα, οι άρρητοι ωστόσο δεν έχουν τέτοιου είδους έκφραση κι αυτό τους καθιστά αδύνατο να περιγραφούν εντελώς με τέτοιο τρόπο. Επίσης, το δεκαδικό ανάπτυγμα ενός αριθμού δεν είναι απαραίτητα μοναδικό. Για παράδειγμα, οι δύο αναπραστάσεις 0.999 και 1 είναι ισοδύναμες με την έννοια ότι αντιπροσωπεύουν τον ίδιο αριθμό.

Ο υπολογισμός του δεκαδικού αναπτύγματος των σταθερών έχει αποτελέσει συνηθισμένο εγχείρημα ανά τους αιώνες. Για παράδειγμα ο Γερμανός μαθηματικός Ludolph van Ceulen που έζησε το 16ο αιώνα αφιέρωσε σημαντικό κομμάτι της ζωής του στον υπολογισμό των πρώτων 35 ψηφίων του ππ. Χρησιμοποιώντας υπολογιστές και υπερ-υπολογιστές έχουν υπολογιστεί περισσότερα από εκατό δισεκατομμύρια ψηφία κάποιων μαθηματικών σταθερών συμπεριλαμβανομένων του π, του $e$ και της τετραγωνικής ρίζας του 2. Έχουν αναπτυχθεί γρήγοροι αλγόριθμοι, κάποιοι από τους οποίους - όπως αυτός για τη σταθερά του Apéry- είναι απροσδόκητα γρήγοροι.

$G=\left.{\begin{matrix}3\underbrace {\uparrow \ldots \uparrow } 3\\\underbrace {\vdots } \\3\uparrow \uparrow \uparrow \uparrow 3\end{matrix}}\right\}{\text{64 layers}}$

Ο αριθμός Graham ορίζεται χρησιμοποιώντας τον συμβολισμό του Κνουθ με άνω βέλος.

Κάποιες σταθερές διαφέρουν τόσο πολύ από το συνηθισμένο είδος ώστε έχει εφευρεθεί ένας νέος συμβολισμός για να τις αναπαριστούμε ικανοποιητικά. Κάτι τέτοιο απεικονίζεται στη διπλανή εικόνα στον αριθμό του Graham, όπου χρησιμοποιείται ο συμβολισμός του Κνουθ με άνω βέλος.

Πολλές φορές τις αναπαριστάμε χρησιμοποιώντας συνεχή κλάσματα όταν διεξάγουμε διάφορες έρευνες, όπως στατιστικές αναλύσεις. Πολλές μαθηματικές σταθερές έχουν μια αναλυτική μορφή, αυτό σημαίνει ότι μπορούν να κατασκευαστούν χρησιμοποιώντας ευρέως γνώστες πράξεις που μπορούν να χρησιμοποιηθούν και για τον υπολογισμό τους. Δεν έχουν όλες οι σταθερές αναλυτικές μορφές όπως συμβαίνει για παράδειγμα με τη σταθερά Grossman και τη σταθερά Foias.

Συμβολισμός και ονομασία των σταθερών

Η χρήση γραμμάτων για το συμβολισμό των σταθερών είναι ένας τρόπος που χρησιμοποιείται συχνά για να κάνουμε το συμβολισμό πιο συνοπτικό. Μια καθιερωμένη σύμβαση, η οποία ξεκίνησε από τον Λέοναρντ Όιλερ το 18ο αιώνα,είναι η χρήση πεζών γραμμάτων από την αρχή του λατινικού αλφαβήτου, δηλαδή $a,b,c,\ldots$ ή του ελληνικού αλφαβήτου $\alpha ,\beta ,\gamma ,\ldots$ για την ονομασία των σταθερών.

Ωστόσο, για κάποιες πιο σημαντικές σταθερές, τα σύμβολα μπορεί να είναι πιο περίπλοκα και να έχουν κάποιο επιπλέον γράμμα, αστερίσκο, αριθμό, λημνίσκο ή χρήση γραμμάτων από άλλα αλφάβητα όπως το εβραϊκό,το κυριλικικό ή το γοτθικό.

$\mathrm {googol} =10^{100}\,\ ,\ \mathrm {googolplex} =10^{\mathrm {googol} }=10^{10^{100}}\,$

Μερικές φορές το σύμβολο που αναπαριστά μια σταθερά είναι μια ολόκληρη λέξη. Για παράδειγμα, ο 9χρονος ανιψιός του αμερικανού μαθηματικού Edward Kasner επινόησε τα ονόματα googol και googolplex.

Γενικότερα, τα ονόματα των σταθερών συνδέονται είτε με τη σημασία της σταθεράς (καθολική παραβολική σταθερά, σταθερά των δίδυμων πρώτων αριθμών, ..) είτε με κάποιο συγκεκριμένο πρόσωπο (σταθερά Sierpiński, σταθερά Josephson, ..).

Δείτε επίσης

• π (μαθηματική σταθερά)
• e (μαθηματική σταθερά)
• Χρυσή τομή
• Τετραγωνική ρίζα του 2
• Τετραγωνική ρίζα του 3
• Τετραγωνική ρίζα του 5