Πυθαγόρειο θεώρημα

Στην Ευκλείδεια γεωμετρία, το Πυθαγόρειο θεώρημα (ή θεώρημα του Πυθαγόρα) είναι το θεώρημα που συσχετίζει τα τετράγωνα των πλευρών ενός ορθογωνίου τριγώνου. Πιο συγκεκριμένα, σε ένα ορθογώνιο τρίγωνο με την ορθή, ισχύει ότι
- ,
όπου και τα μήκη των δύο κάθετων πλευρών και το μήκος της υποτείνουσας.
O Ευκλείδης στο πρώτο βιβλίο των Στοιχείων Γεωμετρίας του (47η πρόταση) δίνει την εξής διατύπωση[1]:
- «ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις.».
Δηλαδή:
- «το τετράγωνο της υποτείνουσας ενός ορθογώνιου τριγώνου ισούται με το άθροισμα των τετραγώνων των δύο καθέτων πλευρών».
Στο ίδιο βιβλίο, ο Ευκλείδης παραθέτει τη σχετική απόδειξη που κατά παράδοση οφείλεται στον Πυθαγόρα, ο οποίος κατ' άλλη, επίσης αρχαία, παράδοση, μετά την ανακάλυψή του αυτή θυσίασε προς τους θεούς εκατόμβη, γι' αυτό και το θεώρημα αυτό ονομάσθηκε «Εκατόμβη» ή «Θεώρημα εκατόμβης».
Αν και το θεώρημα σήμερα φέρει το όνομα του Έλληνα μαθηματικού Πυθαγόρα (570 π.Χ.- 495 π.Χ.), από ιστορικές έρευνες φαίνεται ότι είχε διατυπωθεί και νωρίτερα (ως εμπειρική παρατήρηση). Υπάρχουν αποδείξεις ότι Βαβυλώνιοι μαθηματικοί είχαν κατανοήσει τον τρόπο λειτουργίας του θεωρήματος, αν και δεν υπάρχει σχεδόν καμία απόδειξη ότι το χρησιμοποίησαν σε μαθηματικά πλαίσια. Μαθηματικοί από τη Μεσοποταμία, την Ινδία και την Κίνα είναι επίσης γνωστοί για το ότι είχαν ανακαλύψει το αποτέλεσμα του θεωρήματος αποδεικνύοντας το επιπλέον, σε συγκεκριμένες περιπτώσεις.
Το θεώρημα έχει μεγάλο αριθμό αποδείξεων, πιθανότατα μεγαλύτερο από κάθε άλλο μαθηματικό θεώρημα. Οι αποδείξεις είναι ευθείες και το σύνολο τους συμπεριλαμβάνει τόσο γεωμετρικές όσο και αλγεβρικές αποδείξεις, κάποιες από της οποίες χρονολογούνται αρκετές χιλιετίες πριν. Το θεώρημα μπορεί να γενικευτεί με πολλούς τρόπους, σε χώρους μεγαλύτερης διάστασης, σε μη ευκλείδειους χώρους, σε μη ορθογώνια τρίγωνα ή ακόμα και σε ν-διάστατα στερεά.
Ισχύει και το αντίστροφο Πυθαγόρειο Θεώρημα: ότι δηλαδή, αν ισχύει η παραπάνω σχέση μεταξύ των πλευρών ενός τριγώνου, τότε το τρίγωνο είναι ορθογώνιο.
Ιστορικά[Επεξεργασία | επεξεργασία κώδικα]

Υπάρχει μία διαφωνία για το κατά πόσο το πυθαγόρειο θεώρημα ανακαλύφθηκε μία φορά ή πολλές φορές σε διαφορετικά μέρη.
Η ιστορία του πυθαγορείου θεωρήματος μπορεί να διαιρεθεί σε τέσσερα μέρη: ανακάλυψη των πυθαγόρειων τριάδων, ανακάλυψη της σχέσης μεταξύ των πλευρών ενός ορθογωνίου τριγώνου, ανακάλυψη των σχέσεων μεταξύ ομοίων τριγώνων και αποδείξεις του θεωρήματος στα πλαίσια κάποιου επαγωγικού συστήματος.
Ο Bartel Leendert van der Waerden (1903–1996) υπέθεσε ότι πυθαγόρειες τριάδες ανακαλύφθηκαν αλγεβρικά από τους Βαβυλώνιους. Γραμμένος μεταξύ του 200 και του 1786 π.Χ., την περίοδο του Μέσου Βασιλείου της Αιγύπτου, ο αιγυπτιακός πάπυρος του Βερολίνου 6619 συμπεριλαμβάνει ένα πρόβλημα του οποίου η λύση είναι η πυθαγόρεια τριάδα 6,8,10, στο οποίο όμως δεν γίνεται αναφορά σε ορθογώνιο τρίγωνο. Ο πίνακας Plimpton 322, γραμμένος στη Μεσοποταμία μεταξύ του 1790 και του 1750 π.Χ. κατά τη διάρκεια της βασιλείας του Χαμουραμπί, περιέχει πολλές αναφορές σχετικές με πυθαγόρειες τριάδες. Από αιγυπτιακά μεγαλιθικά μνημεία των οποίων οι πλευρές είναι ακέραια πολλαπλάσια, φαίνεται ότι οι ιδιότητες των ορθογωνίων τριγώνων και οι σχέσεις των πλευρών τους, ήταν γνωστές από πολύ παλιά.
Στην Ινδία, το βιβλίο Baudhayana Sulba Sutra (οδηγίες για κατασκευή ναών), το οποίο χρονολογείται μεταξύ του 8ου και του 2ου αιώνα π.Χ., περιέχει μία λίστα από πυθαγόρειες τριάδες που ανακαλύφθηκαν αλγεβρικά, μία διατύπωση του πυθαγορείου θεωρήματος και μία γεωμετρική απόδειξη του θεωρήματος για ένα ισοσκελές ορθογώνιο τρίγωνο (Το σχοινί που εκτείνεται κατά μήκος της διαγωνίου ενός ορθογωνίου, παράγει επιφάνεια ίδια με αυτή της κάθετης και της οριζόντιας πλευράς). Το Apastamba Sulba Sutra (600 π.Χ.) περιέχει μία γενική αριθμητική απόδειξη του θεωρήματος, χρησιμοποιώντας τον υπολογισμό ενός εμβαδού. Ο Van der Waerden πίστευε ότι σίγουρα βασιζόταν σε παλαιότερες παραδόσεις. Ο Boyer (1991) υποστηρίζει ότι στοιχεία που βρέθηκαν στο Sulba Sutra προέρχονται από λαούς της Μεσοποταμίας.
Με περιεχόμενο γνωστό πολύ νωρίτερα αλλά διασωθέν σε κείμενα που χρονολογούνται τον 1ο αιώνα π.Χ., το κινέζικο κείμενο Zhou Bi Suan Jing δίνει μία αιτιολόγηση του πυθαγορείου θεωρήματος για την τριάδα 3,4,5- στην Ινδία είναι γνωστό και ως "θεώρημα Gougu". Κατά τη διάρκεια της δυναστείας Χαν (202 π.Χ.-220 μ.Χ.), οι πυθαγόρειες τριάδες εμφανίζονται στο "Εννέα κεφάλαια της μαθηματικής τέχνης" μαζί με μία αναφορά σε ορθογώνια τρίγωνα. Πολλοί πιστεύουν ότι το θεώρημα πρώτα ανακαλύφθηκε στην Κίνα, όπου ονομάζεται και Θεώρημα Shang Gao, από το όνομα του αστρονόμου και μαθηματικού δούκα του Zhou, του οποίου το έργο συνιστά το μεγαλύτερο μέρος του Zhou Bi Suan Jing.
Ο Πυθαγόρας χρησιμοποίησε αλγεβρικές μεθόδους για να κατασκευάσει πυθαγόρειες τριάδες, σύμφωνα με το σχολιασμό του Πρόκλου στον Ευκλείδη. Ο Πρόκλος όμως, έγραψε μεταξύ του 410 και 485 μ.Χ. Σύμφωνα με τον Thomas L. Heath (1861–1940), δεν επιβιώνει καμία συγκεκριμένη απόδοση του θεωρήματος στον Πυθαγόρα στην ελληνική λογοτεχνία τους 5 αιώνες αφότου εκείνος έζησε. Παρ'όλα αυτά, όταν συγγραφείς όπως ο Ευκλείδης και Κικέρων, το έκαναν με τρόπο που υποδήλωνε ότι το γεγονός ήταν ευρέως γνωστό και αναμφισβήτητο. Είτε το η ανακάλυψη του θεωρήματος αποδίδεται προσωπικά στον Πυθαγόρα είτε όχι, το σίγουρο είναι ότι σε κάθε περίπτωση, η ανακάλυψη του θεωρήματος χρονολογείται την εποχή των πυθαγόρειων μαθηματικών.
Γύρω στο 400 π.Χ., σύμφωνα με τον Πρόκλο, ο Πλάτωνας έδωσε μία μέθοδο για την εύρεση πυθαγόρειων τριάδων που συνδυάζει άλγεβρα και γεωμετρία. Γύρω στα 300 π.Χ., στα Στοιχεία του Ευκλείδη παρουσιάζεται η πρώτη εκτενής αξιωματική απόδειξη του θεωρήματος.
Πυθαγόρεια απόδειξη[Επεξεργασία | επεξεργασία κώδικα]

Το πυθαγόρειο θεώρημα ήταν γνωστό πολύ πριν τον Πυθαγόρα, αλλά φαίνεται να είναι αυτός ο πρώτος που κατάφερε να το αποδείξει. Σε κάθε περίπτωση, η απόδειξη που του αποδίδεται είναι πολύ απλή και ονομάζεται απόδειξη με ανακατανομή.
Καθένα από τα δύο μεγάλα τετράγωνα της εικόνας περιέχει τέσσερα όμοια τρίγωνα και η μόνη διαφορά τους είναι ότι τα τρίγωνα κατανέμονται διαφορετικά. Για αυτό το λόγο, η λευκή περιοχή των δύο τετραγώνων πρέπει να έχει ίσο εμβαδόν. Ο υπολογισμός των εμβαδών των λευκών περιοχών, οδηγεί στο πυθαγόρεια θεώρημα και αποδεικνύει το ζητούμενο.
Το γεγονός ότι αυτή η πολύ απλή απόδειξη αποδίδεται στον Πυθαγόρα, συχνά αναφέρεται σε συγγράμματα του μεταγενέστερου Έλληνα φιλόσοφου και μαθηματικού, Πρόκλου. Αρκετές ακόμα αποδείξεις του θεωρήματος περιγράφοντα παρακάτω, αλλά αυτή είναι γνωστή σαν πυθαγόρεια απόδειξη.
Άλλες μορφές του θεωρήματος[Επεξεργασία | επεξεργασία κώδικα]
Όπως ειπώθηκε και στην εισαγωγή, αν το γ αντιπροσωπεύει το μήκος της υποτείνουσας και τα α, β τα μήκη των δύο κάθετων πλευρών, το πυθαγόρειο θεώρημα μπορεί να εκφραστεί με τη μορφή της πυθαγόρειας εξίσωσης:
Αν τα μήκη α και β είναι γνωστά, τότε το γ μπορεί να υπολογιστεί ως εξής:
Αν το μήκος της υποτείνουσας (γ) και της μίας κάθετης πλευράς (α ή β) είναι γνωστά, τότε το μήκος της άλλης κάθετης πλευρά υπολογίζεται με τις ακόλουθες εξισώσεις:
ή
Η πυθαγόρεια εξίσωση συσχετίζει τις πλευρές ενός ορθογωνίου τριγώνου με απλό τρόπο, έτσι ώστε αν είναι γνωστά τα μήκη δύο πλευρών να μπορεί να υπολογισθεί το μήκος της τρίτης. Μία άλλη συνέπεια του θεωρήματος είναι ότι σε οποιοδήποτε ορθογώνιο τρίγωνο, η υποτείνουσα είναι μεγαλύτερη από κάθε κάθετη πλευρά αλλά μικρότερη από το άθροισμα τους.
Μία γενίκευση του θεωρήματος είναι ο νόμος των συνημιτόνων, που επιτρέπει τον υπολογισμό του μήκους κάθε πλευράς σε οποιοδήποτε τρίγωνο, εάν είναι γνωστά τα μήκη των δύο άλλων πλευρών και η γωνία που αυτές σχηματίζουν. Αν η γωνία των δύο αυτών πλευρών είναι ορθή, ο νόμος των συνημιτόνων ταυτίζεται με το πυθαγόρειο θεώρημα.
Άλλες αποδείξεις του θεωρήματος[Επεξεργασία | επεξεργασία κώδικα]
Το πυθαγόρειο θεώρημα ίσως έχει περισσότερες αποδείξεις από κάθε άλλο (με το θεμελιώδες θεώρημα της άλγεβρας να είναι επίσης υποψήφιο για αυτή τη διάκριση): το βιβλίο Η πυθαγόρεια πρόταση περιέχει 370 αποδείξεις.
Απόδειξη με ομοιότητα τριγώνων[Επεξεργασία | επεξεργασία κώδικα]

Η απόδειξη βασίζεται στο γεγονός ότι ο λόγος δύο οποιονδήποτε αντιστοίχων πλευρών ομοίων τριγώνων, είναι σταθερός, ανεξάρτητα από το μέγεθος των τριγώνων.
Έστω το ορθογώνιο τρίγωνο ΑΒΓ, με ορθή γωνία τη Γ όπως φαίνεται και στο σχήμα. Φέρω το ύψος από τη γωνία Γ και ονομάζω Η το σημείο τομής του με την ΑΒ. Το σημείο Η χωρίζει την υποτείνουσα σε δύο ευθύγραμμα τμήματα με μήκη δ και ε. Το καινούριο τρίγωνο ΑΓΗ είναι όμοιο με το τρίγωνο ΑΒΓ, αφού και τα δύο είναι ορθογώνια (λόγω του ορισμού του ύψους) και έχουν κοινή τη γωνία Α, πράγμα που σημαίνει ότι η τρίτη γωνία είναι επίσης ίση στα δύο τρίγωνα (στο σχήμα συμβολίζεται με θ). Ομοίως, το τρίγωνο ΓΒΗ είναι επίσης όμοιο με το ΑΒΓ. Η ομοιότητα των τριγώνων οδηγεί στην ισότητα των λόγων των αντίστοιχων πλευρών
και
Το πρώτο κλάσμα ισούται με το συνημίτονο της γωνίας θ και το δεύτερο με το ημίτονο.
Οι παραπάνω λόγοι μπορούν να γραφτούν και ως εξής:
και
Προσθέτοντας τις δύο ισότητες, καταλήγουμε:
Ο ρόλος αυτής της απόδειξης στην ιστορία είναι ένα θέμα για πολλή σκέψη. Το ερώτημα που προκύπτει είναι γιατί ο Ευκλείδης δεν χρησιμοποίησε αυτήν την απόδειξη, αλλά εφηύρε άλλη. Μία υπόθεση είναι ότι η απόδειξη με όμοια τρίγωνα συμπεριλαμβάνει μία θεωρία αναλογιών, η οποία δεν εμφανίζεται παρά μόνο αργότερα στα Στοιχεία και εκείνη την εποχή χρειαζόταν πολύ περισσότερη ανάπτυξη.
Απόδειξη του Ευκλείδη[Επεξεργασία | επεξεργασία κώδικα]

Σε γενικές γραμμές η απόδειξη στα Στοιχεία του Ευκλείδη αναπτύσσεται ως εξής: Το μεγάλο τετράγωνο χωρίζεται σε δύο ορθογώνια παραλληλόγραμμα. Κατασκευάζεται ένα τρίγωνο που έχει το μισό εμβαδόν του αριστερού ορθογωνίου. Στη συνέχεια κατασκευάζεται ένα άλλο τρίγωνο που έχει το μισό εμβαδόν του τετραγώνου πάνω αριστερά. Τα δύο αυτά τρίγωνα συμπίπτουν, αποδεικνύοντας ότι το αριστερό τετράγωνο έχει ίσο εμβαδόν με το αριστερό ορθογώνιο. Ομοίως το δεξί τετράγωνο έχει ίσο εμβαδόν με το δεξί ορθογώνιο. Σχηματίζοντας το αρχικό τετράγωνο στην υποτείνουσα, παρατηρείται ότι το εμβαδόν του ισούται με το άθροισμα των εμβαδών των δύο άλλων τετραγώνων. Ακολουθούν λεπτομέρειες.
Έστω A,B,C οι κορυφές ενός ορθογωνίου τριγώνου, με ορθή τη γωνία Α. Φέρνω μία κάθετη ευθεία από το Α στην πλευρά απέναντι από την υποτείνουσα,σ το τετράγωνο της υποτείνουσας. Η ευθεία αυτή χωρίζει το τετράγωνο σε δύο ορθογώνια, που το καθένα έχει ίσο εμβαδόν με ένα από τα τετράγωνα των δύο άλλων πλευρών.
Για την επίσημη απόδειξη, απαιτούνται τέσσερα βασικά λήμματα:
- Αν δύο τρίγωνα έχουν από δύο πλευρές τους ίσες μια προς μία και την περιεχόμενη γωνία ίση, ταυτίζονται (πλευρά-γωνία-πλευρά)
- Το εμβαδόν ενός τριγώνου είναι το μισό από το εμβαδόν ενός παραλληλογράμμου με την ίδια βάση και το ίδιο ύψος
- Το εμβαδόν ενός ορθογωνίου ισούται με το γινόμενο δύο διαδοχικών πλευρών του.
- Το εμβαδόν ενός τετραγώνου ισούται με το γινόμενο δύο πλευρών του.
Στη συνέχεια, κάθε ένα από τα τετράγωνα των κάθετων πλευρών σχετίζεται με ένα τρίγωνο το οποίο ταυτίζεται με ένα σχετιζόμενο με ένα από τα δύο ορθογώνια του τετραγώνου της υποτείνουσας τρίγωνο


Η απόδειξη έχει ως εξής:
- Έστω ΑΒC ένα ορθογώνιο τρίγωνο με ορθή τη γωνία CΑΒ.
- Σε καθεμία από τις πλευρές ΒC, ΑΒ και CΑ σχεδιάζονται τα τετράγωνα CBDE, BAGF και ACIH αντίστοιχα. Η κατασκευή των τετραγώνων βασίζεται στο αξίωμα της παραλληλίας.
- Από το Α, φέρω παράλληλη στις BD και CE. Αυτή θα τμήσει κάθετα τις BC και DE στα σημεία Κ και L αντίστοιχα.
- Φέρω τις CF και AD για να σχηματιστούν τα τρίγωνα BCF και BDA
- Οι γωνίες CAB και BAG είναι και οι δύο ορθές. Έτσι τα σημεία C, A και G είναι συγγραμικά. Ομοίως τα B, A και Η.
- Οι γωνίες CBD και FBA είναι και οι δύο ορθές. Επομένως η γωνία ABD ισούται με τη γωνία FBC, αφού και oi δύο είναι ίσες με το άθροισμα της ABC και μίας ορθής.
- Αφού AB=BF και BD=BC τα τρίγωνα ABD και FBC ταυτίζονται.
- Αφού η A-K-L είναι ευθεία παράλληλη στην BD, το ορθογώνιο BDLK έχει διπλάσιο εμβαδόν από το τρίγωνο ABD αφού έχουν κοινή βάση την BD και το ίδιο ύψος BK
- Αφού το C είναι συγγραμμικό με τα A και G, στο τετράγωνο BAGF πρέπει να έχει διπλάσιο εμβαδόν από το τρίγωνο FBC.
- Έτσι το ορθογώνιο BDLK πρέπει να έχει το ίδιο εμβαδόν με το τετράγωνο ABFG=AB2
- Ομοίως το ορθογώνιο CKLE έχει το ίδιο εμβαδόν με το τετράγωνο ACIH=AC2
- Προσθέτοντας τα δύο αποτελέσματα,
- Αφού BD=KL,
- Έτσι , αφού CBDE τετράγωνο.
Η απόδειξη αυτή, που εμφανίζεται στα Στοιχεία του Ευκλείδη, υποδεικνύει ότι το εμβαδόν του τετραγώνου της υποτείνουσας ισούται με το άθροισμα των τετραγώνων των δύο κάθετων πλευρών. Αυτό είναι ξεκάθαρο και από την απόδειξη με όμοια τρίγωνα που φημολογείται ότι χρησιμοποιούσε ο Πυθαγόρας.
Απόδειξη με ανακατανομή[Επεξεργασία | επεξεργασία κώδικα]
Έχει γίνει ήδη αναφορά στην πυθαγόρεια απόδειξη, η οποία είναι απόδειξη με ανακατανομή. Η ίδια ιδέα εκφράζεται από την κινούμενη εικόνα, η οποία αποτελείται από ένα μεγάλο τετράγωνο, πλευράς a+b, που περιέχει τέσσερα όμοια ορθογώνια τρίγωνα. Τα τρίγωνα εμφανίζοντα σε δύο κατανομές, η πρώτη από τις οποίες αφήνει ακάλυπτη μία περιοχή που αποτελείται από δύο τετράγωνα, πλευράς a και b και η δεύτερη ένα τετράγωνο πλευράς c. Το εμβαδόν του εξωτερικού τετραγώνου δεν αλλάζει, όπως και το εμβαδόν των τεσσάρων τριγώνων, επομένως προκύπτει ότι a2 + b2 = c2.

Μία δεύτερη απόδειξη ανακατανομής δίνεται στην δεύτερη κινούμενη εικόνα. Σχηματίζεται ένα μεγάλο τετράγωνο πλευράς c, από τέσσερα πανομοιότυπα ορθογώνια τρίγωνα πλευράς a,b και c, γύρω από ένα μικρό κεντρικό τετράγωνο. Στη συνέχεια σχηματίζονται δύο ορθογώνια παραλληλόγραμμα πλευράς a και b με μετακίνηση των τριγώνων. Ο συνδυασμός του μικρού τετραγώνου με τα δύο παραλληλόγραμμα παράγει δύο τετράγωνα με εμβαδά a2 και b2, τα οποία έχουν ίσο εμβαδόν με το αρχικό μεγάλο τετράγωνο.

Η τρίτη κινούμενη απόδειξη δίνει ακόμα μία απόδειξη. Τα πάνω τετράγωνα χωρίζονται όπως φαίνεται στην εικόνα με μπλε και πράσινη σκιαγράφηση, σε κομμάτια τα οποία αν επανατοποθετηθούν μπορούν να σχηματίσουν το τετράγωνο της υποτείνουσας- ή αντίστροφα το μεγάλο τετράγωνο μπορεί να χωριστεί σε κομμάτια που σχηματίζουν τα δύο άλλα. Αυτό αποδεικνύει ότι το εμβαδόν του μεγάλου τετραγώνου ισούται με αυτό των άλλων δύο.

Αλγεβρικές αποδείξεις[Επεξεργασία | επεξεργασία κώδικα]

Το θεώρημα μπορεί να αποδειχθεί αλγεβρικά χρησιμοποιώντας τέσσερα ορθογώνια τρίγωνα με πλευρές a,b και c, τοποθετημένες μέσα σε ένα τετράγωνο πλευράς c όπως στο πάνω σχήμα. Τα τρίγωνα είναι ίδια με εμβαδόν , ενώ το μικρό τετράγωνο έχει πλευρά b-a και εμβαδόν . Επομένως το εμβαδόν του μεγάλου τετραγώνου είναι:
Αλλά είναι τετράγωνο πλευράς c και εμβαδού c2, οπότε
Μία παρόμοια απόδειξη χρησιμοποιεί τέσσερα ίδια τρίγωνα τοποθετημένα συμμετρικά γύρω από ένα τετράγωνο πλευράς c. Έτσι δημιουργείται ένα μεγαλύτερο τετράγωνο με πλευρά a+b και εμβαδόν (a + b)2. Τα τέσσερα τρίγωνα και το τετράγωνο πλευράς c πρέπει να έχουν ίσο εμβαδόν με το μεγαλύτερο τετράγωνο,
επομένως

Μία σχετική απόδειξη είχε εκδώσει ο μετέπειτα πρόεδρος των ΗΠΑ, James Abram Garfield. Αντί για τετράγωνο, χρησιμοποίησε ένα τραπέζιο, το οποίο μπορεί να κατασκευαστεί από το τετράγωνο της δεύτερης από τις παραπάνω αποδείξεις, φέρνοντας μία διαγώνιο του εσωτερικού τετραγώνου, ώστε να κατασκευαστεί το τραπέζιο που φαίνεται στο σχήμα. Το εμβαδόν του τραπεζίου είναι το μισό από αυτό του τετραγώνου και υπολογίζεται από τη σχέση
Η απόδειξη είναι όμοια με την προηγούμενη, εκτός από την εμφάνιση του παράγοντα που απαλείφεται αν πολλαπλασιάσω τα δύο μέλη με 2.
Απόδειξη με χρήση διαφορικών[Επεξεργασία | επεξεργασία κώδικα]

Μπορεί κανείς να καταλήξει στο πυθαγόρειο θεώρημα μελετώντας πώς αλλαγές σε μία πλευρά του τριγώνου επηρεάζουν την υποτείνουσα, και εμπλέκοντας το λογισμό.
Το τρίγωνο ABC είναι ορθογώνιο όπως φαίνεται στο σχήμα, με υποτείνουσα την BC. Η υποτείνουσα έχει μήκος y, η πλευρά AC έχει μήκος x και η AB μήκος a.
Όσο αυξάνεται το x κατά μία μικρή ποσότητα dx, επεκτείνοντας ελαφρώς την AC προς το D, αυξάνεται και το y κατά μία ποσότητα dy. Σχηματίζονται έτσι δύο πλευρές ενός τριγώνου CDE (με Ε τέτοιο ώστε η CE να είναι κάθετη στην υποτείνουσα), το οποίο είναι ορθογώνια και προσεγγιστικά πανομοιότυπο με το ABC. Επομένως ο λόγος των πλευρών τους πρέπει να είναι σταθερός
ή
Η λύση της διαφορικής αυτής εξίσωσης είναι:
Για x=0 y=a,
Η παραπάνω απόδειξη δεν είναι επίσημη.
Αντίστροφο[Επεξεργασία | επεξεργασία κώδικα]
Ισχύει και το αντίστροφο του θεωρήματος:
Για κάθε θετικούς αριθμούς α,β και γ τέτοιους ώστε α2+β2=γ2, υπάρχει τρίγωνο με πλευρές α,β και γ, και σε κάθε τέτοια τρίγωνο η γωνία που σχηματίζουν οι πλευρές α και β είναι ορθή.
Το αντίστροφο εμφανίζεται και στα στοιχεία του Ευκλείδη:
"Αν σε ένα τρίγωνο το τετράγωνο της μίας πλευράς ισούται με το άθροισμα των τετραγώνων των δύο άλλων πλευρών, τότε η γωνία που αυτές σχηματίζουν είναι ορθή"
Αποδεικνύεται με το νόμο των συνημιτόνων ή ως εξής:
Έστω ΑΒΓ, τρίγωνο με πλευρές α,β,γ και α2+β2=γ2. Κατασκευάζω ένα δεύτερο τρίγωνο με πλευρές μήκους α και β που να σχηματίζουν ορθή γωνία. Τότε λόγω του θεωρήματος, για την υποτείνουσα αυτού του τριγώνου ισχύει:
, που ισούται με την υποτείνουσα του πρώτου τριγώνου. Αφού τα τρίγωνα έχουν ίσα μήκη πλευρών, τα τρίγωνα ταυτίζονται και πρέπει να έχουν ίσες γωνίες. Επομένως, η γωνία μεταξύ των πλευρών α και β στο αρχικό τρίγωνο είναι ορθή.
Η παραπάνω απόδειξη χρησιμοποιεί το ίδιο το πυθαγόρειο θεώρημα. Το αντίστροφο μπορεί να αποδειχθεί και χωρίς χρήση του θεωρήματος.
Το αντίστροφο του πυθαγορείου θεωρήματος έχει επίσης οδηγήσει σε έναν απλό τρόπο διαπίστωσης εάν ένα τρίγωνο είναι ορθογώνιο, οξυγώνιο ή αμβλυγώνιο. Έστω γ η μεγαλύτερη πλευρά του τριγώνου και α+β>γ (τριγωνική ανισότητα)
- Αν α2+β2=γ2, τότε το τρίγωνο είναι ορθογώνιο
- Αν α2+β2<γ2, τότε το τρίγωνο είναι αμβλυγώνιο
- Αν α2+β2>γ2, τότε το τρίγωνο είναι οξυγώνιο
Συνέπειες και χρήσεις του πυθαγορείου θεωρήματος[Επεξεργασία | επεξεργασία κώδικα]
Πυθαγόρειες τριάδες[Επεξεργασία | επεξεργασία κώδικα]
Μία πυθαγόρεια τριάδα αποτελείται από τρεις θετικούς ακέραιους αριθμούς α,β,γ τέτοιους ώστε α2+β2=γ2 . Με άλλα λόγια μία αντιπροσωπεύει τα μήκη των πλευρών ενός ορθογωνίου τριγώνου, όταν αυτά είναι ακέραιοι αριθμοί. Στοιχεία από μεγαλιθικά μνημεία της Βόρειας Ευρώπης δείχνουν ότι τέτοιες τριάδες ήταν γνωστές πολύ πριν την ανακάλυψη της γραφής.Τέτοιες τριάδες γράφονται συνήθως (α,β,γ). Οι γνωστότερες είναι (3,4,5) και (5,12,13).
Μία αρχέγονη πυθαγόρεια τριάδα είναι αυτή για την οποία οι α,β,γ είναι πρώτοι μεταξύ τους (δηλαδή ο μέγιστος κοινός διαιρέτης των α,β,γ είναι 1).
Παρακάτω είναι μία λίστα με αρχέγονες πυθαγόρειες τριάδες με αριθμούς μικρότερους του 100:
(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16,63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)
Μη μετρήσιμα μήκη[Επεξεργασία | επεξεργασία κώδικα]

Μία από τις συνέπειες του πυθαγορείου θεωρήματος είναι ότι ευθύγραμμα τμήματα των οποίων τα μήκη είναι μη μετρήσιμα (όπως οι ρίζες), μπορούν να κατασκευαστούν με χάρακα και διαβήτη. Το θεώρημα του Πυθαγόρα επιτρέπει την κατασκευή μη μετρήσιμων μηκών εξ'αιτίας του ότι συσχετίζονται τα τετράγωνα της υποτείνουσας και των δύο κάθετων πλευρών.
Το σχέδιο δεξιά δείχνει πως κατασκευάζονται ευθύγραμμα τμήματα με μήκη τετραγωνικές ρίζες οποιωνδήποτε θετικών ακεραίων. Κάθε τρίγωνο έχει μία πλευρά (συμβολίζεται με "1") που θεωρείται μοναδιαία για τη μέτρηση. Σε κάθε ορθογώνιο τρίγωνο, το πυθαγόρειο θεώρημα συσχετίζει το μήκος της υποτείνουσας με την πλευρά που θεωρείται μοναδιαία, και αν οι πλευρές του τριγώνου είναι ρίζες μη τέλειων τετραγώνων, κατασκευάζονται έτσι μη μετρήσιμα μήκη.
Τα μη μετρήσιμα μήκη έρχεται σε αντιπαράθεση με την θεώρηση των αριθμών από τον Πυθαγόρα που συμπεριλαμβάνει μόνο ακέραιους αριθμούς. Ο Πυθαγόρας, ασχολήθηκε με αναλογίες συγκρίνοντας τα κλάσματα με άλλα όπου ο αριθμητής ήταν ακέραιο πολλαπλάσιο του κοινού παρονομαστή.
Μιγαδικοί αριθμοί[Επεξεργασία | επεξεργασία κώδικα]

Για κάθε μιγαδικό αριθμό
το μέτρο δίνεται από τον τύπο
Οπότε οι τρεις ποσότητες, r, x και y συσχετίζονται με την πυθαγόρεια εξίσωση,
Το r ορίζεται ως ένα μη αρνητικός αριθμός αλλά δεν υπάρχει περιορισμός για τα x και y. Γεωμετρικά το r είναι η απόσταση του z από την αρχή των αξόνων στο μιγαδικό επίπεδο.
Αυτό μπορεί να γενικευτεί για να βρεθεί η απόσταση δύο σημείων z1 και z2. Η απόσταση αυτή δίνεται από τον τύπο
και η σχέση αυτή παίρνει επίσης τη μορφή της πυθαγόρειας εξίσωσης,
Ευκλείδεια απόσταση σε διάφορα συστήματα συντεταγμένων[Επεξεργασία | επεξεργασία κώδικα]
Ο τύπος της απόστασης στο καρτεσιανό σύστημα συντεταγμένων βασίζεται στο πυθαγόρειο θεώρημα. Αν (x1, y1) και (x2, y2) είναι σημεία του επιπέδου, τότε η απόσταση μεταξύ τους, που ονομάζεται και ευκλείδεια απόσταση, δίνεται από τον τύπο:
Πιο γενικά, στου ευκλείδειους ν-διάστατους χώρους, η απόσταση μεταξύ δύο σημείων and , ορί
Αν αντί για καρτεσιανές χρησιμοποιούνται άλλες συντεταγμένες, για παράδειγμα πολικές, οι τύποι της απόστασης είναι πιο πολύπλοκοι αλλά πάλι βασίζονται στο πυθαγόρειο θεώρημα. Για παράδειγμα, οι πολικές συντεταγμένες (r, θ) μπορούν στο καρτεσιανό επίπεδο να γραφούν ως:
Τότε η απόσταση s μεταξύ δύο σημείων με συντεταγμένες (r1, θ1) και (r2, θ2) είναι:
Έτσι η απόσταση σε πολικές συντεταγμένες δίνεται από τον τύπο:
Ο τύπος αυτός είναι ο νόμος των συνημιτόνων, που ονομάζεται και γενικευμένο πυθαγόρειο θεώρημα. Σε περίπτωση που η γωνία είναι ορθή, δηλαδή Δθ = π/2, επανερχόμαστε στο πυθαγόρειο θεώρημα: Επομένως, το Πυθαγόρειο θεώρημα που ισχύει μόνο για ορθές γωνίες, είναι μία υποπερίπτωση του γενικότερου νόμου των συνημιτόνων που ισχύει για οποιαδήποτε γωνία.
Πυθαγόρεια τριγωνομετρική ταυτότητα[Επεξεργασία | επεξεργασία κώδικα]

Σε ένα ορθογώνιο τρίγωνο με πλευρές a, b και υποτείνουσα c, η τριγωνομετρία ορίζει ότι το ημίτονο (sin) και το συνημίτονο (cos) της γωνίας θ μεταξύ της πλευράς a και της υποτείνουσας είναι:
Έτσι:
όπου εφαρμόζεται το πυθαγόρειο θεώρημα. Η σχέση αυτή μεταξύ ημιτόνου και συνημιτόνου ονομάζεται θεμελιώδης τριγωνομετρική ταυτότητα. Στα όμοια τρίγωνα ο λόγος των πλευρών δεν εξαρτάται από το μέγεθος του τριγώνου αλλά από τις γωνίες. Στο σχήμα, sτο τρίγωνο με τη μοναδιαία υποτείνουσα, η γωνία θ έχει απέναντι πλευρά την sin θ και προσκείμενη πλευρά την cos θ
Σχέση με το εξωτερικό γινόμενο[Επεξεργασία | επεξεργασία κώδικα]

Το πυθαγόρειο θεώρημα συσχετίζει το εξωτερικό και το εσωτερικό γινόμενο δύο διανυσμάτων με τον τύπο:
Με τα εξωτερικό και εσωτερικό γινόμενο να ορίζονται ως εξής:
με n ένα μοναδιαίο διάνυσμα κάθετο στα a και b. Η παραπάνω σχέση προκύπτει τους ορισμούς και την πυθαγόρεια τριγωνομετρική ταυτότητα.
Με ανακατανομή της παραπάνω σχέσης, προκύπτει:
Η σχέση αυτή μπορεί να θεωρηθεί ως προϋπόθεση του εξωτερικού γινομένου και άρα μέρος του ορισμού του.
Οι γενικεύσεις[Επεξεργασία | επεξεργασία κώδικα]
Παρόμοια στοιχεία στις τρεις πλευρές[Επεξεργασία | επεξεργασία κώδικα]
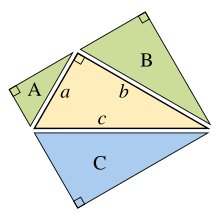
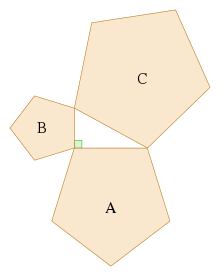
Μία γενίκευση του Πυθαγορείου θεωρήματος που επεκτείνεται πέρα από τους τομείς των τετραγώνων στις τρεις πλευρές σε παρόμοια στοιχεία έγινε γνωστή από τον Ιπποκράτη της Χίου τον πέμπτο αιώνα π.Χ., και συγκαταλέχθηκε από τον Ευκλείδη στα Στοιχεία :
Αν κάποιος ορθώνει παρόμοια στοιχεία (βλέπε Ευκλείδεια γεωμετρία) με αντίστοιχες πλευρές στις πλευρές ενός ορθογωνίου τριγώνου, τότε το άθροισμα των εμβαδών των δύο μικρότερων πλευρών ισούται με το εμβαδόν της μεγαλύτερης πλευράς.
Η επέκταση αυτή προϋποθέτει ότι οι πλευρές του αρχικού τριγώνου είναι οι αντίστοιχες πλευρές των τριών συγκεκλιμένων στοιχείων (έτσι ώστε οι κοινές αναλογίες των πλευρών μεταξύ τον όμοιων στοιχείων είναι a:b:c).Και ενώ η απόδειξη του Ευκλείδη εφαρμόζεται μόνο σε κυρτά πολύγωνα, το θεώρημα ισχύει και για κοίλα πολύγωνα ακόμη και σε παρόμοια στοιχεία που έχουν καμπύλα όρια (αλλά ακόμη με μέρος του ορίου ενός στοιχείου να παραμένει πλευρά του αρχικού τριγώνου).
Η βασική ιδέα πίσω από τις γενικεύσεις είναι ότι το εμβαδόν ενός επίπεδου στοιχείου είναι ανάλογο του τετραγώνου της κάθε γραμμικής διάστασης, και συγκεκριμένα είναι ανάλογο του τετραγώνου του μήκους της κάθε πλευράς. Έτσι, αν παρόμοια στοιχεία με εμβαδά A,B και C ανεγερθούν σε πλευρές με αντίστοιχα μήκη a,b και c τότε:
,
.
Αλλά, σύμφωνα με το Πυθαγόρειο θεώρημα, ,έτσι A + B = C.
Αντίστροφα, αν αποδείξουμε ότι Α + Β = C για τρία παρόμοια στοιχεία χωρίς να χρησιμοποιήσουμε το Πυθαγόρειο θεώρημα, τότε μπορούμε να δουλέψουμε ανάποδα για να κατασκευάσουμε μία απόδειξη του θεωρήματος. Για παράδειγμα, το αρχικό τρίγωνο μπορεί να αντιγραφεί και να χρησιμοποιηθεί ως ένα τρίγωνο C στην υποτείνουσά του, και δύο όμοια ορθογώνια τρίγωνα (Α και Β) κατασκευασμένα στις άλλες δύο πλευρές, σχεδιασμένα από το διαχωρισμό του αρχικού τριγώνου με βάση τα ύψη του. Ως εκ τούτου, το άθροισμα των εμβαδών των δύο μικρότερων τριγώνων είναι αυτό του τρίτου, έτσι Α + Β = C και αντιστρέφοντας την παραπάνω λογική οδηγούμαστε στο Πυθαγόρειο θεώρημα .
 |
 |
 |
Νόμος των συνημιτόνων[Επεξεργασία | επεξεργασία κώδικα]

Το Πυθαγόρειο θεώρημα είναι μία ειδική περίπτωση ενός γενικευμένου θεωρήματος το οποίο σχετίζεται με τα μήκη των πλευρών οποιουδήποτε τριγώνου, και που είναι γνωστό ως ο νόμος των συνημιτόνων. Σε έναν τρίγωνο με πλευρές , και , ισχύει ότι
- ,
όπου είναι η γωνία μεταξύ των πλευρών και .
Όταν η γωνία είναι μοίρες, τότε και ο τύπος δίνει το Πυθαγόρειο θεώρημα.
Διανυσματικός χώρος με εσωτερικό γινόμενο[Επεξεργασία | επεξεργασία κώδικα]
Σε οποιονδήποτε διανυσματικό χώρο με εσωτερικό γινόμενο , το πυθαγόρειο θεώρημα γενικεύεται ως εξής. Για κάθε δύο διανύσματα που είναι κάθετα μεταξύ τους, δηλαδή , ισχύει ότι[2]:66[3]:32
- ,
όπου και .
Η απόδειξη έπεται από τις ιδιότητες του εσωτερικού γινομένου:
Στη λαϊκή κουλτούρα[Επεξεργασία | επεξεργασία κώδικα]

Το Πυθαγόρειο θεώρημα έχει επικρατήσει στον δημοφιλή πολιτισμό με διάφορους τρόπους.
- Ο Hans Christian Andersen έγραψε το 1831 ένα ποίημα σχετικό με το Πυθαγόρειο θεώρημα: Formens Evige Magie (Et poetisk Spilfægteri).
- Μία εκδοχή του Major-General's Song στην κωμική όπερα The Pirates of Penzance των Gilbert και Sullivan, "Σχετικά με το διωνυμικό θεώρημα είμαι γεμάτος με πολλές ειδήσεις, με πολλά χαρούμενα γεγονότα σχετικά με το τετράγωνο της υποτείνουσας", κάνει μία πλάγια αναφορά στο θεώρημα.
- Ο Scarecrow στην ταινία Ο μάγος του Οζ κάνει μία πιο συγκεκριμένη αναφορά στο θεώρημα. Μετά τη λήψη του διπλώματός του από τον Μάγο, επιδεικνύει τις "γνώσεις" του απαγγέλοντας μία εσφαλμένη και παραμορφωμένη εκδοχή του θεωρήματος: "Το άθροισμα των τετραγωνικών ριζών οποιωνδήποτε πλευρών ενός ισοσκελούς τριγώνου είναι ίσο με την τετραγωνική ρίζα της εναπομείνασας πλευράς. Ω,χαρά!Ω,έκσταση! Έχω μυαλό!".
- Το 2000, στην Ουγκάντα κυκλοφόρησε ένα νόμισμα με τη μορφή ενός ισοσκελούς ορθογωνίου τριγώνου. Η μία πλαυρά του νομίσματος έχει την εικόνα του Πυθαγόρα και την εξίσωση , συνοδευόμενα από την αναφορά "ΧΙΛΙΕΤΙΑ ΤΟΥ ΠΥΘΑΓΟΡΑ".
- Στην Ελλάδα, την Ιαπωνία, το Σαν Μαρίνο, τη Σιέρα Λεόνε και το Σουρινάμ έχουν κυκλοφορήσει γραμματόσημα που απεικονίζουν τον Πυθαγόρα και το Πυθαγόρειο θεώρημα.
- Στου Neal Stephenson τη θεωρητική μυθιστοριματική Anathem, το Πυθαγόρειο θεώρημα αναφέρεται ως 'the Adrakhonic theorem'. Μία γεωμετρική απόδειξη του θεωρήματος εκτίθεται στην πλευρά ενός εξωγήινου σκάφους για να προβάλει την κατανόηση των μαθηματικών από τους εξωγήινους.
Όλο το θεώρημα[Επεξεργασία | επεξεργασία κώδικα]
ἐν τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν γωνίαν περιεχουσῶν πλευρῶν τετραγώνοις. ἔστω τρίγωνον ὀρθογώνιον τὸ ΑΒΓ ὀρθὴν ἔχον τὴν ὑπὸ ΒΑΓ γωνίαν· λέγω, ὅτι τὸ ἀπὸ τῆς ΒΓ τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ τετραγώνοις.[4][1][5]
ἀναγεγράφθω γὰρ ἀπὸ μὲν τῆς ΒΓ τετράγωνον τὸ ΒΔΕΓ, ἀπὸ δὲ τῶν ΒΑ, ΑΓ τὰ ΗΒ, ΘΓ, καὶ διὰ τοῦ Α ὁποτέρᾳ τῶν ΒΔ, ΓΕ παράλληλος ἤχθω ἡ ΑΛ· καὶ ἐπεζεύχθωσαν αἱ ΑΔ, ΖΓ. καὶ ἐπεὶ ὀρθή ἐστιν ἑκατέρα τῶν ὑπὸ ΒΑΓ, ΒΑΗ γωνιῶν, πρὸς δή τινι εὐθείᾳ τῇ ΒΑ καὶ τῷ πρὸς αὐτῇ σημείῳ τῷ Α δύο εὐθεῖαι αἱ ΑΓ, ΑΗ μὴ ἐπὶ τὰ αὐτὰ μέρη κείμεναι τὰς ἐφεξῆς γωνίας δυσὶν ὀρθαῖς ἴσας ποιοῦσιν· ἐπ᾽ εὐθείας ἄρα ἐστὶν ἡ ΓΑ τῇ ΑΗ. διὰ τὰ αὐτὰ δὴ καὶ ἡ ΒΑ τῇ ΑΘ ἐστιν ἐπ᾽ εὐθείας. καὶ ἐπεὶ ἴση ἐστὶν ἡ ὑπὸ ΔΒΓ γωνία τῇ ὑπὸ ΖΒΑ —ὀρθὴ γὰρ ἑκατέρα— κοινὴ προσκείσθω ἡ ὑπὸ ΑΒΓ· ὅλη ἄρα ἡ ὑπὸ ΔΒΑ ὅλῃ τῇ ὑπὸ ΖΒΓ ἐστιν ἴση. καὶ ἐπεὶ ἴση ἐστὶν ἡ μὲν ΔΒ τῇ ΒΓ, ἡ δὲ ΖΒ τῇ ΒΑ, δύο δὴ αἱ ΔΒ, ΒΑ δύο ταῖς ΖΒ, ΒΓ ἴσαι εἰσὶν ἑκατέρα ἑκατέρᾳ· καὶ γωνία ἡ ὑπὸ ΔΒΑ γωνίᾳ τῇ ὑπὸ ΖΒΓ ἴση· βάσις ἄρα ἡ ΑΔ βάσει τῇ ΖΓ {ἐστιν} ἴση, καὶ τὸ ΑΒΔ τρίγωνον τῷ ΖΒΓ τριγώνῳ ἐστὶν ἴσον· καὶ {ἐστι} τοῦ μὲν ΑΒΔ τριγώνου διπλάσιον τὸ ΒΛ παραλληλόγραμμον· βάσιν τε γὰρ τὴν αὐτὴν ἔχουσι τὴν ΒΔ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΒΔ, ΑΛ· τοῦ δὲ ΖΒΓ τριγώνου διπλάσιον τὸ ΗΒ τετράγωνον· βάσιν τε γὰρ πάλιν τὴν αὐτὴν ἔχουσι τὴν ΖΒ καὶ ἐν ταῖς αὐταῖς εἰσι παραλλήλοις ταῖς ΖΒ, ΗΓ. {τὰ δὲ τῶν ἴσων διπλάσια ἴσα ἀλλήλοις ἐστίν·} ἴσον ἄρα ἐστὶ καὶ τὸ ΒΛ παραλληλόγραμμον τῷ ΗΒ τετραγώνῳ. ὁμοίως δὴ ἐπιζευγνυμένων τῶν ΑΕ, ΒΚ δειχθήσεται καὶ τὸ ΓΛ παραλληλόγραμμον ἴσον τῷ ΘΓ τετραγώνῳ· ὅλον ἄρα τὸ ΒΔΕΓ τετράγωνον δυσὶ τοῖς ΗΒ, ΘΓ τετραγώνοις ἴσον ἐστίν. καί ἐστι τὸ μὲν ΒΔΕΓ τετράγωνον ἀπὸ τῆς ΒΓ ἀναγραφέν, τὰ δὲ ΗΒ, ΘΓ ἀπὸ τῶν ΒΑ, ΑΓ. τὸ ἄρα ἀπὸ τῆς ΒΓ πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν ΒΑ, ΑΓ πλευρῶν τετραγώνοις. ἐν ἄρα τοῖς ὀρθογωνίοις τριγώνοις τὸ ἀπὸ τῆς τὴν ὀρθὴν γωνίαν ὑποτεινούσης πλευρᾶς τετράγωνον ἴσον ἐστὶ τοῖς ἀπὸ τῶν τὴν ὀρθὴν {γωνίαν} περιεχουσῶν πλευρῶν τετραγώνοις· ὅπερ ἔδει δεῖξαι.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 Gök. EUCLID'S ELEMENTS OF GEOMETRY.
- ↑ Αναστόπουλος, Χάρις. «Κβαντική Θεωρία» (PDF). Τμήμα Φυσικής, Πανεπιστήμιο Πατρών. Ανακτήθηκε στις 11 Σεπτεμβρίου 2022.
- ↑ Κολουντζάκης, Μ.· Παπαχριστόδουλος, Χ. (2015). Ανάλυση Fourier. Αθήνα: Κάλλιπος, Ανοικτές Ακαδημαϊκές Εκδόσεις. ISBN 978-960-603-360-5.
- ↑ «Το Πυθαγόρειο Θώρημα». pythagoras.samos.aegean.gr. Ανακτήθηκε στις 19 Σεπτεμβρίου 2023.
- ↑ «Euclid's Elements - Book 1 Postulate - Original Greek Text». www.physics.ntua.gr. Ανακτήθηκε στις 19 Σεπτεμβρίου 2023.
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- Anna M. Fraedrich: Die Satzgruppe des Pythagoras. Spektrum Akademischer Verlag, Heidelberg 1994. ISBN 3-86025-669-6
- Hans Schupp: Elementargeometrie. UTB, Stuttgart 1977. ISBN 3-506-99189-2
- Paul Karlson: Vom Zauber der Zahlen. Eine unterhaltsame Mathematik für Jedermann. Ullstein, Berlin 1954 (Zitate Proklos nach S. 103, 118).
- Egmont Colerus: Vom Einmaleins zum Integral. Mathematik für Jedermann. Rowohlt, Reinbek 1982. ISBN 3-499-16692-5
- Heinrich Tietze: Mathematische Probleme. Gelöste und ungelöste mathematische Probleme aus alter und neuer Zeit. Vierzehn Vorlesungen für Laien und Freunde der Mathematik. C.H. Beck, München 1990. ISBN 3-406-02535-8
- Wilhelm Capelle (Hrsg.): Die Vorsokratiker. Alfred Kröner, Stuttgart 1963. (Zitat Plutarch nach S. 102). ISBN 3-520-11908-0
- Alexander K. Dewdney: Reise in das Innere der Mathematik. Birkhäuser, Berlin 2000. ISBN 3-7643-6189-1
- Simon Singh: Fermats letzter Satz. dtv, München 2000. ISBN 3-423-33052-X
- Σωτήρης Χ. Γκουντουβάς, "Γεωμετρικές Διαδρομές", Αθήνα 2015
- Το Πυθαγόρειο θεώρημα δεν είναι του Πυθαγόρα τελικά... (Διαβάστε Άρθρο)
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Δεκάδες αποδείξεις του Πυθαγορείου θεωρήματος (αρχεία Geogebra)
- Απόδειξη του θεωρήματος (γερμανικά)
- Απόδειξη του θεωρήματος (αγγλικά)
- Java-Applets (αγγλικά)
- Διαδραστικό διδακτικό λογισμικό με απόδειξη, ασκήσεις και άλλους εξωτερικούς συνδέσμους
|







































































