Τετραγωνική ρίζα του 3

Η τετραγωνική ρίζα του 3 είναι ο θετικός πραγματικός αριθμός που, όταν πολλαπλασιαστεί με τον εαυτό του, δίνει τον αριθμό 3. Συμβολίζεται με ${\textstyle {\sqrt {3}}}$ ή $3^{1/2}$ . Ονομάζεται ακριβέστερα η κύρια τετραγωνική ρίζα του 3 για να διακρίνεται από τον αρνητικό αριθμό με την ίδια ιδιότητα. Η τετραγωνική ρίζα του 3 είναι ένας άρρητος αριθμός. Είναι επίσης γνωστή ως η σταθερά του Θεοδώρου, από τον Θεόδωρο τον Κυρηναίο που απέδειξε την αρρητότητά της.

Έως τον Δεκέμβριο του 2013, η αριθμητική της τιμή είχε υπολογιστεί σε τουλάχιστον δέκα δισεκατομμύρια ψηφία. Η δεκαδική της επέκταση, γραμμένη εδώ σε 60 δεκαδικά ψηφία, δίνεται από την ακολουθία A002194:

1.732050807568877293527446341505872366942805253810380628055806...

Το κλάσμα ${\textstyle {\frac {97}{56}}}$ ( 1.732142857...) μπορεί να χρησιμοποιηθεί ως καλή προσέγγιση. Παρόλο που έχει παρονομαστή μόνο το 56, διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {1}{10,000}}}$ (περίπου ${\textstyle 9.2\times 10^{-5}}$ , με σχετικό σφάλμα ${\textstyle 5\times 10^{-5}}$ ). Η στρογγυλοποιημένη τιμή του, 1.732, έχει σχετικό σφάλμα μόλις 0,01%.

Το κλάσμα ${\textstyle {\frac {716,035}{413,403}}}$ ( 1.73205080756...) έχει σχετικό σφάλμα ${\textstyle 1\times 10^{-11}}$ .

Ο Αρχιμήδης ανέφερε ένα εύρος για την τιμή της: ${\textstyle ({\frac {1351}{780}})^{2}>3>({\frac {265}{153}})^{2}}$ .^[1]

Το κατώτερο όριο ${\textstyle {\frac {1351}{780}}}$ είναι μια ακριβής προσέγγιση για το ${\sqrt {3}}$ που διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {1}{608,400}}}$ (έξι δεκαδικά ψηφία, σχετικό σφάλμα ${\textstyle 3\times 10^{-7}}$ ) και το ανώτατο όριο ${\textstyle {\frac {265}{153}}}$ διαφέρει από τη σωστή τιμή κατά λιγότερο από ${\textstyle {\frac {2}{23,409}}}$ (τέσσερα δεκαδικά ψηφία, σχετικό σφάλμα ${\textstyle 1\times 10^{-5}}$ ).

Σχέσεις[Επεξεργασία | επεξεργασία κώδικα]

Το ${\sqrt {3}}$ μπορεί να εκφραστεί ως το συνεχές κλάσμα [1; 1, 2, 1, 2, 1, 2, 1, …] (ακολουθία A040001 στην OEIS).

Είναι αλήθεια λοιπόν να πούμε ότι:

{\begin{bmatrix}1&2\\1&3\end{bmatrix}}^{n}={\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}}

οπότε, καθώς $n\to \infty$ :

{\sqrt {3}}=2\cdot {\frac {a_{22}}{a_{12}}}-1

.

Γεωμετρία και τριγωνομετρία[Επεξεργασία | επεξεργασία κώδικα]

Το ύψος ενός ισόπλευρου τριγώνου με μήκος πλευράς 2 είναι ίσο με √3. Επίσης, η πλευρά αυτή είναι η υποτείνουσα ενός τριγώνου 30-60-90 με μήκος 2.

Το ύψος ενός κανονικού εξαγώνου με πλευρές μήκους 1 είναι ίσο με √3.

Η τετραγωνική ρίζα του 3 μπορεί να βρεθεί ως το μήκος της καθέτου ενός ισόπλευρου τριγώνου που περιλαμβάνει έναν κύκλο με διάμετρο 1.

Εάν ένα ισόπλευρο τρίγωνο με πλευρές μήκους 1 κοπεί σε δύο ίσα μισά, διχοτομώντας μια εσωτερική γωνία για να σχηματιστεί μια ορθή γωνία στη μία πλευρά, η υποτείνουσα του τριγώνου της ορθής γωνίας έχει μήκος ένα και οι πλευρές του έχουν μήκος ${\textstyle {\frac {1}{2}}}$ και ${\textstyle {\frac {\sqrt {3}}{2}}}$ . Από αυτό, ${\textstyle \tan {60^{\circ }}={\sqrt {3}}}$ , ${\textstyle \sin {60^{\circ }}={\frac {\sqrt {3}}{2}}}$ και ${\textstyle \cos {30^{\circ }}={\frac {\sqrt {3}}{2}}}$ .

Η τετραγωνική ρίζα του 3 εμφανίζεται επίσης σε αλγεβρικές σχέσεις για διάφορες άλλες τριγωνομετρικές σταθερές, συμπεριλαμβανομένων^[2] των ημιτόνων των 3°, 12°, 15°, 21°, 24°, 33°, 39°, 48°, 51°, 57°, 66°, 69°, 75°, 78°, 84° και 87°.

Είναι η απόσταση μεταξύ των παράλληλων πλευρών ενός κανονικού εξαγώνου με πλευρές μήκους 1.

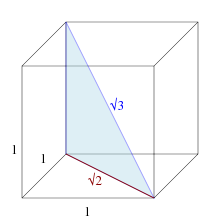
Είναι το μήκος της διαγωνίου ενός μοναδιαίου κύβου.

Άλλες χρήσεις και εμφανίσεις[Επεξεργασία | επεξεργασία κώδικα]

Δυναμική μηχανική[Επεξεργασία | επεξεργασία κώδικα]

Στην δυναμική μηχανική, η τάση μεταξύ δύο φάσεων σε ένα τριφασικό σύστημα είναι ίση με ${\textstyle {\sqrt {3}}}$ φορές τη γραμμή προς την ουδέτερη τάση. Αυτό συμβαίνει επειδή οποιεσδήποτε δύο φάσεις απέχουν 120° μεταξύ τους και δύο σημεία σε έναν κύκλο με απόσταση 120 μοιρών χωρίζονται μεταξύ τους με ${\textstyle {\sqrt {3}}}$ φορές την ακτίνα (δείτε παραδείγματα γεωμετρίας παραπάνω).

Ειδικές συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]

Είναι γνωστό ότι οι περισσότερες ρίζες της ν-οστής παραγώγου της $J_{\nu }^{(n)}(x)$ (όπου n < 18 και $J_{\nu }(x)$ είναι η συνάρτηση Μπέσελ πρώτου τύπου τάξης $\nu$ ) είναι υπερβατικές. Οι μόνες εξαιρέσεις είναι οι αριθμοί $\pm {\sqrt {3}}$ , που είναι οι αλγεβρικές ρίζες της $J_{1}^{(3)}(x)$ και της $J_{0}^{(4)}(x)$ .^[3]

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]

↑ Knorr, Wilbur R. (June 1976). «Archimedes and the measurement of the circle: a new interpretation». Archive for History of Exact Sciences 15 (2): 115–140. doi:10.1007/bf00348496. MR 0497462. https://link.springer.com/article/10.1007/BF00348496. Ανακτήθηκε στις November 15, 2022.
↑ Wiseman, Julian D. A. (Ιουνίου 2008). «Sin and Cos in Surds». JDAWiseman.com. Ανακτήθηκε στις 15 Νοεμβρίου 2022.
↑ Lorch, Lee; Muldoon, Martin E. (1995). «Transcendentality of zeros of higher dereivatives of functions involving Bessel functions». International Journal of Mathematics and Mathematical Sciences 18 (3): 551–560. doi:10.1155/S0161171295000706.

Commons logo

Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα
Τετραγωνική ρίζα του 3

[1] Knorr, Wilbur R. (June 1976). «Archimedes and the measurement of the circle: a new interpretation». Archive for History of Exact Sciences 15 (2): 115–140. doi:10.1007/bf00348496. MR 0497462. https://link.springer.com/article/10.1007/BF00348496. Ανακτήθηκε στις November 15, 2022.

[2] Wiseman, Julian D. A. (Ιουνίου 2008). «Sin and Cos in Surds». JDAWiseman.com. Ανακτήθηκε στις 15 Νοεμβρίου 2022.

[lorch-3] Lorch, Lee; Muldoon, Martin E. (1995). «Transcendentality of zeros of higher dereivatives of functions involving Bessel functions». International Journal of Mathematics and Mathematical Sciences 18 (3): 551–560. doi:10.1155/S0161171295000706.

[1]

[2]

[3]