Δύναμη (μαθηματικά)
Η δύναμη είναι μαθηματική πράξη, που συμβολίζεται ως αn και περιλαμβάνει δύο αριθμούς, την βάση α και τον εκθέτη n. Όταν το n είναι θετικός αριθμός, η δύναμη αντιστοιχεί σε επαναλαμβανόμενο (ή μεγάλο) πολλαπλασιασμό, με άλλα λόγια δύναμη είναι το γινόμενο n παραγόντων, ο καθένας από τους οποίους ισούται με α:
Κατά τον ίδιο τρόπο που ο πολλαπλασιασμός αντιστοιχεί σε επαναλαμβανόμενη (ή μεγάλη) πρόσθεση:
Ο εκθέτης είναι γραμμένος δεξιά της βάσης. Η δύναμη αn μπορεί να διαβαστεί ως α στη νιοστή δύναμη ή απλά α στη νιοστή. Κάποιοι εκθέτες έχουν ιδιαιτερότητες στην ανάγνωση: για παράδειγμα το α2 διαβάζεται συνήθως α στο τετράγωνο και το α3, α στον κύβο.
Η δύναμη αn μπορεί να οριστεί και όταν το n είναι αρνητικός αριθμός για μη μηδενικό α(α διάφορο του 0).
Δεν υπάρχει γενίκευση για όλους τους πραγματικούς α και n, όμως όταν η βάση α είναι θετικός πραγματικός αριθμός, το αn μπορεί να οριστεί για όλους τους πραγματικούς ή μιγαδικούς n μέσω της εκθετικής συνάρτησης ez. Οι τριγωνομετρικές συναρτήσεις μπορούν να εκφραστούν με όρους μιγαδικής δύναμης.
Η δύναμη όταν ο εκθέτης είναι μητρώο χρησιμοποιείται για την επίλυση συστημάτων γραμμικών διαφορικών εξισώσεων.
Η δύναμη έχει εφαρμογή και σε πολλά άλλα πεδία, όπως τα οικονομικά, η βιολογία, η χημεία, η φυσική και η επιστήμη υπολογιστών, με εφαρμογές στον ανατοκισμό, την πληθυσμιακή αύξηση, τη συμπεριφορά κυμάτων και την κρυπτογράφηση δημόσιου κλειδιού.

Ακέραιοι εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Η πράξη της δύναμης με ακέραιο εκθέτη απαιτεί στοιχειώδη άλγεβρα μόνο.
Θετικοί εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Η έκφραση α2 = α·α ονομάζεται τετράγωνο του α επειδή η επιφάνεια ενός τετραγώνου με πλευρά α ισούται με α2.
Η έκφραση α3 = α·α·α ονομάζεται κύβος, επειδή ο όγκος κύβου πλευράς α ισούται με α3.
Έτσι το 32 διαβάζεται «3 στο τετράγωνο» ή «τετράγωνο του 3» και το 23 διαβάζεται «2 στον κύβο» ή «κύβος του 2».
Ο εκθέτης ορίζει το πόσες φορές πολλαπλασιάζεται η βάση με τον εαυτό της. Για παράδειγμα, 35 = 3·3·3·3·3 = 243. Η βάση 3 εμφανίζεται 5 φορές στον επαναλαμβανόμενο (ή μεγάλο) πολλαπλασιασμό, επειδή ο εκθέτης είναι 5. Εδώ 3 είναι η βάση, 5 ο εκθέτης και 243 η δύναμη ή πιο συγκεκριμένα, η πέμπτη δύναμη του 3 ή το 3 στην πέμπτη. Έτσι το 35 διαβάζεται απλώς 3 στην πέμπτη.
Πιο επίσημα, οι δυνάμεις με θετικό εκθέτη μπορούν να οριστούν με την αρχική συνθήκη α1 = α και τη σχέση αn+1 = α·αn. Τότε ο λόγος ''Προσεταιριστική ιδιότητα/προσεταιριστική ιδιότητα'' του πολλαπλασιασμού, ισχύει για κάθε θετικούς m και n, αm+n = αm·αn .
Εκθέτες ένα και μηδέν[Επεξεργασία | επεξεργασία κώδικα]
Να σημειωθεί ότι το α1 είναι το «γινόμενο» ενός μόνο α, το οποίο ορίζεται να είναι α. Επίσης να σημειωθεί ότι αn − 1 = αn/α. Υποθέτοντας ότι n = 1, το αποτέλεσμα είναι α0 = 1. Ένας άλλος τρόπος να δειχθεί αυτό είναι όταν τα n, m, και n − m είναι θετικοί (και αν το α δεν είναι μηδέν), τότε φαίνεται ότι:
Επεκτείνοντας στην ειδική περίπτωση όπου n και m είναι ίσα, η εξίσωση γίνεται
καθώς και ο αριθμητής και ο παρονομαστής είναι ίσοι. Συνεπώς αυτό λαμβάνεται ως ο ορισμός του α0. Αυτό οδηγεί στον επόμενο κανόνα:
- Οποιοσδήποτε αριθμός υψωμένος στην δύναμη του 1 είναι ο ίδιος ο αριθμός
- Οποιοσδήποτε μη μηδενικός αριθμός υψώνεται στη δύναμη του 0 κάνει 1. Μία ερμηνεία αυτών των δυνάμεων είναι ως κενά γινόμενα. Η περίπτωση του 00 εξετάζεται παρακάτω.
Συνδυαστική ερμηνεία[Επεξεργασία | επεξεργασία κώδικα]
Για τους μη αρνητικούς ακεραίους n και m, η δύναμη nm ισούται με τον πληθικό αριθμό του συνόλου των m-άδων ενός συνόλου n στοιχείων, ή ο αριθμός των λέξεων m γραμμάτων ενός αλφαβήτου n γραμμάτων.
- 05 = | {} | = 0. Δεν υπάρχουν 5-άδες από ένα κενό σύνολο.
- 14 = | { (1,1,1,1) } | = 1. Υπάρχει μία 4-άδα από ένα σύνολο ενός στοιχείου.
- 23 = | { (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2) } | = 8. Υπάρχουν οκτώ 3-άδες από ένα σύνολο δύο στοιχείων.
- 32 = | { (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) } | = 9. Υπάρχουν εννιά 2-άδες από ένα σύνολο τριών στοιχείων.
- 41 = | { (1), (2), (3), (4) } | = 4. Υπάρχουν μία 4-άδες από ένα σύνολο τεσσάρων στοιχείων.
- 50 = | { () } | = 1. Υπάρχει ακριβώς μία κενή πλειάδα.
Δείτε επίσης ύψωση συνόλων σε δύναμη.
Αρνητικοί ακέραιοι εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Εξ ορισμού, η ύψωση ενός μη μηδενικού αριθμού στη δύναμη -1 παράγει τον αντίστροφό του:
Ορίζεται επίσης
για κάθε μη μηδενικό α και οποιονδήποτε θετικό ακέραιο n. Υψώνοντας το 0 σε αρνητική δύναμη συνεπάγεται διαίρεση με το μηδέν, έτσι δεν ορίζεται.
Ο ορισμός του α−n για μη μηδενικό α γίνεται έτσι ώστε η ταυτότητα αmαn = αm+n, που αρχικά ισχύει μόνο για μη αρνητικούς ακεραίους m και n, να ισχύει για οποιουσδήποτε ακεραίους m και n. Πιο συγκεκριμένα, αν τεθεί σε αυτή την ταυτότητα m = −n σημαίνει ότι
όπου α0 ορίζεται παραπάνω, πράγμα που υποκινεί τον ορισμό α−n = 1/αn που φαίνεται πιο πάνω.
Η ύψωση σε αρνητική ακέραια δύναμη μπορεί εναλλακτικά να ειδωθεί ως επαναλαμβανόμενη διαίρεση του 1 από τη βάση. Για παράδειγμα,
- .
Ταυτότητες και ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Η πιο σημαντική ταυτότητα που ικανοποιείται από την ύψωση σε ακέραια δύναμη, εφόσον η βάση δεν είναι μηδέν, είναι η εξής:
Αυτή η ταυτότητα έχει συνέπεια την
για α ≠ 0, και
Μία άλλη βασική ταυτότητα είναι
Ενώ η πρόσθεση και ο πολλαπλασιασμός είναι αντιμεταθετικές πράξεις (για παράδειγμα 2+3 = 5 = 3+2 και 2·3 = 6 = 3·2), η ύψωση σε δύναμη δεν είναι: 23 = 8, όμως 32 = 9.
Παρομοίως, ενώ η πρόσθεση και ο πολλαπλασιασμός είναι προσεταιριστικές πράξεις (για παράδειγμα (2+3)+4 = 9 = 2+(3+4) και (2·3)·4 = 24 = 2·(3·4), η ύψωση σε δύναμη δεν είναι: 23 στην 4η κάνει 84 ή 4096, όμως 2 στην 34 κάνει 281 ή 2.417.851.639.229.258.349.412.352. Όταν δεν υπάρχουν παρενθέσεις ώστε να τροποποιήσουν την ιεραρχία των υπολογισμών, η σειρά εκλαμβάνεται συνήθως από πάνω προς τα κάτω και όχι το ανάποδο:
Δυνάμεις του δέκα[Επεξεργασία | επεξεργασία κώδικα]
Στο δεκαδικό σύστημα, οι ακέραιες δυνάμεις του 10 γράφονται ως το ψηφίο 1 με ένα αριθμό μηδενικών να ακολουθούν ή να προηγούνται, ανάλογα με το μέγεθος και το πρόσημο του εκθέτη. Για παράδειγμα 103 = 1000 και 10−4 = 0.0001.
Η δυνάμεις του 10 χρησιμοποιούνται στον επιστημονικό συμβολισμό για να περιγράψουν μεγάλους ή μικρούς αριθμούς. Για παράδειγμα, 299,792,458 μέτρα/δευτερόλεπτο (η ταχύτητα του φωτός στο κενό) μπορεί να γραφτεί ως 2,99792458·108 m/s και εν συνεχεία κατά προσέγγιση ως 2,998·108 m/s
Τα προθέματα του SI βασίζονται σε δυνάμεις του 10 και χρησιμοποιούνται για να περιγράψουν μικρές ή μεγάλες ποσότητες. Για παράδειγμα το πρόθεμα k (Kilo- Κίλο) σημαίνει 103 = 1000, έτσι ένα KPa (κιλο-πασκάλ) ισούται με 1000 Pa (Πασκάλ).
Δυνάμεις του δύο[Επεξεργασία | επεξεργασία κώδικα]
Οι θετικές δυνάμεις του δύο είναι σημαντικές στην επιστήμη των υπολογιστών επειδή υπάρχουν 2n πιθανές τιμές σε μία δυαδική μεταβλητή n-bit.
Οι δυνάμεις του 2 είναι σημαντικές στη θεωρία συνόλων καθώς ένα σύνολο με n στοιχεία, έχει δυναμοσύνολο, ή σύνολο όλων των υποσυνόλων του με 2n στοιχεία.
Κοινή χρήση έχουν και οι αρνητικές δυνάμεις του 2.
Στο δυαδικό σύστημα, οι ακέραιες δυνάμεις του 2 γράφονται ως 1 με μηδενικά να προηγούνται ή να ακολουθούν αναλόγως με το πρόσημο και το μέγεθος του εκθέτη. Για παράδειγμα, το δύο στην τρίτη γράφεται ως 1000 στο δυαδικό.
Δυνάμεις του ένα[Επεξεργασία | επεξεργασία κώδικα]
Όλες οι ακέραιες δυνάμεις του ένα ισούνται με ένα: 1n = 1.
Δυνάμεις του μηδενός[Επεξεργασία | επεξεργασία κώδικα]
Αν ο εκθέτης είναι θετικός, η δύναμη του μηδενός είναι μηδέν: 0n = 0, όπου n > 0.
Αν ο εκθέτης είναι αρνητικός, η δύναμη του μηδενός (0n, όπου n < 0) δεν ορίζεται, καθώς εξ ορισμού συνεπάγεται διαίρεση με το μηδέν.
Αν ο εκθέτης είναι μηδέν, κάποιοι συγγραφείς ορίζουν 00=1, ενώ άλλοι το αφήνουν αόριστο, όπως αναλύεται παρακάτω
Δυνάμεις του μείον ένα[Επεξεργασία | επεξεργασία κώδικα]
Αν το n είναι άρτιος ακέραιος, τότε (−1)n = 1.
Άν το n είναι περιττός ακέραιος, τότε (−1)n = −1.
Εξαιτίας αυτής της ιδιότητας, οι δυνάμεις του -1 είναι χρήσιμες για την έκφραση εναλλασσόμενων ακολουθιών. Για παρόμοια ανάλυση των δυνάμεων του μιγαδικού αριθμού i, δείτε Δυνάμεις των μιγαδικών αριθμών.
Μεγάλοι εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Το όριο της ακολουθίας των δυνάμεων ενός αριθμού μεγαλύτερου του ένα αποκλίνει, με άλλα λόγια αυξάνονται χωρίς όριο:
- αn → ∞ καθώς n → ∞ όταν α > 1 .
Αυτό μπορεί να διαβαστεί ως «το α στην n τείνει στο +∞ (συν άπειρο) καθώς το n τείνει στο άπειρο όταν το α είναι μεγαλύτερο του ένα».
Οι δυνάμεις ενός αριθμού του οποίου η απόλυτη τιμή είναι μικρότερη από ένα τείνουν στο μηδέν:
- αn → 0 καθώς n → ∞ όταν |α| < 1 .
Οποιαδήποτε δύναμη του ένα είναι πάντα ένα:
- αn = 1 για όλα τα n αν α = 1 .
Αν ο αριθμός α ποικίλει τείνοντας στο 1 καθώς ο εκθέτης τείνει στο άπειρο τότε το όριο δεν είναι απαραίτητα ένα από τα παραπάνω. Μια ιδιαίτερα σημαντική περίπτωση είναι:
- (1+n−1)n → e καθώς n→∞
Δείτε την ενότητα παρακάτω Δυνάμεις του e.
Άλλα όρια, ιδιαίτερα αυτά που τείνουν σε απροσδιόριστες μορφές, περιγράφονται στο όρια των δυνάμεων παρακάτω.
Πραγματικές δυνάμεις θετικών αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Η ύψωση ενός θετικού πραγματικού σε δύναμη που δεν είναι ακέραιος μπορεί να γίνει με δύο τρόπους.
- Ρητοί εκθέτες μπορούν να οριστούν ως n-οστές ρίζες και από κει και πέρα όλοι οι εκθέτες μπορούν να οριστούν από την συνέχεια.
- Μπορεί να χρησιμοποιηθεί ο φυσικός λογάριθμος για τον ορισμό όλων των πραγματικών εκθετών με χρήση της εκθετικής συνάρτησης.
Οι ταυτότητες και ιδιότητες που δείχτηκαν παραπάνω για ακέραιους εκθέτες ισχύουν και για θετικούς πραγματικούς με μη ακέραιο εκθέτη. Ωστόσο η ταυτότητα
δεν μπορεί να γενικευθεί όταν το α είναι αρνητικός πραγματικός, δείτε αρνητικές νιοστές ρίζες. Η μη ισχύς αυτής της ταυτότητας είναι η πηγή των προβλημάτων με τις δυνάμεις των μιγαδικών αριθμών, όπως περιγράφεται και στην ενότητα μη ισχύς ταυτοτήτων δυνάμεων και λογαρίθμων.
Κύρια n-οστή ρίζα[Επεξεργασία | επεξεργασία κώδικα]
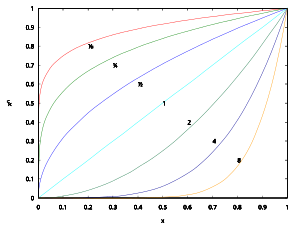
Η n-οστή ρίζα ενός αριθμού α είναι ένας αριθμός x τέτοιος ώστε xn = α
Αν α είναι θετικός πραγματικός και n είναι θετικός ακέραιος, τότε υπάρχει ακριβώς μία θετική πραγματική λύση της εξίσωσης xn = α. Αυτή η λύση αποκαλείται κύρια n-οστή ρίζα του α. Αυτό συμβολίζεται με n√α, όπου το σύμβολο √ είναι το ριζικό. Εναλλακτικά, μπορεί να γραφεί ως α1/n. Για παράδειγμα: 41/2 = 2, 81/3 = 2,
Όταν αναφέρεται η n-οστή ρίζα ενός θετικού πραγματικού α, συνήθως εννοείται η κύρια n-οστή ρίζα.
Ρητοί εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Η δύναμη ενός θετικού πραγματικού α με ρητό εκθέτη m/n (το m/n ανάγωγο) ικανοποιεί την σχέση
όπου m είναι ακέραιος και n είναι θετικός ακέραιος.
Δυνάμεις του e[Επεξεργασία | επεξεργασία κώδικα]
Η σημαντική μαθηματική σταθερά e, που αποκαλείται και αριθμός Euler, είναι περίπου ίση με 2,718 και είναι η βάση του φυσικού λογαρίθμου. Παρέχει ένα τρόπο ορισμού της ύψωσης σε δύναμη με μή ακέραιους εκθέτες. Ο αριθμός e ορίζεται ως:
Η εκθετική συνάρτηση ορίζεται ως:
ενώ το x γράφεται ως δύναμη καθώς ικανοποιεί την βασική εκθετική ταυτότητα
Η εκθετική συνάρτηση ορίζεται για όλες τις ακέραιες, κλασματικές, πραγματικές και μιγαδικές τιμές του x. Μπορεί ακόμα να οριστεί ώστε να επεκταθεί η ύψωση σε δύναμη και σε μη αριθμητικές οντότητες όπως τα τετραγωνικά μητρώα, ωστόσο η εκθετική ταυτότητα ισχύει μόνο όταν τα x και y αντιμετατίθενται.
Μία σύντομη απόδειξη ότι το e υψωμένο σε θετική ακέραια δύναμη k είναι το ίδιο με το ek είναι:
Αυτή η απόδειξη δείχνει επίσης ότι η έκφραση ex+y ικανοποιεί την εκθετική ταυτότητα όταν τα x και y είναι θετικοί ακέραιοι. Αυτά τα αποτελέσματα είναι εν γένει αληθή για όλους τους αριθμούς και όχι μόνο για θετικούς ακέραιους.
Πραγματικοί εκθέτες[Επεξεργασία | επεξεργασία κώδικα]
Καθώς οποιοσδήποτε πραγματικός αριθμός μπορεί να προσεγγιστεί από ρητούς αριθμούς, η ύψωση σε έναν τυχαίο πραγματικό x μπορεί να οριστεί μέσω συνέχειας ως
όπου το όριο καθώς το r τείνει στο x λαμβάνεται μόνο από τις ρητές τιμές του r.
Για παράδειγμα αν
τότε
Η ύψωση σε πραγματική δύναμη κανονικά υπολογίζεται με την χρήση λογαρίθμων αντί για την χρήση ορίων και ρητών δυνάμεων.
Ο φυσικός λογάριθμος ln(x) είναι η αντίστροφη της εκθετικής συνάρτησης ex. Ορίζεται για b > 0 και ικανοποιεί την
Αν bx ικανοποιεί τους περιορισμούς του λογαρίθμου και του εκθέτη, τότε πρέπει
για κάθε πραγματικό x.
Αυτό μπορεί να χρησιμοποιηθεί ως εναλλακτικός ορισμός της πραγματικής δύναμης bx και συμφωνεί με τον ορισμό που δόθηκε παραπάνω κάνοντας χρήση ρητών εκθετών και της συνέχειας. Ο ορισμός με χρήση λογαρίθμων είναι πιο κοινός στα πλαίσια των μιγαδικών αριθμών όπως αναλύεται παρακάτω.
Αρνητικές n-οστές ρίζες[Επεξεργασία | επεξεργασία κώδικα]
Οι δυνάμεις ενός θετικού πραγματικού είναι πάντα θετικοί πραγματικοί αριθμοί. Η λύση της x2 = 4 μπορεί ωστόσο να είναι είτε 2 είτε -2. Η κύρια τιμή του 41/2, όμως το -2 είναι επίσης έγκυρη τετραγωνική ρίζα. Αν ο ορισμός της ύψωσης σε δύναμη των πραγματικών αριθμών επεκταθεί ώστε να επιτρέπονται και αρνητικά αποτελέσματα τότε το αποτέλεσμα δεν συμπεριφέρεται πλέον καλά.
Αν το n είναι άρτιος τότε η xn = α έχει δύο λύσεις αν το α είναι θετικό, οι οποίες είναι η θετική και η αρνητική n-οστή ρίζα. Η εξίσωση δεν έχει πραγματική λύση αν το α είναι αρνητικό.
Αν το n είναι περιττός, τότε η xn = α έχει μία πραγματική λύση. Η λύση είναι θετική αν το α είναι θετικός και αρνητική αν το α είναι αρνητικός.
Η ρητή δύναμη m/n, όπου m/n ανάγωγο, είναι θετική αν το m είναι άρτιος, αρνητική αν το α είναι αρνητικός και τα m και n είναι περιττοί, και μπορεί να είναι είτε θετική είτε αρνητική αν ο α είναι θετικός και το n περιττός. (−27)1/3 = −3, (−27)2/3 = 9, ενώ το 43/2 έχει δύο ρίζες, το 8 και το -8. Καθώς δεν υπάρχει πραγματικός αριθμός x ώστε x2 = −1, ο ορισμός του αm/n όταν το α είναι αρνητικός και το n άρτιος πρέπει να κάνει χρήση της φανταστικής μονάδας i, όπως περιγράφεται αναλυτικότερα στην ενότητα Δυνάμεις των μιγαδικών αριθμών.
Ούτε με η μέθοδος του λογάριθμου όυτε η μέθοδος του ρητού εκθέτη μπορεί να χρησιμοποιηθεί για να οριστεί το αr για αρνητικό πραγματικό α και οποιονδήποτε πραγματικό r. Η er είναι θετική για κάθε πραγματικό r και έτσι το ln(α) δεν ορίζεται στους πραγματικούς για α ≤ 0. (Από την άλλη, μπορεί οριστεί οποιαδήποτε μιγαδική δύναμη ενός αρνητικού αριθμού α επιλέγοντας έναν μιγαδικό λογάριθμο του α.)
Η μέθοδος του ρητού εκθέτη δεν μπορεί να χρησιμοποιηθεί για αρνητικές δυνάμεις του α επειδή βασίζεται την συνέχεια. Η συνάρτηση f(r) = αr έχει μοναδική συνεχή επέκταση από τους ρητούς αριθμούς στους πραγματικούς για κάθε α > 0. Όταν όμως α < 0, η συνάρτηση f δεν είναι καν συνεχής στο σύνολο των ρητών αριθμών στο οποίο ορίζεται.
Για παράδειγμα, έστω α = −1. Η n-οστή ρίζα του -1 είναι -1 για κάθε περιττό φυσικό αριθμό n. Έτσι αν το n είναι περιττός θετικός ακέραιος (−1)(m/n) = −1 αν το m είναι περιττός, και (−1)(m/n) = 1 αν το m είναι άρτιος. Έτσι το σύνολο των ρητών αριθμών q για το οποίο (−1)q = 1 είναι πυκνό στους ρητούς αριθμός, όπως είναι και το σύνολο των q για τους οποίους (−1)q = −1. Αυτό σημαίνει ότι η συνάρτηση (−1)q δεν είναι συνεχής για οποιονδήποτε ρητό q.
Προσοχή χρειάζεται όταν εφαρμόζονται οι ταυτότητες των δυνάμεων με αρνητικές n-οστές ρίζες. Για παράδειγμα, −27 = (−27)((2/3)×(3/2)) = ((−27)2/3)3/2 = 93/2 = 27 είναι προφανώς λάθος. Το πρόβλημα προκύπτει επειδή λαμβάνεται η θετική τετραγωνική ρίζα αντί για την αρνητική στο τελευταίο βήμα, όμως εν γένει προκύπτουν τα ίδια προβλήματα με αυτά που περιγράφονται για τους μιγαδικούς στην ενότητα Μη ισχύς των εκθετικών και λογαριθμικών ταυτοτήτων
Μιγαδικές δυνάμεις θετικών πραγματικών αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Φανταστικές δυνάμεις e[Επεξεργασία | επεξεργασία κώδικα]

Η γεωμετρική ερμηνεία των πράξεων με μιγαδικούς αριθμούς και ο ορισμός των δυνάμεων του e είναι το στοιχείο για την κατανόηση του eix για πραγματικούς x. Έστω το ορθογώνιο τρίγωνο (0, 1, 1 + ix/n). Για μεγάλες τιμές του n το τρίγωνο είναι σχεδόν κυκλικός τομέας με μικρή κεντρική γωνία ίση με x/n ακτίνια. Τα τρίγωνα (0, (1 + ix/n)k, (1 + ix/n)k+1) είναι όμοια για κάθε k. Έτσι για μεγάλες τιμές του n το όριο του (1 + ix/n) είναι το σημείο στον μοναδιαίο κύκλο του οποίου η γωνία από τον θετικό πραγματικό άξονα είναι x ακτίνια. Οι πολικές συντεταγμένες αυτού του σημείου είναι (r, θ) = (1, x), και οι καρτεσιανές (cos x, sin x). Έτσι e ix = cos x + isin x, και αυτή είναι ο τύπος του Euler που συνδέει την άλγεβρα και την τριγωνομετρία μέσω των μιγαδικών αριθμών.
Η λύσεις της εξίσωσης ez = 1 είναι τα ακέραια πολλαπλάσια του 2πi:
Πιο γενικά, αν if eb = α, τότε κάθε λύση του ez = α μπορεί να βρεθεί προσθέτονταν ένα ακέραιο πολλαπλάσιο του 2πi στο b:
Έτσι η μιγαδική εκθετική συνάρτηση είναι περιοδική συνάρτηση με περίοδο 2πi.
Πιο απλά: eiπ = −1; ex + iy = ex(cos y + i sin y).
Τριγωνομετρικές συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
Από τον τύπο του Euler προκύπτει ότι οι τριγωνομετρικές συναρτήσεις συνημίτονο και ημίτονο είναι
Ιστορικά, το συνημίτονο και το ημίτονο ορίζονταν γεωμετρικά πριν την εφεύρεση των μιγαδικών αριθμών. Η παραπάνω εξίσωση απλοποιεί τις πολύπλοκες εξισώσεις τριγωνομετρικών συναρτήσεων αθρίσματος σε απλή εξίσωση ύψωσης σε δύναμη.
Μιγαδικές δυνάμεις του e[Επεξεργασία | επεξεργασία κώδικα]
Η δύναμη z = ex+i·y μπορεί να υπολογιστεί ως ex · ei·y. Ο πραγματικός παράγοντας ex είναι η απόλυτη τιμή του z και ο μιγαδικός παράγοντας ei·y προσδιορίζει την κατεύθυνση του z.
Μιγαδικές δυνάμεις των θετικών πραγματικών αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Αν α είναι θετικός ακέραιος, και z τυχαίος μιγαδικός, η δύναμη αz ορίζεται ώς ez·ln(α), όπου x = ln(α) είναι η μοναδική πραγματική λύση της εξίσωσης ex = α. Έτσι η ίδια μέθοδος που ισχύει για πραγματικούς εκθέτες ισχύει και για μιγαδικούς. Για παράδειγμα:
- 2i = e i·ln(2) = cos(ln(2)) + i·sin(ln(2)) ≈ 0.76924 + 0.63896i
- ei ≈ 0.54030 + 0.84147i
- 10i ≈ −0.66820 + 0.74398i
- (e2π)i ≈ 535.49i ≈ 1
Δυνάμεις μιγαδικών αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Οι ακέραιες δυνάμειες μή μηδενικών μιγαδικών αριθμών ορίζονται με επαναλαμβανόμενο πολλαπλασιασμό όπως παραπάνω. Αν i είναι η φανταστική μονάδα και n είναι ακέραιος, τότε in ισούται με 1, i, -1 ή -i, αναλόγως με το αν ο ακέραιος n είναι ίσος με 0, 1, 2, ή 3 modulo 4. Εξαιτίας αυτού, οι δυνάμεις του i είναι χρήσιμες στην έκφραση ακολουθιών με περίδο 4.
Οι μιγαδικές δυνάμεις θετικών πραγματικών ορίζονται μέσω του ex όπως στην ενότητα Μιγαδικές δυνάμεις θετικών πραγματικών αριθμών παραπάνω. Αυτές είναι συνεχείς συναρτήσεις.
Η γενίκευση αυτών των συναρτήσεων στην περίπτωση των μη ακέραιων δυνάμεων μιγαδικών αριθμών οδηγεί σε δυσκολίες. Είτε πρέπει να οριστούν ως ασυνεχείς συναρτήσεις είτε ως πλειότιμες συναρτήσεις. Καμία από τις δύο επιλογές δεν είναι εντελώς ικανοποιητική.
Η ρητή δύναμη ενός μιγαδικού αριθμού πρέπει να είναι η λύση μιας αλγεβρικής εξίσωσης. Συνεπώς πάντα έχει πεπερασμένο αριθμό πιθανών τιμών. Για παράδειγμα το w = z1/2 πρέπει να είναι λύση της εξίσωσης w2 = z. αν όμως το w είναι λύση θα πρέπει να είναι και το -w, επειδή (−1)2 = 1. Μπορεί να επιλεγεί αυθαίρετα μία μοναδική λύση η οποία αποκαλείται κύρια τιμή με βάση ένα γενικό κανόνα που ισχύει και για τις άρρητες δυνάμεις.
Οι μιγαδικές δυνάμεις και λογάριθμοι διαχειρίζονται με πιο φυσικό τρόπο αν εκληφθούν ως μονότιμες συναρτήσεις σε μία επιφάνειες Ρίμαν. Οι μονότιμες εκδοχές ορίζονται από την επιλογή φύλλου. Η τιμή έχει ασυνέχεια κατά μήκος της τομής διακλαδώσεως. Επιλέγοντας μία από τις πολλές λύσεις ως κύρια τιμή, οι συναρτήσεις παραμένου ασυνεχείς και οι συνήθεις κανόνες για τον χειρισμό των δυνάμεων μπορεί να οδηγίσουν σε σφάλμα.
Οποιαδήποτε μη ρητή δύναμη ενός μιγαδικού αριθμού έχει άπειρο αριθμό πιθανών τιμών εξαιτίας της πλειότιμης φύσης του μιγαδικού λογάριθμου (δείτε παρακάτω). Η κύρια τιμή είναι μία μοναδική τιμή που επιλέγεται από αυτές με βάση ένα κανόνα ο οποίος, ανάμεσα στις άλλες ιδιότητές του, διασφαλίζει ότι οι δυνάμεις μιγαδικών αριθμών με θετικό πραγματικό μέρος και μηδενικό φανταστικό μέρος δίνουν την ίδια τιμή με την αντίστοιχη δύναμη πραγματικού αριθμού.
Η ύψωση σε μιγαδική δύναμη ενός πραγματικού είναι τυπικά διαφορετική πράξη από την ανάλογη για μιγαδικό αριθμό. Ωστόσο στην κοινή περίπτωση του θετικού πραγματικού αριθμού η κύρια τιμή είναι η ίδια.
Οι δυνάμεις αρνητικών πραγματικών αριθμών δεν ορίζονται πάντα και είναι ασυνεχείς ακόμα και όταν ορίζονται. Όταν εμπλεκονται μιγαδικοί αριθμού συνήθως χρησιμοποιείται η πράξη των μιγαδικών.
Μιγαδικές δυνάμεις μιγαδικού αριθμού[Επεξεργασία | επεξεργασία κώδικα]
Για μιγαδικούς αριθμούς α και b με α ≠ 0, ο συμβολισμός αb είναι αμφίσημος κατά την ίδια έννοια που είναι και ο log α.
Για να υπολογιστεί η τιμή αb, πρώτα πρέπει να επιλεγεί ένας λογάριθμος του α, έστω log α. Η επιλογή μπορεί να είναι η κύρια τιμή Log α (το προκαθορισμένο, αν δεν δίνεται άλλη διευκρίνηση), ή πιθανώς μια τιμή που δίνεται από κάποιον άλλο κλάδο του log z προκαθορισμένο εκ των προτέρων. Επειτα χρησιμοποιώντας την μιγαδική εκθετική συνάρτηση ορίζεται:
Επειδή αυτό συμφωνεί με τον προηγούμενο ορισμό στην περίπτωση όπου α είναι θετικός πραγματικός αριθμός και χρησιμοποείται η κύρια τιμή του log α.
Αν το b είναι ακέραιος, τότε η τιμή του αb είναι ανεξάρτητη από την επιλογή του log α, και συμφωνεί με τον προηγούμενο ορισμό για ακέραιο εκθέτη.
Αν το b είναι ρητός αριθμός n/m (n, m πρώτοι μεταξύ τους και m > 0) τότε οι άπειρες επιλογές για log α αποδίδουν μόνο m διαφορετικές τιμές για το αb. Αυτές οι τιμές είναι οι m μιγαδικές λύσεις z της εξίσωσης zm = αn.
Αν b είναι άρρητος αριθμός, τότε οι άπειρες επιλογές για το log α οδηγούν σε άπειρες διακριτές τιμές για το αb.
Ο υπολογισμός των μιγαδικών δυνάμεων γίνεται μετατρέποντας την βάση α σε πολική μορφή, όπως περιγράφεται αναλυτικά παρακάτω.
Παρόμοια δομή εφαρμόζεται και στις τετράδες (Quaternions).
Μιγαδικές ρίζες της μονάδας[Επεξεργασία | επεξεργασία κώδικα]

Ένας μιγαδικός αριθμός α τέτοιος ώστε αn = 1 για θετικό ακέραιο n ονομάζεται n-οστή ρίζα της μονάδος. Γεωμετρικά, οι n-οστές ρίζες της μονάδας κείτονται σε μοναδιαίο κύκλο στο μιγαδικό επίπεδο στης κορυφές ενός κανονικού n-γώνου με την μία κορυφή να είναι στον πραγματικό αριθμό 1.
Αν zn = 1 όμως zk ≠ 1 για όλους τους φυσικούς αριθμούς k τέτοιους ώστε 0 < k < n, τότε το z καλείται αρχική ρίζα της μονάδος. Η αρνητική μονάδα -1 είναι η μοναδική αρχική τετραγωνική ρίζα της μονάδας. Η φανταστική μονάδα i είναι μία από τις δύο αρχικές 4ες ρίζες της μονάδος, η άλλη είναι το -i.
Ο αριθμός e2πi (1/n) είναι η αρχική n-οστή ρίζα της μονάδος με το μικρότερο θετικό όρισμα. (Κάποιες φορές αποκαλείται και κύρια n-οστή ρίζα της μονάδας, αλλά δεν είναι καθολική ορολογία και δεν θα πρέπει να συγχέεται με την κύρια τιμή της √1 η οποια είναι 1.[1])
Οι άλλες n-οστές ρίζες της μονάδας δίδονται από τη σχέση
για 2 ≤ k ≤ n.
Ρίζες τυχαίων μιγαδικών αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Αν και υπάρχουν άπειρες πιθανές τιμές για ένα γενικό μιγαδικό αλγόριθμο, υπάρχει πεπερασμένος αριθμός τιμών για τη δύναμη az στην σημαντική ειδική περίπτωση όπου z = 1/n και n είναι θετικός ακέραιος. Αυτές είναι οι n-οστές ρίζες του α, είναι οι λύσεις της εξίσωσης xn = α. Όπως και με τις πραγματικές ρίζες, η δεύτερη ρίζα ονομάζεται τετραγωνική, και η τρίτη, κυβική ρίζα.
Είναι βολικό να ορίζεται η α1/n ως η κύρια τιμή της ρίζας. Αν α είναι θετικός πραγματικός αριθμός, είναι βολικό επίσης να επιλεγεί ένας θετικός πραγματικός ως η κύρια τιμή της ρίζας α1/n. Για μιγαδικούς αριθμούς εν γένει επιλέγεται η n-οστή ρίζα με το μικρότερο όρισμα ως κύρια τιμή, όπως και με τις κύριες τιμές των ριζών της μονάδας.
Το σύνολο των n-στών ριζών ενός μιγαδικού α υπολογίζεται πολαπλασιάζονταν την κύρια τιμή α1/n με κάθε μία από τις n-οστές ρίζες της μονάδος. Για παράδειγμα, οι τέταρτες ρίζες του 16 είναι 2, -2, 2i, και -2i, επειδή η κύρια τιμή της τέταρτης ρίζας του 16 είναι 2 και οι τέταρτες ρίζες της μονάδος είναι 1, −1, i, και −i.
Υπολογισμός μιγαδικών δυνάμεων[Επεξεργασία | επεξεργασία κώδικα]
Είναι συχνά ευκολότερο να υπολογιστούν μιγαδικές δυνάμεις γράφοντας τον αριθμό σε πολική μορφή. Κάθε μιγαδικός αριθμός z μπορεί να γραφτεί στην πολική μορφή
Όπου r είναι μη αρνητικός πραγματικός και θ είναι το όρισμα του z. Η πολική μορφή έχει απλή γεωμετρική ερμηνεία: αν ένας μιγαδικός αριθμός u + iv εκληφθεί ότι αναπαριστά το σημείο (u, v) στο μιγαδικό επίπεδο χρησιμοποιώντας τις καρτεσιανές συντεταγμένες, τότε (r, θ) είναι το ίδιο σημείο σε πολικές συντεταγμένες. Δηλαδή r είναι η ακτίνα (radius) r2 = u2 + v2 και θ είναι η γωνία θ = atan2(v, u). Η πολική γωνία θ είναι δεν έχει συγκεκριμένη τιμή καθώς οποιοδήποτε πολλαπλάσιου του 2π και να προστεθεί σε αυτή δεν αλλάζει η θέση του σημείου. Κάθε επιλογή γωνίας θ δίνει εν γένει μια διαφορετική πιθανή τιμή για την δύναμη. Μία τομή διακλαδώσεως μπορεί να χρησιμοποιηθεί για να επιλεχθεί μία συγκεκριμένη τιμή. Η κύρια τιμή (η πιο κοινή τομή διακλαδώσεως), αντιστοιχεί σε θ στο διάστημα (−π, π]. Για μιγαδικούς αριθμούς με θετικό πραγματικό μέρος και μηδενικό φανταστικό μέρος, η χρήση της κύριας τιμής δίνει το ίδιο αποτέλεσμα με τον αντίστοιχο πραγματικό αριθμό.
Προκειμένου να υπολογιστεί η μιγαδική δύναμη αb, γράφεται το α σε πολική μορφή:
- .
τότε
και συνεπως
Αν το b αναλυθεί ως c + di, τότε ο τύπος για το αb μπορεί να γραφτεί πιο ρητά ως
Αυτός ο τελικός τύπος επιτρέπει τον εύκολο υπολογισμό των μιγαδικών δυνάμεων από αναλύσεις της βάσης σε πολική μορφή και του εκθέτη σε καρτεσιανή μορφή. Φαίνεται εδώ και σε πολική και σε καρτεσιανή μορφή (μέσω της ταυτότητας Euler).
Τα ακόλουθα παραδείγματα κάνουν χρήση της κύριας τιμής, της τομής διακλάδωσης ώστε το θ να είναι στο διάστημα (−π, π]. Για να υπολογιστεί το ii, γράφεται το i σε πολική και καρτεσιανή μορφή:
Τότε με τον παραπάνω τύπο, για r = 1, θ = π/2, c = 0, και d = 1, προκύπτει:
Παρομοίως βρίσκεται το (−2)3 + 4i, υπολογίζεται πρώτα η πολική μορφή του -2,
και γίνεται χρήση του παραπάνω τύπου ώστε να υπολογιστεί το
Η τιμή μίας μιγαδικής δύναμης εξαρτάται από τον κλάδο που χρησιμοποιείται. Για παράδειγμα, αν η πολική μορφή i = 1ei(5π/2) χρησιμοποιηθεί για τον υπολογισμό του i i, η δύναμη υπολογίζεται e−5π/2, η κύρια τιμή του i i, που υπολογίστηκε παραπάνω, είναι e−π/2. Το σύνολο όλων των πιθανών τιμών του i i δίνεται από:[2]
Συνεπώς υπάρχουν άπειρες τιμές που είναι πιθανές τιμές του i i, μία για κάθε ακέραιο k. Όλες έχουν μηδενικό φανταστικό μέρος, έτσι μπορεί να ειπωθεί ότι το i i έχει άπειρες έγκυρες πραγματικές τιμές.
Μη ισχύς των εκθετικών και λογαριθμικών ταυτοτήτων[Επεξεργασία | επεξεργασία κώδικα]
Κάποιες ταυτότες για δυνάμεις και λογαρίθμους που ισχύουν για τους πραγματικούς αριθμούς δεν ισχύουν για τους μιγαδικούς, ανεξαρτήτως του πως θα οριστεί η μιγαδική δύναμη και ο μιγαδικός λογάριθμος. Για παράδειγμα:
- Η ταυτότητα log(αb) = b · log α ισχύει όταν ο α είναι θετικός πραγματικός αριθμός και ο b είναι πραγματικός. Όμως στον κύριο κλάδο των μιγαδικών λογαρίθμων ισχύει π.χ.
- Ανεξαρτήτως του ποιος κλάδος λογαρίθμων θα χρησιμοποιηθεί, θα εμφανίζονται παρόμοιες ανωμαλίες. Το καλύτερο που μπορεί να γίνει (αν χρησιμοποιηθεί αυτό το αποτέλεσμα) είναι:
- Αυυή η ταυτότητα δεν ισχύει ούτε όταν ο λογάριθμος εκλαμβάνεται ως πλειότιμη συνάρτηση. Οι πιθανές τιμές του log(αb) περιέχουν τις τιμές του b · log α ως υποσύνολο. Χρησιμοποιώντας το συμβολισμό Log(α) για την κύρια τιμή του log(α) και m, n ως δύο τυχαίους ακέραιους οι πιθανές τιμές και των δύο μερών είναι:
- Οι ταυτότητες (ab)c = αcbc και(α/b)c = αc/bc είναι έγκυρες όταν α και b είναι θετικοί πραγματικοί αριθμοί και c είναι πραγματικός αριθμός. Όμως ο υπολογισμός χρησιμοποιώντας τον κύριο κλάδο δείχνει ότι
- και
- Από την άλλη, όταν c είναι ακέραιος, οι ταυτότητες είναι έγκυρες για όλους του μη μηδενικούς μιγαδικούς.
- Αν η ύψωση σε δύναμη θεωρηθεί πλειότιμη συνάρτηση τότε οι πιθανές τιμές του (−1×−1)1/2 είναι {1, −1}. Η ταυτότητα ισχύει, λέγοντας όμως ότι {1} = {(−1×−1)1/2} είναι λάθος.
- Η ταυτότητα (eα)b = eab ισχύει για πραγματικούς αριθμου΄ς α και b, όμως υποθέτωντας ότι ισχύει και για μιγαδικούς οδηγεί στο ακόλουθο παράδοξο, που ανακαλύφθηκε το 1827 από τον Clausen:[3]
- για οποιονδήποτε ακέραιο n, προκύπτει:
- που όμως είναι ψευδές όταν ο ακέραιος n είναι μη μηδενικός.
- Υπάρχουν κάποια προβλήματα στον συλλογισμό:
- Το κύριο σφάλμα είναι ότι αλλάζοντας την σειρά της ύψωσης σε δύναμη πηγαίνοντας από την γραμμή δύο στην τρία αλλάζει και η επιλογή της κύριας τιμής.
- Από την οπτική γωνία της πλειότιμης συνάρτησης το πρώτο σφάλμα εμφανίζεται πιο νωρίς, υποννοείται στην πρώτη γραμμή και δεν είναι εμφανές. Είναι το ότι το e είναι πραγματικός αριθμός ενώ το αποτέλεσμα e1+2πin είναι μιγαδικός αριθμός που αναπαριστάται καλύτερα ως e+0i. Αντικαθιστώντας την μιγαδική δύναμη με πραγματική στη δεύτερη γραμμή κάνει την δύναμη να έχει πολλές πιθανές τιμές. Αλλάζοντας τη σειρά με την οποία γίνεται η ύψωση σε δύναμη από τη γραμμή δύο στην τρία επίσης επιρεάζει το πόσες πιθανές τιμές μπορεί να έχει το αποτέλεσμα.
- για οποιονδήποτε ακέραιο n, προκύπτει:
Μηδέν στη μηδενική δύναμη[Επεξεργασία | επεξεργασία κώδικα]

Οι περισσότεροι συγγραφείς συμφωνούν με τα παρακάτω που σχετίζονται με το 00, παίρνουν όμως διαφορετικές αποφάσεις όταν πρόκειται να ορίσουν το 00 ή όχι: δείτε την επόμενη υποενότητα.
Στις περισσότερες περιπτώσεις που δεν έχουν να κάνουν με την συνέχεια στον εκθέτη, ερμηνεύοντας το 00 ως 1 απλοποιεί τους τύπους και μηδενίζει την ανάγκη για ειδικές περιπτώσεις στα θεωρήματα. (Δείτε την επόμενη παράγραφο για περιπτώσεις που έχουν να κάνουν με συνέχεια.)
Για παράδειγμα:
- Θεωρώντας το α0 ως κενό γινόμενο του εποδίδεται η τιμή 1, ακόμα και όταν α=0.
- Η συνδυαστική ερμηνεία του 00 είναι ο αριθμός των κενών πλειάδων στοιχείων από το κενό σύνολο. Υπάρχει μία ακριβώς κενή πλειάδα.
- Ισοδύναμα, το 00 ερμηνεύεται στο πλαίσιο των συνόλων ως ο αριθμός των συναρτήσεων από το κενό σύνολο προς το κενό σύνολο. Υπάρχει ακριβώς μία τέτοια συνάρτηση, η κενή συνάρτηση.[4]
- Ο συμβολισμός για τα πολυώνυμα και τις δυναμοσειρές βασίζεται στον ορισμό 00 = 1. Ταυτότητες όπως η και καθώς και το διωνυμικό θεώρημα δεν ισχύουν για x = 0 εκτός και άν00 = 1.[5]
- Στον διαφορικό λογισμό, ο ο κανόνας δεν είναι έγκυρος για n = 1 στο x = 0 αν δεν ισχύει 00 = 1.
Από την άλλη, όταν το 00 προκύπτει από όριο της μορφής , πρέπει να εκλαμβάνεται ως απροσδιόριστη μορφή.
- Τα όρια που περιλαμβάνουν αλγεβρικούς υπολογισμούς πρέπει να αποτιμούνται με την αντικατάσταση υποεκφράσεων από τα όριά τους, αν η έκφραση που προκύπτει δεν προσδιορίζει το αρχικό όριο, η έκφραση είναι γνωστή ως απροσδιόριστη μορφή.[6] Στην πραγματικότητα, όταν f(t) και g(t) είναι συναρτήσεις με πραγματικές τιμές που και οι δύο προσεγγίζουν το 0 (καθώς το t τείνει σε ένα πραγματικό αριθμό ή το ±∞), με f(t) > 0, η συνάρτηση f(t)g(t) δεν είναι αναγκαίο να τείνει στο 1. Αναλόγως με τις f και g, το όριο f(t)g(t) μπορεί να είναι οποιοσδήποτε μη αρνητικός αριθμός ή το +∞, ή μπορεί να είναι απροσδιόριστο. Για παράδειγμα, t → 0+ όμως τα όρια είναι διαφορετικά:
- .
- Έτσι το 00 είναι απροσδιόριστη μορφή. Αυτή η συμπεριφορά δείχνει ότι οι συνάρτηση δύο μεταβλητών xy, αν και συνεχής στο σύνολο {(x,y): x > 0}, δεν μπορεί να γενικευτεί σε συνεχή συνάρτηση σε οποιοδήποτε σύνολο περιέχει το (0,0), ανεξαρτήτως του πως ορίζεται το 00.[7] Ωστόσο υπό συνθήκες, όπως αν αμφότερες οι f και g είναι αναλυτικές συναρτήσεις και η f είναι μη αρνητική, το όριο από τα δεξιά είναι πάντα 1.[8][9][10]
- Στους μιγαδικούς αριθμούς, η συνάρτηση zw ορίζεται για μη μηδενικό z επιλέγοντας ένα κλάδο του log z και θέτοντας zw := ew log z, αλλά δεν υπάρχει κλάδος του log z που να ορίζεται στο z = 0, πόσο μάλλον σε μία γειτονιά του 0.[11]
Ιστορία των απόψεων πάνω στο 00[Επεξεργασία | επεξεργασία κώδικα]
Διαφορετικοί συγγραφείς ερμηνεύουν την κατάσταση που περιγράφηκε παραπάνω με διαφορετικό τρόπο:
- Κάποιοι ισχυρίζονται ότι η καλύτερη τιμή για το 00 εξαρτάται από τα συμφραζόμενα, και έτσι ο ορισμός του για όλα είναι προβληματικός.[12] Σύμφωνα με τον Μπένσον (Benson 1999), «η επιλογή για το άν θα οριστεί το 00 εξαρτάται από το πόσο βολικό είναι και όχι από το πόσο σωστό είναι.»[13]
- Άλλοι ισχυρίζονται ότι το 00 είναι 1. Σύμφωνα με την σ.408 του Knuth (1992), «πρέπει να είναι 1», αν και συνεχίζει λέγοντας ότι ο «Cauchy είχε καλούς λόγους ώστε να θεωρεί το 00 ως απροσδιόριστη οριακή μορφή» και ότι «υπό αυτή την πιο έντονη έννοια, η τιμή του 00 είναι λιγότερο ορισμένη από, έστω, την τιμή του 0+0» (η έμφαση του πρωτότυπου).[14]
Η διαμάχη συνεχίζεται τουλάχιστον από τις αρχές του 19ου αιώνα. Εκείνη την εποχή, οι περισσότεροι μαθηματικοί συμφωνούσαν ότι 00 = 1, μέχρι που το 1821 ο Cauchy[15] καταχώρισε το 00 μαζί με εκφράσεις όπως το στο πίνακα με τις απροσδιόριστες μορφές. Την δεκαετία του 1830 ο Libri[16][17] δημοσίευσε ένα μη πειστικό επιχείρημα υπέρ του 00 = 1, και ο Möbius[18] πήρε το μέρος του, ισχυριζόμενος ότι οποτεδήποτε Ένας σχολιαστής που υπέγραψε απλά ως «S» παρείχε το αντιπαράδειγμα του (e−1/t)t, γεγονός που σίγασε την διαμάχη για ένα διάστημα, με την κατάληξη ότι το 00 θα έπρεπε να είναι αόριστο.[14]
Χειρισμός από τους υπολογιστές[Επεξεργασία | επεξεργασία κώδικα]
Πρότυπο κινητής υποδιαστολής του IEEE[Επεξεργασία | επεξεργασία κώδικα]
Το πρότυπο κινητής υποδιαστολής IEEE 754-2008 χρησιμοποιείται για τον σχεδιασμό των περισσοτέρων βιβλιοθηκών κινητής υποδιαστολής. Προτείνει ένα αριθμό διαφορετικών συναρτήσεων για τον υπολογισμό μίας δύναμης:[19]
- Η pow χειρίζεται το 00 ως 1. Αυτή είναι η παλαιότερα ορισμένη έκδοση. Αν η δύναμη είναι ακέραιος τότο το αποτέλεσμα είναι το ίδιο με την powr (εκτός από κάποιες εξαιρετικές περιπτώσεις).
- Η pown χειρίζεται το 00 ως 1. Η δύναμη πρέπει να είναι ακέραιος. Η τιμή ορίζεται για αρνητικές βάσεις, π.χ. pown(−3,5) βγάζει −243.
- Η powr χειρίζεται το 00 ως NaN (Not-a-Number - όχι αριθμός, αόριστο). Η τιμή είναι επίσης NaN για περιπτώσεις όπως powr(-3,2) όπου η βάση είναι μικρότερη του μηδενός. Η τιμή ορίζεται ως epower×log(base).
Γλώσσες προγραμματισμού[Επεξεργασία | επεξεργασία κώδικα]
Οι περισσότερες γλώσσες προγραμματισμού με συνάρτηση δύναμης υλοποιούνται χρησιμοποιώντας την συνάρτηση pow του IEEE και συνεπώς αποτιμούν το 00 ως 1. Τα μεταγενέστερα πρότυπα της C[20] και της C++ περιγράφουν αυτή τη συμπεριφορά ως μη κανονική. Η μέθοδος System.Math.Pow του .NET Framework επείσης χειρίζεται το 00 ως 1.[21]
Όρια των δυνάμεων[Επεξεργασία | επεξεργασία κώδικα]
Στην ενότητα μηδέν στη μηδενική δύναμη υπάρχουν κάποια παραδείγματα ορίων τα οποία είναι της απροσδιόριστης μορφής 00. Τα όρια σε αυτά τα παραδείγματα υπάρχουν, αλλά έχουν διαφορετικές τιμές, δείχνοντας ότι η συνάρτηση δύο μεταβλητών xy δεν έχει όριο στο σημείο (0,0). Το ζήτημα είναι σε ποια σημεία έχει όριο αυτή η συνάρτηση.
Πιο συγκεκριμένα, έστω η συνάρτηση f(x,y) = xy, ορισμένη στο D = {(x,y) ∈ R2 : x > 0}. Τότε το D μπορεί να ειδωθεί ως υποσύνολο του R2 (ήτοι το σύνολο όλων των ζευγών (x,y) με τα x,y να ανήκουν στην εκτεταμένη ευθεία των πραγματικών R = [−∞, +∞] εφοδιασμένο με γινόμενη τοπολογία), το οποίο θα περιέχει όλα τα σημεία στα οποία η συνάρτηση f έχει όριο.
Η f έχει όριο σε όλα τα οριακά σημεία του D εκτός από το (0,0), (+∞,0), (1,+∞) και (1,−∞).[22] Σύμφωνα με αυτό μπορεί κανείς να ορίσει τις δυνάμεις xy διά της συνέχειας οποτεδήποτε 0 ≤ x ≤ +∞, −∞ ≤ y ≤ +∞, ακτό από τα 00, (+∞)0, 1+∞ και 1−∞, τα οποία παραμένουν απροσδιόριστες μορφές.
Υπό αυτόν τον ορισμό διά της συνέχειας, προκύπτει:
- α+∞ = +∞ και α−∞ = 0, όταν 1 < α ≤ +∞.
- α+∞ = 0 και α−∞ = +∞, όταν 0 ≤ α < 1.
- 0b = 0 και (+∞)b = +∞, όταν 0 < b ≤ +∞.
- 0b = +∞ και (+∞)b = 0, όταν −∞ ≤ b < 0.
Αυτές οι δυνάμεις υπολογίζονται παίρνοντας τα όρια του xy για θετικές τιμε΄ς του x. Αυτή η μέθοδος δεν επιτρέπει ορισμό του xy όταν x < 0, καθώς τα ζεύγη (x,y) με x < 0 δεν είναι οριακά σημεία του D.
Από την άλλη, όταν ο n είναι ακέραιος, η δύναμη xn έχει σημασία για όλες τις τιμές του x, συμπεριλαμβανομένων και των αρνητικών. Αυτό μπορεί να κάνει τον ορισμό 0n = +∞ προβληματικό για αρνητικά n όταν το n είναι περιττός, καθώς σε αυτή την περίπτωση tn → +∞ καθώς το t τείνει στο 0 από θετικές τιμές αλλά όχι αρνητικές.
Αποδοτικός υπολογισμός ακέραιας δύναμης[Επεξεργασία | επεξεργασία κώδικα]
Η απλούστερη μέθοδος για τον υπολογισμό αn απαιτεί n−1 πράξεις πολλαπλασιασμού, όμως μπορεί να υπολογιστεί πιο αποδοτικά όπως φαίνεται στο παράδειγμα που ακολουθεί. Για να υπολογιστεί το 2100, ας σημειωθεί ότι 100 = 64 + 32 + 4. Οι υπολογισμοί γίνονται με την ακόλουθη σειρά:
- 22 = 4
- (22)2 = 24 = 16
- (24)2 = 28 = 256
- (28)2 = 216 = 65,536
- (216)2 = 232 = 4,294,967,296
- (232)2 = 264 = 18,446,744,073,709,551,616
- 264 232 24 = 2100 = 1,267,650,600,228,229,401,496,703,205,376
Έτσι απαιτούνται μόνο 8 πράξεις πολλαπλασιασμού αντί για 99 (καθώς το τελευταίο γινόμενο απαιτεί 2 πολλαπλασιαμούς).
Εν γένει, ο αριθμός πράξεων πολλαπλασιασμού που απαιτείται για να υπολογιστεί το αn μπορεί να μειωθεί σε Θ(log n) χρησιμοποιώντας ύψωση σε δύναμη δια του τετραγωνισμού ή (πιο γενικά) ύψωση σε δύναμη με αλυσίδα πρόσθεσης. Βρίσκοντας την ελάχιστη ακολουθία πολλαπλασιασμών (το ελάχιστο μήκος αλυσίδας πρόσθεσης για τον εκθέτη) για το αn είναι δύσκολο πρόβλημα για το οποίο δεν είναι γνωστοί ακόμα αποδοτικοί αλγόριθμοι, υπάρχουν όμως διαθέσιμοι αρκετά αποδοτικοί ευριστικοί αλγόριθμοι.[23]
Εκθετικός συμβολισμός για συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
Τοποθετώντας ένα ακέραιο εκθέτη μετά το όνομα ή το σύμβολο μίας συνάρτησης, σαν η συνάρτηση να υψώνονταν σε δύναμη, κατά κοινή χρήση σημαίνει επεναλαμβανόμενη σύνθεση συναρτήσεων παρά επαναλαμβανόμενο πολλαπλασιασμό. Συνεπώς το f3(x) μπορεί να σημαίνει f(f(f(x))), και πιο συγκεκριμένα το f −1(x) συνήθως συμβολίζει την αντίστροφη συνάρτηση της f. Οι επαναλαμβανόμενες συναρτήσεις έχουν ιδιαίτερο ενδιαφέρον στη μελέτη των φράκταλ και των δυναμικών συστημάτων. Ο Babbage ήταν ο πρώτος που μελέτησε το πρόβλημα εύρεσης της τετραγωνικής ρίζας συνάρτησης f1/2(x).
Για ιστορικούς ωστόσο λόγους, ισχύει ειδική σύνταξη για τις τριγωνομετρικές συναρτήσεις: ένας θετικός εκθέτης στο όνομα της συνάρτησης σημαίνει ότι το αποτέλεσμα υψώνεται σε αυτή τη δύναμη, ενώ ο εκθέτης -1 υποδηλώνει την αντίστροφη συνάρτηση. Έτσι, sin2x είναι απλώς συντομογραφία του (sin x)2 χωρίς την χρήση παρενθέσεων, ενώ το sin−1x αναφέρεται στην αντίστροφη συνάρτηση του ημιτόνου, που ονομάζεται arcsin x.[Σημ. 1] Δεν υπάρχει ανάγκη για συντομογραφίες των αντίστροφων τριγωνομετρικών συναρτήσεων καθώς κάθε μία έχει το δικό της όνομα και συντομογραφία. Για παράδειγμα 1/sin x = (sin x)−1 είναι csc x (συντέμνουσα). Παρόμοια σύμβαση ισχύει και για τους λογάριθμους, όπου log2x συνήθως σημαίνει (log x)2, και όψι log log x.
Γενικεύσεις[Επεξεργασία | επεξεργασία κώδικα]
Στην αφηρημένη άλγεβρα[Επεξεργασία | επεξεργασία κώδικα]
Η ύψωση σε ακέραιο εκθέτη μπορεί να οριστεί για αρκετές γενικές δομές στην αφηρημένη άλγεβρα.
Έσρω X ένα σύνολο με μία προσεταιριστική κατά δύναμη διμελή πράξη η οποία γράφεται πολλαπλασιαστικά. Τότε το xn ορίζεται για κάθε στοιχείο x του X και οποιονδήποτε μη μηδενικό φυσικό αριθμό n ως το γινόμενο n αντιγράφων του x, το οποίο αναδρομικά ορίζεται ως
και έχει τις ακόλουθες ιδιότητες
- (προσεταιριστική κατά δύναμη ιδιότητα),
Αν η πράξη έχει ένα αμφίπλευρο ταυτοτικό στοιχείο 1 (που συχνά συμβολίζεται ως e), τότε το x0 ορίζεται να είναι ίσο με 1 για οποιοδήποτε x.
- αμφίπλευρη ταυτότητα
Αν η πράξη έχει επίσης αμφίπλευρα αντίστροφα στοιχεία, και ο πολλαπλασιασμός είναι προσεταιριστικός τότε το μάγμα είναι ομάδα. Το αντίστροφο του x μπορεί να συμβολιστεί ως x−1 και ακολουθεί όλυος τους σηνήθεις κανόνες των εκθετών.
- Αμφίπλευρη αντιστροφή
- προσεταιριστικότητα
Αν η πράξη του πολλαπλασιασμού είναι αντιμεταθετική (όπως για παράδειγμα στις αβελιανές ομάδες, τότε ισχύει το ακόλουθο:
Αν η διμελής πράξη γραφή προσθετικά, όπως γίνεται συχνά για τις αβελιανές ομάδες, τότε η το δεδομένο «ύψωση σε δύναμη είναι επαναλαμβανόμενος πολλαπλασιασμός» μπορεί να επανερμηνευθεί ως «ο πολλαπλασιασμός είναι επαναλαμβανόμενη πρόσθεση». Έτσι κάθε ένας από τους παραπάνω κανόνες της ύψωσης σε δύναμη έχει το ανάλογό του στους κανόνες του πολλαπλασιασμού.
Όταν υπάρχουν διάφορες πράξεις, οποιαδήποτε από τις οποίες μπορεί να επαναληφθεί εκθετικά, είναι κοινή πρακτική να υπάρχει ένδειξη για το ποια πράξη επαναλαμβάνεται τοποθετώντας το σύμβολό της στον εκθέτη. Έτσι x*n είναι x * ··· * x, ενώ x#n είναι x # ··· # x, οποιεσδήποτε και αν είναι οι πράξεις * και #.
Ο εκθετικός συμβολισμό χρησιμοποιείται επίσης στη θεωρία ομάδων, ώστε να υποδηλώνει συζυγία. Δηλαδή, gh = h−1gh όπου g και h είναι τα στοιχεία κάποιας ομάδας. αν και η συζυγία υπακούει κάποιους κανόνες της ύψωσης σε δύναμη, δεν είναι παράδειγμα επαναλαμβανόμενου πολλαπλασιασμού υπό καμία έννοια.
Στα σύνολα[Επεξεργασία | επεξεργασία κώδικα]
Αν το n είναι φυσικός αριθμός και το A ένα τυχαίο σύνολο, η έκφραση An χρησιμοποιείται συχνά για να δηλώσει το σύνολο διατεταγμένων n-άδων στοιχείων του A. Αυτό είναι αντίστοιχο με το να τεθεί το An να δηλώνει το σύνολο των συναρτήσεων από το σύνολο {0, 1, 2, ..., n−1} στο σύνολο A. Η n-άδα (α0, α1, α2, ..., αn−1) αναπαριστά την συνάρτηση που αντιστοιχεί το i στο ai.
Για ένα άπειρο πληθικό αριθμό κ και ένα σύνολο A, χρησιμοποιείται επίσης ο συμβολισμός Aκ για να υποδηλώσει το σύνολο των συναρτήσεων από ένα σύνολο μεγέθους κ προς το A. Αυτό κάποιες φορές γράφεται κA για να διαχωριστεί από την πληθική ύψωση σε δύναμη, όπως ορίζεται παρακάτω.
Αυτή η γενικευμένη ύψωση σε δύναμη μπορεί να οριστεί και από πράξεις σε σύνολα ή για σύνολα με επιπλέον δομές. Για παράδειγμα, στη γραμμική άλγεβρα, έχει νόημα να τοποθετηθούν δείκτες στο ευθύ άθρισμα διανυσματικών χώρων επί τυχαίων συνόλων δεικτών. Έτσι μπορεί να γίνει:
Όπου κάθε Vi είναι ένας διανυσματικός χώρος/ Τότε αν Vi = V για κάθε i, το ευθύ άθροισμα αυτών μπορεί να γραφτεί με εκθετικό συμβολισμό ως V(+)N, ή πιο απλά VN με την σύμβαση ότι το ευθύ άθροισμα είναι το προκαθορισμένο. Είναι δυνατόν να αντικατασταθεί το σύνολο N με τον πληθικό αριθμό n ώστε να προκύψει Vn, αν και, χωρίς να επιλεγεί ένα συγκεκριμένο σύνολο με πληθικό αριθμό n, αυτό ορίζεται με ακρίβεια ισομορφισμού. Λαμβάνοντας το V ως το πεδίο του R των πραγματικών αριθμών (θεωρούμενο ως διανυσματικός χώρος επί του εαυτού του) και n να είναι κάποιος φυσικός αριθμός, προκύπτει ο Ευκλείδιος χώρος Rn.
Αν στη βάση μιας πράξης ύψωσης σε δύναμη βρίσκεται ένα σύνολο, η πράξη της ύψωσης είναι το καρτεσιανό γινόμενο εκτός αν δηλωθεί διαφορετικά. Καθώς πολλαπλά καρτεσιανά γινόμενα παράγουν μία n-πλειάδα, η οποία αναπαρίσταται από μία συνάρτηση σε ένα σύνολο με κατάλληλο πληθικό αριθμό, το SN γίνεται απλά το σύνολο όλων των συναρτήσεων από το N στο S:
Αυτό ταιριάζει με την ύψωση σε δύναμη πληθικών αριθμών, με την έννοια ότι |SN| = |S||N|, όπου |X| είναι ο πληθικός αριθμός του X. Όταν N=2={0,1}, έχουμε |2X| = 2|X|, όπου το 2X, το οποίο συνήθως συμβολίζεται PX, είναι το δυναμοσύνολο του X, κάθε υποσύνολο Y του X αντιστοιχεί μοναδικά σε μία συνάρτηση στο X που παίρνει την τιμή 1 για x ∈ Y και 0 για x ∉ Y.
Στη θεωρία κατηγοριών[Επεξεργασία | επεξεργασία κώδικα]
Σε μία κλειστή καρτεσιανή κατηγορία η εκθετική πράξη μπορεί να χρησιμοποιηθεί για την ύψωση ενός τυχαίου αντικειμένου στη δύναμη ενός άλλου τυχαίου αντικειμένου. Αυτό γενικεύει το καρτεσιανό γινόμενο στην κατηγορία των συνόλων. Αν είναι ένα αρχικό αντικείμενο σε μία καρτεσιανή κλειστή κατηγορία, τότε το εκθετικό αντικείμενο είναι ισομορφικό με οποιοδήποτε τερματικό αντικείμενο .
Επαναλαμβανόμενη ύψωση σε δύναμη[Επεξεργασία | επεξεργασία κώδικα]
Όπως η ύψωση σε δύναμη φυσικών αριθμών είναι στην ουσία επαναλαμβανόμενος πολλαπλασιασμός, είναι πιθανό να οριστεί μία πράξη με βάση την επαναλαμβανόμενη ύψωση σε δύναμη. Αυτή η πράξη κάποιες φορές ονομάζεται tetration. Η επανάληψη του tetration οδηγεί σε άλλη πράξη και ούτω καθεξής. Αυτή η ακολουθία πράξεων εκφράζεται από την συνάρτηση Ackermann και τον συμβολισμό άνω βέλους Knuth. Όπως ακριβώς η δύναμη αυξάνεται ταχύτερα από ότι ο πολλαπλασιασμό, και με την σειρά του ο πολλαπλασιασμός ταχύτερα από την πρόσθεση, η δύναμη της δύναμης αυξάνει ταχύτερα από την δύναμη. Αποτιμημένες στο (3,3), η πράξεις της πρόσθεσης, πολλαπλασιασμού, ύψωσης σε δύναμη και tetration δίνουν 6, 9, 27, και 7,625,597,484,987 αντίστοιχα.
Στις γλώσσες προγραμματισμού[Επεξεργασία | επεξεργασία κώδικα]
Ο συμβολισμός με εκθέτη xy είναι βολικός στο χειρόγραφο αλλά μη πρακτικός για τις γραφομηχνές και τα τερματικά που έχουν όλους τους χαρακτήρες ευθυγραμισμένους. Πολλές γλώσσες προγραμματισμού έχουν εναλακτικούς τρόπους για την έκφαρση της ύψωσης σε δύναμη που δεν χρησιμοποιούν εκθέτες:
- x ↑ y: Algol, Commodore BASIC
- x ^ y: BASIC, J, MATLAB, R, Microsoft Excel, TeX (και τα παράγωγά του), TI-BASIC, bc (για ακέραιους εκθέτες), Haskell (για μη αρνητικούς ακέραιους εκθέτες), Lua, ASP και τα περισσότερα υπολογιστικά συστήματα άλγεβρας (CAS)
- x ^^ y: Haskell (για κλασματική βάση, ακέραιους εκθέτες), D
- x ** y: Ada, Bash, COBOL, Fortran, FoxPro, Gnuplot, OCaml, Perl, PL/I, Python, Rexx, Ruby, SAS, Tcl, ABAP, Haskell (για εκθέτες μεταβλητής υποδιαστολής), Turing, VHDL
- x⋆y: APL
- Power(x, y): Microsoft Excel, Delphi/Pascal
- pow(x, y): C, C++, PHP, Tcl
- x**y: Python
- Math.pow(x, y): Java, JavaScript, Modula-3, Standard ML
- Math.Pow(x, y) ή BigInteger.Pow(x, y): C# (και άλλες γλώσσες που χρησιμοποιούν την BCL)
- (expt x y): Common Lisp, Scheme
- math:pow(x, y): Erlang
Στις Bash, C, C++, C#, Java, JavaScript, Perl, PHP, Python και Ruby, το σύμβολο ^ αναπαριστά το επιπέδου bit XOR. Στην Pascal αναπαριστά την έμμεση αναφορά. Στις OCaml και Standard ML αναπαριστά παράθεση συμβολοσειρών (string concatenation).
Ιστορία του συμβολισμού[Επεξεργασία | επεξεργασία κώδικα]
Ο όρος δύναμη χρησιμοποιήθηε από τον έλληνα μαθηματικό Ευκλείδη για το τετράγωνο μίας ευθείας.[24] Τον 9ο αιώνα, ο Αλ Χουαρίζμι χρησιμοποίησε τους όρους mal για το τετράγωνο και kab για τον κύβο, τα οποία μεταγενέστεροι ισλαμιστές μαθηματικοί τα αναπαριστούσαν ως m και k αντίστοιχα, κατά τον 15ο αιώνα, όπως φαίνεται στο έργο του Αμπού αλ-Χασάν ιμπν Αλί αλ-Καλασαντί.[25]
Ο Nicolas Chuquet χρησιμοποίησε μία μορφή εκθετικού συμβολισμού τον 15ο αιώνα, η οποία χρησιμοποιήθηκε αργότερα από τον Henricus Grammateus και τον Μίχαελ Στίφελ τον 16ο αιώνα. Ο Σάμιουελ Τζικ (Samuel Jeake) εισήγαγε τον όρο indices (δείκτες) το 1696.[24] Τον 16ο αιώνα ο Robert Recorde χρησιμοποίησε τους όρους τετράγωνο, κύβος, zenzizenzic (για την τέταρτη δύναμη), surfolide (πέμπτη), zenzicube (έκτη), second surfolide (εβδόμη) και Zenzizenzizenzic (ογδόη).
Κάποιοι μαθηματικοί (όπως π.χ. ο Ισαάκ Νεύτων) χρησιμοποίησαν εκθέτες μόνο για δυνάμεις μεγαλύτερες του δύο, προτιμώντας να αναπαριστούν τα τετράγωνα ως επαναλαμβανόμενο πολλαπλασιασμό. Έτσι έγραφαν τα πολυώνυμα ως ax + bxx + cx3 + d.
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Το ίδιο ισχύει και για τον συμβολισμό που εμφανίζεται ενίοτε στην ελληνική βιβλιογραφία. Έτσι για παράδειγμα ημ 2x ισοδυναμεί με (ημ x)2, και ημ−1x συμβολίζει την αντίστροφη συνάρτηση, τόξο ημιτόνου, τοξημ x
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Αυτός ο ορισμός της κύριας ρίζας της μονάδας μπορεί να βρεθεί στα:
- Cormen, Thomas H.· Leiserson, Charles E.· Rivest, Ronald L.· Stein, Clifford (2009). Introduction to algorithms (3η έκδοση). Cambridge, Mass.: MIT Press. σελίδες 171. ISBN 0-262-03384-4.
- Cull, Paul· Flahive, Mary· Robson, Robby (2005). Difference Equations: From Rabbits to Chaos (Undergraduate Texts in Mathematics έκδοση). Springer. ISBN 0387232346. Ορισμός στη σελ. 351
- "Principal root of unity", MathWorld.
- ↑ Complex number to a complex power may be real at Cut The Knot gives some references to ii
- ↑ Steiner J, Clausen T, Abel NH (1827). «Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen». Journal für die reine und angewandte Mathematik 2: 286–287. http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=270662.[νεκρός σύνδεσμος]
- ↑ N. Bourbaki, Elements of Mathematics, Theory of Sets, Springer-Verlag, 2004, III.§3.5.
- ↑ «Κάποια συγγράμματα αφήνουν την ποσότητα 00 αόριστη, επειδή οι συναρτήσεις x0 και 0x έχουν διαφορετικά όρια όταν το x τείνει στο 0. Όμως αυτό είναι λάθος. Πρέπει να ορίσουμε το x0 = 1, για όλα τα x, αν είναι το διωνυμικό θεώρημα να είναι έγκυρο όταν x = 0, y = 0, και/ή x = −y. Το διωνυμικό θεώρημα είναι πολύ σημαντικό ώστε να μένει περιορισμένο αυθαίρετα! Αντιθέτως η συνάρτηση 0x είναι σχεδόν ασήμαντη».Ronald Graham· Donald Knuth· Oren Patashnik (5 Ιανουαρίου 1989). «Binomial coefficients». Concrete Mathematics (1st έκδοση). Addison Wesley Longman Publishing Co. σελ. 162. ISBN 0-201-14236-8.
- ↑ Malik, S. C.· Arora, Savita (1992). Mathematical Analysis. New York: Wiley. σελ. 223. ISBN 978-8122403237.
Εν γένει το όριο της φ(x)/ψ(x) όταν x=α στην περίπτωση που τα όρια και των δύο συναρτήσεων υπάρχουν είναι ίση με το όριο του αριθμητή διαιρεμένο με τον παρονομαστή. Αλλά τι γίνεται όταν και τα δύο όρια είναι μηδέν; Η διαίρεση (0/0) δεν έχει νόημα. Μία περίπτωση όπως αυτή είναι γνωστή ως απροσδιόριστη μορφή. Άλλες τέτοιες μορφές είναι ∞/∞ 0×∞, ∞−∞, 00, 1∞ και ∞0.
- ↑ L. J. Paige (March 1954). «A note on indeterminate forms». American Mathematical Monthly 61 (3): 189–190. doi:. http://jstor.org/stable/2307224.
- ↑ sci.math FAQ: What is 0^0?
- ↑ Rotando, Louis M.; Korn, Henry (1977). «The Indeterminate Form 00». Mathematics Magazine (Mathematical Association of America) 50 (1): 41–42. doi:. http://jstor.org/stable/2689754.
- ↑ Lipkin, Leonard J. (2003). «On the Indeterminate Form 00». The College Mathematics Journal (Mathematical Association of America) 34 (1): 55–56. doi:. http://jstor.org/stable/3595845.
- ↑ "... Ας αρχίσουμε από το x = 0. Εδώ το xx είναι αόριστο." Mark D. Meyerson, The xx Spindle, Mathematics Magazine 69, no. 3 (June 1996), 198-206.
- ↑ Παραδείγματα περιλαμβάνουν τους: Edwards and Penny (1994). Calculus, 4th ed, Prentice-Hall, p. 466, and Keedy, Bittinger, and Smith (1982). Algebra Two. Addison-Wesley, p. 32.
- ↑ Donald C. Benson, The Moment of Proof : Mathematical Epiphanies. New York Oxford University Press (UK), 1999. ISBN 978-0-19-511721-9
- ↑ 14,0 14,1 Donald E. Knuth, Two notes on notation, Amer. Math. Monthly 99 no. 5 (May 1992), 403–422.
- ↑ Augustin-Louis Cauchy, Cours d'Analyse de l'École Royale Polytechnique (1821). In his Oeuvres Complètes, series 2, volume 3.
- ↑ Guillaume Libri, Note sur les valeurs de la fonction , Journal für die reine und angewandte Mathematik 6 (1830), 67–72.
- ↑ Guillaume Libri, Mémoire sur les fonctions discontinues, Journal für die reine und angewandte Mathematik 10 (1833), 303–316.
- ↑ A. F. Möbius, Beweis der Gleichung 00 = 1, nach J. F. Pfaff, Journal für die reine und angewandte Mathematik 12 (1834), 134–136.
- ↑ Handbook of Floating-Point Arithmetic. Birkhäuser Boston. 2009. σελ. 216. ISBN 978-0817647049.
- ↑ John Benito (April 2003) (PDF). Rationale for International Standard—Programming Languages—C. Revision 5.10, σελ. 182. http://www.open-std.org/jtc1/sc22/wg14/www/C99RationaleV5.10.pdf.
- ↑ «.NET Framework Class Library Math.Pow Method». Microsoft.
- ↑ N. Bourbaki, Topologie générale, V.4.2.
- ↑ Gordon, D. M. 1998. A survey of fast exponentiation methods. J. Algorithms 27, 1 (Apr. 1998), 129-146. doi:http://dx.doi.org/10.1006/jagm.1997.0913
- ↑ 24,0 24,1 O'Connor, John J.; Robertson, Edmund F., «Etymology of some common mathematical terms», MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Miscellaneous/Mathematical_notation.html, ανακτήθηκε στις 2011-07-04
- ↑ O'Connor, John J.; Robertson, Edmund F., «Abu'l Hasan ibn Ali al Qalasadi», MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Qalasadi.html
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
|















![{\displaystyle a^{m/n}=\left(a^{m}\right)^{1/n}={\sqrt[{n}]{a^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1663246fb7456433a31022e2211e563eefd43b5)







![{\displaystyle 5^{x}\approx 5^{1.732}=5^{433/250}={\sqrt[{250}]{5^{433}}}\approx 16.241.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0e4ff69a91b030c3ae17497000e448f9e75fe13)












![{\displaystyle \left(r^{c}e^{-d\theta }\right)e^{i(d\log r+c\theta )}=\left(r^{c}e^{-d\theta }\right)\left[\cos(d\log r+c\theta )+i\sin(d\log r+c\theta )\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e82ef3ebfb202936422ac0011f1d31ec904279c5)














































