Διακριτός μετασχηματισμός Φουριέ
| Αυτό το λήμμα χρειάζεται επιμέλεια ώστε να ανταποκρίνεται σε υψηλότερες προδιαγραφές ορθογραφικής και συντακτικής ποιότητας ή μορφοποίησης. Αίτιο: ορολογία, μετάφραση, μορφοποίηση Για περαιτέρω βοήθεια, δείτε τα λήμματα πώς να επεξεργαστείτε μια σελίδα και τον οδηγό μορφοποίησης λημμάτων. |

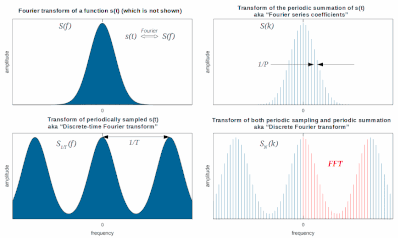
Στα μαθηματικά, ο διακριτός μετασχηματισμός Fourier (DFT) μετατρέπει μια πεπερασμένη ακολουθία από ίσα διαστήματα δειγμάτων από μια συνάρτηση σε μία λίστα με συντελεστές από ένα πεπερασμένο συνδυασμό ημιτονοειδών μιγαδικών αριθμών, καθορισμένων από τις συχνότητες τους, που έχει τις ίδιες τιμές δείγματος. Αυτό μπορεί να ειπωθεί για τη μετατροπή του δείγματος της συνάρτησης από το αρχικό του πεδίο ορισμού (συχνά το χρόνο ή τη θέση κατά μήκος της γραμμής) στο πεδίο της συχνότητας.
Τα δείγματα εισαγωγής είναι μιγαδικοί αριθμοί (στην πράξη, συνήθως πραγματικοί αριθμοί), και οι συντελεστές στο αποτέλεσμα είναι και αυτοί μιγαδικοί . Οι συχνότητες των ημιτονοειδών που προκύπτουν είναι ακέραια πολλαπλάσια της θεμελιώδους συχνότητας, του οποίου η αντίστοιχη περίοδο είναι το μήκος του διαστήματος δειγματοληψίας. Ο συνδυασμός των ημιτονοειδών που λαμβάνονται μέσω του DFT είναι επομένως περιοδική με την ίδια περίοδο. Ο DFT(διακριτός μετασχηματισμός Fourie) διαφέρει από τον διακριτού χρόνου μετασχηματισμό Fourier (DTFT) στην είσοδο τους και στο αποτέλεσμα οι ακολουθίες είναι και οι δύο πεπερασμένες, είναι ως εκ τούτου η λεγόμενη ανάλυση Fourier των πεπερασμένων (ή περιοδικών) διακριτού χρόνου συναρτήσεων.
Ο DFT είναι ο πιο σημαντικός διακριτός μετασχηματισμός, που χρησιμοποιείται για να εκτελέσει την ανάλυση Fourier σε πολλές πρακτικές εφαρμογές.[1] Στην ψηφιακή επεξεργασία σήματος, η συνάρτηση είναι οποιαδήποτε ποσότητα ή σήμα που ποικίλει με την πάροδο του χρόνου, όπως η πίεση των ηχητικών κυμάτων, ένα σήμα ραδιοφώνου ή ημερήσιες μετρήσεις της θερμοκρασίας, δειγματοληψίες πάνω από ένα πεπερασμένο χρονικό διάστημα (συνήθως ορίζεται από μία συνάρτηση παραθύρου[2]). Στην επεξεργασία εικόνας, τα δείγματα μπορεί να είναι οι τιμές των pixels κατά μήκος της γραμμής ή της στήλης των εικόνων raster. Ο DFT , επίσης, χρησιμοποιείται για την αποτελεσματική επίλυση μερικών διαφορικών εξισώσεων, και για να εκτελέσει άλλες ενέργειες, όπως ο συσχετισμός συναρτήσεων ή ο πολλαπλασιασμός μεγάλων ακεραίων.
Δεδομένου ότι πρόκειται για ένα πεπερασμένο ποσό των δεδομένων, μπορεί να εφαρμοστεί σε υπολογιστές με αριθμητικούς αλγόριθμους ή ακόμα και με ειδικά υλικά. Αυτές οι εφαρμογές συνήθως χρησιμοποιούν αποτελεσματικά τον γρήγορο μετασχηματισμό Fourier (FFT) σε αλγορίθμους;[3] τόσο πολύ, που οι όροι "FFT" και "DFT" συχνά χρησιμοποιούνται εναλλακτικά. Πριν από την τρέχουσα χρήση, το "FFT" μπορεί επίσης να έχει χρησιμοποιηθεί για τον ασαφή όρο "πεπερασμένος μετασχηματισμός Fourier".
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Η ακολουθία των N μιγαδικών αριθμών μετατρέπεται σε μία N-περιοδική ακολουθία μιγαδικών αριθμών:
Λόγω της περιοδικότητας, το σύνηθες πεδίο ορισμού της k υπολογίζεται ότι είναι το [0, N − 1]. Αυτή είναι η περίπτωση ισχύει πάντα, όταν ο DFT υλοποιείται μέσω του αλγόριθμου για τον γρήγορα μετασχηματισμό Fourier(FFT). Αλλά και άλλες κοινές περιοχές είναι το [−N/2, N/2 − 1] (N άρτιος ) και [−(N − 1)/2, (N − 1)/2] (N περιττός), όπως όταν το αριστερό και το δεξί ήμισυ ενός FFT ως αποτέλεσμα μιας ακολουθίας έχουν ανταλλαχθεί.[4]
Ο μετασχηματισμός μερικές φορές συμβολίζεται με το σύμβολο , όπως και ή ή .[note 1]
Eq.1 μπορεί να ερμηνευθεί ή να περιγραφεί με διάφορους τρόπους, για παράδειγμα:
- Περιγράφει πλήρως τον διακριτού χρόνου μετασχηματισμό Fourier (DTFT) μιας N-περιοδικής ακολουθίας, η οποία περιλαμβάνει μόνο στοιχεία με διακριτή συχνότητα . (Χρησιμοποιώντας τον DTFT με περιοδικά δεδομένα)
- Μπορεί επίσης να παρέχει ομοιόμορφα κατανεμημένα δείγματα της συνεχούς DTFT μιας πεπερασμένου μήκους ακολουθία. (Δειγματοληψία του DTFT)
- Είναι η οριζόντια συσχέτιση της εισαγόμενης ακολουθίας xn, και μία μιγαδικά ημιτονοειδής στη συχνότητα k/N. Έτσι λειτουργεί σαν ένα προσαρμοσμένο φίλτρο για αυτή τη συχνότητα.
- Είναι μία διακριτή αναλογία του τύπου για τους συντελεστές της σειράς Fourier:
- η οποίο είναι, επίσης, N-περιοδική. Για πεδίο ορισμού αυτό είναι ο αντίστροφος μετασχηματισμός του Eq.1. Σε αυτή την ερμηνεία, το κάθε είναι ένας μιγαδικός αριθμός που κωδικοποιεί και το εύρος και τη φάση του μια ημιτονοειδή συνιστώσα της συνάρτησης Η ημιτονοειδής συχνότητα είναι k κύκλους ανά N δείγματα. Το εύρος της και η φάση της είναι:
- πού atan2 είναι μία μορφή της arctan συνάρτησης.
Ο ομαλός πολλαπλασιασμός των συντελεστών του DFT και IDFT (εδώ το 1 και 1/N) και τα σύμβολα των εκθετών είναι απλώς συμβάσεις, και διαφέρουν σε ορισμένες χρήσεις. Οι μόνες απαιτήσεις αυτών των συμβάσεων είναι ότι ο DFT και IDFT έχουν αντίθετο-σύμβολα στους εκθέτες και το αποτέλεσμα από την ομαλοποίηση των συντελεστών τους είναι 1/N. Μια ομαλοποίηση της τόσο για τον DFT όσο και για τον IDFT, για παράδειγμα, κάνει τον μετασχηματισμό μοναδικό.
Στη συζήτηση που ακολουθεί οι όροι "ακολουθία" και "διάνυσμα" θα θεωρούνται εναλλάξιμoi.
Χρησιμοποιώντας τον τύπο του Euler, ο DFT τύπος μπορεί να μετατραπεί σε τριγωνομετρικές μορφές που μερικές φορές χρησιμοποιείται στη μηχανική και την επιστήμη των υπολογιστών:
Μετασχηματισμός Fourier:
Αντίστροφος μετασχηματισμός Fourier:
- N = αριθμός των δείγματων που έχουμε
- n = το τρέχον δείγμα που εξετάζουμε (0, ..., N − 1)
- xn = αξία του συμβόλου στο χρόνο n
- k = τρέχουσα συχνότητα που εξετάζουμε (0 Hertz έως N-1 Hertz)
- Xk = ποσό της συχνότητας k στο σύμβολο (το εύρος και τη φάση, ένας μιγαδικός αριθμός)
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Πληρότητα[Επεξεργασία | επεξεργασία κώδικα]
Ο διακριτός μετασχηματισμός Fourier είναι ένας αντιστρέψιμος, γραμμικός μετασχηματισμός
με το που σημαίνει το σύνολο των μιγαδικών αριθμών. Με άλλα λόγια, για κάθε N > 0, ένα N-διαστάσεων μιγαδικό διάνυσμα έχει ένα DFT και IDFT τα οποία είναι με τη σειρά τους N-διαστάσεων μιγαδικά δiανύσματα.
Καθετότητα[Επεξεργασία | επεξεργασία κώδικα]
Τα διανύσματα σχηματίζουν μια ορθογώνια βάση πάνω από το σύνολο των N-διαστάσεων μιγαδικών διανυσμάτων:
πού είναι το δέλτα του Kronecker. (Στο τελευταίο βήμα, το άθροισμα είναι ασήμαντο αν , όπου είναι 1+1+⋅⋅⋅=N, και το αντίθετο, είναι μια γεωμετρική σειρά που μπορεί να αθροιστεί αναλυτικώς για να αποκτήσει το μηδέν.) Αυτή η συνθήκη της καθετότητας μπορεί να χρησιμοποιηθεί για να αποκομίσει τον τύπο για την IDFT από τον ορισμό του DFT, και είναι ισοδύναμο με τη μοναδική ιδιότητα παρακάτω.
Το Plancherel θεώρημα και το θεώρημα του Parseval[Επεξεργασία | επεξεργασία κώδικα]
Αν Xk και Yk είναι το DFTs των xn και yn , αντίστοιχα, τότε το θεώρημα του Parseval παραθέτει:
όπου ο αστερίσκος δηλώνει συζυγή μιγαδικό αριθμό.Το Plancherel θεώρημα είναι μια ειδική περίπτωση από το θεώρημα του Parseval και παραθέτει:
Αυτά τα θεωρήματα είναι επίσης ισοδύναμο με τη μοναδική συνθήκη παρακάτω.
Περιοδικότητα[Επεξεργασία | επεξεργασία κώδικα]
Η περιοδικότητα μπορεί να αποδειχθεί άμεσα από τον ορισμό:
Ομοίως, μπορεί να αποδειχθεί ότι ο τύπος IDFT οδηγεί σε μια περιοδική επέκταση.
Θεώρημα μετατόπισης[Επεξεργασία | επεξεργασία κώδικα]
Πολλαπλασιάζοντας με μία γραμμική φάση για κάποιο ακέραιο m αντιστοιχεί σε μια κυκλική μετατόπιση των αποτελεσμάτων : αντικαθίσταται από , όπου ο δείκτης ερμηνεύεται ως αριθμητικό υπόλοιπο(του Νδηλαδή, σε τακτά χρονικά διαστήματα). Ομοίως, μια κυκλική μετατόπιση της εισόδου αντιστοιχεί σε πολλαπλασιασμό του αποτελέσματος από μια γραμμική φάση. Μαθηματικά, αν αντιπροσωπεύει το διάνυσμα x τότε
- αν
- στη συνέχεια
- και
Θεώρημα κυκλικής συνέλιξης και το θεώρημα συσχέτισης[Επεξεργασία | επεξεργασία κώδικα]
Το θεώρημα συνέλιξης για το χρονικό-διακριτό μετασχηματισμό Fourier δείχνει ότι συνέλιξη των δύο άπειρων ακολουθιών μπορούν να ληφθούν ως ο αντίστροφος μετασχηματισμός των προϊόντων των ατομικών μετασχηματισμών. Μια σημαντική απλοποίηση προκύπτει όταν οι ακολουθίες έχουν πεπερασμένο μήκος, N. Όσον αφορά το DFT και το αντίστροφο DFT, μπορεί να γραφτεί ως εξής:
που είναι η συνέλιξη της ακολουθίας με μια ακολουθία εκτεταμένη με σειρά περιοδικής άθροισης:
Ομοίως, η συσχέτισή της και δίνεται από:
Όταν κάθε ακολουθία περιέχει μια σειρά από μηδενικά, μήκους L, L+1 από τα αποτελέσματα των κυκλικών συνελέξεων είναι ισοδύναμα με τις αξίες των Μέθοδοι έχουν αναπτυχθεί επίσης για να χρησιμοποιηθεί αυτή η ιδιότητα ως μέρος μιας αποτελεσματικής διαδικασίας που κατασκευάζει με μία ή ακολουθία ενδεχομένως πολύ μεγαλύτερη από το μέγεθος του πρακτικού μετασχηματισμού (N). Δύο τέτοιες μέθοδοι ονομάζονται επικάλυψη-αποθήκευση και επικάλυψη-προσθήκη.[5] Η αποδοτικότητα προκύπτει από το γεγονός ότι μια άμεση αξιολόγηση της κάθε άθροισης (παραπάνω) απαιτεί διαδικασίες για την παράγωγη ακολουθία μήκους N. Μια έμμεση μέθοδος, χρησιμοποιώντας μετασχηματισμούς, μπορεί να επωφεληθεί από την αποδοτικότητα του γρήγορου μετασχημαισμού Φουριε (ΓΜΦ) για να επιτύχει πολύ καλύτερες επιδόσεις. Επιπλέον, οι περιελίξεις μπορούν να χρησιμοποιηθούν για να υπολογίσουν αποτελεσματικά DFTs μέσω του αλγορίθμου Rader FFT και του Bluestein αλγόριθμο FFT.
Δυαδικότητα θεωρήματος συνέλιξης[Επεξεργασία | επεξεργασία κώδικα]
Μπορεί, επίσης, να αποδειχθεί ότι:
-
- που είναι η κυκλική συνέλιξη των και .
Τριγωνομετρικό πολυώνυμο παρεμβολής[Επεξεργασία | επεξεργασία κώδικα]
Το τριγωνομετρικό πολυώνυμο παρεμβολής
- για N άρτιος ,
- για N περιττός,
όπου οι συντελεστές του Xk δίνεται από τον DFT της xn παραπάνω, ικανοποιούν την ιδιότητα παρεμβολής για .
Για άρτιο N, παρατηρούμε ότι η συχνότητα Nyquist component αντιμετωπίζεται ειδικά.
Αυτή η παρεμβολή δεν είναι μοναδική: aliasing σημαίνει ότι θα μπορούσε κανείς να προσθέσει N σε κάθε μιγαδική-ημιτονοειδή συχνότητες (π. χ. αλλαγή να ) χωρίς να αλλάζει η ιδιότητα παρεμβολής, αλλά δίνοντας διαφορετικές τιμές μεταξύ των σημείων. Η επιλογή παραπάνω, ωστόσο, είναι χαρακτηριστική, διότι έχει δύο χρήσιμες ιδιότητες. Η πρώτη, αποτελείται από ημιτονοειδή κύματα των οποίων οι συχνότητες έχουν το μικρότερο δυνατό μεγέθος: η παρεμβολή είναι περιορισμένου εύρους. Ενώ η δεύτερη, αν είναι πραγματικοί αριθμοί, τότε είναι πραγματικό.
Σε αντίθεση, το πιο προφανές τριγωνομετρικό πολυώνυμο παρεμβολής είναι εκείνο στο οποίο οι συχνότητες κυμαίνονται από 0 έως (σε αντίθεση με να όπως παραπάνω), παρόμοιο με τον αντίστροφο τύπο DFT. Αυτή η παρεμβολή δεν ελαχιστοποιεί την κλίση, και δεν είναι γενικά πραγματικής-τιμής για πραγματικό *, η χρήση του είναι ένα κοινό λάθος.
Το ενιαίο DFT[Επεξεργασία | επεξεργασία κώδικα]
Ένας άλλος τρόπος θεώρησης του DFT είναι να σημειωθεί ότι στην παραπάνω συζήτηση, ο DFT μπορεί να εκφραστέι ως ο πινακας ΔΜΦ, πίνακας Βαντερμόντ, που εισήγαγε ο Σιλβέστερ το 1867,
όπου
είναι μια πρωτόγονη Νιοστή ρίζα της ενότητας.
Ο αντίστροφος μετασχηματισμός, στη συνέχεια, δίνεται από τον αντίστροφο του παραπάνω πίνακα,
Με ενιαίες ομαλοποιημένες σταθερές , ο DFT γίνεται ένας ενιαίος μετασχηματισμός, που ορίζεται από έναν ενιαίο πίνακα:
όπου det() είναι η ορίζουσα συνάρτηση. Η ορίζουσα είναι το γινόμενο των ιδιοτιμών, η οποία είναι πάντα ή όπως περιγράφεται παρακάτω. Σε ένα πραγματικό διανυσματικό χώρο, ένας ενιαίος μετασχηματισμός μπορεί να θεωρηθεί απλά ως μία άκαμπτη περιστροφή του συστήματος συντεταγμένων, καθώς και όλες οι ιδιότητες μίας άκαμπτης περιστροφής μπορεί να βρεθεί στον ενιαίο DFT.
Η καθετότητα του DFT εκφράζεται τώρα ως ορθοκανονική κατάσταση (η οποία προκύπτει σε πολλούς τομείς των μαθηματικών, όπως περιγράφεται στην ρίζα της ενότητας):
Αν X ορίζεται ως ο ενιαίος DFT του διανύσματος x, τότε
και το Plancherel θεώρημα εκφράζεται ως
Αν δείτε το DFT ως ένα μετασχηματισμό συντεταγμένων, ο οποίος απλώς καθορίζει τις συνιστώσες ενός διανύσματος σε ένα νέο σύστημα συντεταγμένων, τότε η παραπάνω είναι η δήλωση ότι το dot γινόμενο των δύο διανυσμάτων διατηρείται κάτω από έναν ενιαίο μετασχηματισμό DFT. Για την ειδική περίπτωση , αυτό σημαίνει ότι το μήκος ενός διανύσματος είναι διατηρημένο, καθώς και—αυτό είναι το θεώρημα του Parseval,
Συνέπεια του θεωρήματος κυκλικής συνέλιξης είναι ότι ο DFT matrix F διαγωνιοποιεί κάθε circulant πίνακα.
Εκφράζοντας τον αντίστροφο DFT σε όρους του DFT[Επεξεργασία | επεξεργασία κώδικα]
Μια χρήσιμη ιδιότητα του DFT είναι ότι ο αντίστροφος DFT μπορεί εύκολα να εκφραστεί σε όρους του (forward) DFT, μέσω διαφόρων γνωστών "κόλπων". (Για παράδειγμα, σε υπολογισμούς, είναι συχνά βολικό να εφαρμόστει ένας γρήγορος μετασχηματισμός Φουριέ που αντιστοιχεί σε μία κατεύθυνση μετασχηματισμού και, στη συνέχεια, να πάρει την άλλη κατεύθυνση μετασχηματισμού από την πρώτη.)
Πρώτα, μπορούμε να υπολογίσουμε τον αντίστροφο DFT αντιστρέφοντας τις εισόδους (Duhamel et al., 1988):
(Ως συνήθως, οι δείκτες ερμηνεύονται modulo N * έτσι, για να έχουμε .)
Δεύτερον, κάποιος μπορεί επίσης να συζεύξει τις εισόδους και εξόδους:
Τρίτον, μια παραλλαγή αυτού του κόλπου σύζευξης, η οποία είναι μερικές φορές προτιμότερη, επειδή δεν απαιτεί καμία τροποποίηση των δεδομένων των τιμών, συνεπάγεται την εναλλαγή πραγματικών και φανταστικών μερών (η οποία μπορεί να γίνει σε έναν υπολογιστή απλά τροποποιώντας δείκτες). Ορίστε swap() με τα πραγματικά και φανταστικά μέρη ανταλλαγμένα—ότι είναι, αν στη συνέχεια swap() . Αντίστοιχα, swap() ισούται με . Στη συνέχεια
Δηλαδή, ο αντίστροφος μετασχηματισμός είναι ο ίδιος με τον forward μετασχηματισμό με τα πραγματικά και φανταστικά μέρη ανταλλαγμένα τόσο για την εισαγωγή και την παραγωγή, μέχρι την ομαλοποίηση (Duhamel et al., 1988).
Το κόλπο σύζευξης μπορεί επίσης να χρησιμοποιηθεί για να ορίσετε ένα νέο μετασχηματισμό, που σχετίζεται στενά με τον DFT, που είναι συνελιγμένη, που είναι ο δικός του αντίστροφος. Ειδικότερα, είναι καθαρά ο δικός του αντίστροφος: . Ένας στενά συνδεδεμένος συνελιγμένος μετασχηματισμός (με το συντελεστή (1+i) /√2) , δεδομένου ότι οι παράγοντες να ακυρώσει το 2. Για πραγματικές εισροές , το πραγματικό μέρος του δεν είναι άλλο από το διακριτό μετασχηματισμό Hartley, ο οποίος είναι επίσης συνελιγμένος.
Ιδιοτιμές και ιδιοδιανύσματα[Επεξεργασία | επεξεργασία κώδικα]
Οι ιδιοτιμές του DFT πίνακα είναι απλές και γνωστές, ότι τα ιδιοδιανύσματα είναι περίπλοκα, δεν είναι μοναδικά, και αποτελούν αντικείμενο της εν εξελίξει έρευνας.
Σκεφτείτε την ενιαία μορφή που ορίζεται παραπάνω για τον DFT μήκους N, όπου
Ο πίνακας αυτός ικανοποιεί την εξίσωση πολυωνυμικού πίνακα:
Αυτό μπορούμε να το δούμε από τις αντίστροφες ιδιότητες παραπάνω: λειτουργούν δύο φορές δίνοντας τα αρχικά δεδομένα σε αντίστροφη σειρά, έτσι ώστε λειτουργώντας τέσσερις φορές δίνει πίσω τα αρχικά δεδομένα και επισης τον ταυτοτικός πίνακας. Αυτό σημαίνει ότι οι ιδιοτιμές ικανοποιούν την εξίσωση:
Συνεπώς, οι ιδιοτιμές του είναι οι τέσσερις ρίζες της ενότητας: +1, -1, +i, −i.
Δεδομένου ότι υπάρχουν μόνο τέσσερις διακριτές ιδιοτιμές για αυτό το πίνακα, έχουν κάποια πολλαπλότητα. Η πολλαπλότητα δίνει τον αριθμό των γραμμικά ανεξάρτητων ιδιοδιανυσμάτων που αντιστοιχούν σε κάθε ιδιοτιμές. (Σημειώστε ότι υπάρχουν N ανεξάρτητα ιδιοδιανύσματα,ένας ενιαίος πίνακας δεν είναι ελαττωματικό.)
Το πρόβλημα της πολλαπλότητας λύθηκε απο τους McClellan και Parks (1972), αν και αργότερα φαίνεται να είναι ισοδύναμο με το πρόβλημα που λύθηκε από τον Gauss (Dickinson και Steiglitz, 1982). Η πολλαπλότητα εξαρτάται από την τιμή του N modulo 4, και δίνεται από τον ακόλουθο πίνακα:
| μέγεθος N | λ = +1 | λ = -1 | λ = - - | λ = + - |
|---|---|---|---|---|
| 4m | m + 1 | m | m | m − 1 |
| 4m + 1 | m + 1 | m | m | m |
| 4m + 2 | m + 1 | m + 1 | m | m |
| 4m + 3 | m + 1 | m + 1 | m + 1 | m |
Αναφέρεται διαφορετικά, το χαρακτηριστικό πολυώνυμο του είναι:
Κανένας απλός αναλυτικός τύπος για τη γενικά ιδιοδιανύσματα είναι γνωστός. Επιπλέον, τα ιδιοδιανύσματα δεν είναι μοναδικά, επειδή κάθε γραμμικός συνδυασμός των ιδιοδιανυσμάτων για τις ίδιες ιδιοτιμές είναι, επίσης, ένα ιδιοδιάνυσμα για αυτή την ιδιοτιμή. Διάφοροι ερευνητές έχουν προτείνει διάφορες επιλογές των ιδιοδιανυσμάτων, επιλεγμένα για να ικανοποιήσουν χρήσιμες ιδιότητες, όπως η καθετότητα και να έχουν "απλές" μορφές (π. χ., McClellan και Πάρκα, Το 1972, Dickinson και Steiglitz, Το 1982, Grünbaum, Το 1982, Atakishiyev και Wolf, 1997; Candan et al., Το 2000 * Hanna et al., Το 2004 * Gurevich και Hadani, 2008).
Μια απλή προσέγγιση είναι να διακριτοποιήσει μια ιδιοσυνάρτηση του συνεχούς μετασχηματισμού Fourier, των οποίων η πιο γνωστή είναι η συνάρτηση Gauss. Από την περιοδική άθροιση της συνάρτησης που σημαίνει να διακριτοποιηθεί το φάσμα συχνοτήτων και η διακριτοποίηση σημαίνει περιοδική άθροιση του φάσματος, η διακριτοποιημένη και περιοδικά αθροισμένη Γκαουσιανη συνάρτηση αποδίδει ένα ιδιοδιάνυσμα του διακριτού μετασχηματισμού:
- .
- Μία κλειστού τύπου έκφρασης της σειράς δεν είναι γνωστή, αλλά συγκλίνει γρήγορα.
Δύο άλλες κλειστού τύπου αναλυτικά ιδιοδιανύσματα για την ειδική DFT περίοδο N βρέθηκαν από τον Κονγκ, 2008):
Για DFT περίοδο N = 2Λ + 1 = 4Κ +1, όπου K είναι ένας ακέραιος, το ακόλουθο είναι ένα ιδιοδιάνυσμα του DFT:
Για DFT περίοδο N = 2L = 4K, όπου K είναι ένας ακέραιος, το ακόλουθο είναι ένα ιδιοδιάνυσμα του DFT:
Η επιλογή των ιδιοδιανυσμάτων του πίνακα DFT έχει εξελιχθεί σημαντικά κατά τα τελευταία έτη, προκειμένου να καθορίσει ένα φραγμένο και διακριτό μετασχηματισμό Φουριέ —ο πίνακας DFT μπορέι να υψωθεί σε κλασματικές δυνάμεις πολλαπλασιάζοντας τις ιδιοτιμές (π. χ., Rubio και Santhanam, 2005). Ο συνεχής μετασχηματισμός Fourier, οι φυσικές ορθογώνιες ιδιοσυναρτήσεις αποτελούν τα πολυώνυμα Ερμίτ, έτσι ώστε οι διάφορες διακριτές αναλογίες από αυτά να χρησιμοποιηθούν ως ιδιοδιανύσματα του DFT, όπως τα πολυώνυμα Kravchuk (Atakishiyev και Wolf, 1997). Η "καλύτερη" επιλογή των ιδιοδιανυσμάτων για να ορίσετε έναν κλασματικό διακριτό μετασχηματισμό Fourier παραμένει ένα ανοιχτό ερώτημα, όμως.
Η αρχή της αβεβαιότητας[Επεξεργασία | επεξεργασία κώδικα]
Αν η τυχαία μεταβλητή Xk περιορίζεται από
τότε
μπορεί να θεωρηθεί ότι αντιπροσωπεύει μια διακριτή συνάρτηση μάζας πιθανότητας του n, με μια σχετική συνάρτηση μάζας πιθανότητας κατασκευασμένη από τη μετασχηματισμένη μεταβλητή,
Για την περίπτωση των συνεχών συναρτήσεων και , η απροσδιοριστία του Heisenberg δηλώνει ότι
όπου και είναι οι διακυμάνσεις του και , αντίστοιχα, με την ισότητα να επιτυγχάνεται σε περίπτωση κατάλληλα κανονικοποιημένης κατανομής κατά Gauss. Αν και οι αποκλίσεις μπορεί να ορίζονται αναλόγως για το DFT, μια ανάλογη αρχή της αβεβαιότητας δεν είναι χρήσιμη, διότι η αβεβαιότητα δεν θα μετατόπιση-αμετάβλητης. Ακόμα, μια σημαντική αρχή της αβεβαιότητας έχει εισαχθεί από τους Massar και Spindel.[6]
Ωστόσο, η αβεβαιότητα εντροπίας του Hirschman θα έχει μία χρήσιμη αναλογία για την περίπτωση του DFT.[7] Η αρχή της αβεβαιότητας του Hirschman εκφράζεται με την εντροπία Shannon των δύο συναρτήσεων πιθανότητας.
Στην διακριτή περίπτωση, η εντροπίες Shannon ορίζονται ως
και
και η αρχή της αβεβαιότητας εντροπίας γίνεται[7]
Η ισότητα λαμβάνεται για ίσο με μεταφράσεις και διαμορφώσεις ενός κατάλληλα κανονικοποιημένου Kronecker comb της περιόδου , όπου είναι οποιοσδήποτε ακριβής ακέραιος διαιρέτης του .Η συνάρτηση μάζας πιθανότητας τότε θα είναι ανάλογη με ένα κατάλληλα μεταφρασμένο Kronecker comb της περιόδου .[7]
Υπάρχει, επίσης, μία πολύ γνωστή ντετερμινιστική αρχή της αβεβαιότητας που χρησιμοποιεί το σήμα σπανιότητας (ή ο αριθμός των μη μηδενικών συντελεστών).[8] Ας είναι και ο αριθμός των μη μηδενικών στοιχείων των ακολουθιών χρόνου και συχνότητας αντίστοιχα. Τότε,
Ως άμεση συνέπεια της ανισότητας των αριθμητικών και γεωμετρικών μέσων , πρέπει επίσης . Και οι δύο αρχές αβεβαιότητας έδειξαν να είναι σφιχτές για ειδικά επιλεγμένες ακολουθίες-"φράχτη" (διακριτής ώθησης τραίνα), και έχουν πρακτική εφαρμογή για εφαρμογές ανάκτησης σήματος.[8]
Το πραγματικής-εισόδου DFT[Επεξεργασία | επεξεργασία κώδικα]
Αν είναι πραγματικοί αριθμοί, όπως συμβαίνει συχνά σε πρακτικές εφαρμογές τότε το DFT υπακούει στη συμμετρία:
- όπου υποδηλώνει συζυγή μιγαδικό.
Έπεται ότι τα X0 και XN/2 είναι πραγματικοί αριθμοί , και το υπόλοιπο του DFT είναι εντελώς καθορισμένο από ακριβώς N/2-1 μιγαδικούς αριθμούς.
Γενικευμένος DFT (μετατοπισμένη και μη-γραμμική φάση)[Επεξεργασία | επεξεργασία κώδικα]
Είναι δυνατό να μετατοπίσει την δειγματοληψία μετασχηματισμού στο χρόνο και/ή στο πεδίο συχνοτήτων κάποιες πραγματικές μετατοπίσεις α και β, αντίστοιχα. Αυτό είναι μερικές φορές γνωστό ως ένας γενικευμένος DFT (ή GDFT), που ονομάζεται επίσης μετατοπισμένος DFT ή όφσετ DFT, και έχει ανάλογες ιδιότητες με το συνηθισμένο DFT:
Πιο συχνά,χρησιμοποιούνται μετατοπίσεις (μισό δείγμα).Ενώ ο συνήθης DFT αντιστοιχεί σε ένα περιοδικό σήμα τόσο σε χρόνο όσο και στο πεδίο συχνοτήτων , για παράγει ένα σήμα που είναι αντι-περιοδικό στο πεδίο της συχνότητας () και αντίστροφα, για .Έτσι, η συγκεκριμένη περίπτωση είναι γνωστή ως ένας περίεργου χρόνου περίεργης συχνότητας διακριτός μετασχηματισμός Fourier (ή O2DFT).Έτσι οι μετατοπίσεις μετασχηματισμών χρησιμοποιούνται πιο συχνά για συμμετρικά δεδομένα, για να αντιπροσωπεύουν διαφορετικών ορίων συμμετρίες και για πραγματικά συμμετρικά δεδομένα που αντιστοιχούν σε διαφορετικές μορφές του διακριτού μετασχηματισμού συνημιτόνου και ημιτόνου.
Μια άλλη ενδιαφέρουσα επιλογή είναι , η οποία ονομάζεται επίκεντρο DFT (ή CDFT). Το επίκεντρο DFT έχει την χρήσιμη ιδιότητα ότι, όταν το N είναι πολλαπλάσιο του τέσσερα,και οι τέσσερις ιδιοτιμές του (βλ. παραπάνω) έχουν ίσες πολλαπλότητες (Rubio και Santhanam, 2005)[9]
Ο όρος GDFT χρησιμοποιείται επίσης για τη μη-γραμμική φάση των επεκτάσεων του DFT. Ως εκ τούτου,η GDFT μέθοδος παρέχει μια γενίκευση για σταθερού πλάτους ορθογώνιους μετασχηματισμούς μπλοκ συμπεριλαμβανομένων των γραμμικών και μη-γραμμικών τύπων φάσης.Το GDFT είναι ένα πλαίσιο για τη βελτίωση των ιδιοτήτων του χρόνου και του πεδίου της συχνότητας του παραδοσιακού DFT, π. χ. αυτόματη/διασταύρωση-συσχέτιση, με την προσθήκη της κατάλληλα σχεδιασμένης λειτουργίας μορφοποίησης φάσης (μη-γραμμική, σε γενικές γραμμές) στις αρχικές λειτουργίες γραμμικής φάσης (Akansu και Agirman-Tosun, 2010).η[10]
Ο διακριτός μετασχηματισμός Fourier μπορεί να θεωρηθεί ως μια ειδική περίπτωση του μετασχηματισμού-z, με τιμές στον μοναδιαίο κύκλο του μιγαδικού επιπέδου.Περισσότερο γενικοί z-μετασχηματισμοί αντιστοιχούν στις μετατοπίσεις μιγαδικών α και β ανωτέρω.
Πολυδιάστατος DFT[Επεξεργασία | επεξεργασία κώδικα]
Το συνηθισμένο DFT μετατρέπει μια μονοδιάστατη ακολουθία ή σειρά που είναι μια συνάρτηση με ακριβώς μία διακριτή μεταβλητή n. Ο πολυδιάστατος DFT ενός πολυδιάστατου πίνακα που είναι συνάρτηση των d διακριτών μεταβλητών για σε , ορίζεται από:
όπου ως ανωτέρω και το δ δείκτες εξόδου με τιμές από . Αυτό είναι πιο συμπαγώς εκφράσμένο σε διανυσματική μορφή, όπου ορίζουμε και ως d-διαστάσεων διανύσματα των δεικτών από 0 μέχρι , το οποίο ορίζουμε ως :
όπου η διαίρεση ορίζεται ως να είναι ο μετασχηματισμός Φουριέ, και το άθροισμα εκφράζει το σύνολο των ένθετων αθροίσεων παραπάνω.
Το αντίστροφο του πολυδιάστατου DFT , ανάλογα με την μονοδιάστατη περίπτωση, δίνεται από:
Όπως ο μονοδιάστατος DFT εκφράζει την τιμή εισόδου ως υπέρθεση των ημιτονοειδών, ο πολυδιάστατος DFT εκφράζει την τιμή εισόδου ως υπέρθεση των επίπεδων κυμάτων, ή πολυδιάστατα ημιτονοειδή. Η κατεύθυνση της ταλάντωσης στο χώρο είναι . Τα πλάτη είναι . Αυτή η αποσύνθεση είναι μεγάλης σημασίας για τα πάντα, από την ψηφιακή επεξεργασία εικόνας (δύο διαστάσεων) ως την επίλυση μερικών διαφορικών εξισώσεων. Η λύση χωρίζεται σε επίπεδα κύματα.
Ο πολυδιάστατος DFT μπορεί να υπολογιστεί από την σύνθεση μιας ακολουθίας μονοδιάστατων DFTs κατά μήκος κάθε διάστασης. Στη δισδιάστατη περίπτωση η ανεξαρτήτως DFTs των σειρών (δηλαδή, κατά μήκος ), υπολογίζεται πρώτα για να σχηματίσει έναν νέο πίνακα . Στη συνέχεια, η ανεξαρτήτως DFTs του y κατά μήκος των στηλών (κατά μήκος ) υπολογίζεται για να διαμορφώσει το τελικό αποτέλεσμα . Εναλλακτικά, οι στήλες μπορεί να υπολογιστούν πρώτα και στη συνέχεια οι σειρές. Η σειρά δεν έχει σημασία, επειδή οι ένθετες αθροίσεις παραπάνω αντιμετατίθενται.
Ένας αλγόριθμος για τον υπολογισμό ενός μονοδιάστατου DFT είναι συνεπώς επαρκές για τον αποτελεσματικό υπολογισμό ενός πολυδιάστατου DFT. Αυτή η προσέγγιση είναι γνωστή ως αλγόριθμος γραμμή-στήλη. Υπάρχουν επίσης εγγενώς πολυδιάστατοι FFT αλγόριθμοι.
Πραγματικής-εισόδου πολυδιάστατοι DFT[Επεξεργασία | επεξεργασία κώδικα]
Για την εισαγωγή δεδομένων που αποτελούνται από πραγματικούς αριθμούς, το αποτέλεσμα του DFT έχει έναν συζυγή συμμετρικό παρόμοια με την μονοδιάστατη περίπτωση, ανωτέρω:
όπου το αστέρι και πάλι δηλώνει σύνθεση μιγαδικών και ο -ος δείκτης ερμηνεύεται και πάλι με modulo (για ).
Εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]
Ο DFT έχει ευρεία χρήση σε πολλούς τομείς.Εδώ απλά δίνονται μερικά σκίτσα σαν παραδείγματα παρακάτω (βλέπε επίσης τις αναφορές στο τέλος). Όλες οι εφαρμογές του DFT εξαρτώνται σε μεγάλο βαθμό από τη διαθεσιμότητα ενός γρήγορου αλγόριθμου για τον υπολογισμό DFTs και των αντίστροφων,ενός ταχύ μετασχηματισμού Φουριέ.
Φασματική ανάλυση[Επεξεργασία | επεξεργασία κώδικα]
Όταν ο DFT χρησιμοποιείται για σημειακή φασματική ανάλυση, η ακολουθία συνήθως αντιπροσωπεύει ένα πεπερασμένο σύνολο ομοιόμορφα κατανεμημένων χρονικών δειγμάτων κάποιου σήματος , όπου t είναι ο χρόνος. Η μετατροπή από το συνεχή χρόνο σε δείγματα (διακριτός χρόνος) αλλάζει το υποκείμενο μετασχηματισμός Fourier του x(t) σε ένα διακριτού χρόνου μετασχηματισμό Fourier (DTFT), το οποίο συνήθως συνεπάγεται ένα είδος παραμόρφωσης που λέγεται aliasing.Η επιλογή κατάλληλου δείγματος ρυθμού (βλέπε Nyquist rate) είναι το κλειδί για την ελαχιστοποίηση αυτής της στρέβλωσης. Επίσης, η μετατροπή από μία πολύ μεγάλη (ή άπειρη) ακολουθία σε ένα διαχειρίσιμο μέγεθος συνεπάγεται ένα είδος παραμόρφωσης που ονομάζεται διαρροή, η οποία εκδηλώνεται ως απώλεια λεπτομέρειας.κ.α. ψήφισμα) του DTFT. Η επιλογή κατάλληλου μήκους υπο-ακολουθίας είναι το κύριο κλειδί για την ελαχιστοποίηση αυού του αποτελέσματος. Όταν τα διαθέσιμα δεδομένα (και ο χρόνος για να το επεξεργαστεί) είναι περισσότερα από το ποσό που απαιτείται για να επιτευχθεί η επιθυμητή ανάλυση συχνότητας, μια βασική τεχνική είναι να εκτελέσετε πολλούς DFTs, για παράδειγμα, για να δημιουργήσετε ένα φασματογράφημα. Αν το επιθυμητό αποτέλεσμα είναι ένα φάσμα ισχύος και ο θόρυβος ή η τυχαιότητα παρουσιάζονται στα δεδομένα, κατά μέσο όρο το μέγεθος των συστατικών των πολλαπλών DFTs είναι μια χρήσιμη διαδικασία για τη μείωση της διασποράς του φάσματος (που ονομάζεται επίσης ένα περιοδόγραμμα σε αυτό το πλαίσιο) . Δύο παραδείγματα τέτοιων τεχνικών είναι η Welch μέθοδος και η μέθοδος Bartlett, το γενικό αντικείμενο της εκτίμησης του φάσματος ισχύος ενός θορυβώδες σήματος ονομάζεται φασματική εκτίμηση.
Τελική πηγή παραμόρφωσης (ή ίσως την ψευδαίσθηση) είναι ο DFT ο ίδιος, επειδή είναι απλά μια διακριτή δειγματοληψία του DTFT, η οποία είναι μια συνάρτηση συνεχής στο πεδίο της συχνότητας. Αυτό μπορεί να αντιμετωπιστεί με την αύξηση της ανάλυσης του DFT. Η διαδικασία αυτή απεικονίζεται στη Δειγματοληψία του DTFT.
- Η διαδικασία μερικές φορές αναφέρεται ως zero-padding, η οποία είναι μια συγκεκριμένη εφαρμογή που χρησιμοποιείται σε συνδυασμό με τον αλγόριθμο του ταχύ μετασχηματισμού Φουριέ (FFT). Η αναποτελεσματικότητα της εκτέλεσης πολλαπλασιασμών και προσθέσεων με το μηδενικής τιμής "δείγματα" είναι περισσότερη από ότι αντισταθμίζεται από την εγγενή αποτελεσματικότητα του FFT.
- Όπως έχει ήδη σημειωθεί, η διαρροή επιβάλλει ένα όριο για την εγγενή ανάλυση του DTFT. Έτσι, υπάρχει ένα πρακτικό όριο για τα οφέλη που μπορούν να προκύψουν από έναν λεπτόκοκκο DFT.
Φίλτρο τράπεζα[Επεξεργασία | επεξεργασία κώδικα]
Δείτε τράπεζες φίλτρου FFT και Δειγματοληψία του DTFT.
Συμπίεση δεδομένων[Επεξεργασία | επεξεργασία κώδικα]
Το πεδίο της ψηφιακής επεξεργασίας σήματος βασίζεται σε μεγάλο βαθμό σε δραστηριότητες στο πεδίο των συχνοτήτων (για παράδειγμα στον μετασχηματισμό Fourier). Για παράδειγμα, αρκετές μέθοδοι συμπίεσης εικόνας και ήχου με απώλειες απασχολούν τον διακριτό μετασχηματισμό Fourier: το σήμα κόβεται σε μικρά τμήματα , το καθένα είναι μετασχηματισμένο , και τότε οι συντελεστές υψηλής συχνότητας Fourier, οι οποίοι υποτίθεται ότι είναι δυσδιάκριτοι, απορρίπτονται. Το πρόγραμμα αποσυμπίεσης υπολογίζει τον αντίστροφο μετασχηματισμό με βάση αυτό το μειωμένο αριθμό συντελεστών Fourier . (Εφαρμογές συμπίεσης συχνά χρησιμοποιούν μια εξειδικευμένη μορφή του DFT, το διακριτό μετασχηματισμό συνημιτόνου ή μερικές φορές τον τροποποιημένο διακριτό μετασχηματισμό συνημιτόνου.) Κάποιοι σχετικά πρόσφατοι αλγόριθμοι συμπίεσης, ωστόσο, χρησιμοποιούν κυμάτιους μετασχηματισμούς, οι οποίοι δίνουν έναν πιο ομοιόμορφο συμβιβασμό μεταξύ του χρόνου και του πεδίου συχνοτήτων από εκείνους που λαμβάνονται με τεμαχισμό των δεδομένων σε τμήματα και μετασχηματίζοντας κάθε τμήμα. Στην περίπτωση JPEG2000, αυτό αποφεύγει τα ψεύτικα χαρακτηριστικά της εικόνας που εμφανίζονται όταν οι εικόνες είναι εξαιρετικά συμπιεσμένες με το αρχικό JPEG.
Μερικές διαφορικές εξισώσεις[Επεξεργασία | επεξεργασία κώδικα]
Οι διακριτοί μετασχηματισμοί Φουριέ χρησιμοποιούνται συχνά για την επίλυση μερικών διαφορικών εξισώσεων, όπου και πάλι ο DFT χρησιμοποιείται ως προσέγγιση για τη σειρά Fourier (που ανακτάται στο όριο άπειρο N). Το πλεονέκτημα αυτής της προσέγγισης είναι ότι επεκτείνει το σήμα σε εκθετική συνάρτηση μιγαδικών εinx, η οποία είναι ιδιοσυνάρτηση διαφορικών: d/dx einx = σ einx. Έτσι, στην αναπαράσταση Fourier , η παραγώγιση είναι απλή—απλά πολλαπλασιάστε με i n. (Σημειώστε, ωστόσο, ότι η επιλογή του n δεν είναι μοναδική . Για να είναι η μέθοδος συγκλίνουσα, μια επιλογή παρόμοια με εκείνη στο τριγωνομετρικό τμήμα παρεμβολής παραπάνω θα πρέπει να χρησιμοποιείται.) Μια γραμμική διαφορική εξίσωση με σταθερούς συντελεστές μετατρέπεται σε μια εύκολα επιλύσιμη αλγεβρική εξίσωση. Ένα, στη συνέχεια, χρησιμοποιεί το αντίστροφο DFT για να μετατρέψει το αποτέλεσμα πίσω στη κανονική διαστηματική αναπαράσταση. Η προσέγγιση αυτή ονομάζεται φασματική μέθοδος.
Πολλαπλασιασμός πολυωνύμων.[Επεξεργασία | επεξεργασία κώδικα]
Έστω ότι θέλουμε να υπολογίσουμε το γινόμενο πολυώνυμο γ(x) = a(x) · b(x). Η κανονική έκφραση γινομένου για τους συντελεστές του c περιλαμβάνει μια γραμμική (άκυκλη) συνέλιξη, όπου οι δείκτες δεν "εκτυλίσσονται γύρω". Αυτό μπορεί να ξαναγραφεί ως μια κυκλική συνέλιξη παίρνοντας τους διανυσματικούς συντελεστές για a(x) και b(x) με το σταθερό όρο πρώτα, μετά την προσάρτηση μηδενικών έτσι ώστε οι διανυσματικοί συντελεστές a και b που προκύπτον να έχουν διάσταση d > deg(a(x)) + deg(b(x)). Στη συνέχεια,
Όπου c είναι το διάνυσμα των συντελεστών του c(x), και η πράξη συνέλιξη ορίζεται έτσι
Αλλά η συνέλιξη γίνεται πολλαπλασιασμός μέσω του DFT:
Εδώ το γινόμενο διανυσμάτων προκύπτει στοιχειωδώς. Έτσι, οι συντελεστές του πολυωνυμικού γινομένου c(x) είναι οι όροι 0, ..., deg(a(x)) + deg(b(x)) του συντελεστή διάνυσμα
Με έναν ταχύ μετασχηματισμό Φουριέ, ο αλγόριθμος που προκύπτει παίρνει Ο (N log N) αριθμητικές πράξεις. Λόγω της απλότητας και της ταχύτητας, ο Couley-Tukey ΤΜΦ αλγόριθμος , ο οποίος περιορίζεται σε σύνθετα μεγέθη, συχνά επιλέγεται για το πράξη του μετασχηματισμού . Σε αυτή την περίπτωση, το d θα πρέπει να επιλέγεται ως ο μικρότερος ακέραιος που είναι μεγαλύτερος από το άθροισμα των εισόδων βαθμών πολυωνύμων που είναι παραγωγίσιμοι στις πρώτες παραγώγους (π. χ. 2, 3, και 5, ανάλογα με την υλοποίηση FFT).
Πολλαπλασιασμός μεγάλων ακεραίων[Επεξεργασία | επεξεργασία κώδικα]
Ο πιο γρήγορος γνωστός αλγόριθμος για τον πολλαπλασιασμό των πολύ μεγάλων ακεραίων χρησιμοποιεί την μέθοδο πολλαπλασιασμού πολυωνύμων που περιγράφεται παραπάνω.Οι ακέραιοι μπορούν να αντιμετωπιστεί ως η τιμή ενός πολυωνύμου δίνοντας τιμή ειδικά στον αριθμό της βάσης, με τους συντελεστές του πολυωνύμου να αντιστοιχούν στα ψηφία σε αυτή τη βάση. Μετά τον πολλαπλασιασμό πολυωνύμων ,ένα βήμα σχετικά χαμηλής πολυπλοκότητας μεταφοράς-διάδοσης ολοκληρώνει τον πολλαπλασιασμό.
Συνέλιξη[Επεξεργασία | επεξεργασία κώδικα]
Όταν τα δεδομένα έχουν συνελιχθεί με μια συνάρτηση με μεγάλη υποστήριξη, όπως για υποδειγματοληψία από ένα μεγάλο λόγο δειγματοληψίας, εξαιτίας του θεωρήματος Συνέλιξης και του αλγορίθμου FFT, μπορεί να είναι πιο γρήγορη για να το μετασχηματίσει, να πολλαπλασιάσετε σημειακά από το μετασχηματισμό του φίλτρου και στη συνέχεια να μετασχηματιστεί αντίστροφα. Εναλλακτικά, ένα καλό φίλτρο επιτυγχάνεται απλώς με την περικοπή των μετασχηματισμών δεδομένων και του εκ νέου μετασχηματισμού του συντομευμένου συνόλου δεδομένων.
Κάποια διακριτός μετασχηματισμός Fourier ζεύγη[Επεξεργασία | επεξεργασία κώδικα]
| Note | ||
|---|---|---|
| Shift theorem | ||
| Real DFT | ||
| from the geometric progression formula | ||
| from the binomial theorem | ||
| is a rectangular window function of W points centered on n=0, where W is an odd integer, and is a sinc-like function (specifically, is a Dirichlet kernel) | ||
| Discretization and periodic summation of the scaled Gaussian functions for . Since either or is larger than one and thus warrants fast convergence of one of the two series, for large you may choose to compute the frequency spectrum and convert to the time domain using the discrete Fourier transform. |
Γενικεύσεις[Επεξεργασία | επεξεργασία κώδικα]
Εκπροσώπηση θεωρίας[Επεξεργασία | επεξεργασία κώδικα]
(Για περισσότερες λεπτομέρειες σε αυτό το θέμα,δείτε θεωρία αναπαράστασης των πεπερασμένων ομάδων και διακριτός μετασχηματισμός Φουριέ)
Ο DFT μπορεί να ερμηνευθεί ως η μιγαδική τιμή θεωρίας αναπαράστασης της πεπερασμένης κυκλικής ομάδας. Με άλλα λόγια, μια ακολουθία από n μιγαδικούς αριθμούς μπορεί να θεωρηθεί ως ένα στοιχείο του n-διάστατου χώρου μιγαδικών Cn ή αντίστοιχα μια συνάρτηση f από την πεπερασμένη κυκλική ομάδα τάξης n στους μιγαδικούς αριθμούς, το Zn → C. Οπότε η f είναι μια συνάρτηση κλάσης σχετικά με την πεπερασμένη κυκλική ομάδα, και έτσι μπορεί να εκφραστεί ως γραμμικός συνδυασμός των αμείωτων χαρακτήρων αυτής της ομάδας, που είναι οι ρίζες της ενότητας.
Από αυτή την άποψη, μπορεί κανείς να γενικεύσει τον DFT για την εκπροσώπηση θεωρίας γενικά, ή πιο ειδικά για την θεωρία αναπαράστασης των πεπερασμένων ομάδων.
Ακόμα πιο συγκεκριμένα, μπορεί κανείς να γενικεύσει το DFT είτε αλλάζοντας τον στόχο (παίρνει τιμές σε ένα πεδίο, εκτός από το μιγαδικοί αριθμοί), ή το πεδίο τιμών (ομάδα άλλη από μια πεπερασμένη κυκλική ομάδα), όπως περιγράφεται στη συνέχεια.
Άλλα πεδία[Επεξεργασία | επεξεργασία κώδικα]
Πολλές από τις ιδιότητες του DFT εξαρτώνται μόνο από το γεγονός ότι είναι μια πρωτόγονη ρίζα της ενότητας, μερικές φορές συμβολίζεται με ή (έτσι ώστε ). Αυτές οι ιδιότητες περιλαμβάνουν την πληρότητα, την καθετότητα, Plancherel/Parseval, περιοδικότητα, αλλαγή, συνέλιξη, και μεμονομένες ιδιότητες παραπάνω, καθώς και πολλούς FFT αλγόριθμους. Για το λόγο αυτό, ο διακριτός μετασχηματισμός Fourier μπορεί να οριστεί χρησιμοποιώντας ρίζες της ενότητας σε πεδία άλλα από των μιγαδικών αριθμών, και τέτοιες γενικεύσεις είναι κοινώς γνωστές ως αριθμιτική-θεωρητικοί μετασχηματισμοί (NTTs) στην περίπτωση των πεπερασμένων πεδίων. Για περισσότερες πληροφορίες, δείτε τον αριθμητικό-θεωρητικό μετασχηματισμό και τον διακριτό μετασχηματισμό Φουριέ (γενικά).
Άλλα πεπερασμένα σύνολα[Επεξεργασία | επεξεργασία κώδικα]
Το πρότυπο DFT δρα σε μια ακολουθία x0, x1, ..., xN−1 μιγαδικών αριθμών, η οποία μπορεί να θεωρηθεί ως μια συνάρτηση {0, 1, ..., N − 1} → C. Η πολυδιάστατη DFT δρα σε πολυδιάστατες ακολουθίες, οι οποίες μπορούν να θεωρηθούν ως συναρτήσεις
Αυτό υποδηλώνει την γενίκευση σε μετασχηματισμούς Fourier σε αυθαίρετα πεπερασμένα σύνολα, που δρουν σε συναρτήσεις G → C , όπου η G είναι μια πεπερασμένο σύνολο. Σε αυτό το πλαίσιο, το πρότυπο DFT είναι ο μετασχηματισμός Fourier σε μια κυκλική ομάδα, ενώ η πολυδιάστατη DFT είναι ένας μετασχηματισμός Φουριέ σε άμεσο άθροισμα των κυκλικών ομάδων.
Εναλλακτικές λύσεις[Επεξεργασία | επεξεργασία κώδικα]
Υπάρχουν διάφορες εναλλακτικές λύσεις για τον DFT για διάφορες εφαρμογές, εξέχουσα μεταξύ των οποίων είναι τα κύματα. Το αναλογικό του DFT είναι ο διακριτός μετασχηματισμός κυμάτων (DWT). Από την άποψη της ανάλυσης χρόνου-συχνότητας, ένας βασικός περιορισμός του μετασχηματισμού Φουριέ είναι ότι δεν περιλαμβάνει πληροφορίες θέσης, μόνο συχνότητας πληροφορίες, και έτσι έχει δυσκολία στην εκπροσώπηση μεταβατικών φαινομένων. Επειδή τα κύματα έχουν θέση καθώς και συχνότητα, είναι σε θέση να αντιπροσωπεύουν καλύτερα τοποθεσία, σε βάρος της μεγαλύτερης δυσκολίας να αντιπροσωπεύει τη συχνότητα. Για λεπτομέρειες, ανατρέξτε στη σύγκριση του διακριτού μετασχηματισμού κυμάτων με το διακριτό μετασχηματισμό Φουριέ.
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ As a linear transformation on a finite-dimensional vector space, the DFT expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the Xk can thus be viewed as coefficients of x in an orthonormal basis.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Strang, Gilbert (May–June 1994). «Wavelets». American Scientist 82 (3): 253. http://www.jstor.org/stable/29775194. Ανακτήθηκε στις 8 October 2013. «This is the most important numerical algorithm of our lifetime...».
- ↑ Sahidullah, Md.; Saha, Goutam (Feb 2013). «A Novel Windowing Technique for Efficient Computation of MFCC for Speaker Recognition». IEEE Signal Processing Letters 20 (2): 149–152. doi:. Bibcode: 2013ISPL...20..149S. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6387265&isnumber=6380557.
- ↑ Cooley et al., 1969
- ↑ «Shift zero-frequency component to center of spectrum – MATLAB fftshift». http://www.mathworks.com/. Natick, MA 01760: The MathWorks, Inc. Ανακτήθηκε στις 10 Μαρτίου 2014. Εξωτερικός σύνδεσμος στο
|work=(βοήθεια) - ↑ T. G. Stockham, Jr., "High-speed convolution and correlation," in 1966 Proc.
- ↑ Massar, S.; Spindel, P. (2008). «Uncertainty Relation for the Discrete Fourier Transform». Physical Review Letters 100 (19). doi:. Bibcode: 2008PhRvL.100s0401M.
- ↑ 7,0 7,1 7,2 DeBrunner, Victor; Havlicek, Joseph P.; Przebinda, Tomasz; Özaydin, Murad (2005). «Entropy-Based Uncertainty Measures for , and With a Hirschman Optimal Transform for ». IEEE Transactions on Signal Processing 53 (8): 2690. doi:. Bibcode: 2005ITSP...53.2690D. http://redwood.berkeley.edu/w/images/9/95/2002-26.pdf. Ανακτήθηκε στις 2011-06-23.
- ↑ 8,0 8,1 Donoho, D.L.; Stark, P.B (1989). «Uncertainty principles and signal recovery». SIAM Journal on Applied Mathematics 49 (3): 906–931. doi:.
- ↑ Santhanam, Balu; Santhanam, Thalanayar S. "Discrete Gauss-Hermite functions and eigenvectors of the centered discrete Fourier transform"[νεκρός σύνδεσμος], Proceedings of the 32nd IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2007, SPTM-P12.4), vol.
- ↑ Akansu, Ali N.; Agirman-Tosun, Handan "Generalized Discrete Fourier Transform With Nonlinear Phase", IEEE Transactions on Signal Processing, vol. 58, no. 9, pp. 4547-4556, Sept. 2010.
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- Brigham, E. Oran (1988). The fast Fourier transform and its applications. Englewood Cliffs, N.J.: Prentice Hall. ISBN 0-13-307505-2.
- Oppenheim, Alan V.· Schafer, R. W.· Buck, J. R. (1999). Discrete-time signal processing
 . Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2.
. Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2. - Smith, Steven W. (1999). «Chapter 8: The Discrete Fourier Transform». The Scientist and Engineer's Guide to Digital Signal Processing (Second έκδοση). San Diego, Calif.: California Technical Publishing. ISBN 0-9660176-3-3.
- Cormen, Thomas H.· Charles E. Leiserson· Ronald L. Rivest· Clifford Stein (2001). «Chapter 30: Polynomials and the FFT». Introduction to Algorithms (Second έκδοση). MIT Press and McGraw-Hill. σελίδες 822–848. ISBN 0-262-03293-7. esp. section 30.2: The DFT and FFT, pp. 830–838.
- P. Duhamel; B. Piron; J. M. Etcheto (1988). «On computing the inverse DFT». IEEE Trans. Acoust., Speech and Sig. Processing 36 (2): 285–286. doi:.
- J. H. McClellan; T. W. Parks (1972). «Eigenvalues and eigenvectors of the discrete Fourier transformation». IEEE Trans. Audio Electroacoust. 20 (1): 66–74. doi:.
- Bradley W. Dickinson; Kenneth Steiglitz (1982). «Eigenvectors and functions of the discrete Fourier transform». IEEE Trans. Acoust., Speech and Sig. Processing 30 (1): 25–31. doi:. (Note that this paper has an apparent typo in its table of the eigenvalue multiplicities: the +i/−i columns are interchanged. The correct table can be found in McClellan and Parks, 1972, and is easily confirmed numerically.)
- F. A. Grünbaum (1982). «The eigenvectors of the discrete Fourier transform». J. Math. Anal. Appl. 88 (2): 355–363. doi:.
- Natig M. Atakishiyev; Kurt Bernardo Wolf (1997). «Fractional Fourier-Kravchuk transform». J. Opt. Soc. Am. A 14 (7): 1467–1477. doi:. Bibcode: 1997JOSAA..14.1467A.
- C. Candan; M. A. Kutay; H. M.Ozaktas (2000). «The discrete fractional Fourier transform». IEEE Trans. on Signal Processing 48 (5): 1329–1337. doi:. Bibcode: 2000ITSP...48.1329C.
- Magdy Tawfik Hanna; Nabila Philip Attalla Seif; Waleed Abd El Maguid Ahmed (2004). «Hermite-Gaussian-like eigenvectors of the discrete Fourier transform matrix based on the singular-value decomposition of its orthogonal projection matrices». IEEE Trans. Circ. Syst. I 51 (11): 2245–2254. doi:.
- Shamgar Gurevich; Ronny Hadani (2009). «On the diagonalization of the discrete Fourier transform». Applied and Computational Harmonic Analysis 27 (1): 87–99. doi:. preprint at.
- Shamgar Gurevich; Ronny Hadani; Nir Sochen (2008). «The finite harmonic oscillator and its applications to sequences, communication and radar». IEEE Transactions on Information Theory 54 (9): 4239–4253. doi:. preprint at.
- Juan G. Vargas-Rubio; Balu Santhanam (2005). «On the multiangle centered discrete fractional Fourier transform». IEEE Sig. Proc. Lett. 12 (4): 273–276. doi:. Bibcode: 2005ISPL...12..273V.
- J. Cooley; P. Lewis; P. Welch (1969). «The finite Fourier transform». IEEE Trans. Audio Electroacoustics 17 (2): 77–85. doi:.
- F.N. Kong (2008). «Analytic Expressions of Two Discrete Hermite-Gaussian Signals». IEEE Trans. Circuits and Systems –II: Express Briefs. 55 (1): 56–60. doi:.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Διαδραστική εξήγηση του DFT
- Matlab tutorial για το Διακριτό Μετασχηματισμό Fourier Αρχειοθετήθηκε 2016-03-04 στο Wayback Machine.
- Interactive flash tutorial για το DFT
- Τα μαθηματικά της Διακριτός Μετασχηματισμός Fourier από τον ιούλιο. O. Smith III
- FFTW: η Γρήγορη υλοποίηση του DFT - κωδικοποιημένα σε C και κάτω από τη Γενική Άδεια Δημόσιας χρήσης (GPL)
- Γενικού Σκοπού FFT Συσκευασία: ένα Ακόμη γρήγορο DFT υλοποίηση σε C & FORTRAN, ανεκτική άδεια
- Επεξήγηση: Ο Διακριτός Μετασχηματισμός Fourier






![{\displaystyle \scriptstyle n\ \in \ [0,\ N-1],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d186a6f8dde39986516e78d6db0cbea53649a7e0)








![{\displaystyle u_{k}=\left[e^{{\frac {2\pi i}{N}}kn}\;|\;n=0,1,\ldots ,N-1\right]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b25ad6ebc181a35d3b71ed8dac3cb5ced6dd6bf)



























![{\displaystyle p(t)={\frac {1}{N}}\left[X_{0}+X_{1}e^{2\pi it}+\cdots +X_{N/2-1}e^{(N/2-1)2\pi it}+X_{N/2}\cos(N\pi t)+X_{N/2+1}e^{(-N/2+1)2\pi it}+\cdots +X_{N-1}e^{-2\pi it}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8eff8aee2c25106dc630a9c074751505c0faf9f)
![{\displaystyle p(t)={\frac {1}{N}}\left[X_{0}+X_{1}e^{2\pi it}+\cdots +X_{\lfloor N/2\rfloor }e^{\lfloor N/2\rfloor 2\pi it}+X_{\lfloor N/2\rfloor +1}e^{-\lfloor N/2\rfloor 2\pi it}+\cdots +X_{N-1}e^{-2\pi it}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/17c0fe2e679692d040e9edc35976a6791eecab82)













































![{\displaystyle F(m)=\prod _{s=K+1}^{L}\left[\cos \left({\frac {2\pi }{N}}m\right)-\cos \left({\frac {2\pi }{N}}s\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/452500005f28e338188d3008d9c99760f2b290ae)
![{\displaystyle F(m)=\sin \left({\frac {2\pi }{N}}m\right)\prod _{s=K+1}^{L-1}\left[\cos \left({\frac {2\pi }{N}}m\right)-\cos \left({\frac {2\pi }{N}}s\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7090fae53ffec58d0ebcbcfc4dc74b70e110ac30)




























































































