Ακέραιος αριθμός

Αριθμιτική

Ταξινόμηση
Dewey	513
MSC2010	97Fxx

Ακέραιοι ονομάζονται όλοι οι φυσικοί αριθμοί μαζί με τους αντίθετους τους και το μηδέν. Το σύνολο των ακεραίων δηλαδή το σύνολο:

$\mathbb{Z}=\{0,\pm1,\pm2,...\}$

συμβολίζεται με το γράμμα $\mathbb{Z}$, αρχικό της λέξης Zahlen που στα γερμανικά σημαίνει αριθμός.

Το σύνολο $\mathbb{Z}$ ορίζεται επίσης ως εξής:

$\mathbb{Z}=\{x-y:x,y\in\mathbb{N}\}$

.

Όπως και το σύνολο των φυσικών, το σύνολο των ακεραίων είναι άπειρο αριθμήσιμο με πληθάριθμο $\aleph_0$ (άλεφ-μηδέν).

Αλγεβρικές Ιδιότητες

Οι ακέραιοι αριθμοί αποτελούν αντιμεταθετικό δακτύλιο ως προς την πρόσθεση και τον πολλαπλασιασμό. Το άθροισμα και το γινόμενο δυο ακεραίων είναι δηλαδή και αυτό ακέραιος. Ισχύουν η αντιμεταθετική και προσετεριστική ιδιότητα ως προς προσθεση και πολλαπλασιασμο και ο πολλαπλασιασμός είναι επιμεριστικός ως προς την πρόσθεση.

Οι ακέραιοι αριθμοί δεν αποτελούν σώμα. Ο αντίστοφος ενός ακεραίου ως προς τον πολλαπλασιασμό δεν είναι δηλαδη απαραίτητα ακέραιος. Το μικρότερο σώμα που περιέχει τους ακεραίους είναι οι ρητοί αριθμοί.

Πρόσθεση	Πολλαπλασιασμός
$a+b\in\mathbb{Z}$	$a\times b\in\mathbb{Z}$	σύνολο κλειστό ως προς τις πράξεις
$a+b=b+a\,$	$a\times b=b\times a$	αντιμεταθετική ιδιότητα
$a+(b+c)=(a+b)+c\,$	$a\times (b\times c)=(a\times b)\times c$	προσεταιριστική ιδιότητα
$a+0=a\,$	$a\times 1=a$	ουδέτερο στοιχείο
$a+(-a)=0\,$	δεν υπάρχει	αντίθετο στοιχείο
$a\times(b+c)=(a\times b) + (a\times c)$		επιμεριστική ιδιότητα

Διάταξη

Οι ακέραιοι αποτελούν ένα γνησίως διατεταγμένο σύνολο:

$... < -2 < -1 < 0 < 1 < 2 < ...$

Οι ακέραιοι αποτελούν επομένως ένα διατεταγμένο δακτύλιο.

Κατασκευή

Οι διακεκομένες μπλε γραμμές συνδεουν τα ισοδύναμα ζευγη.

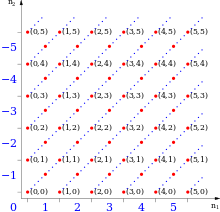
Το σύνολο των ακεραίων μπορεί να κατασκευαστεί από τους φυσικούς αριθμούς.

Θεωρούμε το σύνολο $\mathbb{N} \times \mathbb{N}$ των ζευγαριών των φυσικών αριθμών και ορίζουμε την ακόλουθη σχέση ισοδυναμίας:

$(a, b) \sim (c, d) \Leftrightarrow a + d = c + b.$

Το σύνολο των κλάσεων ισοδυναμίας $\mathbb{N} \times \mathbb{N} \,/\! \sim$ ορίζει τους φυσικούς αριθμούς $\mathbb{Z}$. Την κλάση ισοδυναμίας του ζεύγους $(a, b)$ τη συμβολίζουμε με $[(a, b)]$ ή $a- b$. Έτσι στην κλάση ισοδυναμίας π.χ. του 0 ανήκουν τα μεταξύ τους ισοδύναμα ζεύγη (1,1), (2,2),... .

Ένας ακέραιος αριθμός $(a, b)$ είναι θετικός, όταν $a > b$, αρνητικός όταν $a < b$ και 0 όταν $a = b$. Κάθε ακέραιος είναι ισοδύναμος με έναν της μορφής (n,0), (0,n) ή (0,0), ο οποίος διαλεγεται συνήθως και ως αντιπρόσωπος της αντίστοιχης κλάσης.

Η πρόσθεση και ο πολλαπλασιασμός μπορούν να οριστούν αντίστοιχα με τις πράξεις στους φυσικούς αριθμούς:

$[(a,b)]+[(c,d)] = [(a+c,b+d)].\,$

$[(a,b)]\cdot[(c,d)] = [(ac+bd,ad+bc)].\,$

Το αντίστροφο (ως προς την πρόσθεση) στοιχείο προκύπτει από την αναστροφή της σειράς των όρων του ζευγους:

$-[(a,b)] = [(b,a)].\,$

Η συνήθης διάταξη δίνεται από τη σχέση:

$[(a,b)]<[(c,d)] \Leftrightarrow a+d < b+c.\,$

Πληθάριθμος

Το σύνολο των ακεραίων έχει πληθάριθμο $\aleph_0$ (άλεφ-μηδέν), όπως και το σύνολο των φυσικών. Αυτό αποδεικνύεται από την ύπάρξη αμφιμονότιμης και επί συνάρτησης $f:\mathbb{Z}\to \mathbb{N}$, σύναρτησης δηλαδή που κάθε στοιχείο των φυσικών αριθμών είναι μια αντιστοιχιση από ένα ακριβώς στοιχείο των ακεραίων:

$f(x) = \begin{cases} 2|x|, & x < 0 \\ 2x+1, & x \ge 0. \end{cases}$

Δείτε επίσης

Σύνολο των

• φυσικών αριθμών $\N$
• ρητών αριθμών $\Q$
• πραγματικών αριθμών $\R$
• μιγαδικών αριθμών $\C$.