Σειρές Φουριέ
Στα μαθηματικά, μια σειρά Fourier (σειρά Φουριέ - αγγλική προφορά: / fɔərieɪ /) είναι ένας τρόπος για να περιγραφεί ένα κύμα που μοιάζει να λειτουργεί ως ένας συνδυασμός απλών ημιτονοειδών κυμάτων. Πιο επίσημα, αποσυνθέτει κάθε περιοδική συνάρτηση ή περιοδικό σήμα στο άθροισμα (ενδεχομένως άπειρο) ενός συνόλου απλών συναρτήσεων ταλάντωσης, δηλαδή ημίτονων και συνημίτονων (ή σύνθεση εκθετικών). Ο μετασχηματισμός Fourier διακριτού χρόνου είναι μία περιοδική συνάρτηση, που συχνά ορίζεται από τους όρους μιας σειράς Fourier. Επιπλέον, ο μετασχηματισμός-Ζ μετατρέπεται σε σειρά Fourier με την προϋπόθεση ότι |z|=1. Οι σειρές Fourier, επίσης, βασίζονται στην αρχική απόδειξη του θεωρήματος δειγματοληψίας του Nyquist–Shannon. Είναι ένα ιδιαίτερα χρήσιμο εργαλείο του Λογισμού που βρίσκει πολλές εφαρμογές σε διάφορα πεδία της επιστήμης, π.χ. στις χρονολογικές σειρές στην στατιστική, στην ανάλυση σήματος και εικόνας, στην οικονομετρία, την μηχανική κλπ.
|
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Η σειρά Fourier πήρε το όνομά της προς τιμήν του Ζοζέφ Φουριέ (Jean-Baptiste Joseph Fourier (1768-1830)), ο οποίος έκανε σημαντικές συνεισφορές στη μελέτη των τριγωνομετρικών σειρών, μετά από προκαταρκτικές έρευνες από τον Λέοναρντ Όιλερ, Ζαν λε Ροντ ντ' Αλαμπέρ, και Ντάνιελ Μπερνούλι..[nb 1] Ο Fourier εισήγαγε τη σειρά με σκοπό την επίλυση της εξίσωσης της θερμότητας σε μια μεταλλική πλάκα, δημοσιεύοντας τα πρώτα αποτελέσματα του το 1807 Mémoire sur la propagation de la chaleur dans les corps solides (Διατριβή στην διάδοση της θερμότητας σε στερεά σώματα), και με την δημοσίευση Théorie analytique de la chaleur (Αναλυτική Θεωρία της Θερμότητας) το 1822. Η πρώτη ιδέα για την αποσύνθεση μιας περιοδικής συνάρτησης σε άθροισμα απλών συναρτήσεων ταλάντωσης, που χρονολογείται περίπου τον 3ο αιώνα π.Χ., όπου οι αρχαίοι αστρονόμοι πρότειναν ένα εμπειρικό μοντέλο πλανητικών κινήσεων, στηριζόμενο στην κυκλική τροχιά.
Η εξίσωση θερμότητας είναι μια μερική διαφορική εξίσωση. Πριν από το έργο του Fourier, καμία λύση για την εξίσωση της θερμότητας δεν ήταν γνωστή στη γενική περίπτωση, αν και ήταν γνωστές οι μερικές λύσεις της στην περίπτωση που η πηγή θερμότητας συμπεριφερόταν με έναν απλό τρόπο, ιδίως, εάν η πηγή θερμότητας ήταν ένα ημιτονοειδές ή συνημιτονοειδές κύμα. Αυτές οι μερικές λύσεις καλούνται χαρακτηριστικές συναρτήσεις ή ιδιοσυναρτήσεις. Η ιδέα του Fourier ήταν να μοντελοποιήσει μια περίπλοκη πηγή θερμότητας ως μια επαλληλία (ή γραμμικό συνδυασμό) απλών ημιτονοειδών και συνημιτονοειδών κυμάτων, και να γράψει τη λύση ως μια επαλληλία των αντίστοιχων ιδιοσυναρτήσεων. Η σύνθεση των μελών της επαλληλίας ή του γραμμικού συνδυασμού ονομάζεται σειρά Fourier.
Από μια σύγχρονη άποψη, τα αποτελέσματα του Fourier είναι κάπως άτυπα, καθώς δεν υπήρχε ακριβής ορισμός των εννοιών της συνάρτησης και του ολοκληρώματος στις αρχές του δέκατου ένατου αιώνα. Αργότερα, οι Peter Gustav Lejeune Dirichlet[1] και Μπέρναρντ Ρίμαν[2][3][4] εξέφρασαν τα αποτελέσματα του Fourier με μεγαλύτερη ακρίβεια και τυπικότητα.
Αν και ο πρωταρχικός στόχος ήταν η επίλυση της εξίσωσης θερμότητας, αργότερα έγινε φανερό ότι οι ίδιες τεχνικές μπορούν να εφαρμοστούν σε ένα ευρύ φάσμα προβλημάτων μαθηματικών και φυσικής, και ιδιαίτερα προβλήματα που αφορούν γραμμικές διαφορικές εξισώσεις με σταθερούς συντελεστές, για τις οποίες οι ιδιοσυναρτήσεις είναι ημιτονοειδών μορφών. Η σειρά Fourier έχει πολλές τέτοιες εφαρμογές στον τομέα της ηλεκτρολογίας, της ανάλυσης κραδασμών, στην ακουστική, οπτική, επεξεργασία σήματος, επεξεργασία εικόνας, στην κβαντομηχανική, οικονομετρία,[5] στη θεωρία λεπτού κέλυφους με τοιχώματα,[6] κ.τ.λ.
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Σε αυτή την ενότητα, s (x) είναι μια συνάρτηση της πραγματικής μεταβλητής x, ολοκληρώσιμη στο διάστημα , για πραγματικούς αριθμούς και P. Εμείς θα προσπαθήσουμε να αναπαραστήσουμε το s σε αυτό το διάστημα ως άθροισμα άπειρων, δηλαδή σειρά, αρμονικών συναρτήσεων. Έξω από το διάστημα, η σειρά είναι περιοδική με περίοδο P (συχνότητα 1 / P). Επομένως, αν s έχει επίσης αυτή την ιδιότητα, η προσέγγιση ισχύει σε ολόκληρη την ευθεία των πραγματικών αριθμών. Μπορούμε να ξεκινήσουμε με ένα πεπερασμένο άθροισμα (ή μερικό άθροισμα):
- για ακεραίους
είναι μία περιοδική συνάρτηση με περίοδο P. Χρησιμοποιώντας τις ταυτότητες :

μπορούμε επίσης να γράψουμε τη συνάρτηση στις παρακάτω ισοδύναμες μορφές:
όπου:
Οι συντελεστές (γνωστοί ως συντελεστές Fourier ) υπολογίζονται ως εξής:[7]
προσεγγίζει την στο διάστημα και η προσέγγιση βελτιώνεται καθώς N → ∞. Το άθροισμα άπειρων όρων, καλείται σειρά Fourier που αναπαριστά το . Σε μηχανολογικές εφαρμογές, η σειρά Fourier γενικά θεωρείται ότι συγκλίνει παντού εκτός από τα σημεία ασυνέχειας, δεδομένου ότι οι συναρτήσεις που χρησιμοποιούνται στη μηχανική είναι πιο καλά ορισμένες από αυτές που οι μαθηματικοί μπορούν να παρέχουν ως αντι-παραδείγματα σε αυτό το τεκμήριο. Ειδικότερα, η σειρά Fourier συγκλίνει απόλυτα και ομοιόμορφα σε s (x) όταν η παράγωγος του s (x) (η οποία δεν μπορεί να ορίζεται παντού) είναι ολοκληρώσιμο τετράγωνο.[8] Αν μια συνάρτηση είναι τετράγωνο-ολοκληρώσιμη στο διάστημα , τότε η σειρά Fourier συγκλίνει στη συνάρτηση σχεδόν σε κάθε σημείο. Δείτε σύγκλιση σειρών Fourier. Είναι δυνατόν να καθοριστούν οι συντελεστές Fourier για γενικότερες συναρτήσεις ή κατανομές, σε τέτοιες περιπτώσεις, η σύγκλιση στο πρότυπο ή ασθενής σύγκλιση είναι συνήθως αξιοσημείωτη.
-
Μια άλλη απεικόνιση της προσέγγισης του ενός τετραγωνικού κύματος με τη λήψη των πρώτων 1, 2, 3 και 4 από τους όρους της σειράς Fourier
-
Μια απεικόνιση της προσέγγισης του πριονωτού κύματος του ίδιου πλάτους και συχνότητας για σύγκριση
Παράδειγμα 1: μια απλή σειρά Fourier[Επεξεργασία | επεξεργασία κώδικα]


Χρησιμοποιούμε τον παραπάνω τύπο για να επεκτείνουμε μια σειρά Fourier μιας πολύ απλής συνάρτησης. Σκεφτείτε ένα πριονωτό κύμα
Στην περίπτωση αυτή, οι συντελεστές Fourier δίνονται από
Μπορεί να αποδειχθεί ότι η σειρά Fourier συγκλίνει στο s (x) σε κάθε σημείο x όπου α είναι διαφορίσιμη, και ως εκ τούτου: :
-
()
Όταν x = π, η σειρά Fourier συγκλίνει στο 0, η οποία είναι το μισό άθροισμα στο αριστερό και το δεξί όριο του s στο x = π. Αυτή είναι μια ιδιαίτερη περίπτωση του θεωρήματος Dirichlet για την σειρά Fourier .

Το παρακάτω παράδειγμα μας οδηγεί στην λύση του προβλήματος Basel.
Παράδειγμα 2: Το κίνητρο του Fourier[Επεξεργασία | επεξεργασία κώδικα]
Η επέκταση της σειράς Fourier στη συνάρτηση του 1ου παραδείγματος μοιάζει αρκετά πιο περίπλοκο από τον τύπο s(x) = x/π, και δεν είναι ακριβώς εμφανές γιατί χρειαζόμαστε αυτή τη σειρά Fourier. Ενώ υπάρχουν αρκετές εφαρμογές, εμείς εμμένουμε στο κίνητρο του Fourier για την επίλυση της εξίσωσης της θερμότητας. Για παράδειγμα, ας θεωρήσουμε μια μεταλλική πλάκα σε σχήμα τετραγώνου με μήκος πλευράς π μέτρα, με συντεταγμένες (x, y) ∈ [0, π] × [0, π]. Αν δεν υπάρχει πηγή θερμότητας εντός της πλάκας, και αν 3 από τις 4 πλευρές διατηρούνται στους 0 βαθμούς Κελσίου, ενώ η τέταρτη πλευρά, με αρχική τιμή y = π, διατηρείται στη θερμοκρασιακή βαθμίδα T(x, π) = x βαθμούς Κελσίου, για x στο (0, π), τότε μπορεί κανείς να αποδείξει ότι η στάσιμη κατανομή της θερμότητας (ή η κατανομή της θερμότητας μετά από μια μακροχρόνια περίοδο έχει παρέλθει) δίνεται ως εξής:
Όπου, sinh είναι η υπερβολική ημιτονοειδής συνάρτηση. Αυτή η λύση της εξίσωσης της θερμότητας προκύπτει από τον πολλαπλασιασμό κάθε όρου του Eq.1 με sinh(ny)/sinh(nπ). Ενώ στο παράδειγμά μας η συνάρτηση s(x) φαίνεται να έχει μια άσκοπα περίπλοκη σειρά Fourier, η κατανομή της θερμότητας T(x, y) είναι τετριμμένη. Η συνάρτηση T δεν μπορεί να γραφεί ως έκφραση κλειστής μορφής. Η μέθοδος επίλυσης του προβλήματος της θερμότητας κατασκευάστηκε πιθανόν από το έργο του Fourier.
Άλλες εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]
Μια άλλη εφαρμογή των σειρών Fourier είναι η επίλυση του προβλήματος Basel χρησιμοποιώντας το θεώρημα Parseval. Το παράδειγμα γενικεύεται και μπορεί κανείς να υπολογίσει τη ζ(2n), για οποιοδήποτε θετικό ακέραιο n.
Άλλοι κοινοί συμβολισμοί[Επεξεργασία | επεξεργασία κώδικα]
Ο συμβολισμός cn είναι ανεπαρκής για να συζητηθούν οι συντελεστές Fourier διαφόρων συναρτήσεων. Ωστόσο, αντικαθίσταται συνήθως από μια τροποποιημένη μορφή της συνάρτησης (s, σ'αυτήν την περίπτωση), όπως ένα ή S, και ο συμβολισμός της συνάρτησης αντικαθίσταται συνήθως από τον παρακάτω τύπο.
Στη μηχανική, συγκεκριμένα όταν η μεταβλητή x εκφράζει χρόνο, ο συντελεστής της σειράς καλείται πεδίο συχνότητας αναπαράστασης. Οι αγκύλες χρησιμοποιούνται συχνά για να δώσουν έμφαση στο ότι το πεδίο αυτής της συνάρτησης είναι ένα διακριτό σύνολο συχνοτήτων.
Μια άλλη κοινή αναπαράσταση του πεδίου συχνοτήτων χρησιμοποιεί τους συντελεστές των σειρών Fourier για να διαμορφώσει τη χτένα Dirac:
όπου f αναπαριστά ένα συνεχές πεδίο συχνοτήτων. Όπου η μεταβλητή x έχει μονάδες δευτερολέπτων, f έχει μονάδες χέρτζ. Τα «δόντια» της χτένας Dirac έχουν τοποθετηθεί κατά πολλαπλάσια (π.χ. αρμονικές) του 1/P, το οποίο καλείται θεμελιώδης συχνότητα. Το μπορεί να αντικατασταθεί από την αναπαράσταση του αντίστροφου μετασχηματισμού Fourier:
Η συνάρτηση S(f) που δημιουργήσαμε συνήθως αναφέρεται ως μετασχηματισμός Fourier, μολονότι το ολοκλήρωμα Fourier της περιοδικής συνάρτησης δε συγκλίνει στις αρμονικές συχνότητες.[nb 2]
Ξεκίνημα[Επεξεργασία | επεξεργασία κώδικα]
| « |
πολλαπλασιάζοντας και τα 2 μέλη με , και τότε ολοκληρώνοντας από σε προκύπτει: |
» |
| — Joseph Fourier, Mémoire sur la propagation de la chaleur dans les corps solides. (1807)[9][nb 3] | ||
Αυτό δίνει άμεσα οποιοδήποτε συντελεστή ak της τριγωνομετρικής σειράς φ(y) για οποιαδήποτε συνάρτηση η οποία έχει τέτοια επέκταση. Λειτουργεί επειδή αν η φ έχει μια τέτοια επέκταση, τότε (κάτω από κατάλληλες προϋποθέσεις) το ολοκλήρωμα
μπορεί να εκτελέσει κάθε όρο χωριστά. Αλλά όλοι οι όροι περιέχουν για j ≠ k μηδενίζοντας τότε το ολοκλήρωμα από −1 εώς 1, αφήνοντας μόνο τον k οστό όρο.
Σε αυτές τις λίγες γραμμές, οι οποίες είναι κοντά στο σύγχρονο μαθηματικό φορμαλισμό χρησιμοποιούνται στις σειρές Fourier, ο Fourier δημιούργησε επανάσταση τόσο στα μαθηματικά όσο και στη φυσική. Αν και παρόμοιες τριγωνομετρικές συναρτήσεις έχουν χρησιμοποιηθεί προηγουμένως από τους Όιλερ, Ντ'Αλαμπέρ, Ντάνιελ Μπερνούλι και Γκάους, ο Φουριέ πίστευε ότι τέτοιες τριγωνομετρικές συναρτήσεις μπορούν να εκπροσωπήσουν οποιαδήποτε αυθαίρετη συνάρτηση. Η προσπάθεια για την εύρεση της πραγματικές αλήθειας οδήγησε σε σημαντικές θεωρίες, όπως της σύγκλισης, κενής συνάρτησης, και αρμονικής ανάλυσης. Όταν ο Fourier δημοσίευσε αργότερα ένα δοκίμιο σε έναν διαγωνισμό το 1811, η επιτροπή η οποία καταρτιζόταν από τους Lagrange, Λαπλάς, Μαλους και Λεζάντρ, μεταξύ πολλών) ανέφερε: ...ο τρόπος με τον οποίον ένας συγγραφέας φτάνει σε αυτές τις εξισώσεις αντιμετωπίζει πολλές δυσκολίες και...η ανάλυσή του για την απόδειξή τους αφήνει κάτι για βελτίωση στο σκορ της γενικότητας με μεγαλύτερη αυστηρότητα.
Γέννηση της αρμονικής ανάλυσης[Επεξεργασία | επεξεργασία κώδικα]
Από την εποχή του Fourier, πολλές διαφορετικές προσεγγίσεις για τον προσδιορισμό και την κατανόηση της έννοιας της σειράς Fourier έχουν αναπτυχθεί, οι οποίες συνάδουν η μία με την άλλη, αλλά η κάθε μία από τις οποίες τονίζουν διαφορετικές πτυχές του θέματος. Μερικές από τα πιο ισχυρές και κομψές προσεγγίσεις βασίζονται σε μαθηματικές ιδέες και εργαλεία που δεν ήταν διαθέσιμα κατά τα χρόνια του Fourier συμπληρώνοντας το πρωτότυπο έργο του. Ο Fourier όρισε αρχικά τη σειρά Fourier για πραγματικές συναρτήσεις, και χρησιμοποίησε αργότερα τις ημιτονοειδείς και συνημιτονοειδείς ως βασική οικογένεια αλγεβρικών συναρτήσεων για την αποσύνθεση.
Πολλοί άλλοι παρόμοιοι μετασχηματισμοί Fourier έκτοτε έχουν οριστεί, επεκτείνοντας την αρχική ιδέα σε άλλες εφαρμογές. Αυτός ο γενικός κλάδος της έρευνας ονομάζεται αρμονική ανάλυση. Μια σειρά Fourier, ωστόσο, μπορεί να χρησιμοποιηθεί μόνο για περιοδικές συναρτήσεις, ή για συναρτήσεις που οριοθετούνται σε (συμπαγές) διάστημα.
Επεκτάσεις[Επεξεργασία | επεξεργασία κώδικα]
Σειρές Φουριέ σε τετράγωνο[Επεξεργασία | επεξεργασία κώδικα]
Μπορούμε επίσης να ορίσουμε σειρές Φουριέ για συναρτήσεις με δύο μεταβλητές x και y στο τετράγωνο [−π, π]×[−π, π]:
Εκτός από το ότι είναι χρήσιμες για την επίλυση μερικών διαφορικών εξισώσεων όπως η εξίσωση της θερμότητας, μία αξιοσημείωτη εφαρμογή των σειρών Φουριέ σε τετράγωνο είναι η συμπίεση εικόνας. Ειδικότερα, η μορφή jpeg συμπίεσης εικόνων χρησιμοποιεί το δισδιάστατο διακριτό μετασχηματισμό συνημιτόνου, ο οποίος είναι ένας μετασχηματισμός Φουριέ που χρησιμοποιεί τις βασικές συνημιτονοειδείς συναρτήσεις.
Σειρές Φουριέ σε Bravais-πλέγμα-περιοδικών-συναρτήσεων[Επεξεργασία | επεξεργασία κώδικα]
Το πλέγμα Bravais ορίζεται ως το σύνολο των διανυσμάτων της μορφής:
όπου ni είναι ακέραιοι και ai είναι τρία γραμμικά ανεξάρτητα διανύσματα. Υποθέτοντας ότι έχουμε τυχαία συνάρτηση, f(r), η οποία ικανοποιεί την παρακάτω συνθήκη για οποιοδήποτε διάνυσμα πλέγματος Bravais R: f(r) = f(r + R), θα μπορούσαμε να φτιάξουμε μία σειρά Φουριέ. Αυτό το είδος συνάρτησης θα μπορούσε να είναι, για παράδειγμα, το ενεργό δυναμικό που ένα ηλεκτρόνιο "αισθάνεται" μέσα σε ένα περιοδικό κρύσταλλο. Είναι χρήσιμο να φτιάχνουμε μία σειρά Φουριέ του δυναμικού αφού έχουμε εφαρμόσει το θεώρημα του Bloch. Αρχικά, μπορούμε να γράψουμε οποιοδήποτε αυθαίρετο διάνυσμα r στο σύστημα συντεταγμένων του πλέγματος:
όπου ai = |ai|.
Έτσι μπορούμε να ορίσουμε μία νέα συνάρτηση,
Αυτή η νέα συνάρτηση, , είναι τώρα μία συνάρτηση τριών μεταβλητών, η κάθε μία από τις οποίες έχει περιοδικότητα a1, a2, a3 αντίστοιχα: . Αν γράψουμε μία σειρά του g στο διάστημα [0, a1] για x1, μπορούμε να ορίσουμε το εξής:
Και μετά μπορούμε να γράψουμε:
Ορίζοντας έτσι:
Μπορούμε να γράψουμε το g ακόμη μία φορά ως:
Τελικά εφαρμόζοντας το ίδιο για την τρίτη συντεταγμένη, ορίζουμε:
Γράφουμε το g ως:
Αναδιοργανώνουμε:
Τώρα, κάθε ανάστροφο πλέγμα διανυσμάτων μπορεί να γραφεί ως , όπου li είναι ακέραιοι και gi είναι το ανάστροφο πλέγμα διανυσμάτων, μπορούμε να χρησιμοποιήσουμε το γεγονός ότι για να υπολογίσουμε ότι για οποιοδήποτε αυθαίρετο ανάστροφο πλέγμα διανυσμάτων K και αυθαίρετο διάνυσμα στο χώρο r, το αριθμητικό τους γινόμενο είναι:
Είναι λοιπόν ξεκάθαρο ότι στη δική μας επέκταση, το άθροισμα εξαρτάται στην πραγματικότητα από το ανάστροφο πλέγμα διανυσμάτων:
όπου
Υποθέτοντας
μπορούμε να λύσουμε αυτό το σύστημα των τριών γραμμικών εξισώσεων ως προς x, y, και z συναρτήσει των x1, x2 και x3 προκειμένου να υπολογίσουμε το στοιχείο του όγκου σε ένα αρχέτυπο καρτεσιανό σύστημα συντεταγμένων. Από τη στιγμή που έχουμε τα x, y, και z συναρτήσει των x1, x2 και x3, μπορούμε να υπολογίσουμε την Ιακωβιανή ορίζουσα:
η οποία μετά από υπολογισμούς και εφαρμόζοντας μη τετριμμένες ταυτότητες εξωτερικού γινομένου μπορεί να αποδειχθεί ότι είναι ίση με:
(ίσως είναι επωφελές για χάρη της απλούστευσης των υπολογισμών, να δουλεύουμε σε ένα τέτοιο καρτεσιανό σύστημα συντεταγμένων, κατά το οποίο τυχαίνει το a1 να είναι παράλληλο στον άξονα των x, το a2 να ανήκει στο επίπεδο x-y, και το a3 έχει τις συνιστώσες του και στους τρεις άξονες). Ο παρονομαστής είναι ο όγκος της αρχικής μονάδας της στερεής σφαίρας ο οποίος περικλείεται από τα τρία αρχικά διανύσματα a1, a2 και a3. Πιο συγκεκριμένα, γνωρίζουμε πλέον ότι
Μπορούμε πλέον να γράψουμε το h(K) σαν ολοκλήρωμα με το παραδοσιακό σύστημα συντεταγμένων του όγκου της αρχικής στερεής σφαίρας, αντί με τις x1, x2 και x3 μεταβλητές:
Και το C είναι η αρχική μονάδα της στερεής σφαίρας, έτσι, είναι ο όγκος της αρχικής μονάδας της στερεής σφαίρας.
Ερμηνεία χώρου Hilbert[Επεξεργασία | επεξεργασία κώδικα]
Στη γλώσσα των χώρων Hilbert, το σύνολο των συναρτήσεων {; n ∈ Z} είναι μία ορθοκανονική βάση στο χώρο L2([−π, π]) των τετραγωνικά ολοκληρώσιμων συναρτήσεων στο [−π, π]. Αυτός ο χώρος είναι στην πραγματικότητα ένας χώρος Hilbert με εσωτερικό γινόμενο που δίνεται για δύο οποιαδήποτε στοιχεία f και g από τον τύπο
Οι βασικές σειρές Φουριέ που δίνουν αποτελέσματα για τους χώρους Hilbert μπορούν να γραφούν ως

Αυτό αντιστοιχεί ακριβώς στη μιγαδική εκθετική προσέγγιση που δίνεται παραπάνω. Η εκδοχή με τα ημίτονα και τα συνημίτονα αποδεικνύεται επίσης με την ερμηνεία του χώρου του Hilbert. Πράγματι,τα ημίτονα και τα συνημίτονα σχηματίζουν ένα ορθοκανονικό σύνολο:
(όπου δmn είναι το δέλτα του Κρόνεκερ), και
επιπλέον, τα ημίτονα και τα συνημίτονα είναι ορθογώνια στη συνεχή συνάρτηση 1. Μία ορθοκανονική βάση στον L2([−π, π]) αποτελείται από πραγματικές συναρτήσεις που σχηματίζονται από τις συναρτήσεις 1/√2π 1 και 1/√π cos(nx), 1/√π sin(nx) με n = 1, 2,... Η πυκνότητα του αναπτύγματός τους (span) είναι η συνέπεια του θεωρήματος Stone–Weierstrass, αλλά προκύπτει επίσης από τις ιδιότητες των κλασσικών πυρήνων όπως οι πυρήνες Fejér.
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Λέμε ότι η f ανήκει στο αν η f είναι 2π-περιοδική συνάρτηση στον R η οποία είναι k φορές διαφορίσιμη, και η k-οστή παράγωγος είναι συνεχής.
- Αν η f είναι μία 2π-περιοδική περιττή συνάρτηση, τότε an = 0 για κάθε n.
- Αν η f είναι μία 2π-περιοδική άρτια συνάρτηση, τότε bn = 0 για κάθε n.
- Αν η f είναι ολοκληρώσιμη, , και Το αποτέλεσμα αυτό είναι γνωστό ως λήμμα Riemann–Lebesgue.
- Μία διπλά απειροστή ακολουθία {an} στο c0(Z) είναι η ακολουθία των συντελεστών Φουριέ μίας συνάρτησης στον L1([0, 2π]) αν και μόνο αν είναι συνέλιξη δύο συναρτήσεων στον . Βλέπε [1]
- Αν , τότε οι συντελεστές Φουριέ της παραγώγου f′ μπορούν να εκφραστούν συναρτήσει των συντελεστών Φουριέ της συνάρτησης f, μέσω του τύπου .
- Αν , τότε . Πιο συγκεκριμένα, όταν η τείνει στο μηδέν, προκύπτει ότι το τείνει στο μηδέν, το οποίο σημαίνει ότι οι συντελεστές Φουριέ συγκλίνουν στο μηδέν πιο γρήγορα από την kοστή δύναμη του n.
- Το θεώρημα του Parseval. Αν η f ανήκει στον L2([−π, π]), τότε .
- Το Θεώρημα του Plancherel. Αν είναι συντελεστές και τότε υπάρχει μία μοναδική συνάρτηση τέτοια ώστε για κάθε n.
- Το πρώτο θεώρημα συνέλιξης υποστηρίζει ότι αν οι f και g ανήκουν στον L1([−π, π]), οι συντελεστές των σειρών Φουριέ της 2π-περιοδικής συνέλιξης των f και g δίνονται από τον τύπο:
- όπου:
- Το δεύτερο θεώρημα συνέλιξης υποστηρίζει ότι οι συντελεστές των σειρών Φουριέ του γινομένου των f και g δίνονται από τη διακριτή συνέλιξη των και ακολουθιών:
Συμπαγείς ομάδες[Επεξεργασία | επεξεργασία κώδικα]
Μία από τις ενδιαφέρουσες ιδιότητες των μετασχηματισμών Φουριέ που έχουμε αναφέρει, είναι ότι φέρουν συνέλιξη σε σημειακά γινόμενα. Αν αυτή είναι η ιδιότητα που ψάχνουμε να διατηρήσουμε, κάποιος μπορεί να παράγει σειρές Φουριέ σε οποιαδήποτε συμπαγή ομάδα. Τυπικά παραδείγματα περιλαμβάνουν τις κλασσικές ομάδες που είναι συμπαγείς. Αυτό γενικεύει τους μετασχηματισμούς Φουριέ σε όλους τους χώρους της μορφής L2(G), όπου G είναι ένας συμπαγής χώρος, με τέτοιο τρόπο ώστε οι μετασχηματισμοί Φουριέ να φέρουν συνελίξεις σε σημειακά γινόμενα. Οι σειρές Φουριέ υπάρχουν και συγκλίνουν με παρόμοιους τρόπους με αυτούς στο διάστημα [−π, π].
Μία εναλλακτική επέκταση των συμπαγών ομάδων είναι το θεώρημα Peter–Weyl, το οποίο αποδεικνύει τα αποτελέσματα των παρουσιάσεων των συμπαγών ομάδων ανάλογα με αυτά των πεπερασμένων ομάδων.
Πολλαπλότητα Riemann[Επεξεργασία | επεξεργασία κώδικα]

Αν το πεδίο ορισμού δεν είναι ομάδα, τότε δεν υπάρχει εγγενώς καθορισμένη συνέλιξη. Παρ' όλα αυτά, αν X είναι μία συμπαγής πολλαπλότητα Riemann, έχει τελεστή Laplace–Beltrami. Ο τελεστής Laplace–Beltrami είναι ένας διαφορικός τελεστής που αντιστοιχεί στον τελεστή Laplace για την πολλαπλότητα Riemann X. Έπειτα, αναλογικά, κάποιος μπορεί να σκεφτεί εξισώσεις θερμότητας στην X. Από τη στιγμή που ο Φουριέ έφθασε στη βάση του προσπαθώντας να λύσει την εξίσωση της θερμότητας, η φυσική γενίκευση είναι να χρησιμοποιήσουμε τις χαρακτηριστικές λύσεις των τελεστών Laplace–Beltrami σαν βάση. Αυτό γενικεύει τις σειρές Φουριέ σε χώρους της μορφής L2(X), όπου X είναι η πολλαπλότητα Riemann. Οι σειρές Φουριέ συγκλίνουν με παρόμοιους τρόπους με αυτούς στο διάστημα [−π, π]. Ένα τυπικό παράδειγμα είναι να πάρουμε την X ως σφαίρα με συνήθη μετρική, όπου η βάση Φουριέ αποτελείται από σφαιρικά αρμονικά.
Τοπικά συμπαγείς Αβελιανές ομάδες[Επεξεργασία | επεξεργασία κώδικα]
Η γενίκευση των συμπαγών ομάδων που συζητήθηκαν παραπάνω δεν γενικεύουν τις μη συμπαγείς, μη Αβελιανές ομάδες. Παρ' όλα αυτά υπάρχει μία απλή γενίκευση για τις Τοπικά Συμπαγείς Αβελιανές (ΤΣΑ) ομάδες.
Αυτό γενικεύει τους μετασχηματισμούς Φουριέ στους χώρους L1(G) ή L2(G), όπου G είναι μία ΤΣΑ ομάδα. Αν G είναι συμπαγής, λαμβάνεται επίσης μία σειρά Φουριέ, η οποία συγκλίνει παρόμοια με το διάστημα [−π, π], αλλά αν η G είναι μη συμπαγής, λαμβάνεται αντ' αυτού ένα ολοκλήρωμα Φουριέ. Αυτή η γενίκευση αποδίδει το συνήθη μετασχηματισμό Φουριέ όταν η υποκείμενη τοπικά συμπαγής Αβελιανή ομάδα είναι R.
Προσέγγιση και σύγκλιση των σειρών Φουριέ[Επεξεργασία | επεξεργασία κώδικα]
Μία σημαντική ερώτηση για τη θεωρία καθώς και τις εφαρμογές είναι αυτή της σύγκλισης.Πιο συγκεκριμένα, είναι συχνά απαραίτητο στις εφαρμογές να αντικαθιστούμε τις άπειρες σειρές από πεπερασμένες,
Αυτό καλείται μερικό άθροισμα. Θα θέλαμε να γνωρίζουμε, με ποια έννοια η fN(x) συγκλίνει στην f(x) με N → ∞.
Ιδιότητες ελαχίστων τετραγώνων[Επεξεργασία | επεξεργασία κώδικα]
Λέμε ότι το p είναι ένα τριγωνομετρικό πολυώνυμο βαθμού N όταν είναι της μορφής
Να σημειώσουμε ότι fN είναι τριγωνομετρικό πολυώνυμο βαθμού N. Από θεώρημα Parseval συνεπάγεται ότι
Θεώρημα. Το τριγωνομετρικό πολυώνυμο fN είναι το μοναδικό βέλτιστο τριγωνομετρικό πολυώνυμο βαθμού N που προσεγγίζει την f(x), υπό την έννοια ότι, για οποιοδήποτε τριγωνομετρικό πολυώνυμο p ≠ fN βαθμού N, έχουμε
όπου η νόρμα του χώρου Hilbert ορίζεται ως:
Σύγκλιση[Επεξεργασία | επεξεργασία κώδικα]
Λόγω της συμαντικότηταας της μεθόδου ελαχίστων τετραγώνων, και λόγω της πληρότητας των θεμέλιων της σειράς Fourier, έχουμε αποκτήσει ένα στοιχειώδες αποτέλεσμα σύγκλισης.
Θεώρημα. Αν f ανήκει στο L2([−π, π]), τότε f∞ συγκλίνει η f στο L2([−π, π]), το οποίο σημαίνει ότι, συγκλίνει στο 0 όταν N → ∞.
Έχουμε, ήδη, αναφέρει ότι, αν f διαφορίσιμη συνεχής συνάρτηση, τότε είναι ο nοστός συντελεστής της σειράς Fourier της παραγώγου f′. Επομένως, ουσιαστικά από την ανισότητα Κωσύ-Σβαρτς, όπου f∞ είναι απόλυτα αθροίσιμη. Το άθροισμα αυτής της σειράς είναι μία συνεχής συνάρτηση, ίση με f , δεδομένου ότι η σειρά Fourier συγκλίνει κατά μέση τιμή στην f:
Θεώρημα. Αν , τότε f∞ συγκλίνει στην f ομοιόμορφα (και επίσης, σημειακά.)
Το συμπέρασμα αυτό μπορεί να αποδειχτεί εύκολα, αν f επιπλέιο θεωρείται ότι είναι C2, μιας και σε αυτήν την περίπτωση τείνει στο μηδέν καθώς n → ∞. Γενικεύοντας, οι σειρές Fourier είναι απόλυτα αθρόισιμες, έτσι συγκλίνει ομοιόμορφα στην f, με την προϋπόθεση ότι η f ικανοποιεί τη συνθήκη Hölder προκειμένου α > ½. Στην περίπτωση της απόλυτης άθροισης, η ανισότητα αποδεικνύει την ομοιόμορφη σύγκλιση. Πολλά άλλα αποτελέσματα έχουν προκύψει για τη σύγκλιση των σειρών Fourier , κυμαίνονται από το απλό αποτέλεσμα ότι η σειρά συγκλίνει στο x αν η f είναι διαφορίσιμη στο x, τα αποτελέσματα του Lennart Carleson είναι πολύ πιο εξελιγμένα από ότι η σειρά Fourier μιας L2 συνάρτησης πραγματικής σύγκλισης σχεδόν παντού.
Αυτά τα θεωρήματα, και ανεπίσημες παραλλαγές τους που δεν διευκρινίζουν τις προϋποθέσεις σύγκλισης, αναφέρονται αρκετές φορές ως "θεώρημα του Fourier" ή "το θεώρημα Fourier".[10][11][12][13]
Απόκλιση[Επεξεργασία | επεξεργασία κώδικα]
Μιας και οι σειρές Fourier έχουν τόσο καλές ιδιότητες σύγκλισης, πολλοί εκπλήσσονται συχνά όταν προκύπτουν αρνητικά αποτελέσματα. Για παράδειγμα, η σειρά Fourier μιας συνεχούς περιοδικής συνάρτησης Τ δεν χρειάζεται να συγκλίνει κατά σημείο. Η αρχή ομοιόμορφου φράγματος αποδίδει μία απλή μη εποικοδομητική απόδειξη αυτού του γεγονότος.
Το 1922, ο Αντρέι Κολμογκόροφ δημοσίευσε ένα άρθρο με τίτλο "Une série de Fourier-Lebesgue divergente presque partout" στο οποίο έδωσε ένα παράδειγμα μιας ολοκληρώσιμης-Lebesgue συνάρτησης, της οποίας η σειρά Fourier αποκλίνει σχεδόν παντού. Αργότερα, επίσης, κατασκεύασε μία ολοκληρώσιμη συνάρτηση όπου η σειρά Fourier της αποκλίνει παντού (Katznelson 1976).
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- ATS θεώρημα
- Πυρήνας Dirichlet
- Διακριτός μετασχηματισμός Fourier
- Μετασχηματισμός Fast Fourier
- Σειρές Fourier ημιτόνου και συνημιτόνου
- Θεώρημα του Fejér
- Φαινόμενο Γκιμπς
- Σειρά Laurent-η αντικατάσταση q = eix μετασχηματίζει μια σειρά Fourier σε σειρά Laurent, ή αντίστροφα. Αυτό χρησιμοποιείται στην q-σειρά επέκταση της j-αναλλοίωτης.
- Πολυδιάστατος μετασχηματισμός
- Φασματική θεωρία
- Θεώρημα Sturm-Liouville
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Αυτοί οι τρεις έκαναν κάποιου είδους σημαντική δουλειά πάνω στην κυματική εξίσωση, ειδικά ο D'Alembert. Η δουλειά του Euler σε αυτόν τον τομέα ήταν κυρίως σύγχρονη/ σε συνεργασία με τον Bernoulli, αν και ο Bernoulli έκανε κάποιες ανεξάρτητες συνεισφορές στη θεωρία των κυμάτων και των ταλαντώσεων (βλέπε, pg.s 209 & 210, ).
- ↑ Αφού το ολοκλήρωμα που ορίζει ο μετασχηματισμός Fourier της περιοδικής συνάρτησης δε συγκλίνει, είναι απαραίτητο να εξετάσουμε την περιοδική συνάρτηση και τη μετατροπή της ως κατανομή. Με αυτήν την έννοια είναι μία δέλτα συνάρτηση Dirac, η οποία είναι γνωστό παράδειγμα κατανομών.
- ↑ Αυτά τα λόγια δεν είναι αυστηρά του Φουριέ. Ενώ στο άρθρο παρατίθενται ο Φουριέ ως συγγραφέας του, επισημαίνεται σε σχετική υποσημείωση ότι το άρθρο έχει γραφτεί στην πραγματικότητα από τον Poisson (το γεγονός ότι δεν έχει γραφτεί από το Φουριέ είναι επίσης ξεκάθαρο από τη συνεπή χρήση του τρίτου προσώπου για να αναφερθεί σ' αυτόν) και ότι παρουσιάζεται, "για λόγους ιστορικού ενδιαφέροντος", σαν να ήταν του Φουριέ πραγματική memoire.
- ↑ Ο παράγοντας της κλίμακας είναι πάντα ίσος με την περίοδο, 2π σε αυτήν την περίπτωση.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Lejeune-Dirichlet, P. "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données". (In French), transl. "On the convergence of trigonometric series which serve to represent an arbitrary function between two given limits". Journal f¨ur die reine und angewandte Mathematik, Vol. 4 (1829) pp. 157–169.
- ↑ «Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe» [About the representability of a function by a trigonometric series]. Habilitationschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind (στα Γερμανικά). Αρχειοθετήθηκε από το πρωτότυπο στις 20 Μαΐου 2008. Ανακτήθηκε στις 19 Μαΐου 2008.
- ↑ D. Mascre, Bernhard Riemann: Posthumous Thesis on the Representation of Functions by Triginometric Series (1867). Landmark Writings in Western Mathematics 1640–1940, Ivor Grattan-Guinness (ed.); pg. 492. Elsevier, 20 May 2005.Accessed 7 Dec 2012.</
- ↑ Theory of Complex Functions: Readings in Mathematics, by Reinhold Remmert; pg 29. Springer, 1991. Accessed 7 Dec 2012.
- ↑ Nerlove, Marc· Grether, David M.· Carvalho, Jose L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics
 . Elsevier. ISBN 0-12-515751-7.
. Elsevier. ISBN 0-12-515751-7.
- ↑ Flugge, Wilhelm (1957). Statik und Dynamik der Schalen. Berlin: Springer-Verlag.
- ↑ Dorf, Richard C.· Tallarida, Ronald J. (15 Ιουλίου 1993). Pocket Book of Electrical Engineering Formulas (1η έκδοση). Boca Raton,FL: CRC Press. σελίδες 171–174. ISBN 0849344735.
- ↑ Georgi P. Tolstov (1976). Fourier Series. Courier-Dover. ISBN 0-486-63317-9.
- ↑ Gallica – Fourier, Jean-Baptiste-Joseph (1768–1830). Oeuvres de Fourier. 1888, pp. 218–219,
- ↑ William McC. Siebert (1985). Circuits, signals, and systems. MIT Press. σελ. 402. ISBN 978-0-262-19229-3.
- ↑ L. Marton· Claire Marton (1990). Advances in Electronics and Electron Physics. Academic Press. σελ. 369. ISBN 978-0-12-014650-5.
- ↑ Hans Kuzmany (1998). Solid-state spectroscopy. Springer. σελ. 14. ISBN 978-3-540-63913-8.
- ↑ Karl H. Pribram· Kunio Yasue· Mari Jibu (1991). Brain and perception. Lawrence Erlbaum Associates. σελ. 26. ISBN 978-0-89859-995-4.[νεκρός σύνδεσμος]
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- William E. Boyce· Richard C. DiPrima (2005). Elementary Differential Equations and Boundary Value Problems (8η έκδοση). New Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier (2003) [1822]. Théorie Analytique de la Chaleur [The Analytical Theory of Heat)]. Μτφρ. Alexander Freeman. Dover Publications. ISBN 0-486-49531-0. [Αρχική έκδοση 1822 στα Γαλλικά. Η έκδοση του 2003 αποτελεί επανέκδοση της μετάφρασης του 1878 από τον Alexander Freeman.]
- Enrique A. Gonzalez-Velasco (1992). «Connections in Mathematical Analysis: The Case of Fourier Series». American Mathematical Monthly 99 (5): 427–441. doi:. https://archive.org/details/sim_american-mathematical-monthly_1992-05_99_5/page/427.
- Katznelson, Yitzhak (1976). An introduction to harmonic analysis (Διορθωμένη 2η έκδοση). New York: Dover Publications, Inc. ISBN 0-486-63331-4.
- Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin (1976). Principles of mathematical analysis (3η έκδοση). New York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002) [1935]. Trigonometric series (3η έκδοση). Cambridge: Cambridge University Press. ISBN 0-521-89053-5.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- thefouriertransform.com Fourier Series as a prelude to the Fourier Transform
- [2]-Characterizations of a linear subspace associated with Fourier series
- An interactive flash tutorial for the Fourier Series
- Phasor Phactory Allows custom control of the harmonic amplitudes for arbitrary terms
- Java applet shows Fourier series expansion of an arbitrary function
- Example problems Αρχειοθετήθηκε 2008-04-10 στο Wayback Machine. – Examples of computing Fourier Series
- Hazewinkel, Michiel, επιμ.. (2001), «Fourier series», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/f041090
- Weisstein, Eric W., "Fourier Series" από το MathWorld.
- Fourier Series Module by John H. Mathews
- Joseph Fourier – A site on Fourier's life which was used for the historical section of this article
- SFU.ca – 'Fourier Theorem'
|


![{\displaystyle \scriptstyle [x_{0},\ x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15dd8a7d5176a8625325e2afb151fbdd825a142)














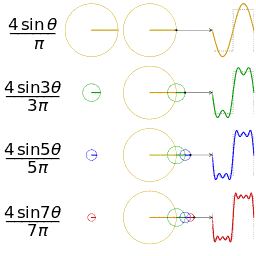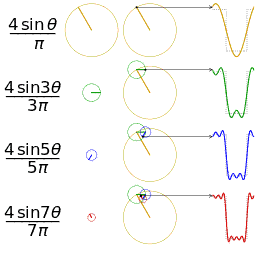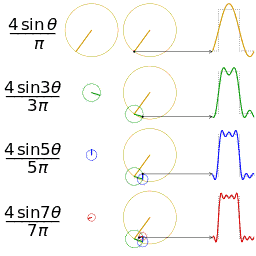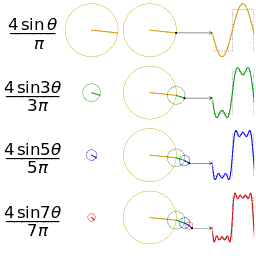




![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbf {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f7723030e9a65dde2b59bdffde660c5ac6d1a4)


![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i{\tfrac {2\pi nx}{P}}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j{\tfrac {2\pi nx}{P}}}&&\scriptstyle {\text{common engineering notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1948743e8e50b99560a2e018c78b35e14e2111a1)
![{\displaystyle S(f)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/191fd9d4420479ce5300b692fbc43c0e5e703e89)

![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i{\tfrac {2\pi nx}{P}}}\ \ {\stackrel {\mathrm {def} }{=}}\ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f87bc7f858006ce49e2b5c40d429076b92b96df)
















![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&:={\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&:={\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)








![{\displaystyle {\begin{bmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[3pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[3pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5095a317a5c0975c5d1bdf27cd79d13b106a96a6)


























![{\displaystyle f\in L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)

=2\pi \cdot {\hat {f}}(n)\cdot {\hat {g}}(n),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
\ &{\stackrel {\mathrm {def} }{=}}\int _{-\pi }^{\pi }f(u)\cdot g[{\text{pv}}(x-u)]du,&&{\big (}{\text{and }}\underbrace {{\text{pv}}(x)\ {\stackrel {\mathrm {def} }{=}}{\text{Arg}}\left(e^{ix}\right)} _{\text{principal value}}{\big )}\\&=\int _{-\pi }^{\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when g(x) is 2}}\pi {\text{-periodic.}}\\&=\int _{2\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when both functions are 2}}\pi {\text{-periodic, and the integral is over any 2}}\pi {\text{ interval.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1223be49e9c8285ec78e1a81ac52e7f983702eeb)


=[{\hat {f}}*{\hat {g}}](n).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)










