Πολικό σύστημα συντεταγμένων
| Το λήμμα παραθέτει τις πηγές του αόριστα, χωρίς παραπομπές. |
Στα μαθηματικά, το πολικό σύστημα συντεταγμένων είναι ένα δισδιάστατο σύστημα συντεταγμένων στο οποίο η θέση οποιουδήποτε σημείου σε ένα επίπεδο καθορίζεται από την απόσταση του σημείου αυτού από ένα αυθαίρετα επιλεγμένο σημείο αναφοράς και τη γωνία από μία αυθαίρετα επιλεγμένη κατεύθυνση.
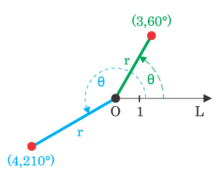
Η απόσταση ενός σημείου από το αυθαίρετα επιλεγμένο σημείο αναφοράς (για το οποίο είθισται να επιλέγεται η αρχή των αξόνων) ονομάζεται ακτινική συντεταγμένη ή απλώς ακτίνα και συμβολίζεται συνήθως με το λατινικό r (από την αγγλική λέξη radius, «ακτίνα»), ενώ η γωνία που σχηματίζει η ακτίνα του σημείου με μία αυθαίρετα επιλεγμένη διεύθυνση (συνήθως ένας από τους δύο κύριους άξονες συντεταγμένων) ονομάζεται γωνιακή συντεταγμένη ή αζιμούθιο και συμβολίζεται συνήθως με το ελληνικό πεζό γράμμα θ.
Ιστορικό[Επεξεργασία | επεξεργασία κώδικα]
Δείτε επίσης: Ιστορικό τριγωνομετρικών συναρτήσεων Οι έννοιες της γωνίας και ακτίνας είχαν ήδη χρησιμοποιηθεί από τους αρχαίους λαούς της 1ης χιλιετίας π.Χ..Ο Έλληνας αστρονόμος και αστρολόγος Ίππαρχος (190-120 π.Χ.), δημιούργησε έναν πίνακα συναρτήσεων με χορδές δίνοντας το μήκος της χορδής για κάθε γωνία, και υπάρχουν αναφορές για τη χρήση πολικών συντεταγμένων για την εύρεση αστρικών θέσεων. Στις Σπείρες, ο Αρχιμήδης περιγράφει την σπείρα του Αρχιμήδη, μια συνάρτηση στην οποία η ακτίνα εξαρτάται από τη γωνία.Το ελληνικό έργο, ωστόσο, δεν επεκτείνεται σε ένα πλήρες σύστημα συντεταγμένων.
Από τον 8ο αιώνα μ.Χ. και μετά, οι αστρονόμοι ανέπτυξαν μεθόδους προσέγγισης και υπολογισμού της κατεύθυνσης στη Μέκκα (qibla) - και την απόσταση της- από οποιαδήποτε τοποθεσία πάνω στη Γη.Από τον 9ο αιώνα και μετά χρησιμοποιούσαν τη σφαιρική τριγωνομετρία και τη χαρτογραφική προβολή για να υπολογίσουν αυτές τις ποσότητες με ακρίβεια. Ο υπολογισμός είναι ουσιαστικά η μετατροπή των γεωγραφικών συντεταγμένων της Μέκκας (δηλαδή το γεωγραφικό μήκος και πλάτος) σε πολικές συντεταγμένες (δηλαδή την κατεύθυνση και την απόσταση) σε σχέση με ένα σύστημα αναφοράς του οποίου ο μεσημβρινός είναι ένας μεγάλος κύκλος ανάμεσα στην δεδομένη θέση και τους πόλους της Γης , και ο πολικός άξονας είναι η γραμμή που διέρχεται από την τοποθεσία και το αντιδιαμετρικό της σημείο.
Υπάρχουν διάφορες πηγές με θέμα την εισαγωγή των πολικών συντεταγμένων ως μέρος ενός επίσημου συστήματος συντεταγμένων. Η πλήρης ιστορία του θέματος περιγράφεται στο βιβλίο του καθηγητή του πανεπιστημίου του Χάρβαρντ Julian Lowell Coolidge Origin of Polar Coordinates.Οι Grégoire de Saint-Vincent και Μποναβεντούρα Καβαλιέρι εισήγαγαν ανεξάρτητα τις συγκεκριμένες έννοιες στα μέσα του δέκατου έβδομου αιώνα.Ο Saint-Vincent έγραψε για τις πολικές συντεταγμένες το 1625 και δημοσίευσε το έργο του το 1647, ενώ ο Καβαλιέρι δημοσίευσε το δικό του έργο το 1635 με μια διορθωμένη έκδοση του να εμφανίζεται το 1653.Ο Καβαλιέρι χρησιμοποίησε για πρώτη φορά πολικές συντεταγμένες για να λύσει το πρόβλημα που σχετίζεται με την περιοχή ανάμεσα στην σπείρα του Αρχιμήδη.Ο Blaise Pascal ακολούθως χρησιμοποίησε πολικές συντεταγμένες για να υπολογίσετε το μήκος των παραβολικών τόξων.
Στο Method of Fluxions (γράφτηκε το 1671, δημοσιεύθηκε το 1736),ο Isaac Newton εξέτασε τη μετατροπή σε πολικές συντεταγμένες,στις οποίες αναφέρεται ως "Έβδομος τρόπος: Για Σπείρες», και εννέα άλλα συστήματα συντεταγμένων. Στο περιοδικό Acta Eruditorum (1691), ο Jacob Bernoulli χρησιμοποίησε ένα σύστημα με μια τελεία πάνω σε μια γραμμή, που ονομάζεται πόλος και πολικός άξονας αντίστοιχα. Οι συντεταγμένες προσδιορίζονται από την απόσταση από τον πόλο και τη γωνία από τον πολικό άξονα. Το έργο του Bernoulli επεκτάθηκε για την εύρεση της ακτίνας καμπυλότητας των καμπυλών σε πολικές συντεταγμένες.
Ο πραγματικός όρος πολικές συντεταγμένες κατανέμεται στον Gregorio Fontana και χρησιμοποιήθηκε από Ιταλούς συγγραφείς του 18ου αιώνα. Ο όρος εμφανίστηκε στα αγγλικά το 1816 στη μετάφραση του George Peacock του έργου του Lacroix Differential and Integral Calculus.Ο Alexis Clairaut ήταν ο πρώτος που σκέφτηκε πολικές συντεταγμένες σε τρεις διαστάσεις, και ο Leonhard Euler ήταν ο πρώτος που τις ανέπτυξε στην πραγματικότητα.
Μαθηματική περιγραφή[Επεξεργασία | επεξεργασία κώδικα]

Όπως ακριβώς στο καρτεσιανό σύστημα συντεταγμένων κάθε σημείο με συντεταγμένες (x0,y0) αντιστοιχεί στην τομή των ευθειών x=x0 και y=y0, έτσι και στο πολικό σύστημα συντεταγμένων κάθε σημείο καθορίζεται μονοσήμαντα από την τομή ενός κύκλου σταθερής ακτίνας r=r0 και μίας ευθείας που καθορίζεται από μία σταθερή τιμή γωνίας θ=θ0.
Οι καμπύλες σταθερής ακτίνας r και γωνίας θ ορίζουν το λεγόμενο «πολικό πλέγμα», το οποίο θυμίζει ιστό αράχνης.
Συνήθεις συμβάσεις[Επεξεργασία | επεξεργασία κώδικα]
Οι συνηθισμένες συμβάσεις όσον αφορά την επιλογή του σταθερού σημείου αναφοράς και της σταθερής κατεύθυνσης από την οποία μετράται το αζιμούθιο είναι:
- Η ακτινική συντεταγμένη ενός σημείου αναφέρεται ως προς την αρχή των αξόνων (0,0)
- Το αζιμούθιο μετράται από τον θετικό οριζόντιο άξονα με φορά αντίθετη από εκείνη των δεικτών του ρολογιού
Το αζιμούθιο μετράται συνήθως σε ακτίνια αντί για μοίρες.
Σχέση με τις καρτεσιανές συντεταγμένες[Επεξεργασία | επεξεργασία κώδικα]

Η σχέση μεταξύ πολικών (r,θ) και καρτεσιανών (x,y) συντεταγμένων στο επίπεδο δίνεται από τις παρακάτω σχέσεις μετατροπής:
Διανυσματικός λογισμός[Επεξεργασία | επεξεργασία κώδικα]
Τα διανύσματα θέσης και στις πολικές συντεταγμένες σχετίζονται με τα αντίστοιχα μοναδιαία διανύσματα και των καρτεσιανών σύμφωνα με τις παρακάτω γενικές εξισώσεις μετατροπής συντεταγμένων:
όπου
Η εφαρμογή των παραπάνω τύπων μας δίνουν τα παρακάτω αποτελέσματα:
Είναι φανερό ότι τα διανύσματα και είναι ορθομοναδιαία (δηλαδή έχουν μέτρο μονάδα και είναι κάθετα μεταξύ τους). Επιπροσθέτως, τα διανύσματα αυτά δεν είναι σταθερά, δηλαδή η φορά τους μεταβάλλεται από σημείο σε σημείο σε αντίθεση με τα μοναδιαία διανύσματα και των καρτεσιανών συντεταγμένων τα οποία είναι σταθερά παντού στο επίπεδο. Μία άμεση μαθηματική συνέπεια του γεγονότος αυτού είναι ότι
Τελεστής ανάδελτα[Επεξεργασία | επεξεργασία κώδικα]
Σε δισδιάστατες καρτεσιανές συντεταγμένες, ο τελεστής ανάδελτα δίνεται από τον τύπο:
Με αφετηρία τις εξισώσεις μετατροπής από καρτεσιανές σε πολικές συντεταγμένες, αποδεικνύεται ότι ο παραπάνω τελεστής δίνεται σε πολικές συντεταγμένες από τον εξής τύπο:
Λαπλασιανή[Επεξεργασία | επεξεργασία κώδικα]
Έχοντας ορίσει την μορφή του τελεστή ανάδελτα σε πολικές συντεταγμένες, μπορούμε να βρούμε τη μορφή του Λαπλασιανού τελεστή στο ίδιο σύστημα συντεταγμένων:
Τροχιές σωμάτων σε πολικές συντεταγμένες[Επεξεργασία | επεξεργασία κώδικα]
Στη Φυσική, η τροχιά ενός σώματος ως προς ένα επιλεγμένο σύστημα συντεταγμένων μπορεί να περιγραφτεί μαθηματικά από ένα διάνυσμα r που ονομάζεται ακτίνα θέσης ή επιβατική ακτίνα του σώματος. Η ακτίνα θέσης, η ταχύτητα v και η επιτάχυνση a περιγράφονται από τα διανύσματα:
όπου η τελεία αναφέρεται σε παραγώγιση ως προς το χρόνο. Οι ακριβείς σχέσεις για την ταχύτητα και την επιτάχυνση αποδεικνύονται εύκολα παραγωγίζοντας την ακτίνα θέσης ως προς το χρόνο.
Απειροστικός λογισμός[Επεξεργασία | επεξεργασία κώδικα]
Στον απειροστικό λογισμό η αναπαράσταση μαθηματικών συναρτήσεων σε πολικές συντεταγμένες είναι πολλές φορές χρησιμότερη σε σχέση με τις καρτεσιανές συντεταγμένες. Παρακάτω παρατίθενται μερικές από τις εφαρμογές των πολικών συντεταγμένων σε προβλήματα διαφορικού και ολοκληρωτικού λογισμού.
Μήκος καμπύλης[Επεξεργασία | επεξεργασία κώδικα]
Εν γένει, το μήκος μίας καμπύλης μπορεί να υπολογισθεί μέσω ενός ολοκληρώματος αν παραμετρήσουμε τη καμπύλη αυτή με μία αυθαίρετη παράμετρο λ. Συγκεκριμένα, αν υποθέσουμε ότι οι συντεταγμένες (σε δύο διαστάσεις) κάθε σημείου μίας καμπύλης είναι συναρτήσεις της παραμέτρου λ και ότι κάθε σημείο αντιστοιχεί σε μία συγκεκριμένη τιμή της παραμέτρου, τότε το μήκος μεταξύ δύο σημείων Α και Β της καμπύλης θα ισούται με
όπου υποθέσαμε ότι οι τιμές της παραμέτρου λ στα σημεία Α και Β είναι a και b αντίστοιχα. Επίσης, ds είναι το στοιχειώδες μήκος της καμπύλης. Η παραπάνω σχέση ισχύει αν ο χώρος είναι Ευκλείδειος, στην οποία περίπτωση σύμφωνα με το Πυθαγόρειο Θεώρημα:
Σε πολικές συντεταγμένες το στοιχειώδες μήκος καμπύλης ισούται με
Συνεπώς, αφού κάθε καμπύλη περιγράφεται από τη συνάρτηση r(θ) που μας δίνει την απόσταση r κάθε σημείου της καμπύλης από την αρχή των αξόνων για δεδομένη τιμή της γωνίας θ, μπορούμε να χρησιμοποιήσουμε ως παράμετρο στο ολοκλήρωμα που μας δίνει το μήκος μεταξύ δύο σημείων της καμπύλης Α και Β τη γωνία θ. Άρα λοιπόν,
| Εφαρμογή του παραπάνω τύπου για τον υπολογισμό της περιμέτρου ενός κύκλου. |
|---|
|
Έστω κύκλος ακτίνας R, με κέντρο την αρχή των αξόνων. Κάθε σημείο του κύκλου μπορεί να περιγραφτεί από τη συνάρτηση η οποία μας πληροφορεί ότι κάθε σημείο του κύκλου απέχει απόσταση R από το κέντρο του. Για να υπολογίσουμε τη περίμετρο C, αρκεί να κάνουμε χρήση του προηγούμενου ολοκληρώματος με όρια ολοκλήρωσης από θ=0 μέχρι θ=2π. Συνεπώς, Που είναι ο γνωστός τύπος της περιμέτρου ενός κύκλου ακτίνας R. |
Εμβαδόν[Επεξεργασία | επεξεργασία κώδικα]

Έστω μία καμπύλη που περιγράφεται από τη συνάρτηση r(θ). Το εμβαδόν του χωρίου R που ορίζουν η καμπύλη r(θ) και οι ευθείες θ=a, θ=b μπορεί να υπολογισθεί σε πολικές συντεταγμένες αν τμήσουμε το εν λόγω χωρίο σε έναν άπειρο αριθμό στοιχειωδών τριγώνων εμβαδού
Η παραπάνω έκφραση προκύπτει από τον βασικό τύπο που μας δίνει το εμβαδόν ενός τριγώνου (βάση×ύψος/2), αν αναλογισθούμε ότι η βάση του απειροστού τριγώνου ισούται με το μήκος τόξου που διαγράφει η επιβατική ακτίνα r(θ) κατά μία απειροστή γωνιακή μετατόπιση από θ σε θ+dθ, το οποίο ισούται με ds=rdθ. Το ύψος αντίστοιχα, αφού κατά την απειροστή γωνιακή μετατόπιση το μέτρο της επιβατική ακτίνας πρακτικά δεν έχει αλλάξει, θα ισούται με r.
Αν Α λοιπόν το συνολικό εμβαδόν που περικλείει το χωρίο R, τότε
| Εφαρμογή του παραπάνω τύπου για τον υπολογισμό του εμβαδού ενός κύκλου. |
|---|
|
Έστω κύκλος ακτίνας R, με κέντρο την αρχή των αξόνων. Κάθε σημείο του κύκλου μπορεί να περιγραφτεί από τη συνάρτηση η οποία μας πληροφορεί ότι κάθε σημείο του κύκλου απέχει απόσταση R από το κέντρο του. Για να υπολογίσουμε το εμβαδόν Α, αρκεί να κάνουμε χρήση του προηγούμενου ολοκληρώματος με όρια ολοκλήρωσης από θ=0 μέχρι θ=2π. Συνεπώς, Που είναι ο γνωστός τύπος του εμβαδού ενός κύκλου ακτίνας R. |
Μετρική στον Ευκλείδειο χώρο[Επεξεργασία | επεξεργασία κώδικα]
Στη διαφορική γεωμετρία, η μετρική του δισδιάστατου Ευκλείδειου χώρου μπορεί να γραφτεί σε πολικές συντεταγμένες υπό μορφή ενός 2×2 πίνακα με τον ακόλουθο τρόπο:
Σύμφωνα με τον παραπάνω ορισμό, και υιοθετώντας την σύμβαση άθροισης του Αϊνστάιν, μπορούμε να γράψουμε το τετράγωνο του στοιχείου μήκους στον δισδιάστατο Ευκλείδειο χώρο ως εξής:
όπου θεωρήσαμε ότι οι δείκτες άθροισης μ,ν παίρνουν τις τιμές 1,2 και
Εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]
Οι πολικές συντεταγμένες είναι δύο διαστάσεων και επομένως μπορούν να χρησιμοποιηθούν μόνον όταν τα σημεία θέσης βρίσκονται σε ένα ενιαίο δισδιάστατο επίπεδο.Είναι πιο κατάλληλες σε κάθε πλαίσιο, όπου το φαινόμενο που εξετάζεται είναι εγγενώς συνδεδεμένο με την κατεύθυνση και το μήκος από ένα κεντρικό σημείο.Για παράδειγμα, τα παραπάνω παραδείγματα δείχνουν πως οι στοιχειώδεις πολικές εξισώσεις αρκούν για να καθορίσουν τις καμπύλες-όπως η σπείρα του Αρχιμήδη-των οποίων η εξίσωση στο καρτεσιανό σύστημα συντεταγμένων θα είναι πολύ πιο περίπλοκη.Επιπλέον, πολλά φυσικά συστήματα -όπως εκείνα που συνδέονται με φορείς που κινούνται γύρω από ένα κεντρικό σημείο ή με φαινόμενα που δημιουργούνται από ένα κεντρικό σημείο- είναι απλούστερα και πιο κατανοητά στη μοντελοποίηση χρησιμοποιώντας πολικές συντεταγμένες.Το αρχικό κίνητρο για την εισαγωγή των πολικών συστημάτων ήταν η μελέτη της κυκλικής και της τροχιακής κίνησης.
Θέση και πλοήγηση[Επεξεργασία | επεξεργασία κώδικα]
Οι πολικές συντεταγμένες χρησιμοποιούνται συχνά στην πλοήγηση, όπως μπορεί να δοθεί ο προορισμός ή κατεύθυνση κίνησης, όπως η γωνία και η απόσταση από το αντικείμενο που εξετάζεται.Για παράδειγμα, τα αεροσκάφη χρησιμοποιούν μια ελαφρώς τροποποιημένη εκδοχή των πολικών συντεταγμένων για την πλοήγηση.Σε αυτό το σύστημα, το ένα που χρησιμοποιείται γενικά για οποιοδήποτε είδος πλοήγησης, το 0 ° ακτίνων γενικά ονομάζεται κλάση 360, και οι γωνίες να συνεχίσουν σε μια δεξιόστροφη κατεύθυνση, αντί αριστερόστροφα, όπως στο μαθηματικό σύστημα.Η κλάση 360 αντιστοιχεί σε μαγνητικό βορρά, ενώ οι κλάσεις 90, 180, και 270 αντιστοιχούν σε μαγνητική ανατολή, νότο και δύση, αντίστοιχα.Έτσι, ένα αεροσκάφος που ταξιδεύει 5 ναυτικά μίλια ανατολικά θα ταξιδέψει 5 μονάδες στην κλάση 90 (διαβάστε επίσης zero-niner-zero από τον έλεγχο εναέριας κυκλοφορίας).
Μοντελοποίηση[Επεξεργασία | επεξεργασία κώδικα]
Συστήματα που εμφανίζουν ακτινωτή συμμετρία παρέχουν φυσικές ρυθμίσεις για το πολικό σύστημα συντεταγμένων, με το κεντρικό σημείο να ενεργεί ως πόλος.Ένα χαρακτηριστικό παράδειγμα αυτής της χρήσης είναι η εξίσωση ροής των υπόγειων υδάτων, όταν εφαρμόζεται σε ακτινικά συμμετρικά πηγάδια.Συστήματα με ακτινική ισχύ είναι επίσης καλοί υποψήφιοι για τη χρήση του συστήματος πολικής συντεταγμένης. Τα συστήματα αυτά περιλαμβάνουν βαρυτικά πεδία, τα οποία υπακούουν στο νόμο του αντιστρόφου τετραγώνου, καθώς και σε συστήματα με σημειακές πηγές, όπως ραδιοφωνικές κεραίες.Ακτινικά συμμετρικά συστήματα μπορούν επίσης να είναι μοντελοποιημένα με πολικές συντεταγμένες. Για παράδειγμα, ένα μικρόφωνο Pickup έχει ανάλογη ανταπόκριση σε ένα εισερχόμενο ήχο από μία δεδομένη κατεύθυνση, και αυτά τα μοτίβα μπορούν να παρασταθούν ως πολικές καμπύλες.Η καμπύλη για ένα πρότυπο καρδιοειδές μικρόφωνο, το πιο κοινό μικρόφωνο μίας κατεύθυνσης, μπορεί να παρασταθεί ως r = 0,5 + 0.5ημ (φ) σε κάθε συχνότητα του σχεδιασμού του στόχου της. Το σχέδιο μετατοπίζεται και σε χαμηλότερες συχνότητες.
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- Finney, R.L., Giordano F.R. (2005). Απειροστικός λογισμός, Τόμος Ι. Ελληνική μετάφραση. Πανεπιστημιακές Εκδόσεις Κρήτης.
- Finney, R.L., Giordano F.R. (2005). Απειροστικός λογισμός, Τόμος ΙΙ. Ελληνική μετάφραση. Πανεπιστημιακές Εκδόσεις Κρήτης.



















![{\displaystyle L_{AB}=\int _{A}^{B}{\sqrt {\left({\frac {dr(\theta )}{d\theta }}\right)^{2}+[r(\theta )]^{2}}}\ d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f3add1cd96dd1aa433778cde22d125b2c4afcda2)







