Οκτάεδρο
| Το λήμμα παραθέτει τις πηγές του αόριστα, χωρίς παραπομπές. |
| Οκτάεδρο | |
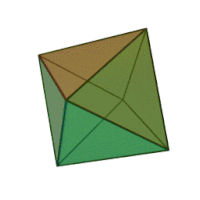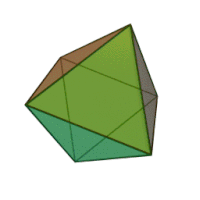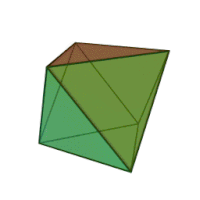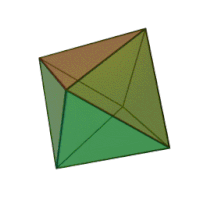
| |
| Τύπος | Πλατωνικό στερεό |
| Έδρες | 8 τρίγωνα |
| Ακμές | 12 |
| Κορυφές | 6 |
| Διαμόρφωση κορυφής |  (3.3.3.3) |
| Σύμβολο Σλέφλι (Schläfli) | {3,4} |
| Ομάδα συμμετρίας | οκταεδρική (Oh) |
| Δυϊκό | Κύβος |
| Ανάπτυγμα | 
|
Στη στερεομετρία, οκτάεδρο λέγεται ένα πολύεδρο που έχει οκτώ έδρες.
Το κανονικό οκτάεδρο είναι ένα από τα Πλατωνικά στερεά, που έχει για έδρες οκτώ ισόπλευρα τρίγωνα, τα οποία ενώνονται ανά τέσσερα σε κάθε κορυφή του.
Άλλα οκτάεδρα είναι το κόλουρο τετράεδρο, το εξαγωνικό πρίσμα, η επταγωνική πυραμίδα κ.ά.
Γεωμετρικά χαρακτηριστικά κανονικού οκταέδρου[Επεξεργασία | επεξεργασία κώδικα]
Αν θεωρήσουμε το μήκος της ακμής του οκταέδρου, τότε ισχύουν τα εξής:
| Ακτίνα περιγεγραμμένης σφαίρας (απόσταση κορυφών από το κέντρο) |
|
| Ακτίνα εγγεγραμμένης σφαίρας (απόσταση εδρών από το κέντρο) |
|
| Απόσταση ακμών από το κέντρο | |
| Συνολική επιφάνεια | |
| Όγκος |
Η δίεδρη γωνία του κανονικού οκταέδρου είναι ίση με 109,47122°.
Το δυϊκό πολύεδρο του οκταέδρου είναι ο κύβος, δηλαδή τα κέντρα των οκτώ τριγωνικών εδρών του οκταέδρου αποτελούν κορυφές κύβου. Βεβαίως, ισχύει και το αντίστροφο, δηλαδή τα κέντρα των έξι εδρών του κύβου αποτελούν κορυφές οκταέδρου. Τόσο το οκτάεδρο όσο και ο κύβος ανήκουν στην ίδια ομάδα συμμετρίας, την οκταεδρική.
Το οκτάεδρο μπορεί να θεωρηθεί και ως τριγωνικό αντιπρίσμα, αποτελώντας έτσι το πρώτο μέλος της άπειρης σειράς των αντιπρισμάτων.
Επίσης, το οκτάεδρο μπορεί να θεωρηθεί και ως δύο τετραγωνικές πυραμίδες, που έχουν κοινή τη βάση τους (σε αυτή την περίπτωση το στερεό ονομάζεται τετραγωνική διπυραμίδα).
Αλγεβρική μορφή[Επεξεργασία | επεξεργασία κώδικα]
Το οκτάεδρο στο παραμετρικό σύστημα συντεταγμένων
0≤≤π
0≤≤(2π)
Αν τότε επανάλαμβάνονται διαδοχικά.
σταθερά
Παραπομπή: commons:file:parametric system of coordinates.pdf
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
Πηγές[Επεξεργασία | επεξεργασία κώδικα]
- Weisstein, Eric W., Octaedron, MathWorld. (Αγγλικά)
| |||||||||||
| |||||||||||||||||













