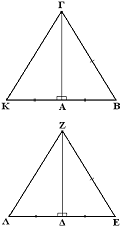
Ορθογώνιο τρίγωνο

Ορθογώνιο τρίγωνο με ορθή γωνία την Α. Η πλευρά $\alpha$ ονομάζεται υποτείνουσα και οι πλευρές $\beta$ και $\gamma$ είναι οι δύο κάθετες.

Στην γεωμετρία, ορθογώνιο τρίγωνο είναι το τρίγωνο του οποίου μία γωνία είναι ορθή. Οι πλευρές που περιέχουν την ορθή γωνία λέγονται κάθετες πλευρές και η απέναντί της λέγεται υποτείνουσα του ορθογώνιου τριγώνου.

Ιδιότητες

Ξεκινάμε με κάποιες βασικές ιδιότητες των ορθογωνίων τριγώνων:

• Οι οξείες γωνίες ορθογωνίου τριγώνου είναι συμπληρωματικές.
• Το εμβαδόν ενός ορθογωνίου τριγώνου είναι ίσο με το μισό του γινομένου των κάθετων πλευρών, δηλαδή

$\mathrm {E} ={\frac {1}{2}}\cdot \mathrm {AB} \cdot \mathrm {A\Gamma } .$

• Η διάμεσος ορθογωνίου τριγώνου που άγεται από την κορυφή της ορθής γωνίας ισούται με το μισό της υποτείνουσας και αντίστροφα.

Απόδειξη  

Η διάμεσος της ορθής γωνίας.

Απόδειξη ευθέος: Έστω $\mathrm {AB\Gamma }$ ένα ορθογώνιο τρίγωνο με την $\mathrm {A}$ ορθή, και $\mathrm {M}$ το μέσο της υποτείνουσας. Αν $\mathrm {\Delta }$ είναι το συμμετρικό του $\mathrm {A}$ ως προς το $\mathrm {M}$, τότε το $\mathrm {AB\Delta \Gamma }$ θα είναι ορθογώνιο παραλληλόγραμμο, ως τετράπλευρο με διχοτομούμενες διαγωνίους και μία ορθή γωνία. Άρα έχουμε $\mathrm {A\Delta } =\mathrm {B\Gamma }$, άρα $2\mathrm {AM} =\mathrm {B\Gamma }$, άρα $\mathrm {AM} =\mathrm {B\Gamma } /2$.

Απόδειξη αντίστροφου: Ας είναι $\mathrm {AB\Gamma }$ ένα τρίγωνο με διάμεσο $\mathrm {AM}$ τέτοια ώστε $\mathrm {AM} =\mathrm {B\Gamma } /2$. Αν $\mathrm {\Delta }$ είναι το συμμετρικό του $\mathrm {A}$ ως προς το $\mathrm {M}$, τότε το $\mathrm {AB\Delta \Gamma }$ είναι ορθογώνιο αφού οι διαγώνιοί του διχοτομούνται και είναι ίσες.

• Από αυτή την ιδιότητα προκύπτει ότι το μέσο της υποτείνουσας είναι το κέντρο του περιγεγραμμένου κύκλου, που έχει ακίνα $R={\tfrac {1}{2}}\mathrm {B\Gamma }$.

• Το ορθόκεντρο του τριγώνου ταυτίζεται με την κορυφή $\mathrm {A}$.
• Ο εγγεγραμμένος κύκλος του τριγώνου έχει ακτίνα ${\textstyle \rho ={\tfrac {\alpha +\beta -\gamma }{2}}={\tfrac {\beta \cdot \gamma }{\alpha +\beta +\gamma }}}$ και έγκεντρο του τριγώνου έχει συντεταγμένες $(\rho ,\rho )$ στο ορθοκανονικό σύστημα με αρχή το $\mathrm {A}$ και άξονες παράλληλους στις πλευρές $\mathrm {AB}$ και $\mathrm {A\Gamma }$.

Απόδειξη  

Το έγκεντρο του τριγώνου και ο διαχωρισμός του σε επιμέρους τρίγωνα.

Το εμβαδόν του ορθογωνίου τριγώνου δίνεται ως το άθροισμα των εμβαδών των τριγώνων $\mathrm {ABI}$, $\mathrm {A\Gamma I}$ και $\mathrm {B\Gamma I}$. Επομένως

${\frac {1}{2}}\cdot \mathrm {AB} \cdot \mathrm {A\Gamma } ={\frac {1}{2}}\cdot \mathrm {AB} \cdot \rho +{\frac {1}{2}}\cdot \mathrm {B\Gamma } \cdot \rho +{\frac {1}{2}}\cdot \mathrm {B\Gamma } \cdot \rho ={\frac {1}{2}}\cdot (\mathrm {AB} +\mathrm {B\Gamma } +\mathrm {B\Gamma } )\cdot \rho .$

Αναδιατάσσοντας τα δύο μέλη, λαμβάνουμε ότι

$\rho ={\frac {\mathrm {AB} \cdot \mathrm {A\Gamma } }{\mathrm {AB} +\mathrm {B\Gamma } +\mathrm {B\Gamma } }}={\frac {\beta +\gamma }{\alpha +\beta +\gamma }}.$

Τέλος για την πρώτη ισότητα, παρατηρήστε ότι

$(\alpha +\beta +\gamma )\cdot (\alpha +\beta -\gamma )=(\alpha +\beta )^{2}-\gamma ^{2}=\alpha ^{2}+\beta ^{2}+2\alpha \beta -\gamma ^{2}=2\alpha \beta ,$

χρησιμοποιώντας την διαφορά τετραγώνων και το Πυθαγόρειο θεώρημα.

Ο περιγεγραμμένος και ο εγγεγραμμένος κύκλος ορθογωνίου τριγώνου.

Μετρικές σχέσεις

Θεωρούμε το ορθογώνιο τρίγωνο $\mathrm {AB\Gamma }$ με ορθή την $\mathrm {A}$ και το ύψος $\mathrm {AA'}$ που αντιστοιχεί σε αυτή.

Τότε, ισχύουν οι εξής μετρικές σχέσεις:

• $\mathrm {AB} ^{2}=\mathrm {A'B} \cdot \mathrm {B\Gamma }$ και $\mathrm {A\Gamma } ^{2}=\mathrm {A'\Gamma } \cdot \mathrm {B\Gamma }$. Ισχύει και το αντίστροφο αν επιπλέον ${\hat {\mathrm {B} }}<90^{o}$ και ${\hat {\mathrm {\Gamma } }}<90^{o}$.

Απόδειξη  

Τα τρίγωνα $\mathrm {AB\Gamma }$ και $\mathrm {A'BA}$ είναι όμοια καθότι έχουν δύο γωνίες ίσες (την γωνία $B$ και μία ορθή). Επομένως,

${\frac {\mathrm {AB} }{\mathrm {A'B} }}={\frac {\mathrm {B\Gamma } }{\mathrm {AB} }}\quad \Rightarrow \mathrm {AB} ^{2}=\mathrm {A'B} \cdot \mathrm {B\Gamma } .$

Αντίστοιχα, τα τρίγωνα $\mathrm {AB\Gamma }$ και $\mathrm {A'\Gamma A}$ είναι όμοια. Επομένως,

${\frac {\mathrm {A\Gamma } }{\mathrm {A'\Gamma } }}={\frac {\mathrm {B\Gamma } }{\mathrm {A\Gamma } }}\quad \Rightarrow \mathrm {AB} ^{2}=\mathrm {A'B} \cdot \mathrm {B\Gamma } .$

• (Πυθαγόρειο Θεώρημα) $\mathrm {B\Gamma } ^{2}=\mathrm {AB} ^{2}+\mathrm {A\Gamma } ^{2}$ (ή αντίστοιχα $\alpha ^{2}=\beta ^{2}+\gamma ^{2}$). Ισχύει και το αντίστροφο.

Απόδειξη  

Από τις προηγούμενες δύο σχέσεις έχουμε ότι

$\mathrm {AB} ^{2}+\mathrm {A\Gamma } ^{2}=\mathrm {\mathrm {B} \Delta } \cdot \mathrm {\mathrm {B} \Gamma } +\mathrm {\Gamma \Delta } \cdot \mathrm {\mathrm {B} \Gamma } =(\mathrm {\mathrm {B} \Delta } +\mathrm {\Gamma \Delta } )\cdot \mathrm {\mathrm {B} \Gamma } =\mathrm {\mathrm {B} \Gamma } \cdot \mathrm {\mathrm {B} \Gamma } =\mathrm {\mathrm {B} \Gamma } ^{2}.$

• $u_{a}^{2}=\mathrm {AA'} ^{2}=\mathrm {BA'} \cdot \mathrm {\Gamma A'}$. Ισχύει και το αντίστροφο αν επιπλέον ${\hat {\mathrm {B} }}<90^{o}$ και ${\hat {\mathrm {\Gamma } }}<90^{o}$.

Απόδειξη  

Τα τρίγωνα $\mathrm {AA'B}$ και $\mathrm {AA'\Gamma }$ είναι όμοια, καθώς έχουν μία ορθή γωνία και δύο συμπληρωματικές. Επομένως,

${\frac {\mathrm {AA'} }{\mathrm {BA'} }}={\frac {\mathrm {\Gamma A'} }{\mathrm {AA'} }}\quad \Rightarrow \quad \mathrm {AA'} ^{2}=\mathrm {BA'} \cdot \mathrm {\Gamma A'} .$

• $\mathrm {AB} \cdot \mathrm {A\Gamma } =\mathrm {AA'} \cdot \mathrm {B\Gamma }$. Ισχύει και το αντίστροφο αν επιπλέον ${\hat {\mathrm {B} }}<90^{o}$ και ${\hat {\mathrm {\Gamma } }}<90^{o}$.

Απόδειξη  

Το εμβαδόν ενός τριγώνου δίνεται από τον τύπο

$\mathrm {E} ={\frac {1}{2}}\cdot ({\text{βάση}})\cdot ({\text{ύψος}}).$

Επομένως,

${\frac {1}{2}}\cdot \mathrm {AB} \cdot \mathrm {A\Gamma } ={\frac {1}{2}}\cdot \mathrm {AA'} \cdot \mathrm {B\Gamma } \quad \Rightarrow \quad \mathrm {AB} \cdot \mathrm {A\Gamma } =\mathrm {AA'} \cdot \mathrm {B\Gamma } .$

• ${\frac {1}{\mathrm {A} \mathrm {B} ^{2}}}+{\frac {1}{\mathrm {A} \Gamma ^{2}}}={\frac {1}{\mathrm {AA'} ^{2}}}$. Ισχύει και το αντίστροφο αν επιπλέον ${\hat {\mathrm {B} }}<90^{o}$ και ${\hat {\mathrm {\Gamma } }}<90^{o}$.

Απόδειξη  

${\frac {1}{\mathrm {AB} ^{2}}}+{\frac {1}{\mathrm {A\Gamma } ^{2}}}={\frac {\mathrm {AB} ^{2}+\mathrm {A\Gamma } ^{2}}{\mathrm {AB} ^{2}\cdot \mathrm {A\Gamma } ^{2}}}={\frac {\mathrm {B\Gamma } ^{2}}{\mathrm {AB} ^{2}\cdot \mathrm {A\Gamma } ^{2}}}={\frac {\mathrm {B\Gamma } ^{2}}{(\mathrm {AA'} \cdot \mathrm {B\Gamma } )^{2}}}={\frac {1}{\mathrm {AA'} ^{2}}}.$

Κριτήρια ισότητας ορθογώνιων τριγώνων

Ακολουθούν τα κριτήρια ισότητας ορθογωνίων τριγώνων:

• Κριτήριο πλευράς-πλευράς: Αν δύο ορθογώνια τρίγωνα έχουν δύο αντίστοιχες πλευρές τους ίσες μία προς μία τότε είναι ίσα.

Απόδειξη  

Κριτήριο πλευράς-πλευράς.

Διακρίνουμε δύο περιπτώσεις:

• Έχουν δύο κάθετες πλευρές ίσες. Στην περίπτωση αυτή θα είναι ίσα από το κριτήριο πλευράς-γωνίας-πλευράς, με δύο πλευρές ίσες μία προς μία και την περιεχόμενη γωνία ίση ως ορθή.

• Έχουν μία κάθετη πλευρά ίση και την υποτείνουσα. Αρκεί να δείξουμε ότι οι αντίστοιχες περιεχόμενες (οξείες) γωνίες θα είναι ίσες και τότε από το κριτήριο πλευράς-γωνίας-πλευράς θα είναι ίσα. Έστω λοιπόν δύο ορθογώνια τρίγωνα $\mathrm {AB\Gamma }$ και $\mathrm {\Delta EZ}$, τέτοια ώστε ${\hat {\mathrm {A} }}={\hat {\mathrm {\Delta } }}=90^{o}$, $\mathrm {AB} =\mathrm {\Delta E}$ και $\mathrm {B\Gamma } =\mathrm {EZ}$ (η ορθή γωνία σε κάθε τρίγωνο δεν μπορεί να είναι περιεχόμενη της κάθετης και της υποτείνουσας). Αρκεί να δείξουμε ότι ${\hat {B}}={\hat {E}}$ (ισότητα γωνιών). Στις προεκτάσεις των $\mathrm {AB}$ και $\mathrm {\Delta E}$ προς τα $\mathrm {A}$ και $\mathrm {\Delta }$, παίρνουμε σημεία $K$ και $\Lambda$ τέτοια ώστε $\mathrm {AK} =\mathrm {AB}$ και $\mathrm {\Delta \Lambda } =\mathrm {\Delta E}$ αντίστοιχα. Από το κριτήριο πλευράς-γωνίας-πλευράς έχουμε τις ισότητες του $\mathrm {AB\Gamma }$ με το $\mathrm {AK\Gamma }$ και του $\mathrm {\Delta EZ}$ με το $\mathrm {\Delta \Lambda Z}$. Συνεπώς έχουμε $\mathrm {K\Gamma } =\mathrm {B\Gamma } =\mathrm {EZ} =\mathrm {\Lambda Z}$. Από το κριτήριο πλευράς-πλευράς-πλευράς τότε τα τρίγωνα $\mathrm {\Gamma KB}$ και $\mathrm {Z\Lambda E}$ είναι ίσα, από όπου έχουμε ${\hat {B}}={\hat {E}}$ (ισότητα γωνιών).

• Κριτήριο πλευράς-προσκείμενης οξείας: Αν δύο ορθογώνια τρίγωνα έχουν μία πλευρά και την προσκείμενη οξεία γωνία ίσα τότε είναι ίσα.

Απόδειξη  

Κριτήριο πλευράς-προσκείμενης οξείας.

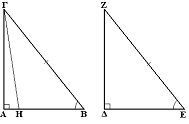Διακρίνουμε πάλι δύο περιπτώσεις:

• Έχουν μία κάθετη πλευρά και την προσκείμενη οξεία γωνία ίσα. Θα είναι ίσα από το κριτήριο γωνίας-πλευράς-γωνίας, με δύο γωνίες ίσες μία προς μία (η οξεία και η ορθή) και την περιεχόμενη κάθετη πλευρά ίση.
• Έχουν μία οξεία γωνία ίση και την υποτείνουσα. Έστω δύο τρίγωνα $\mathrm {AB\Gamma }$ και $\mathrm {\Delta EZ}$ με ${\hat {A}}={\hat {\Delta }}=90^{o}$, $\mathrm {B\Gamma } =\mathrm {EZ}$ και ${\hat {B}}={\hat {E}}$ (ισότητα γωνιών). Αρκεί να δείξουμε ότι $\mathrm {AB} =\mathrm {\Delta E}$. Θα το δείξουμε με απαγωγή σε άτοπο: Υποθέτουμε ότι $\mathrm {AB} >\mathrm {\Delta E}$. Θα υπάρχει τότε στην $\mathrm {AB}$ σημείο $\mathrm {H}$ για το οποίο $\mathrm {BH} =\mathrm {\Delta E}$. Τότε από το κριτήριο πλευράς-γωνίας-πλευράς τα τρίγωνα $\mathrm {HB\Gamma }$ και $\mathrm {\Delta EZ}$ πρέπει να είναι ίσα και να είναι ${\hat {H}}={\hat {\Delta }}=90^{o}$. Αυτό είναι άτοπο αφού από σημείο ευθείας περνά μόνο μία κάθετη στην ευθεία.

Ειδικά ορθογώνια τρίγωνα

Με γωνίες 30° και 60°

Τρίγωνο με γωνίες 30° και 60°. Το $\mathrm {M}$ είναι το μέσο της υποτείνουσας.

Το ορθογώνιο τρίγωνο με γωνίες 30° και 60°, έχει τις εξής ιδιότητες:

• Η κάθετη πλευρά που αντιστοιχεί στην γωνία 60° είναι ίση με το μισό της υποτείνουσας.
• Το τρίγωνο $\mathrm {AMB}$ ειναι ισόπλευρο.
• Τα μήκη των πλευρών είναι ανάλογα στα $1$, ${\sqrt {3}}$ και $2$.

Ορθογώνιο και ισοσκελές

Ορθογώνιο και ισοσκελές τρίγωνο ΑΒΓ.

Το ισοσκελές ορθογώνιο τρίγωνο έχει τις εξής ιδιότητες:

• Οι προσκείμενες γωνίες είναι 45°.
• Η υποτείνουσα έχει μήκος $x{\sqrt {2}}$ αν $x$ το μήκος των δύο κάθετων πλευρών.
• Το εμβαδόν του είναι ${\tfrac {1}{2}}x^{2}$.
• Προκύπτει ως το μισό ενός τετραγώνου (το $\mathrm {AB\Delta \Gamma }$ στο σχήμα).

Τρίγωνο Κέπλερ

Τρίγωνο Κέπλερ με τα τετράγωνα των πλευρών.

Το Τρίγωνο του Κέπλερ είναι ένα ορθογώνιο τρίγωνο του οποίου τα μήκη των πλευρών είναι διαδοχικοί όροι μιας γεωμετρικής προόδου. Προκύπτει ότι τα μήκη των πλευρών του είναι ανάλογα ως προς τα $1$, ${\sqrt {\phi }}$ και $\phi$, όπου $\phi$ είναι ο χρυσός λόγος.

Περαιτέρω θέματα

Τριγωνομετρία

Ορθογώνιο τρίγωνο με γωνία $\phi$.

Το ορθογώνιο τρίγωνο χρησιμοποιείται στον ορισμό των τριγωνομετρικών συναρτήσεων της γωνίας $\phi$. Πιο συγκεκριμένα, για την γωνία $\phi \in (0,90^{o})$, ισχύει ότι

$\sin \phi ={\frac {\text{απέναντι κάθετη}}{\text{υποτείνουσα}}}$ και $\cos \phi ={\frac {\text{προσκείμενη κάθετη}}{\text{υποτείνουσα}}}$.

Σπείρα Θεόδωρου

Η σπείρα του Θεόδορου.

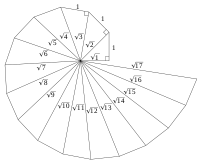
Η σπείρα του Θεόδορου είναι μία σπείρα που κατασκευάζεται από ορθογώνια τρίγωνα. Το πρώτο τρίγωνο είναι ένα ορθογώνιο και ισοσκελές τρίγωνο με κάθετη πλευρά μήκους $1$ (και υποτείνουσας μήκους ${\sqrt {2}}$). Το επόμενο τρίγωνο έχει μία κάθετη πλευρά την υποτείνουσα του πρώτου τριγώνου και άλλη κάθετη πλευρά μήκους $1$. Επομένως, έχει υποτεινουσα μήκους ${\sqrt {3}}$. Στην γενική περίπτωση, το $(n+1)$-οστό τρίγωνο έχει μία κάθετη πλευρά την υποτείνουσα του προηγούμενου τριγώνου και μία άλλη μήκους $1$. Επαγωγικά προκύπτει ότι το μήκος της υποτείνουσάς του είναι

${\textstyle {\sqrt {{\sqrt {n}}^{2}+1^{2}}}={\sqrt {n+1}}}$.

Πλακοστρώσεις

Τμήμα της πλακόστρωσης pinwheel.

Τα ορθογώνια τρίγωνα μπορούν να χρησιμοποιηθούν σε πλακοστρώσεις του επιπέδου. Για παράδειγμα, η πλακόστρωση pinwheel δίνει έναν μη-περιοδικό τρόπο να πλακοστρωθεί το επίπεδο.

Πυθαγόρειες τριάδες

Πυθαγόρειες τριάδες ονομάζονται οι τριάδες ακεραίων αριθμών $(a,b,c)$ τέτοιες ώστε

$c^{2}=a^{2}+b^{2}$.

Περαιτέρω ανάγνωση

Εξωτερικοί σύνδεσμοι

• Διαδραστική εφαρμογή για την επίλυση ορθογωνίου τριγώνου
• Διαδραστική εφαρμογή για τις μετρικές σχέσεις σε ορθογώνιο τρίγωνο

Ελληνικά άρθρα

• Κηπουρός Χρήστος (1991). «Υπολογισμός στοιχείων ορθογωνίου τριγώνου». Ευκλείδης Β΄ (4): 21-24. http://www.hms.gr/apothema/?s=sa&i=3421. 

Ξενόγλωσσα άρθρα

• Domenico, Angelo Di (Ιουλίου 2005). «89.41 The golden ratio—the right triangle—and the arithmetic, geometric, and harmonic means». The Mathematical Gazette 89 (515): 261–261. doi:10.1017/S0025557200177769. https://archive.org/details/sim_mathematical-gazette_2005-07_89_515/page/261. 
• Brown, Peter G. (Μαρτίου 2011). «Rays in a right triangle». The Mathematical Gazette 95 (532): 126–127. doi:10.1017/S0025557200002552. https://archive.org/details/sim_mathematical-gazette_2011-03_95_532/page/126. 
• Darvasi, Gyula (2003). «A Unique Property of Right-Angled Triangles». The Mathematical Gazette 87 (508): 51-59. https://www.jstor.org/stable/3620564. 
• Hiroshi Okumura; Masayuki Watanabe (2006). «90.26 A Right Triangle Inscribed in a Similar Right Triangle». The Mathematical Gazette 90 (517): 138-141. https://www.jstor.org/stable/3621439. 
• Tien, Li C. (Απριλίου 2009). «Right Triangle». The Mathematical Intelligencer 31 (2): 50–50. doi:10.1007/s00283-009-9045-y. 

Δείτε επίσης

• Τρίγωνο
• Τριγωνομετρία
• Ορθογώνιο παραλληλόγραμμο
• Πυθαγόρεια τριάδα
• Ψεύδο-ορθογώνιο τρίγωνο