Χώρος Μπάναχ
Στα μαθηματικά, και πιο συγκεκριμένα στη συναρτησιακή ανάλυση, ένας χώρος Μπάναχ (προφορά: /ˈbanax/,) είναι ένας πλήρης νορμικός διανυσματικός χώρος. Έτσι, ένας χώρος Μπάναχ είναι ένας διανυσματικός χώρος με μια μετρική που επιτρέπει τον υπολογισμό του μήκος του διανύσματος και της απόστασης μεταξύ των διανυσμάτων και είναι πλήρης, με την έννοια ότι μια Κωσύ ακολουθία διανυσμάτων πάντα συγκλίνει σε ένα καλά ορισμένο όριο που είναι μέσα στο χώρο.
Οι χώροι Μπάναχ πήραν το όνομά τους από τον Πολωνό μαθηματικό Στέφαν Μπάναχ, ο οποίος εισήγαγε αυτή την έννοια και την μελέτησε συστηματικά από το 1920 έως το 1922, μαζί με τον Χανς Χαν και τον Έντουαρντ Χέλλυ.[1] Οι χώροι Μπάναχ αρχικά αναπτύχθηκαν από την μελέτη των συναρτησιακών χώρων από τον Χίλμπερτ, τον Φρεσέτ, και τον Ριτζ νωρίτερα τον ίδιο αιώνα. Οι χώροι Μπάναχ παίζουν κεντρικό ρόλο στη συναρτησιακή ανάλυση. Σε άλλους τομείς της ανάλυσης, οι χώροι υπό μελέτη είναι συχνά χώροι Μπάναχ.
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Ένας χώρος Μπάναχ είναι ένας διανυσματικός χώρος X πάνω από το πεδίο R των πραγματικών αριθμών, ή πάνω από το πεδίο C των μιγαδικών αριθμών, ο οποίος είναι εξοπλισμένος με μια νόρμα και ο οποίος είναι πλήρης με την εν λόγω νόρμα, δηλαδή, για κάθε Κωσύ ακολουθία {xn} στον X, υπάρχει ένα στοιχείο x στο X τέτοια ώστε
ή αντίστοιχα:
Η δομή του διανυσματικού χώρου μας επιτρέπει να συσχετίσουμε την συμπεριφορά των Cauchy ακολουθιών με αυτήν των σειρών διανυσμάτων που συγκλίνουν. Ένα νορμικός χώρος X είναι ένας χώρος Μπάναχ αν και μόνον αν κάθε απολύτως συγκλίνουσα σειρά στο X συγκλίνει,[2]
- συνεπάγεται ότι συγκλίνει στο
Η πληρότητα του νορμικού χώρου διατηρείται αν η νόρμα είναι να αντικατασταθεί από μια ισοδύναμη νόρμα.
Όλες οι νόρμες σε ένα πεπερασμένων διαστάσεων διανυσματικό χώρο είναι ισοδύναμες. Κάθε πεπερασμένης διάστασης νορμικός χώρος πάνω από το R ή το C είναι ένας χώρος Μπάναχ.[3]
Γενική θεωρία[Επεξεργασία | επεξεργασία κώδικα]
Γραμμικοί τελεστές, ισομορφισμοί[Επεξεργασία | επεξεργασία κώδικα]
Αν X και Y είναι νορμικοί χώροι πάνω από το ίδιο σώμα K, το σύνολο όλων των συνεχών K-γραμμικών απεικονίσεων T : X → Y συμβολίζεται με B(X, Y). Στους απειροδιάστατους χώρους, δεν είναι όλες οι γραμμικές απεικονίσεις συνεχείς. Μια γραμμική αντιστοίχιση από έναν νορμικό χώρο X σε έναν άλλο νορμικό χώρο είναι συνεχής αν και μόνο αν είναι φραγμένο στην κλειστή μπάλα του X. Έτσι, ο διανυσματικός χώρος B(X, Y) μπορεί να δώσει τον νορμικό τελέστη.
Για Y από ένα χώρο Μπάναχ, ο χώρος B(X, Y) είναι ένας Μπάναχ χώρος, όσον αφορά αυτήν την νόρμα.
Αν X είναι ένας Μπάναχ χώρος, ο χώρος B(X) = B(X, X) αποτελεί μια μοναδιαία Μπάναχ άλγεβρα , ο πολλαπλασιασμός συναρτήσεων δίνεται από τη σύνθεση γραμμικών απεικονίσεων.
Αν X και Y είναι νορμικοί χώροι, θα είναι ισόμορφοι νορμικοί χώροι , αν υπάρχει ένας γραμμικός ισομορφισμός T : X → Y τέτοιος ώστε T και η αντίστροφη απεικόνιση του T -1 να είναι συνεχείς. Αν μία από τους δύο χώρους X ή Y είναι πλήρης (ή αυτοπαθής,διαχωρίσιμος, κ. λπ.) τότε είναι και ο άλλος χώρος. Δύο νορμικοί χώροι X και Y είναι ισομετρικά ισόμορφοι αν επιπλέον η T είναι ισομετρία, δηλαδή, ||T(x)|| = ||x|| για κάθε x στο X. Η Μπάναχ-Μαζούρ απόσταση d(X, Y) μεταξύ δύο ισόμορφων αλλά όχι ισομετρικών χώρων X και Y δίνει μια μέτρηση για το πόσο οι δύο χώροι X και Y διαφέρουν.
Βασικές έννοιες[Επεξεργασία | επεξεργασία κώδικα]
Κάθε νορμικός χώρος X μπορεί να ενσωματωθεί ισομετρικά σε ένα χώρο Μπάναχ. Πιο συγκεκριμένα, υπάρχει ένας χώρος Μπάναχ Y και μιαισομετρική απεικόνιση T : X → Y τέτοια ώστε T(X) να είναι πυκνό στο Y. Αν το Z είναι ένας άλλος Μπάναχ χώρος έτσι ώστε να υπάρχει ένας ισομετρικός ισομορφισμός από το X σε ένα πυκνό υποσύνολο του Z, τότε ο Z είναι ισομετρικά ισόμορφος με το Y.
Αυτός ο χώρος Μπάναχ Y είναι η πλήρωση του νορμικού χώρου X. Ο υποκείμενος μετρικός χώρος για Y είναι ο ίδιος με την μετρική πλήρωση του X, με την πράξη του διανυσματικού χώρου να επεκτείνεται από το X στο Y. Η πλήρωση του X συχνά συμβολίζεται με .
Το καρτεσιανό γινόμενο X × Y δύο νορμικών χώρων δεν είναι με κανονικό τρόπο εφοδιασμένο με μια νόρμα.Ωστόσο, πολλές ισοδύναμες νόρμες χρησιμοποιούνται συνήθως,[4] όπως
και αναπτύσσουν ισόμορφους νορμικούς χώρους. Με αυτή την έννοια, το γινόμενο X × Y (ή το ευθύ άθροισμα X ⊕ Y) είναι πλήρης αν και μόνο αν οι δύο παράγοντες είναι πλήρεις.
Αν M είναι κλειστός γραμμικός υποχώρος του νορμικού χώρου X, υπάρχει μια φυσική νόρμα πάνω στον χώρο πηλίκο X / M,
Το πηλίκο X / M είναι ένας Μπάναχ χώρος όταν το X είναι πλήρης.Η απεικόνιση πηλίκο από X σε X / M, που στέλνει το x από το X στην κλάση του x + M, είναι γραμμική, και έχει νόρμα 1, εκτός όταν M = X, στην περίπτωση αυτή το πηλίκο είναι το κενό διάστημα.
Ο κλειστός γραμμικός υποχώρος M του X λέγεται ότι είναι ένας συμπληρωματικός υποχώρος του X αν M είναι το πεδίο τιμών μιας φραγμένης γραμμικής προβολής P από X σε M. Σε αυτή την περίπτωση, ο χώρος X είναι ισόμορφος με το ευθύ άθροισμα των M και Ker(P), τον πυρήνα της προβολής P.
Ας υποθέσουμε ότι τα X και Y είναι χώροι Μπάναχ και T ∈ B(X, Y). Υπάρχει μια κανονική ανάλυση Τ ως[5]
όπου η πρώτη απεικόνιση d είναι η απεικόνιση πηλίκο , και η δεύτερη απεικόνιση T1 στέλνει κάθε κλάση x + Ker(T) του πηλίκου στην εικόνα T(x) στο Y. Η απεικόνιση είναι σαφώς καλά ορισμένη, επειδή όλα τα στοιχεία στην ίδια κλάση έχουν την ίδια εικόνα. Η απεικόνιση T1 είναι γραμμικός ισομορφισμός από X / Ker(T) πάνω στο πεδίο τιμών T(X), του οποίου το αντίστροφο δεν είναι ανάγκη να είναι φραγμένη.
Κλασικοί χώροι[Επεξεργασία | επεξεργασία κώδικα]
Βασικά παραδείγματα[6] των χώρων Μπάναχ περιλαμβάνουν:Lp χώρους και τις ειδικές περιπτώσεις τους, οι χώροι ακολουθιών ℓp που αποτελείται από αριθμητικές ακολουθίες με δείκτη από το σύνολο N ανάμεσά τους, ο χώρος ℓ1 των απολύτως αθροίσιμων ακολουθιών και το χώρο ℓ2 των τετραγωνικών αθροίσιμων ακολουθιών, το χώρο c0 των ακολουθιών που τείνουν στο μηδέν και το χώρο ℓ∞ των φραγμένων ακολουθιών; στο χώρο C(K) των αριθμητικών συναρτήσεων που είναι συνεχείς σε ένα συμπαγές Hausdorff χώρο K, που είναι εξοπλισμένος με την μέγιστη νόρμα,
Σύμφωνα με το Banach–Mazur θεώρημα, κάθε χώρος Μπάναχ είναι ισομετρικά ισόμορφοι με ένα υποχώρο κάποιου C(K).[7] Για κάθε διαχωρίσιμο χώρο Banach X, υπάρχει ένα κλειστό υποχώρο M της ℓ1 τέτοιο ώστε X ≅ ℓ1/M.[8]
Κάθε Hilbert χώρος χρησιμεύει ως ένα παράδειγμα ενός Μπάναχ χώρου. Ένας χώρος Χίλμπερτ Η πάνω στο K = R, C είναι πλήρης για μια νόρμα της μορφής
πού
είναι το εσωτερικό γινόμενο, γραμμικό στο πρώτο επιχείρημα που να πληροί τα παρακάτω:
Για παράδειγμα, ο χώρος L2 είναι ένα Χίλμπερτ χώρος.
Οι Χάρντι χώροι, οι χώροι Sobolev είναι παραδείγματα Μπάναχ χώρων που σχετίζονται με Lp χώρους και έχουν μια πρόσθετη δομή. Είναι σημαντικοί σε διάφορους κλάδους της ανάλυσης,στην Αρμονική ανάλυση και στις Μερικές διαφορικές εξισώσεις , μεταξύ άλλων.
Μπάναχ άλγεβρες[Επεξεργασία | επεξεργασία κώδικα]
Μια Μπάναχ άλγεβρα είναι ένας Μπάναχ χώρος A πάνω από το K = R ή C, μαζί με μια αλγεβρική δομή πάνω από το K,τέτοιο ώστε το γινόμενο των απεικονίσεων (a, b) ∈ A × A → ab ∈ A είναι συνεχής απεικόνιση. Μια ισοδύναμη νόρμα στο A μπορεί να βρεθεί, έτσι ώστε ||ab|| ≤ ||a|| ||b|| για όλα τα α, b ∈ A. α, β ∈ Α
Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]
- Ο χώρος Μπάναχ C(K), με το γινόμενο κατά σημεία, είναι μια άλγεβρα Μπάναχ.
- Ο δίσκος άλγεβρα A(D) αποτελείται από συναρτήσεις ολόμορφες στον ανοιχτό μοναδιαίο δίσκο D ⊂ C και συνεχής στο περίβλημα: D. Εξοπλισμένο με την μέγιστη νόρμα για την Δ, ο δίσκος άλγεβρα A(D) είναι μια κλειστή υποάλγεβρα C(D).
- Η Wiener άλγεβρα A(T) είναι η άλγεβρα των συναρτήσεων του μοναδιαίου κύκλου T που έχει κατά απόλυτη τιμή συγκλίνουσες σειρές Fourier. Μέσω τής απεικόνισης αντιστοιχούν μια συνάρτηση από το Τ στην ακολουθία των συντελεστών Fourier , αυτή η άλγεβρα είναι ισόμορφη προς την άλγεβρα Μπάναχ ℓ1(Z), όπου το γινόμενο είναι η συνέλιξη των ακολουθιών.
- Για κάθε χώρο Μπάναχ X, ο χώρος B(X) φραγμένου γραμμικού τελεστή σχετικά με το Χ, με την σύνθεση απεικονίσεων ως γινόμενο, είναι μια άλγεβρα Μπάναχ.
- Μία C*-άλγεβρα είναι μια μιγαδική άλγεβρα Μπάναχ Α με αυτοσυζυγή τελεστή ενέλιξη a → a∗ τέτοιο ώστε ||a∗a|| = ||α||2. Ο χώρος B(H) των φραγμένων γραμμικών τελεστών σε ένα χώρο Χίλμπερτ Η είναι ένα θεμελιώδες παράδειγμα της C*-άλγεβρα. Το Τζέλφαντ–Naimark θεώρημα ορίζει ότι κάθε C*-άλγεβρα είναι ισομετρικά ισόμορφη με μία C*-υποάλγεβρα κάποιων B(H). Ο χώρος C(K) των συνεχών μιγαδικών συναρτήσεων σε ένα συμπαγή Hausdorff χώρο K είναι ένα παράδειγμα αντιμεταθετικής C*-άλγεβρα, εφόσον η ενέλιξη τους αντιστοιχεί για κάθε συνάρτηση f την συζυγή συνάρτηση f .
Δυϊκός χώρος[Επεξεργασία | επεξεργασία κώδικα]
Αν X είναι ένας νορμικός χώρος και K το υποκείμενο πεδίο (είτε οι πραγματικοί ή οι μιγαδικοί αριθμοί), συνεχής δυϊκός χώρος είναι ο χώρος των συνεχών γραμμικών απεικονίσεων από X σε K, ή συνεχών γραμμικών συναρτήσεων. Ο συμβολισμός για τον συνεχή δυϊκό χώρο είναι X ' = B(X, K) σε αυτό το άρθρο.[9] Εφόσον το K είναι ένας Μπάναχ χώρος (με χρήση της απόλυτης τιμής ως νόρμα), ο δυϊκός X ' είναι ένας χώρος Μπάναχ, για κάθε νορμικό χώρο X.
Το κύριο εργαλείο για να αποδειχθεί η ύπαρξη συνεχούς γραμμικού συναρτησιακού είναι το Hahn–Banach θεώρημα.
- Hahn–Banach θεώρημα. Ας είναι το X ένας διανυσματικός χώρος πάνω από το πεδίο K = R, C. Ας είναι περαιτέρω
- Y ⊆ X είναι ένας γραμμικός υποχώρος,
- p : X → R είναι μια υπό-γραμμική συνάρτηση και
- f : Y → K είναι γραμμικό συναρτησιακό , ώστε Re( f (y)) ≤ p(y) για όλα τα y του Y.
- Στη συνέχεια, υπάρχει ένα γραμμικό συναρτησιακό F : X → K έτσι ώστε
Ειδικότερα, κάθε συνεχές γραμμικό συναρτησιακό σε έναν υποχώρο του νορμικού χώρου μπορεί να επεκτείνεται συνεχώς σε όλο το χώρο, χωρίς να αυξηθεί η νόρμα του συναρτησιακού.[10] Μια σημαντική ειδική περίπτωση είναι η εξής: για κάθε διάνυσμα x σε ένα νορμικό χώρο X, υπάρχει μία συνεχές γραμμικό λειτουργικό f στο X τέτοιο ώστε
Όταν το x είναι ίσο με το διάνυσμα 0 , το συναρτησιακό f πρέπει να έχει νόρμα ένα, και ονομάζεται νορμικό συναρτησιακό για το x.
Το Hahn–Banach θεώρημα διαχωρισμού αναφέρει ότι δύο ξένα μη-κενά κυρτά σύνολα σε ένα πραγματικό χώρο Μπάναχ, ένα από αυτά ανοιχτό, μπορεί να χωριστεί από ένα κλειστό συσχετισμένο υπερεπίπεδο. Το ανοιχτό κυρτό σύνολο κείται αυστηρά στη μία πλευρά του υπερεπιπέδου, το δεύτερο κυρτό σύνολο βρίσκεται στην άλλη πλευρά, αλλά μπορεί να αγγίξει το υπερεπίπεδο.[11]
Ένα υποσύνολο S σε ένα χώρο Μπάναχ X είναι ολικό εάν το γραμμικό περίβλημα του S είναι πυκνό στο X. Το υποσύνολο S είναι ολικό στο X αν και μόνο αν το μόνο συνεχές γραμμικό συναρτησιακό που χάνεται στο S είναι το 0 συναρτησιακό: αυτή η ισοδυναμία προκύπτει από το Hahn–Banach θεώρημα.
Αν X είναι το ευθύ άθροισμα δυο κλειστών γραμμικών υποχώρων M και N, τότε το διπλό X ' του X είναι ισόμορφος με το ευθύ άθροισμα των δυϊκών χώρων των M και N.[12] Εάν M είναι ένας κλειστός γραμμικός υποχώρος στο X, μπορεί να συνδεθεί το ορθογώνιο του M στον δυϊκό,
Ο ορθογώνιος M ⊥ είναι κλειστός γραμμικός υποχώρος του δυϊκού. Ο δυϊκός του M είναι ισομετρικά ισόμορφος με τον X ' / M ⊥. Ο δυϊκός του X / M είναι ισομετρικά ισόμορφος με το M ⊥.[13]
Τα δυϊκά του διαχωρίσιμου χώρου Μπάναχ δεν πρέπει να διαχωριστούν, αλλά:
- θεώρημα.[14] Ας είναι ο X είναι ένας νορμικός χώρος. Αν ο X ' είναι διαχωρίσιμος, τότε ο X είναι διαχωρίσιμος.
Όταν ο X ' είναι διαχωρίσιμος, το ανωτέρω κριτήριο για την ολικότητα μπορεί να χρησιμοποιηθεί για να αποδειχθεί η ύπαρξη ενός μετρήσιμου ολικού υποσυνόλου στο X.
Αδύναμες τοπολογίες[Επεξεργασία | επεξεργασία κώδικα]
Η αδύναμη τοπολογία σε ένα χώρο Μπάναχ X είναι η πιο τραχεία τοπολογία στο X για την οποία όλα τα στοιχεία x ' στον συνεχή δυϊκό χώρο X ' είναι συνεχή. Η τοπολογία της νόρμας, επομένως, είναι λεπτότερη από την αδύναμη τοπολογία. Όπως προκύπτει από το Hahn–Banach θεώρημα διαχωρισμού η αδύναμη τοπολογία είναι Hausdorff, και ότι ένα κλειστό κυρτό υποσύνολο με νόρμα από ένα χώρο Μπάναχ είναι επίσης ασθενώς κλειστό.[15] Μία νόρμα-συνεχής γραμμική απεικόνιση μεταξύ δύο χώρων Μπάναχ X και Y είναι επίσης ασθενώς συνεχής, δηλαδή, συνεχής από την αδύναμη τοπολογία του X, σε αυτήν της Y.[16]
Αν το X είναι άπειρων διαστάσεων, υπάρχουν γραμμικές απεικονίσεις που δεν είναι συνεχείς. Ο χώρος X∗ όλων των γραμμικών απεικονίσεων από το X στο υποκείμενο πεδίο K (αυτό το διάστημα X∗ ονομάζεταιαλγεβρικός διπλός χώρος, για να το διακρίνουν από τα X ') προκαλεί επίσης μια τοπολογία στο X η οποία είναι λεπτότερη από την αδύναμη τοπολογία, και χρησιμοποιείται πολύ λιγότερο στην συναρτησιακή ανάλυση.
Σε ένα δυϊκό χώρο X ', υπάρχει μια τοπολογία πιο αδύναμη από την αδύναμη τοπολογία του X ', που ονομάζεται αδύναμη* τοπολογία. Είναι η πιο τραχεία τοπολογία στο X ' , για την οποία όλες οι απεικονίσεις εκτιμητές x' ∈ X ' → x'(x), x ∈ X, είναι συνεχείς. Η σημασία της προέρχεται από το Banach–Alaoglu θεώρημα.
- Banach–Alaoglu Θεώρημα. Ας είναι το X ένας νορμικός διανυσματικός χώρος. Τότε η κλειστή μοναδιαία μπάλα B ' = {x' ∈ X ' : ||x'|| ≤ 1} του δυϊκού χώρου είναι συμπαγής στην αδύναμη* τοπολογία.
Το Banach–Alaoglu θεώρημα εξαρτάται από το θεώρημα του Tychonoff σχετικά με τα άπειρα γινόμενα των συμπαγή χώρων. Όταν ο X είναι διαχωρίσιμος, η μοναδιαία μπάλα B ' του δυϊκού είναι μετρικοποιήσιμη συμπαγής στην αδύναμη* τοπολογία.[17]
Παραδείγματα δυϊκών χώρων[Επεξεργασία | επεξεργασία κώδικα]
Ο δυϊκός του c0 είναι ισομετρικά ισόμορφος στο ℓ1:για κάθε φραγμένο γραμμικό συναρτησιακό f στο c0, υπάρχει ένα μοναδικό στοιχείο y = {yn} ∈ ℓ1 τέτοιο ώστε
Ο δυϊκός του ℓ1 είναι ισομετρικά ισόμορφος με τον ℓ∞.Ο δυϊκός του Lp([0, 1]) είναι ισομετρικά ισόμορφος με τον Lq([0, 1]) όταν 1 ≤ p < ∞ και 1p + 1q = 1.
Για κάθε διάνυσμα y σε ένα χώρο Χίλμπερτ H, η απεικόνιση
ορίζει ένα συνεχές γραμμικό συναρτησιακό fy στο H. Το θεώρημα εκπροσώπησης του Ρίτζ ορίζει ότι κάθε συνεχές γραμμικό συναρτησιακό Η είναι της μορφής fy για ένα μοναδικά ορισμένο διάνυσμα y στο Η. Η απεικόνιση y ∈ H → fy είναι μια αντιγραμμική ισομετρική αμφιμονοσήμαντη απεικόνιση από Η σε δυϊκό H '. Όταν οι αριθμητικές τιμές είναι πραγματικοί αριθμοί, αυτη η απεικόνιση είναι ένας ισομετρικός ισομορφισμός.
Όταν το K είναι συμπαγές Hausdorff τοπολογικός χώρος, ο δυϊκός M(K) της C(K) είναι ο χώρος του Ραδονίου μέτρου κατά την έννοια του Μπουρμπακί.[18] Το υποσύνολο P(K) του M(K) αποτελείται από μη αρνητικά μέτρα μάζας 1 ( μέτρα πιθανότητας) είναι μια κυρτή w*-κλειστή υποομάδα της μοναδιαίας μπάλας του M(K). Τα ακραία σημεία του P(K) είναι τα Dirac μέτρα για την Κ. Το σύνολο των Dirac μέτρων K, που είναι εξοπλισμένα με την w*-τοπολογία, είναι ομοιόμορφα με το K.
- Μπάναχ-Στόουν Θεώρημα. Αν K και L είναι συμπαγείς Hausdorff χώροι και αν C(K) και C(L) είναι ισομετρικά ισόμορφοι, τότε η τοπολογικοί χώρόι K και L είναιομοιόμορφα.[19][20]
Το αποτέλεσμα επεκτάθηκε από τον Αμίρ[21] και τον Κάμπερν[22] και για την περίπτωση που η πολλαπλασιαστική Banach–Mazur απόσταση μεταξύ των C(K) και C(L) είναι < 2. Το θεώρημα δεν ισχύει πλέον, όταν η απόσταση είναι = 2.[23]
Στην αντιμεταθετική άλγεβρα Banach C(K), τα μέγιστη ιδεώδη είναι ακριβώς πυρήνες των Dirac μέτρων για K,
Γενικότερα, από το Τζέλφαντ-Mazur θεώρημα, τα μέγιστη ιδεώδη της μοναδιαίας αντιμεταθετικής άλγεβρας Banach μπορούν να ταυτιστούν με τους χαρακτήρες της ---όχι απλώς ως σύνολα, αλλά ως τοπολογικοί χώροι: τα πρώτα με την τοπολογία περιβλήματος-πυρήνα και το τελευταίο με τη w*-τοπολογία. Σε αυτή την ταύτιση, το μέγιστο ιδεώδες χώρος μπορεί να θεωρηθεί ως ένα w*-συμπαγές υποσύνολο της μοναδιαίας μπάλας στο δυϊκό Α '.
- θεώρημα. Αν K είναι ένας συμπαγές Hausdorff χώρος, τότε το μέγιστο ιδεώδες χώρος Ξ της Μπάναχ άλγεβρα C(K) είναι ομοιόμορφο με το K.[19]
Δεν είναι κάθε μοναδιαία αντιμεταθετική άλγεβρα Μπάναχ της μορφής C(K) για κάποιο συμπαγές Hausdorff χώρο K. Ωστόσο, αυτή η δήλωση ισχύει αν κάποιος τοποθετήσει το Γ(K) στην μικρότερη κατηγορία των αντιμεταθετικών C*-αλγεβρών. Η αναπαράσταση του Τζέλφαντ είναι θεώρημα για τις αντιμεταθετικές C*-άλγεβρες που ορίζει ότι κάθε αντιμεταθετική μοναδιαία C*-άλγεβρα A είναι ισομετρικά ισόμορφη με ένα C(K) χώρο.[24] Ο Hausdorff συμπαγής χώρος Κ εδώ είναι και πάλι το μέγιστο ιδεώδες χώρος, που ονομάζεται επίσης το φάσμα του A στο πλαίσιο της C*-άλγεβρας.
Διαδυϊκός[Επεξεργασία | επεξεργασία κώδικα]
Αν X είναι ένα νορμικός χώρος, ο(συνεχής) δυϊκός X " του δυϊκού X ' ονομάζεται διαδυϊκός, ή ο δεύτερο δυϊκός της X. Για κάθε νορμικό χώρο X, υπάρχει μια φυσική απεικόνιση
Αυτό ορίζει την FX(x) να είναι ένα συνεχές γραμμικό συναρτησιακό Χ ', δηλαδή, ένα στοιχείο του X ". Ο χάρτης FX : x → FX(x) είναι μια γραμμική απεικόνιση από X σε X ". Κατά συνέπεια, η ύπαρξη νορμικού συναρτησιακού f για κάθε x στο X,η απεικόνιση FX είναι ισομετρική, έτσι ένεση.
Για παράδειγμα,το δυϊκό του X = c0 ταυτίζεται με το ℓ1, και το δυϊκό του ℓ1 ταυτίζεται με το ℓ∞,ο χώρος των φραγμένων αριθμητικών ακολουθιών. Ύστερα από αυτές τις ταυτίσεις, FX είναι απεικόνιση εγκλεισμού από το c0 στο ℓ∞. Είναι πράγματι ισομετρική,αλλά όχι από πάνω.
Αν η FX είναι έφεση, τότε ο νορμικός χώρος X ονομάζεται ανακλαστικό (βλ.παρακάτω). Είναι το δυϊκό του νορμικού χώρου, ο διαδυϊκός X " είναι πλήρης, ως εκ τούτου, κάθε ανακλαστικός νορμικός χώρος είναι ένας χώρος Μπάναχ.
Χρησιμοποιώντας την ισομετρική ενσωμάτωση FX, συνηθίζεται να εξετάζεται ένας νορμικός χώρος X ως ένα υποσύνολο του διαδυϊκού. Όταν το X είναι ένας Μπάναχ χώρος, που θεωρείται ως ένας κλειστός γραμμικός υποχώρος του X ". Αν το X δεν είναι ανακλαστικός, η μοναδιαία μπάλα του X είναι ένα κατάλληλο υποσύνολο της μοναδιαίας μπάλας του X ". Το Goldstine θεώρημα αναφέρει ότι η μοναδιαία μπάλα του νορμικού χώρου είναι ασθενώς*-πυκνή στη μοναδιαία μπάλα του bidual. Με άλλα λόγια, για κάθε x " στον διαδυϊκό, υπάρχει ένα καθαρό {xj} στον X ώστε
Το καθαρό στοιχείο μπορεί να αντικατασταθεί από μια ασθενώς*-συγκλίνουσα ακολουθία, όταν ο δυϊκός της X ′ είναι διαχωρίσιμος.Από την άλλη πλευρά, τα στοιχεία της διαδυϊκής ℓ1 τα οποία δεν περιέχονται στο ℓ1 δεν μπορούν να είναι ασθενή-όρια ακολουθιών του ℓ1, από την στιγμή που το ℓ1 είναι ασθενώς ακολουθιακά πλήρες.
Θεωρήματα Μπάναχ[Επεξεργασία | επεξεργασία κώδικα]
Εδώ είναι τα κύρια γενικά αποτελέσματα για Μπάναχ χώρους που πηγάζουν από το βιβλίο του Μπάναχ (Banach (1932)) και σχετίζονται με την κατηγορία Μπαίρ . Σύμφωνα με αυτό το θεώρημα,ένας πλήρης μετρικός χώρος (όπως ένας χώρος Banach,ένας χώρος Φρεσέτ ή ένας F-χώρος) δεν μπορεί να είναι ίσος με την ένωση των μετρήσιμων πολλαπλών κλειστών υποσυνόλων με κενό εσωτερικό σύνολο . Ως εκ τούτου, ένας χώρος Μπάναχ δεν είναι η ένωση των μετρήσιμων πολλαπλών κλειστών υποχώρων, εκτός αν είναι ήδη ίσος με έναν από αυτούς , ένας χώρος Μπάναχ με μια αριθμήσιμη Hamel βάση είναι πεπερασμένων διαστάσεων.
- Μπάναχ–Σταινχάους Θεώρημα. Ας το X είναι ένας Μπάναχ χώρος και Y είναι νορμικός διανυσματικός χώρος. Ας υποθέσουμε ότι η F είναι μια συλλογή των συνεχών γραμμικών τελεστών από X σε Y. Η αρχή του ομοιόμορφα φραγμένου δηλώνει ότι αν για όλα τα x στο X έχουμε supT∈F ||T(x)||Y < ∞, τότε supT∈F ||T||Y < ∞.
Το Μπάναχ–Σταινχάους Θεώρημα δεν περιορίζεται σε χώρους Μπάναχ. Μπορεί να επεκταθεί, για παράδειγμα, για την περίπτωση όπου το X είναι ένας Φρεσέτ χώρος, με την προϋπόθεση ότι η σύναψη τροποποιείται ως εξής: κάτω από την ίδια υπόθεση, υπάρχει μια γειτονία U του 0 στον X τέτοια ώστε όλα τα T στο F να είναι ομοιόμορφα φραγμένα στο U,
- Η Ανοικτή Απεικόνιση. Ας είναι X και Y χώροι Μπάναχ και T : X → Y να είναι ένας συνεχής γραμμικός τελεστής. Τότε, T είναι έφεση αν και μόνο αν T είναι μια ανοιχτή απεικόνιση.
- Πόρισμα. Κάθε ένας-προς-έναν φραγμένος γραμμικός τελεστής από ένα χώρο Μπάναχ σε ένα χώρο Μπάναχ είναι ένας ισομορφισμός.
- Το πρώτο Θεώρημα Ισομορφισμού για τους Μπάναχ χώρους. Υποθέτουμε ότι X και Y είναι χώροι Μπάναχ και ότι το T ∈ B(X, Y). Υποθέτουμε εν συνεχεία ότι το πεδίο τιμών του T είναι κλειστό στο Y. Τότε το X/ Ker(T) είναι ισόμορφο με το T(X).
Αυτό το αποτέλεσμα είναι άμεση συνέπεια του προηγούμενου Μπάναχ θεωρήματος ισομορφισμού και της κανονικής ανάλυσης φραγμένης γραμμικής απεικόνισης.
- Πόρισμα. Αν ένας χώρος Μπάναχ X είναι το εσωτερικό ευθύ άθροισμα των κλειστών υποχώρων M1, ..., Mn, τότε X είναι ισόμορφος με M1 ⊕ ... ⊕ Mn.
Αυτό είναι μια άλλη συνέπεια του Μπάναχ θεωρήματος ισομορφισμού, που εφαρμόζεται στην συνεχής bijection από M1 ⊕ ... ⊕ Mn στον X στέλνοντας τα (m1, ..., mn) στο άθροισμα m1 + ... + mn.
- Το Θεώρημα Κλειστού Γραφήματος . Ας είναι T : X → Y μια γραμμική αντιστοίχιση μεταξύ χώρων Μπάναχ. Το γράφημα του T είναι κλειστό στο X × Y αν και μόνο αν T είναι συνεχής.
Ανακλαστικότητα[Επεξεργασία | επεξεργασία κώδικα]
Ο νορμικός χώρος X ονομάζεται ανακλαστικός , όταν η φυσική απεικόνιση
είναι έφεση. Ανακλαστικοί νορμικοί χώροι είναι χώροι Μπάναχ.
- Θεώρημα. Αν X είναι ένας ανακλαστικός χώρος Μπάναχ, κάθε κλειστό υποσύνολο του X και κάθε χώρος πηλίκο X είναι ανακλαστικοί.
Αυτό είναι συνέπεια του Χανν–Μπάναχ θεωρήματος. Περαιτέρω, από το θεώρημα ανοιχτής απεικόνισης , αν υπάρχει ένας φραγμένος γραμμικός τελεστής από τον Μπάναχ χώρο X στον Μπάναχ χώρο Y, τότε ο Y είναι ανακλαστικός.
- Θεώρημα. Αν X είναι ένας Μπάναχ χώρος, τότε ο X είναι ανακλαστικός αν και μόνο αν ο X ' είναι ανακλαστικός.
- Πόρισμα. Ας είναι ο X ένας ανακλαστικός χώρος Μπάναχ. Τότε το X είναι διαχωρίσιμος , αν και μόνο αν ο X ' είναι διαχωρίσιμος.
Πράγματι, αν ο δυϊκός του Y ' ενός Μπάναχ χώρου Y είναι διαχωρίσιμος, τότε ο Y είναι διαχωρίσιμος. Αν ο X είναι ανακλαστικός και διαχωρίσιμος, τότε ο δυϊκός του X ' είναι διαχωρίσιμος, οπότε και ο X ' είναι διαχωρίσιμος.
- Θεώρημα. Ας υποθέσουμε ότι X1, ..., Xn είναι νορμικοί χώροι και ότι X = X1 ⊕ ... ⊕ Xn. Τότε το X είναι ανακλαστικό αν και μόνο αν κάθε Xj είναι ανακλαστικός.
Οι χίλμπερτ χώροι είναι ανακλαστικοί. Οι Lp χώροι είναι ανακλαστικοί όταν 1 < p < ∞. Γενικότερα, οι ομοιόμορφα κυρτοί χώροι είναι ανακλαστικοί, από το Μίλμαν-Πέττις θεώρημα. Οι χώροι c0, ℓ1, L1([0, 1]), C([0, 1]) δεν είναι ανακλαστικοί. Σε αυτά τα παραδείγματα μη-ανακλαστικών χώρων X, ο διαδυϊκός του X " είναι "πολύ μεγαλύτερος" από το X. Δηλαδή, υπό την φυσική ισομετρική ενσωμάτωση του X στο X " που δίνεται από το θεώρημα Χανν-Μπάναχ, το πηλίκο X " / X είναι άπειρων διαστάσεων, και ακόμη μη διαχωρίσιμο. Ωστόσο, ο Ρομπερτ Κ. Τζέιμς έχει κατασκευάσει ένα παράδειγμα[25] έναν μη-ανακλαστικό χώρο, που συνήθως ονομάζεται "οχώρος του Τζέιμς" και συμβολίζεται με J,[26] τέτοιον ώστε το πηλίκο J " / J είναι μονοδιάστατος χώρος. Επιπλέον, αυτό το διάστημα J είναι ισομετρικά ισόμορφο με τον διαδυϊκό.
- Θεώρημα. Ένας χώρο Μπάναχ X είναι ανακλαστικος αν και μόνο αν η μοναδιαία μπάλα είναι συμπαγής στην ασθενή τοπολογία
Όταν ο X είναι αντανακλαστικός, προκύπτει ότι όλα τα κλειστά και φραγμένα κυρτά υποσύνολα του X είναι ασθενώς συμπαγή. Σε ένα χώρο Χίλμπερτ H, η ασθενής συμπύκνωση της μοναδιαίας μπάλας χρησιμοποιείται πολύ συχνά με τον ακόλουθο τρόπο: κάθε φραγμένη ακολουθία στο Η έχει ασθενώς συγκλίνουσα υπακολουθία.
Η ασθενής συμπύκνωση της μοναδιαίας μπάλα παρέχει ένα εργαλείο για την εξεύρεση λύσεων σε αντανακλαστικούς χώρους σε ορισμένα προβλήματα βελτιστοποίησης. Για παράδειγμα, κάθε κυρτή συνεχής συνάρτηση της μοναδιαίας μπάλας B από ένα ανακλαστικό χώρο επιτυγχάνει το ελάχιστο σε κάποιο σημείο Β.
Ως ειδική περίπτωση του προηγούμενου αποτελέσματος , όταν ο X είναι ένας ανακλαστικός χώρος πάνω από το R, κάθε συνεχές γραμμικό συναρτησιακό f στο X "που φθάνει τη μέγιστη || f || στη μοναδιαία μπάλα του X. Το ακόλουθο θέωρημα του Ρόμπερτ Κ.Τζέιμς παρέχει μια αντίστροφη πορεία.
- Ο Τζέιμς Θεώρημα. Για έναν Μπάναχ χώρο οι ακόλουθες δύο ιδιότητες είναι ισοδύναμες:
- ο X είναι ανακλαστικός.
- για όλα τα f στο X " υπάρχει x στο X με ||x|| ≤ 1, τέτοιο ώστε f (x) = || f ||.
Το θεώρημα μπορεί να επεκταθεί για να δώσει ένα χαρακτηρισμό των ασθενώς συμπαγών κυρτών συνόλων.
Για κάθε μη-ανακλαστικό Μπάναχ χώρο X, υπάρχούν συνεχή γραμμικά συναρτησιακά που δεν φέρουν νόρμα. Ωστόσο, το θεώρημα Μπίσοπ-Φέλπς[27] αναφέρει ότι τα συναρτησιακά που φέρουν νόρμα είναι νορμικά πυκνά στον δυϊκό X ' του X.
Ασθενής συγκλίσεις των ακολουθιών[Επεξεργασία | επεξεργασία κώδικα]
Μια ακολουθία {xn} σε έναν Μπάναχ χώρο X είναι ασθενώς συγκλίνουσα σε ένα διάνυσμα x ∈ X αν f (xn) συγκλίνει στην f (x) για κάθε συνεχές γραμμικό συναρτησιακό f στο διπλό X '. Η ακολουθία {xn} είναι ασθενώς Cauchy ακολουθία αν f (xn) συγκλίνει σε ένα αριθμητικό όριο L( f ), για κάθε f στον X '. Μια ακολουθία { fn } στον δυϊκό X ' είναι ασθενώς* συγκλίνουσα σε ένα συναρτησιακό f ∈ X ' αν fn (x) συγκλίνει στην f (x) για κάθε x του X. Ασθενώς Cauchy ακολουθίες, ασθενώς συγκλίνουσα και ασθενώς* συγκλίνουσες ακολουθίες είναι νορμικά φραγμένες, ως συνέπεια του Μπάναχ-Σταινχάους θεωρήματος.
Όταν η ακολουθία {xn} στον X είναι ασθενώς Cauchy ακολουθία, το παραπάνω όριο L ορίζει ένα φραγμένο γραμμικό συναρτησιακό στον δυϊκό X ', δηλαδή, το L ένα στοιχείο του διαδυϊκού του X, και το L είναι το όριο της {xn} η ασθενής*-τοπολογία του διαδυϊκού. Ο Μπάναχ χώρος X είναι ασθενώς ακολουθιακά πλήρης αν κάθε ασθενώς Cauchy ακολουθία είναι ασθενώς συγκλίνουσα στο X. Όπως προκύπτει από την προηγούμενη συζήτηση οι ανακλαστικοί χώροι είναι ασθενώς ακολουθιακά πλήρεις.
- Θεώρημα. [28] Για κάθε μέτρο μ, ο χώρος L1(μ) είναι ασθενώς ακολουθιακά πλήρης.
Μια ορθοκανονική ακολουθία σε ένα χώρο Χίλμπερτ είναι ένα απλό παράδειγμα μιας ασθενώς συγκλίνουσας ακολουθίας, με όριο ίσο με το μηδενικό διάνυσμα. Η μοναδιαία διάνυσμα βάση της ℓp, 1 < p < ∞, ή της c0, είναι ένα άλλο παράδειγμα μιας ασθενώς μηδενική ακολουθία, δηλαδή, μια ακολουθία που συγκλίνει ασθενώς στο μηδενικό διάνυσμα. Για κάθε ασθενώς μηδενική ακολουθία σε ένα Μπάναχ χώρο, υπάρχει μια ακολουθία κυρτών συνδυασμών διανυσμάτων από τη δοθείσα ακολουθία που είναι νορμικά-συγκλίνουσα στο 0 μηδενικό διάνυσμα.[29]
Η μοναδιαία διάνυσμα βάση του ℓ1 δεν είναι ασθενώς Cauchy. Ασθενώς Cauchy ακολουθίες στον ℓ1 είναι ασθενώς συγκλίνουσες, αφού L1-χώροι είναι ασθενώς ακολουθιακά πλήρεις. Στην πραγματικότητα, ασθενώς συγκλίνουσες ακολουθίες στον ℓ1 είναι νορμικά συγκλίνουσες.[30] Αυτό σημαίνει ότι ℓ1 ικανοποιεί την ιδιότητα του Σούαρ.
Τα αποτελέσματα που αφορούν το ℓ1[Επεξεργασία | επεξεργασία κώδικα]
Ασθενώς Cauchy ακολουθίες και η ℓ1 βάση είναι οι αντίθετες περιπτώσεις της διχοτόμησης που καθιερώθηκε από τα ακόλουθα ενδελεχή αποτελέσματα του Χ. Π. Ρόζενταλ.[31]
- Θεώρημα.[32] Ας είναι{xn} φραγμένη ακολουθία σε ένα Μπάναχ χώρο . Είτε {xn} έχει μια ασθενώς Cauchy υπακολουθία, ή δέχεται μια υπακολουθία ισοδύναμη με το συνήθες μοναδιαίο διάνυσμα βάση του ℓ1.
Ένα συμπλήρωμα σε αυτό το αποτέλεσμα οφείλεται στους Οντέλ και Ρόσενταλ (1975).
- Θεώρημα.[33] Ας είναι ο X είναι ένας διαχωρίσιμος Μπάναχ χώρος. Τα ακόλουθα είναι ισοδύναμα:
- Ο χώρος X δεν περιέχει κλειστό υποσύνολο ισόμορφο με το ℓ1.
- Κάθε στοιχείο του διαδυϊκού X " είναι το ασθενές*όριο της ακολουθίας {xn} στον X.
Από το θεώρημα του Γκολντστάιν, κάθε στοιχείο της μοναδιαίας μπάλας B " του X " είναι το ασθενές*-όριο σε ένα καθαρό σημείο στην μοναδιαία μπάλα του X. Όταν το X δεν περιέχει τον ℓ1, κάθε στοιχείο του B " είναι ασθενές*-όριο μιας ακολουθίας στη μοναδιαία μπάλα του X.[34]
Όταν ο Μπάναχ χώρος X είναι διαχωρίσιμος, η μοναδιαία μπάλα του δυϊκού X ', που είναι εφοδιασμένα με την ασθενή*-τοπολογία, είναι ένας μετρικοποιήσιμος συμπαγής χώρος K,[17] και για κάθε στοιχείο x " στο διαδυϊκό X " ορίζει μια φραγμένη συνάρτηση στο K:
Αυτή η συνάρτηση είναι συνεχής για την συμπαγή τοπολογία του K αν και μόνο αν x " είναι στην πραγματικότητα στο X, που θεωρείται ως υποσύνολο του X ". Ας υποθέσουμε, επιπλέον, για το υπόλοιπο της παραγράφου, ότι το X δεν περιέχει τον ℓ1 χώρο. Από το προηγούμενο αποτέλεσμα των Οντέλ και Ρόζενταλ, η συνάρτηση x " είναι το για K από μια ακολουθία {xn} ⊂ X συνεχών συναρτήσεων στο Κ, ως εκ τούτου, είναι ένα στο K. Η μοναδιαία μπάλα του διαδυικού είναι σημειακά συμπαγές υποσύνολο της πρώτης Baire κλάσης στο K.[35]
Ακολουθίες, αδύναμη και αδύναμη* συμπαγές[Επεξεργασία | επεξεργασία κώδικα]
Όταν ο X είναι διαχωρίσιμος, η μοναδιαία μπάλα του δυϊκού χώρου είναι ασθενώς*-συμπαγής από το Μπάναχ–Αλάογλου θεώρημα και μετρικοποιήσιμη για την ασθενή* τοπολογία,[17] ως εκ τούτου, κάθε φραγμένη ακολουθία στο δυϊκό έχει ασθενώς* συγκλίνουσες υπακολουθίες. Αυτό ισχύει για διαχωρίσιμους ανακλαστικούς χώρους, αλλά δεν είναι αλήθεια σε αυτή την περίπτωση, όπως αναφέρεται παρακάτω.
Η αδύναμη τοπολογία ένος Μπάναχ χώρου X είναι μετρικοποιήσιμη αν και μόνο αν το X είναι πεπερασμένων διαστάσεων.[36] Αν ο δυϊκός X ' είναι διαχωρίσιμος, η αδύναμη τοπολογία της μοναδιαίας μπάλας του X είναι μετρικοποιήσιμη. Αυτό ισχύει ιδίως για του διαχωρίσιμους ανακλαστικούς Μπάναχ χώρους. Αν και η ασθενής τοπολογία της μοναδιαίας μπάλας δεν είναι μετρικοποιήσιμη σε γενικές γραμμές, μπορεί κανείς να δείξει ασθενή πυκνότητα χρησιμοποιώντας ακολουθίες.
- Eberlein–Šmulian θεώρημα.[37] Ένα σύνολο Α σε έναν Μπάναχ χώρο είναι σχετικά ασθενώς συμπαγές αν και μόνο αν κάθε ακολουθία {αn} του Α έχει ασθενώς συγκλίνουσα υπακολουθία.
Ένας Μπάναχ χώρος X είναι ανακλαστικός αν και μόνο αν για κάθε φραγμένη ακολουθία στον X έχει ασθενώς συγκλίνουσα υπακολουθία.[38]
Ένα ασθενώς συμπαγές υποσύνολο Α στο ℓ1 είναι νορμικά-συμπαγές. Πράγματι, κάθε ακολουθία στο A έχει ασθενώς συγκλίνουσα υπακολουθία από Eberlein–Šmulian, που είναι νορμικά συγκλίνουσα από την ιδιότητα Schur του ℓ1
Βάσεις του Σάουντερ[Επεξεργασία | επεξεργασία κώδικα]
Μια βάση Σάουντερ σε έναν Μπάναχ χώρο X είναι μια ακολουθία {en}n ≥ 0 από διανύσματα του X με την ιδιότητα ότι για κάθε διάνυσμα x του X, υπάρχει μοναδικά ορισμένη αριθμητική ακολουθία {xn}n ≥ 0 εξαρτημένη από το x, έτσι ώστε
Μπάναχ χώροι με βάση Σάουντερ είναι απαραίτητα διαχωρίσιμες, επειδή το μετρήσιμο σύνολο των πεπερασμένων γραμμικών συνδυασμών με πραγματικούς συντελεστές (ας πούμε) είναι πυκνό.
Προκύπτει από το θεώρημα Μπάναχ–Στάινχαουζ ότι δηλαδή οι γραμμικές απεικονίσεις {Pn} είναι ομοιόμορφα φραγμένες από κάποια σταθερά C. Ας είναι η {e∗
n} να υποδηλώνει τα συναρτησιακά συντεταγμένες τα οποία στέλνουν κάθε x του X στη συντεταγμένη xn του x στην παραπάνω επέκταση. Αυτά λέγονται διορθογώνια συναρτησιακά. Όταν τα διανύσματα βάση έχουν νόρμα 1, τα συναρτησιακά συντεταγμένες {e∗
n} έχουν νόρμα ≤ 2C στο δυικο του X.
Οι πιο κλασικοί διαχωρίσιμοι χώροι έχουν ρητές βάσεις. Το σύστημα του Χάαρ {hn} είναι μια βάση για τον Lp([0, 1]), 1 ≤ p < ∞. Το τριγωνομετρικό σύστημα είναι μια βάση στον Lp(T) , όταν 1 < p < ∞. Το Σάουντερ σύστημα είναι μια βάση στο χώρο C([0, 1]).[39] Το ερώτημα για το αν ο δίσκος άλγεβρα A(D) έχει βάση[40] παρέμεινε ανοικτό για περισσότερα από σαράντα χρόνια, μέχρι που ο Bočkarev έδειξε το 1974 ότι A(D) επιδέχεται βάση κατασκευασμένη από το Φράνκλιν σύστημα.[41]
Εφόσον κάθε διάνυσμα x σε έναν Μπάναχ χώρο X με βάση είναι το όριο του Pn(x),οπου η Pn είναι πεπερασμένης τάξης και ομοιόμορφα φραγμένη, ο χώρος X ικανοποιεί την ιδιότητά φραγμένης προσέγγισης . Το πρώτο παράδειγμα[42] από τονΈνφλο ενός χώρου που δεν ικανοποιεί την ιδιότητα προσέγγισης ήταν ταυτόχρονα το πρώτο παράδειγμα ένα διαχωρίσιμου Μπάναχ χώρου χωρίς βάση Σάουντερ.
Ο Ρόμπερτ Κ. Τζέιμς χαρακτήρισε την ανακλαστικότητα σε Μπάναχ χώρους που περιέχουν βάση: ο χώρος X με βάση Σάουντερ είναι ανακλαστικός αν και μόνο αν η βάση είναι μαζί συσταλλόμενα και φραγμένα πλήρης[43] Σε αυτή την περίπτωση, τα διδιορθογώνια συναρτησιακά αποτελούν τη βάση του δυϊκού του X.
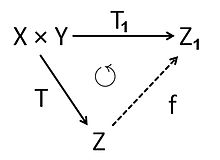
Τανυστικό γινόμενο[Επεξεργασία | επεξεργασία κώδικα]
Ας είναι X και Y είναι δύο K-διανυσματικοί χώροι. Το τανυστικό γινόμενο X ⊗ Y των X και Y είναι ένας K-διανυσματικός χώρος Z με μια διγραμμική απεικόνιση T : X × Y → Z που έχει την εξής καθολική ιδιότητα:
- Αν T1 : X × Y → Z1 είναι οποιαδήποτε διγραμμική απεικόνιση σε έναν K-διανυσματικό χώρο Z1, τότε υπάρχει μοναδική γραμμική απεικόνιση f : Z → Z1 τέτοια ώστε T1 = f ∘ T.
Η εικόνα κάτω από το T ενός ζεύγους (x, y) στο X × Y συμβολίζεται με x ⊗ y, και ονομάζεται απλός τανυστής. Κάθε στοιχείο z στο X ⊗ Y είναι ένα πεπερασμένο άθροισμα τέτοιων απλών τανυστών.
Υπάρχουν διάφορες νόρμες που μπορούν να τοποθετηθούν στο τανυστικό γινόμενο των υποκείμενων διανυσματικών χώρων, μεταξύ άλλων,η προβολική εγκάρσια νόρμα και η ερριπτική εγκάρσια νόρμα που εισήχθη από τον Α. Γκρότεντικ το 1955.[44]
Σε γενικές γραμμές, το τανυστικό γινόμενο τών πλήρεις χώρών δεν είναι πλήρης και πάλι. Όταν εργάζεστε με Μπάναχ χώρους, είναι σύνηθες ότι το προβολικό τανυστικό γινόμενο[45] δύο χώρων Μπάναχ X και Y είναι η πλήρωση του αλγεβρικού τανυστικού γινομένου X ⊗ Y εξοπλισμένο με την προβολική τανυστική νόρμα, και ομοίως για το ερριπτικό τανυστικό γινόμενο[46] . Ο Γκρότεντικ απέδειξε συγκεκριμένα ότι[47]
όπου K είναι ένας συμπαγές Hausdorff χώρος C(K, Y) ο Μπάναχ χώρος των συνεχών συναρτήσεων από το Κ προς Y και L1([0, 1], Y) είναι ο χώρος των Bochner-μετρήσιμων και ολοκληρώσιμων συναρτήσεων από το [0, 1] στο Y, και όπου οι ισομορφισμοί είναι ισομετρικοί. Οι δύο ισομορφισμοί παραπάνω είναι οι αντίστοιχες επεκτάσεις της απεικόνισης που στέλνει τον τανυστή f ⊗ y στην συνάρτηση που έχει τιμές διανύσματα s ∈ K → f (s)y ∈ Y.
Τανυστικά γινόμενα και η ιδιότητα προσέγγισης [Επεξεργασία | επεξεργασία κώδικα]
Ας είναι το X είναι ένας Μπάναχ χώρος. Το τανυστικό γινόμενο προσδιορίζεται ισομετρικά με το περίβλημα B(X) από το σύνολο των πεπερασμένης τάξης τελεστών. Όταν ο X έχει την ιδιότητα προσέγγισης, το περίβλημα αυτό συμπίπτει με το χώρο των συμπαγών τελεστών στον X.
Για κάθε χώρο Μπάναχ Y, υπάρχει μια φυσική νόρμα 1 γραμμική απεικόνιση
που λαμβάνεται με την επέκταση της ταυτοτικής απεικόνισης του αλγεβρικού τανυστικού γινομένου. Ο Γκρότεντικ που συνέδεσε το πρόβλημα της προσέγγισης με το ερώτημα για το αν αυτή η απεικόνιση είναι ένα-προς-ένα όταν ο Y είναι δυϊκός του X. Συγκεκριμένα, για κάθε Μπάναχ χώρο X, η απεικόνιση
είναι ένα-προς-ένα αν και μόνο αν ο X έχει την ιδιότητα προσέγγισης .[48]
Ο Γκρότεντικ εικάστηκε ότι και πρέπει να είναι διαφορετικά, όταν X και Y είναι άπειρων διαστάσεων Μπάναχ χώροι. Αυτό είχε διαψευστεί από τον Gilles Pisier το 1983.[49] Ο Pisier κατασκεύασε ένα άπειρων διαστάσεων χώρο Μπάναχ X τέτοιο ώστε και να είναι ίσες. Επιπλέον, όπως το παράδειγμα τουΈνφλο, αυτός ο χώρος X είναι ένας "χειροποίητος" χώρος που δεν έχει την ιδιότητα προσέγγισης. Από την άλλη πλευρά,ο Szankowski απέδειξε ότι ο κλασικός χώρος B(ℓ2) δεν έχει την ιδιότητα προσέγγιση.[50]
Μερική ταξινόμηση αποτελεσμάτων[Επεξεργασία | επεξεργασία κώδικα]
Χαρακτηρισμοί των Χίλμπερτ χώρων μεταξύ χώρων Μπάναχ [Επεξεργασία | επεξεργασία κώδικα]
Μια αναγκαία και επαρκή συνθήκη για την νόρμα ενός χώρο Μπάναχ X για να συνδεθεί με ένα εσωτερικό γινόμενο είναι ο νόμος του παραλληλογράμμου:
Ακολούθως, για παράδειγμα, ο Lebesgue χώρος Lp([0, 1]) είναι ένας χώρος Χίλμπερτ μόνο όταν p = 2. Αν αυτή η ταυτότητα ικανοποιείται, το σχετικό εσωτερικό γινόμενο δίνεται από την ταυτότητα πόλωσης. Στην περίπτωση που έχουμε πραγματικούς αριθμούς αυτό δίνει:
Για μιγαδικούς αριθμούς, ορίζουμε το εσωτερικό γινόμενο, ώστε να είναι C-γραμμικό ως προς x,και αντιγραμμικό στο y, η ταυτότητα πόλωσης δίνει:
Για να δείτε ότι ο νόμος του παραλληλογράμμου είναι επαρκής, παρατηρεί κανείς στην περίπτωση των πραγματικών αριθμών που < x, y > είναι συμμετρικό, και την περίπτωση των μιγαδικών, που πληροί την ιδιότητα της Ερμιτιανής συμμετρίας και < ix, y > = i < x, y >. Ο νόμος του παραλληλογράμμου υποδηλώνει ότι < x, y > είναι προσθετικό στο x. Επομένως, είναι γραμμική, πάνω από τους ρητούς, έτσι γραμμική από συνέχεια.
Διάφοροι χαρακτηρισμοί των ισόμορφων χώρων (αντί ισομετρικών) σε Χίλμπερτ χώρους είναι διαθέσιμοι. Ο νόμος του παραλληλόγραμμο μπορεί να επεκταθεί σε περισσότερα από δύο διανύσματα, και να αποδυναμωθεί από την εισαγωγή μιας διπλής ανισότητα με σταθερά c ≥ 1: Kwapień απέδειξε ότι αν
για κάθε ακέραιο n και όλες τις οικογένειες των διανυσμάτων {x1, ..., xn} ⊂ X, τότε ο χώρος Μπάναχ X είναι ισόμορφος με ένα χώρο Χίλμπερτ.[51] Εδώ, Ave± δηλώνει τον μέσο όρο των 2n πιθανών επιλογών προσήμων ±1. Στο ίδιο άρθρο,ο Kwapień αποδεικνύει ότι η ισχύς του θεωρήματος του Παρσέβαλ, που έχει τιμές Μπάναχ χώρους, για το μετασχηματισμό Fourier χαρακτηρίζει τους Μπάναχ χώρους ισόμορφους με Hilbert χώρους.
Lindenstrauss και Tzafriri απεδείξαν ότι ο χώρος Μπάναχ στον οποίο κάθε κλειστός γραμμικός υποχώρος είναι πληρωμένος (που είναι, το έυρος μιας φραγμένης γραμμικής προβολής) είναι ισόμορφος με ένα χώρο Χίλμπερτ.[52] Η απόδειξη στηρίζεται από στο θεώρημα του Dvoretzky για τα Ευκλείδεια τμήματα των μεγάλων διαστάσεων κεντρικά συμμετρικά κυρτά σώματα. Με άλλα λόγια, το θεώρημα του Dvoretzky αναφέρει ότι για κάθε ακέραιο n, κάθε πεπερασμένων διαστάσεων νορμικός χώρος, με διάσταση αρκετά μεγάλη σε σύγκριση με το n, περιέχει υπόχωρο σχεδόν ισομετρικό στο n-διάστατο Ευκλείδειο χώρο.
Το επόμενο αποτέλεσμα δίνει την λύση του λεγόμενου προβλήματος του ομοιογενή χώρου . Ένας άπειρων διαστάσεων Μπάναχ χώρος X είναι ομοιογενής αν είναι ισόμορφος με όλους τους απείρων διαστάσεων κλειστούς υποχώρους. Ένας Μπάναχ χώρος ισομορφος με το ℓ2 είναι ομοιογενής, και ο Μπάναχ αναρωτήθηκε για το αντίστροφο.[53]
- Θεώρημα.[54] Ένας χώρος Μπάναχ ισόμορφος με όλες τους απείρων διαστάσεων κλειστούς υποχώρους είναι ισόμορφος με έναν διαχωρίσιμο χώρο Χίλμπερτ.
Ένας άπειρο-διάστατος χώρος Μπάναχ είναι κληρονομικά αδιάσπαστος όταν κανένα υποχώρος του δεν μπορεί να είναι ισόμορφος με το ευθύ άθροισμα δύο άπειρο-διάστατων χώρων Μπάναχ. Το θεώρημα διχοτόμησης του Γκάουερ[54] υποστηρίζει ότι κάθε άπειρο-διάστατος χώρος Μπάναχ X περιέχει είτε έναν υποχώρο Y με αδέσμευτη βάση, είτε έναν κληρονομικά αδιάσπαστο υποχώρο Z, και ιδίως, Z δεν είναι ισόμορφος με τα κλειστά υπερεπίπεδά του.[55] Αν X είναι ομοιογενής,θα πρέπει τότε να έχει μια αδέσμευτη βάση. Συνεπάγεται επομένως, στη συνέχεια, από τη μερική λύση που λαμβάνεται από τον Komorowski και τον Tomczak–Jaegermann, για χώρους με μια αδέσμευτη βάση,[56] ότι X είναι ισόμορφος με τον ℓ2.
Χώροι συνεχών συναρτήσεων[Επεξεργασία | επεξεργασία κώδικα]
Όταν δύο συμπαγείς χώροι Hausdorff K1 και K2 είναι ομοιόμορφοι, οι χώρους Μπάναχ C(K1) και C(K2) είναι ισομετρικοί. Αντίθετα, όταν K1 δεν είναι ομοιόμορφος με K2, η (πολλαπλασιαστική) Μπάναχ-Μαζούρ απόσταση μεταξύ των C(K1) και C(K2) πρέπει να είναι μεγαλύτερη ή ίση με 2, βλέπε ανωτέρω τα αποτελέσματα από τον Αμίρ και τον Κάμπερν. Αν και οι μη μετρήσιμοι συμπαγείς μετρικοί χώροι μπορεί να έχουν διαφορετικά είδη ομοιομορφισμών, ο ένας έχει το ακόλουθο αποτέλεσμα χάρη στον Μιλούτιν:[57]
- Θεώρημα.[58] Ας είναι το K μη μετρήσιμος συμπαγής μετρικός χώρος. Τότε C(K) είναι ισόμορφος με C([0, 1]).
Η κατάσταση είναι διαφορετική για μετρήσιμα άπειρους συμπαγείς Hausdorff χώρους. Κάθε μετρήσιμα άπειρος συμπαγής K είναι ομοιόμορφος σε κάποιο κλειστό διάστημα των διατακτικών αριθμών
εξοπλισμένο με την διατεταγμένη τοπολογία, όπου α είναι μια μετρήσιμα άπειρη διάταξη.[59] Ο Μπάναχ χώρος C(K) είναι τότε ισομετρικός με C(<1, α >). Όταν α, β είναι δύο μετρήσιμα άπειροι διατακτικοί αριθμοί , και υποθέτοντας ότι α ≤ β, οι χώροι C(<1, α >) και C(<1, β >) είναι ισόμορφοι αν και μόνο αν β < αω.[60] Για παράδειγμα, οι χώροι Μπάναχ
είναι αμοιβαία μη-ισόμορφοι.
Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]
Ένα γλωσσάρι συμβόλων:
- K = R, C;
- X είναι έναςσυμπαγής Χάουσντορφ χώρος;
- Ιείναι ένα κλειστό και φραγμένο διάστημα [a, b];
- p, q είναι πραγματικοί αριθμοί 1 < p, q < ∞ τέτοιοι ώστε 1p + 1q = 1.
- Σ είναι μια σ-άλγεβρα από σύνολα;
- Ξ είναι μια άλγεβρα από σύνολα (για χώρους που χρειάζονται μόνο πεπερασμένη προσθετικότητα,όπως είναι ο ba χώρος);
- μ είναι μέτρο με μεταβολή |μ|.
| Κλασικοί Μπάναχ χώροι | |||||
| Δυϊκός χώρος | Ανακλαστικότητα | Ασθενώς ακολουθιακά Πλήρης | Νόρμα | Σημειώσεις | |
|---|---|---|---|---|---|
| Kn | Kn | Ναι | Ναι | Ευκλείδειος χώρος | |
| ℓn p |
ℓn q |
Ναι | Ναι | ||
| ℓn ∞ |
ℓn 1 |
Ναι | Ναι | ||
| ℓp | ℓq | Ναι | Ναι | ||
| ℓ1 | ℓ∞ | Όχι | Ναι | ||
| ℓ∞ | ba | Όχι | Όχι | ||
| c | ℓ1 | Όχι | Όχι | ||
| c0 | ℓ1 | Όχι | Όχι | Ισόμορφος αλλά όχι ισομετρικός με τον c. | |
| bv | ℓ∞ | Όχι | Ναι | Ισομετρικά ισόμορφος με τον ℓ1. | |
| bv0 | ℓ∞ | Όχι | Ναι | Ισομετρικά ισόμορφος με τον ℓ1. | |
| bs | ba | Όχι | Όχι | Ισομετρικά ισόμορφος με τον ℓ∞. | |
| cs | ℓ1 | Όχι | Όχι | Ισομετρικά ισόμορφος με τον c. | |
| B(X, Ξ) | ba(Ξ) | Όχι | Όχι | ||
| C(X) | rca(X) | Όχι | Όχι | ||
| ba(Ξ) | ? | Όχι | Ναι | ||
| ca(Σ) | ? | Όχι | Ναι | Κλειστός υποχώρος του ba(Σ). | |
| rca(Σ) | ? | Όχι | Ναι | Κλειστός υποχώρος του ca(Σ). | |
| Lp(μ) | Lq(μ) | Ναι | Ναι | ||
| L1(μ) | L∞(μ) | Όχι | Ναι | Ο δυϊκός είναι L∞(μ) αν μ είναι σ-πεπερασμένος. | |
| BV(I) | ? | Όχι | Ναι | Vf (I) είναι η ολική μεταβολή της f | |
| NBV(I) | ? | Όχι | Ναι | NBV(I) αποτελείται από BV(I) συναρτήσεις τέτοιες ώστε | |
| AC(I) | K + L∞(I) | Όχι | Ναι | Ισόμορφος με τον χώρο Σομπόλεφ W 1,1(I). | |
| Cn([a, b]) | rca([a,b]) | Όχι | Όχι | Ισόμορφος με τον Rn ⊕ C([a,b]),κάτ' ουσία από το θεώρημα Τέιλορ. | |
Παράγωγοι[Επεξεργασία | επεξεργασία κώδικα]
Αρκετές έννοιες μιας παραγώγου μπορούν να οριστούν σε ένα Μπάναχ χώρο . Δείτε τα άρθρα σχετικά με την παράγωγο Φρεσέτ και την παράγωγο του Gâteaux για λεπτομέρειες. Η παράγωγος Φρεσέτ επιτρέπει την επέκταση της έννοιας μιας κατευθυνόμενης παραγώγου σε χώρους Μπάναχ. Η παράγωγος του Gâteaux επιτρέπει την επέκταση μιας κατευθυνόμενης παραγώγου για τοπικά κυρτούς τοπολογικού διανυσματικούς χώρους. Η Φρεσέτ διαφορισιμότητα είναι ισχυρότερη συνθήκη από την Gâteaux διαφορισιμότητα. Η οιονεί παράγωγος είναι μια άλλη επέκταση των κατευθυνόμενων παράγωγων που υποδηλώνει μια ισχυρότερη συνθήκη από την Gâteaux διαφορισιμότητα, αλλά μια ασθενέστερη συνθήκη από την Φρεσέτ διαφορισιμότητα .
Επεκτάσεις[Επεξεργασία | επεξεργασία κώδικα]
Πολλοί σημαντικοί χώροι στην συναρτησιακή ανάλυση, για παράδειγμα ο χώρος όλων των απείρως και συχνά διαφορίσιμων συναρτήσεων R → R, ή ο χώρος όλων των κατανομών του R, είναι πλήρεις αλλά όχι νορμικοί διανυσματικοί χώροι και ως εκ τούτο όχι χώροι Μπάναχ. Στουςχώρους Φρεσέτ ο ένα έχει ακόμα πλήρης μετρική ,ενώ οι LF-χώροι είναι πλήρεις ομοιόμορφοι διανυσματικοί χώροι που εγείρονται σαν όρια των χώρων Φρεσέτ.
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
Πηγές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Bourbaki 1987, V.86
- ↑ see Theorem 1.3.9, p. 20 in Megginson (1998).
- ↑ see Corollary 1.4.18, p. 32 in Megginson (1998).
- ↑ see Banach (1932), p. 182.
- ↑ see pp. 17–19 in Carothers (2005).
- ↑ see Banach (1932), pp. 11-12.
- ↑ see Banach (1932), Th. 9 p. 185.
- ↑ see Theorem 6.1, p. 55 in Carothers (2005)
- ↑ Several books about functional analysis use the notation X ∗ for the continuous dual, for example Carothers (2005), Lindenstrauss & Tzafriri (1977), Megginson (1998), Ryan (2002), Wojtaszczyk (1991).
- ↑ Theorem 1.9.6, p. 75 in Megginson (1998)
- ↑ see also Theorem 2.2.26, p. 179 in Megginson (1998)
- ↑ see p. 19 in Carothers (2005).
- ↑ Theorems 1.10.16, 1.10.17 pp.94–95 in Megginson (1998)
- ↑ Theorem 1.12.11, p. 112 in Megginson (1998)
- ↑ Theorem 2.5.16, p. 216 in Megginson (1998).
- ↑ see II.
- ↑ 17,0 17,1 17,2 see Theorem 2.6.23, p. 231 in Megginson (1998).
- ↑ see N. Bourbaki, (2004), "Integration I", Springer Verlag, ISBN 3-540-41129-1.
- ↑ 19,0 19,1 Eilenberg, Samuel (Jan 22, 1942). «Banach Space Methods in Topology». Annals of Mathematics 43 (3): 568. doi:.
- ↑ see also Banach (1932), p. 170 for metrizable K and L.
- ↑ see D. Amir, "On isomorphisms of continuous function spaces".
- ↑ M. Cambern, "A generalized Banach-Stone theorem".
- ↑ H. B. Cohen, "A bound-two isomorphism between C(X) Banach spaces".
- ↑ see for example W. Arveson, (1976), "An Invitation to C*-Algebra", Springer-Verlag, ISBN 0-387-90176-0.
- ↑ R. C. James (1951). «A non-reflexive Banach space isometric with its second conjugate space». Proc. Natl. Acad. Sci. U.S.A. 37: 174–177. doi:.
- ↑ see Lindenstrauss & Tzafriri (1977), p. 25.
- ↑ see E. Bishop and R. Phelps, "A proof that every Banach space is subreflexive".
- ↑ see III.
- ↑ see Corollary 2, p. 11 in Diestel (1984).
- ↑ see p. 85 in Diestel (1984).
- ↑ Rosenthal, Haskell P. (1974), "A characterization of Banach spaces containing ℓ1", Proc.
- ↑ see p. 201 in Diestel (1984).
- ↑ Odell, Edward W.; Rosenthal, Haskell P. (1975), «A double-dual characterization of separable Banach spaces containing ℓ1», Israel J. Math. 20: 375–384, doi:.
- ↑ Odell and Rosenthal, Sublemma p. 378 and Remark p. 379.
- ↑ for more on pointwise compact subsets of the Baire class, see Bourgain, Jean; Fremlin, D. H.; Talagrand, Michel (1978), «Pointwise Compact Sets of Baire-Measurable Functions», Am. J. Math. 100: 845–886, doi:.
- ↑ see Proposition 2.5.14, p. 215 in Megginson (1998).
- ↑ see for example p. 49, II.
- ↑ see Corollary 2.8.9, p. 251 in Megginson (1998).
- ↑ see Lindenstrauss & Tzafriri (1977) p. 3.
- ↑ the question appears p. 238, §3 in Banach's book, Banach (1932).
- ↑ see S. V. Bočkarev, "Existence of a basis in the space of functions analytic in the disc, and some properties of Franklin's system".
- ↑ see P. Enflo, "A counterexample to the approximation property in Banach spaces".
- ↑ see R.C. James, "Bases and reflexivity of Banach spaces".
- ↑ see A. Grothendieck, "Produits tensoriels topologiques et espaces nucléaires".
- ↑ see chap. 2, p. 15 in Ryan (2002).
- ↑ see chap. 3, p. 45 in Ryan (2002).
- ↑ see Example. 2.19, p. 29, and pp. 49–50 in Ryan (2002).
- ↑ see Proposition 4.6, p. 74 in Ryan (2002).
- ↑ see Pisier, Gilles (1983), "Counterexamples to a conjecture of Grothendieck", Acta Math. 151:181–208.
- ↑ see Szankowski, Andrzej (1981), "B(H) does not have the approximation property", Acta Math. 147: 89–108.
- ↑ see Kwapień, S. (1970), "A linear topological characterization of inner-product spaces", Studia Math. 38:277–278.
- ↑ see Lindenstrauss, J. and Tzafriri, L. (1971), "On the complemented subspaces problem", Israel J. Math. 9:263–269.
- ↑ see p. 245 in Banach (1932).
- ↑ 54,0 54,1 Gowers, W. T. (1996), "A new dichotomy for Banach spaces", Geom.
- ↑ see Gowers, W. T. (1994), "A solution to Banach's hyperplane problem", Bull.
- ↑ see Komorowski, Ryszard A. and Tomczak–Jaegermann, Nicole (1995), "Banach spaces without local unconditional structure", Israel J. Math. 89:205–226 and also (1998), "Erratum to: Banach spaces without local unconditional structure", Israel J. Math. 105:85–92.
- ↑ Milyutin, Alekseĭ A. (1966), "Isomorphism of the spaces of continuous functions over compact sets of the cardinality of the continuum".
- ↑ Milutin.
- ↑ One can take α = ω βn, where β + 1 is the Cantor–Bendixson rank of K, and n > 0 is the finite number of points in the β-th derived set K(β) of K. See Mazurkiewicz, Stefan; Sierpiński, Wacław (1920), "Contribution à la topologie des ensembles dénombrables", Fundamenta Mathematicae 1: 17–27.
- ↑ Bessaga, Czesław; Pełczyński, Aleksander (1960), "Spaces of continuous functions.
|




























![{\displaystyle {\begin{aligned}C(K){\widehat {\otimes }}_{\varepsilon }Y&\simeq C(K,Y),\\L^{1}([0,1]){\widehat {\otimes }}_{\pi }Y&\simeq L^{1}([0,1],Y),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdda0e4532c785e0ccddd2743db91e009ace27bb)




























![{\displaystyle \|f\|=\sum _{i=0}^{n}\sup \nolimits _{x\in [a,b]}\left|f^{(i)}(x)\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1a1a53ee5f74ba1c00ded97c44862d0bf691501)