Χρήστης:Efitpl/πρόχειρο
 |
Αυτή η σελίδα είναι το κύριο «πρόχειρο χρήστη» του Efitpl. Ένα «πρόχειρο χρήστη» είναι υποσελίδα της προσωπικής σελίδας του χρήστη στη Βικιπαίδεια. Εξυπηρετεί ως χώρος πειραματισμών και ανάπτυξης σελίδων και δεν είναι εγκυκλοπαιδικό λήμμα. Επεξεργαστείτε ή δημιουργήστε το δικό σας πρόχειρο εδώ ή κάνετε δοκιμές στο κοινόχρηστο Πρόχειρο Βικιπαίδειας. |
{{Σειρές Φουριέ}}
Στα μαθηματικά, μια σειρά Φουριέ (αγγλική προφορά : /'fɔərieɪ/) είναι ένας τρόπος περιγραφής ενός κύματος που λειτουργεί ως ένας συνδυασμός απλών ημιτονοειδών κυμάτων. Πιο τυπικά, αποσυνθέτει κάθε περιοδική συνάρτηση ή περιοδικό σήμα στο άθροισμα (ενδεχομένως άπειρο) ενός συνόλου απλών συναρτήσεων ταλάντωσης, δηλαδή ημιτόνων και συνημιτόνων (ή σύνθεση εκθετικών). Ο Διακριτού χρόνου Μετασχηματισμός Φουριέ είναι μια περιοδική συνάρτηση, που συχνά ορίζεται με όρους μιας σειράς Φουριέ. Επίσης ο Ζ-μετασχηματισμός μετατρέπεται σε μια σειρά Φουριέ με σημαντική προυπόθεση οτι | z | = 1.Οι Σειρές Φουριέ είναι κεντρικής σημασίας για την πρωτότυπη απόδειξη του Nyquist-Shannon θεώρημα δειγματοληψίας. Η μελέτη των Σειρών Φουριέ είναι ένας κλάδος της Ανάλυσης Φουριέ.
|
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Οι σειρές Φουριέ ονομάστηκαν προς τιμήν του Jean-Baptiste Joseph Fourier (1768-1830), ο οποίος έκανε σημαντικές συμβολές στη μελέτη των τριγωνομετρικών σειρών, μετά από προκαταρκτικές έρευνες των Leonhard Euler, Jean le Rond d'Alembert και Daniel Bernoulli.[nb 1] Ο Φουριέ εισήγαγε τη σειρά Fourier για το σκοπό της επίλυσης της εξίσωσης θερμότητας σε μια μεταλλική πλάκα, δημοσιεύοντας τα πρώτα αποτελέσματα του στο έργο του 1807 Mémoire sur la propagation de la chaleur dans les corps solides ( Πραγματεία για τη διάδοση της θερμότητας σε στερεά σώματα), και τη Théorie analytique de la chaleur το 1822. Οι πρώτες ιδέες για την αποσύνθεση μιας περιοδικής συνάρτησης σε άθροισμα απλών συναρτήσεων ταλάντωσης χρονολογούνται από τον 3ο αιώνα π.Χ., όταν οι αρχαίοι αστρονόμοι πρότειναν ένα εμπειρικό μοντέλο των πλανητικών κινήσεων, βασισμένο στην κυκλική τροχιά.
Η εξίσωση θερμότητας είναι μία μερική διαφορική εξίσωση. Πριν από τη δουλειά του Φουριέ, καμία λύση για την εξίσωση της θερμότητας δεν ήταν γνωστή στη γενική περίπτωση, αν και ήταν γνωστές μερικές λύσεις, όταν η πηγή θερμότητας συμπεριφερόταν με έναν απλό τρόπο, ειδικότερα, εάν η πηγή θερμότητας ήταν ημιτονοειδές ή συνημιτονοειδές κύμα. Αυτές οι απλές λύσεις μερικές φορές ονομάζονται ιδιοτιμές και ιδιοδιανύσματα. Ιδέα του Φουριέ ήταν να διαμορφώσει μία περίπλοκη πηγή θερμότητας ως μια υπέρθεση (ή γραμμικό συνδυασμό) των απλών ημιτονοειδών και συνημιτονοειδών κυμάτων, και να γράψει τη λύση ως υπέρθεση των ιδιοδιανυσμάτων και ιδιοτιμών. Αυτή η υπέρθεση ή γραμμικός συνδυασμός ονομάζεται σειρά Φουριέ.
Από μια σύγχρονη άποψη, τα αποτελέσματα του Fourier είναι κάπως άτυπα, λόγω έλλειψης της ακριβούς έννοιας της συνάρτησης και του ολοκληρώματος στις αρχές του δέκατου ένατου αιώνα. Αργότερα, οι Peter Gustav Lejeune Dirichlet[1] και Bernhard Riemann[2][3][4] εξέφρασαν τα αποτελέσματα του Φουριέ με μεγαλύτερη ακρίβεια και τυπικότητα.
Αν και το αρχικό κίνητρο ήταν η επίλυση της εξίσωσης θερμότητας, αργότερα έγινε φανερό ότι οι ίδιες τεχνικές μπορούν να εφαρμοστούν σε ένα ευρύ φάσμα των μαθηματικών και φυσικών προβλημάτων, και ιδιαίτερα εκείνες που αφορούν γραμμικές διαφορικές εξισώσεις με σταθερούς συντελεστές, για τις οποίες οι ιδιοτιμές και τα ιδιοδιανύσματα έχουν ημιτονοειδή μορφή. Οι Σειρές Φουριέ έχουν πολλές τέτοιες εφαρμογές σε ηλεκτρική εφαρμοσμένη μηχανική, ανάλυση κραδασμών, ακουστική, οπτική, επεξεργασία σήματος, επεξεργασία εικόνας, κβαντική μηχανική, οικονομετρία[5],θεωρία λεπτού κέλυφους με τοιχώματα[6] κλπ.
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Σε αυτή την ενότητα, s(x) είναι μια συναστηση της πραγματικής μεταβλητής x, και η s είναι ολοκληρώσιμη στο διάστημα [x 0 , x 0 + P], για τους πραγματικούς αριθμούς x 0 και P. Εμείς θα προσπαθήσουμε να αναπαραστήσουμε το s σε αυτό το διάστημα ως ένα άπειρο άθροισμα, ή Σειρά, από αρμονικές συναρτήσεις. Έξω από το διάστημα, η σειρά είναι περιοδική με περίοδο P (συχνότητα 1 /P). Επομένως, αν η s διαθέτει επίσης αυτή την ιδιότητα, η προσέγγιση ισχύει σε ολόκληρη την πραγματική ευθεία. Μπορούμε να ξεκινήσουμε με ένα πεπερασμένο άθροισμα (ή μερικό άθροισμα) :
είναι μια περιοδική συνάρτηση με περίοδο Ρ. Χρησιμοποιώντας τις ταυτότητες :

μπορούμε επίσης να γράψουμε τη συνάρτηση σε αυτές τις ισοδύναμες μορφές:
όπου:
Όταν οι συντελεστές (γνωστοί ως συντελεστές Φουριέ) υπολογίζονται ως εξής :[7]
προσεγγίζει την στο διάστημα και η προσέγγιση βελτιώνεται καθώς N → ∞.Το άθροισμα άπειρων όρων, ονομάζεται σειρά Φουριέ που αναπαριστά το Στην εφαρμοσμένη μηχανική, η σειρά Φουριέ γενικά θεωρείται ότι συγκλίνει παντού εκτός από τα σημεία ασυνέχειας, δεδομένου ότι οι συναρτήσεις που συναντώνται στη μηχανική είναι πιο καλά ορισμένες από αυτές που οι μαθηματικοί μπορούν να παρέχουν ως αντι-παραδείγματα σε αυτό το τεκμήριο. Ειδικότερα, η σειρά Φουριέ συγκλίνει απόλυτα και ομοιόμορφα στο s(x) όταν η παράγωγος του s(x) (η οποία δεν μπορεί να υπάρχει παντού) είναι τετράγωνο.[8] Αν μια συνάρτηση είναι τετράγωνο-ολοκληρώσιμη στο διάστημα [x 0 , x 0 + P], τότε η σειρά Φουριέ συγκλίνει προς τη συνάρτηση σχεδόν σε κάθε σημείο. Δείτε Σύγκλιση της σειράς Φουριέ. Είναι δυνατόν να καθοριστούν οι συντελεστές Φουριέ για γενικότερες συναρτήσεις ή κατανομές, σε τέτοιες περιπτώσεις, η σύγκλιση στο πρότυπο ή ασθενής σύγκλιση είναι συνήθως ενδιαφέρον.
-
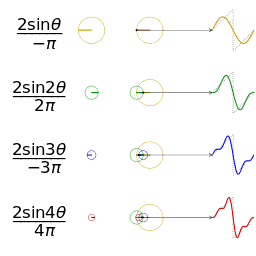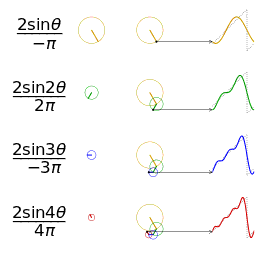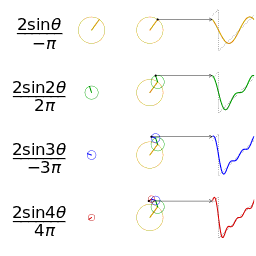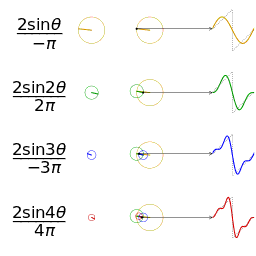
Μια άλλη απεικόνιση της προσέγγισης του ενός τετραγωνικού κύματος με τη λήψη των πρώτων 1, 2, 3 και 4 όρους της σειράς Fourier
-
Μια απεικόνιση μιας προσέγγισης ενός πριονωτού κύματος του ίδιου πλάτους και συχνότητας για σύγκριση
Παράδειγμα 1: μια απλή σειρά Fourier[Επεξεργασία | επεξεργασία κώδικα]


Χρησιμοποιούμε τον παραπάνω τύπο για να επεκτείνουμε μια σειρά Φουριέ μιας πολύ απλής συνάρτησης. Σκεφτείτε ένα πριονωτό κύμα
Στην περίπτωση αυτή, οι συντελεστές Φουριέ δίνονται από
Μπορεί να αποδειχθεί ότι η σειρά Φουριέ συγκλίνει s(x) σε κάθε σημείο x, όπου s είναι διαφορίσιμη, και ως εκ τούτου:
-
()
Όταν x =π,η σειρά Φουριέ συγκλίνει στο 0, που είναι το μισό άθροισμα από το αριστερό και το δεξί όριο της s στο x = π.Αυτή είναι μια ιδιαίτερη περίπτωση του θεωρήματος Dirichlet για τη σειρά Φουριέ.

Αυτό το παράδειγμα μας οδηγεί σε μια λύση του προβλήματος Basel
Παράδειγμα 2: τα κίνητρα του Φουριέ[Επεξεργασία | επεξεργασία κώδικα]
Η επέκταση της σειράς Fourier στη συνάρτησή μας στο παράδειγμα 1 φαίνεται λιγότερο απλή από ό, τι ο τύπος s(x) = x / π, και γι 'αυτό δεν είναι άμεσα εμφανής γιατί χρειάζεται κανείς αυτή τη σειρά Φουριέ. Ενώ υπάρχουν πολλές εφαρμογές, αναφέρουμε το κίνητρο του Φουριέ για την επίλυση της εξίσωσης της θερμότητας. Για παράδειγμα, θεωρήστε μια μεταλλική πλάκα σε σχήμα τετραγώνου με μήκος πλευράς π μέτρα, με συντεταγμένες (x, y) ∈ [0, π] × [0, π]. Αν δεν υπάρχει πηγή θερμότητας εντός της πλάκας, και αν τρεις από τις τέσσερις πλευρές διατηρούνται στους 0 βαθμούς Κελσίου, ενώ η τέταρτη πλευρά, που δίνεται από y = π, διατηρείται στη βαθμίδα θερμοκρασίας T(x, π) = x βαθμούς Κελσίου, για x στο (0, π), τότε μπορεί κανείς να δείξει ότι η στάσιμη κατανομή της θερμότητας (ή η κατανομή της θερμότητας μετά από μια μακρά χρονική περίοδο έχει παρέλθει) δίνεται από
Εδώ, sinh είναι η υπερβολική ημιτονοειδής συνάρτηση. Η λύση της εξίσωσης θερμότητας προκύπτει από τον πολλαπλασιασμό κάθε όρου του Eq.1 με sinh (ny) / sinh(nπ). Ενώ η συνάρτηση μας s(x) στο παράδειγμα , φαίνεται να έχει μια άσκοπα περίπλοκη σειρά Φουριέ, η κατανομή της θερμότητας T(x, y) είναι τετριμμένη.Η συνάρτηση Τ δεν μπορεί να γραφτεί ως έκφραση κλειστής μορφής. Αυτή η μέθοδος για την επίλυση του προβλήματος της θερμότητας κατέστη δυνατή από την εργασία του Φουριέ.
Άλλες εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]
Μία άλλη εφαρμογή αυτής της σειράς Φουριέ είναι η επίλυση του προβλήματος Basel με τη χρήση του θεωρήματος του Parseval. Το παράδειγμα γενικεύεται και μπορεί κανείς να υπολογίσει ζ (2n), για κάθε θετικό ακέραιο n.
Άλλα κοινά σύμβολα[Επεξεργασία | επεξεργασία κώδικα]
O συμβολισμός cn είναι ανεπαρκής για να συζητηθούν οι συντελεστές Φουριέ διαφόρων συναρτήσεων. Ως εκ τούτου, συνήθως αντικαθίσταται από μια τροποποιημένη μορφή της συνάρτησης (s, σε αυτήν την περίπτωση), όπως ή S και ο συμβολισμός της συνάρτησης αντικαθιστά συχνά τον παρακάτω τύπο:
Στη μηχανική, ιδιαίτερα όταν η μεταβλητή x παριστάνει χρόνο, ο συντελεστής της σειράς ονομάζεται πεδίο συχνότητας αναπαράστασης. Οι αγκύλες χρησιμοποιούνται συχνά για να τονίσουν ότι το πεδίο αυτής της συνάρτησης είναι ένα διακριτό σύνολο των συχνοτήτων.
Μια άλλη κοινή αναπαράσταση του πεδίου συχνοτήτων χρησιμοποιεί τους συντελεστές της σειράς Fourier για την διαμόρφωση της χτένας Dirac:
όπου το f παριστάνει ένα συνεχές πεδίο της συχνότητας. Όταν η μεταβλητή x έχει μονάδες δευτερολέπτων,το f έχει μονάδες hertz. Τα «δόντια» της χτένας απέχουν κατά πολλαπλάσια (δηλ. αρμονικές) του 1/Ρ, το οποίο ονομάζεται θεμελιώδης συχνότητα.Το μπορεί να αντικατασταθεί από την αναπαράσταση του αντίστροφου μετασχηματισμού Φουριέ:
Η συνάρτηση S(f) που κατασκευάσαμε αναφέρεται συνήθως ως μετασχηματισμός Φουριέ έστω και αν το ολοκλήρωμα Φουριέ της περιοδικής συνάρτησης δεν συγκλίνει στις αρμονικές συχνότητες.[nb 2]
Επεκτάσεις[Επεξεργασία | επεξεργασία κώδικα]
Σειρές Φουριέ στο τετράγωνο[Επεξεργασία | επεξεργασία κώδικα]
Μπορούμε επίσης να ορίσουμε τις σειρές Φουριέ για συναρτήσεις με δύο μεταβλητές x και y στο τετράγωνο [−π, π]×[−π, π]:
Εκτός από το να είναι χρήσιμες για την επίλυση μερικών διαφορικών εξισώσεων, όπως η εξίσωση της θερμότητας, μια αξιοσημείωτη εφαρμογή των σειρών Φουριέ στο τετράγωνο είναι η συμπίεση εικόνας. Συγκεκριμένα, το πρότυπο συμπίεσης εικόνας jpeg χρησιμοποιεί το δισδιάστατο διακριτό μετασχηματισμό συνημιτόνου, που είναι ένας μετασχηματισμός Φουριέ που χρησιμοποιεί τις βασικές συνημιτονοειδείς συναρτήσεις.
Σειρές Φουριέ σε Bravais-πλέγμα-περιοδικών-συναρτήσεων[Επεξεργασία | επεξεργασία κώδικα]
Το πλέγμα Bravais ορίζεται ως το σύνολο των διανυσμάτων της μορφής:
όπου ni είναι ακέραιοι και ai είναι τρία γραμμικά ανεξάρτητα διανύσματα. Υποθέτοντας ότι έχουμε κάποια συνάρτηση,f(r), έτσι ώστε να ικανοποιεί την παρακάτω συνθήκη για οποιοδήποτε διάνυσμα πλέγματος Bravais R:f(r) =f(r+R), θα μπορούσαμε να φτιάξουμε μια σειρά Φουριέ. Αυτό το είδος της συνάρτησης μπορεί να είναι, για παράδειγμα, το ενεργό δυναμικό που ένα ηλεκτρόνιο "αισθάνεται" μέσα σε ένα περιοδικό κρύσταλλο. Είναι χρήσιμο να φτιάχνουμε μια σειρά Φουριέ του δυναμικού αφού έχουμε εφαρμόσει το θεώρημα του Bloch. Αρχικά, μπορούμε να γράψουμε οποιοδήποτε αυθαίρετο διάνυσμα r στο σύστημα συντεταγμένων του πλέγματος:
όπου ai = |ai|. Έτσι μπορούμε να ορίσουμε μια νέα συνάρτηση,
Αυτή η νέα συνάρτηση, , είναι τώρα μια συνάρτηση τριών μεταβλητών καθεμία από τις οποίες έχει περιοδικότητα a1, a2, a3 αντίστοιχα : . Αν γράψουμε μια σειρά του g στο διάστημα [0, a1] για x1, μπορούμε να ορίσουμε το εξής :
Και μετά μπορούμε να γράψουμε:
Ορίζοντας έτσι:
Μπορούμε να γράψουμε το g ακόμη μια φορά ως :
Τελικά εφαρμόζοντας το ίδιο για την τρίτη συντεταγμένη, ορίζουμε :
Γράφουμε το g ως :
Αναδιοργανώνουμε:
Τώρα κάθε ανάστροφο πλέγμα διανυσμάτων μπορεί να γραφεί ως , όπου li είναι ακέραιοι και gi είναι το ανάστροφο πλέγμα διανυσμάτων, μπορούμε να χρησιμοποιήσουμε το γεγονός ότι για να υπολογίσουμε ότι για κάθε αυθαίρετο ανάστροφο πλέγμα διανυσμάτων Κ και αυθαίρετο διάνυσμα στο χώρο r, το αριθμητικό τους γινόμενο είναι:
Είναι λοιπόν ξεκάθαρο ότι στη δική μας επέκταση, το άθροισμα εξαρτάται στην πραγματικότητα από το ανάστροφο πλέγμα διανυσμάτων :
όπου
Υποθέτοντας
μπορούμε να λύσουμε αυτό το σύστημα των τριών γραμμικών εξισώσεων ως προς x,y, και z συναρτήσει των x1, x2 και x3 προκειμένου να υπολογίσουμε το στοιχείο του όγκου σε ένα αρχέτυπο καρτεσιανό σύστημα συντεταγμένων. Μόλις έχουμε x,y, και z συναρτήσει των x1, x2 και x3, μπορούμε να υπολογίσουμε την Ιακωβιανή ορίζουσα:
η οποία μετά από υπολογισμούς και εφαρμόζοντας μη τετριμμένες ταυτότητες εξωτερικού γινομένου μπορεί να αποδειχθεί ότι είναι ίση με :
(μπορεί να είναι επωφελής για χάρη της απλούστευσης των υπολογισμών, να εργαζόμαστε σε ένα τέτοιο καρτεσιανό σύστημα συντεταγμένων, στο οποίο τυχαίνει το a1 να είναι παράλληλο στον άξονα των x, το a2 να ανήκει στο έπίπεδο x-y , και το a3 να έχει τις συνιστώσες του και στους τρείς άξονες). Ο παρονομαστής είναι ακριβώς ο όγκος της αρχικής μοναδιαίας σφαίρας που περικλείεται από τα τρία αρχικά-διανύσματα a1, a2 και a3. Πιο συγκεκριμένα, γνωρίζουμε πλέον ότι
Μπορούμε να γράψουμε τώρα h(Κ) ως ολοκλήρωμα με το παραδοσιακό σύστημα συντεταγμένων του όγκου της αρχικής σφαίρας, αντί με τις x1, x2 και x3 μεταβλητές :
Και το C είναι η αρχική μονάδα της σφαίρας, έτσι, είναι ο όγκος της αρχικής μοναδιαίας σφαίρας.
Ερμηνεία χώρου Hilbert[Επεξεργασία | επεξεργασία κώδικα]
Στη γλώσσα τoy χώρου Hilbert, το σύνολο των συναρτήσεων {; n ∈ Z} είναι mia ορθοκανονική βάση για στο χώρο L2([−π, π]) των τετραγωνικά ολοκληρώσιμων συναρτήσεων στο [−π, π]. Αυτός ο χώρος είναι στην πραγματικότητα ένας χώρος Hilbert με εσωτερικό γινόμενο που δίνεται για δύο οποιαδήποτε στοιχεία f και g από τον τύπο : Οι βασικές σειρές Φουριέ που δίνουν αποτελέσματα για τους χώρους Hilbert μπορούν να γραφούν ως

Αυτό αντιστοιχεί ακριβώς στη μιγαδική εκθετική προσέγγιση που δίδεται παραπάνω. Η εκδοχή με τα ημίτονα και τα συνημίτονα αποδεικνύεται επίσης με την ερμηνεία του χώρου Hilbert. Πράγματι, τα ημίτονα και τα συνημίτονα αποτελούν ένα ορθοκανονικό σύνολο:
(όπου δmn είναι το Δέλτα του Κρόνεκερ), και
επιπλέον τα ημίτονα και τα συνημίτονα είναι ορθογώνια στη συνεχή συνάρτηση 1. Μια ορθοκανονική βάση στον L2([−π, π]) αποτελείται από πραγματικές συναρτήσεις που σχηματίζονται από τις συναρτήσεις 1/√2π 1 και 1/√π cos(nx), 1/√π sin(nx) με n = 1, 2,... . Η πυκνότητα του αναπτύγματός τους (span) είναι συνέχεια του θεωρήματος Stone-Weierstrass, αλλά προκύπτει και από τις ιδιότητες των κλασικών πυρήνων, όπως οι πυρήνες Fejér.
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Λέμε ότι η f ανήκει στο αν η f είναι 2π-περιοδική συνάρτηση στον R που είναι k φορές παραγωγίσιμη και η κ-στη παράγωγος είναι συνεχής.
- Αν η f είναι μια 2π-περιοδική περιττή συνάρτηση, τότε, an = 0 για κάθε n.
- Αν η f είναι μια 2π-περιοδική άρτια συνάρτηση, τότε, bn = 0 για κάθε n.
- Αν η f είναι ολοκληρώσιμη, , και .Το αποτέλεσμα αυτό είναι γνωστό ως λήμμα Riemann–Lebesgue
- Η διπλά άπειρη ακολουθία {an} στο c0(Z) είναι η ακολουθία των συντελεστών Φουριέ μιας συνάρτησης στον L1([0, 2π]) αν και μόνο αν είναι συνέλιξη δύο συναρτήσεων στον . Βλέπε
- Αν , τότε οι συντελεστές Φουριέ της παραγώγου f′ μπορούν να εκφραστούν συναρτήσει των συντελεστών Φουριέ της συνάρτησης f, μέσω του τύπου .
- Αν , τότε . Πιο συγκεκριμένα, όταν η τείνει στο μηδέν, προκύπτει ότι το τείνει στο μηδέν, το οποίο σημαίνει ότι οι συντελεστές Φουριέ συγκλίνουν στο μηδέν πιο γρήγορα από την k-στη δύναμη του n.
- Το θεώρημα του Parseval. Αν η f ανήκει στον L2([−π, π]), τότε .
- Το θεώρημα του Plancherel. Αν είναι συντελεστές και τότε υπάρχει μια μοναδική συνάρτηση τέτοια ώστε για κάθε n.
- Το πρώτο θεώρημα συνέλιξης υποστηρίζει ότι αν η f και η g ανήκουν στον L1([−π, π]), οι συντελεστές των σειρών Φουριέ της 2π-περιοδικής συνέλιξης των f και g δίνονται από τον τύπο :
- όπου:
- Το δεύτερο θεώρημα συνέλιξης αναφέρει ότι οι συντελεστές των σειρών Φουριέ του γινομένου της f και g δίνεται από την διακριτή συνέλιξη των και ακολουθιών :
Προσέγγιση και σύγκλιση των σειρών Φουριέ[Επεξεργασία | επεξεργασία κώδικα]
Ένα σημαντικό ζήτημα τόσο για τη θεωρία όσο και τις εφαρμογές είναι αυτό της σύγκλισης. Ειδικότερα, είναι συχνά απαραίτητο σε εφαρμογές για να αντικαταστήσουμε την άπειρη σειρά με μια πεπερασμένη,
Αυτό καλείται μερικό άθροισμα . Θα θέλαμε να γνωρίζουμε, με ποια έννοια η fN(x) συγκλίνει στην f(x) καθώς N → ∞.
Ιδιότητες ελαχίστων τετραγώνων[Επεξεργασία | επεξεργασία κώδικα]
Λέμε ότι p είναι ένα τριγωνομετρικό πολυώνυμο βαθμού Ν όταν είναι της μορφής : Να σημειώσουμε ότι η fN είναι τριγωνομετρικό πολυώνυμο βαθμού N. Από το θεώρημα του Parseval συνεπάγεται ότι
Θεώρημα. Το τριγωνομετρικό πολυώνυμο fN είναι το μοναδικό βέλτιστο τριγωνομετρικό πολυώνυμο βαθμού N που προσεγγίζει την f(x), με την έννοια ότι, για οποιοδήποτε τριγωνομετρικό πολυώνυμο p ≠ fN βαθμού Ν, έχουμε
όπου η νόρμα του χώρου Hilbert ορίζεται ως :
Σύγκλιση[Επεξεργασία | επεξεργασία κώδικα]
Λόγω της σημαντικότας της μεθόδου των ελαχίστων τετραγώνων, και λόγω της πληρότητας της βάσης της σειράς Φουριέ, έχουμε αποκτήσει ένα στοιχειώδες αποτέλεσμα σύγκλισης.
Θεώρημα. Αν η f ανήκει στο L2([−π, π]), τότε f∞ συγκλίνει στο f στο L2([−π, π]), που σημαίνει ότι , συγκλίνει στο 0 καθώς N → ∞. Έχουμε ήδη αναφέρει ότι αν η f είναι συνεχής διαφορίσιμη συνάρτηση, τότε είναι ο n-οστος συντελεστής της σειράς Φουριέ της παραγώγου f′. Επομένως, συνεπάγεται κατ 'ουσίαν, από την ανισότητα Cauchy-Schwarz, όπου f∞ είναι απολύτως αθροίσιμη.Το άθροισμα αυτής της σειράς είναι μία συνεχής συνάρτηση, ίση με f, δεδομένου ότι η σειρά Φουριέ συγκλίνει κατά μέση τιμή στην f.
Θεώρημα. Αν , τότε η f∞ συγκλίνει στην f ομοιόμορφα (και, ως εκ τούτου, επίσης, σημειακά.) Το συμπέρασμα αυτό μπορεί να αποδειχθεί εύκολα, αν f επιπλέον θεωρείται ότι είναι C2, μιας και σε αυτήν την περίπτωση τείνει στο μηδέν καθώς n → ∞. Γενικότερα, η σειρά Φουριέ είναι απολύτως αθροίσιμη, έτσι συγκλίνει ομοιόμορφα στην f, υπό τον όρο ότι η f ικανοποιεί τη συνθήκη Hölder έτσι ώστε α > ½.Στην περίπτωση της απόλυτης άθροισης η ανισότητα αποδεικνύει την ομοιόμορφη σύγκλιση. Είναι γνωστά πολλά άλλα αποτελέσματα σχετικά με την σύγκλιση των σειρών Φουριέ,τα οποία κυμαίνονται από το απλό αποτέλεσμα ότι η σειρά συγκλίνει στο x αν f είναι διαφορίσιμη στο x, ως τα αποτελέσματα του Lennart Κάρλεσον που είναι πολύ πιο εξελιγμένα απο ότι η σειρά Φουριέ μιας L2 συνάρτησης που συγκλίνει σχεδόν παντού.
Αυτά τα θεωρήματα, και οι άτυπες παραλλαγές τους που δεν διευκρινίζουν τις προϋποθέσεις σύγκλισης, αναφέρονται αρκετές φορές ως «θεώρημα του Φουριέ» ή «το θεώρημα Φουριέ".[9][10][11][12]
Απόκλιση[Επεξεργασία | επεξεργασία κώδικα]
Μιας και οι σειρές Φουριέ έχουν τόσο καλές ιδιότητες σύγκλισης, πολλοί εκπλήσσονται συχνά από ορισμένα αρνητικά αποτελέσματα. Για παράδειγμα, η σειρά Φουριέ συνεχούς Τ-περιοδικής συνάρτησης δεν χρειάζεται να συγκλίνει κατά σημείο. Η αρχή ομοιόμορφου φράγματος αποδίδει μια απλή μη εποικοδομητική απόδειξη αυτού του γεγονότος. Το 1922, Andrey Kolmogorov δημοσίευσε ένα άρθρο με τίτλο "Une série de Fourier-Lebesgue divergente presque partout" στο οποίο έδωσε ένα παράδειγμα μιας Lebesgue-ολοκληρώσιμης συνάρτησης της οποίας η σειρά Φουριέ αποκλίνει σχεδόν παντού. Αργότερα, επίσης, κατασκευάστηκε ένα παράδειγμα ολοκληρώσιμης συνάρτησης της οποίας η σειρά Φουριέ αποκλίνει παντού (Katznelson 1976).
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Αυτοί οι τρεις έκαναν κάποια σημαντική εργασία για την εξίσωση του κύματος, ειδικά D'Alembert.Το έργο του Euler σε αυτόν τον τομέα ήταν ως επί το πλείστον η σύγχρονη/σε συνεργασία με Bernoulli, αν και ο τελευταίος έκανε κάποιες ανεξάρτητες συμβολές στη θεωρία των κυμάτων και των ταλαντώσεων (δείτε εδώ, pg.s 209 & 210).
- ↑ Αφού το ολοκλήρωμα που ορίζει ο μετασχηματισμός Fourier της περιοδικής συνάρτησης δε συγκλίνει, είναι απαραίτητο να εξετάσουμε την περιοδική συνάρτηση και την μετατροπή της, ως κατανομή. Με αυτή την έννοια είναι μια συνάρτηση δέλτα του Dirac, η οποία είναι ένα παράδειγμα κατανομής.
- ↑ Ο συντελεστής κλίμακας είναι πάντα ίσος με την περίοδο, 2π σε αυτή την περίπτωση <-.! Μπορεί εύκολα να διαπιστώσει κανείς ότι ο παράγοντας είναι απαραίτητος εδώ, επιλέγοντας στ και ζ να είναι σταθερά 1. -->
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Lejeune Dirichlet-, Π. " Sur la convergence des séries trigonométriques qui servent à une représenter fonction arbitraire entre des limites données ". (Στα γαλλικά), μετάφρ. «Με τη σύγκλιση των τριγωνομετρικών σειρών που χρησιμεύουν για να αντιπροσωπεύουν μια τυχαία συνάρτηση μεταξύ δύο καθορισμένων ορίων". Εφημερίδα f ¨ ur die reine und Angewandte Mathematik, Vol. 4 (1829), σσ. 157-169.
- ↑ «Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe» [About the representability of a function by a trigonometric series]. Habilitationschrift, Göttingen; 1854. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, vol. 13, 1867. Published posthumously for Riemann by Richard Dedekind (στα German). Αρχειοθετήθηκε από το πρωτότυπο στις 20 Μαΐου 2008. Ανακτήθηκε στις 19 Μαΐου 2008.
- ↑ D. Mascre, Bernhard Riemann: Posthumous Thesis on the Representation of Functions by Triginometric Series (1867). Landmark Writings in Western Mathematics 1640–1940, Ivor Grattan-Guinness (ed.); pg. 492. Elsevier, 20 May 2005.Accessed 7 Dec 2012.</
- ↑ Theory of Complex Functions: Readings in Mathematics, by Reinhold Remmert; pg 29. Springer, 1991. Accessed 7 Dec 2012.
- ↑ Nerlove, Marc· Grether, David M.· Carvalho, Jose L. (1995). Analysis of Economic Time Series. Economic Theory, Econometrics, and Mathematical Economics. Elsevier. ISBN 0-12-515751-7.
- ↑ Flugge, Wilhelm (1957). Statik und Dynamik der Schalen. Berlin: Springer-Verlag.
- ↑ Dorf, Richard C.· Tallarida, Ronald J. (15 Ιουλίου 1993). Pocket Book of Electrical Engineering Formulas (1 έκδοση). Boca Raton,FL: CRC Press. σελίδες 171–174. ISBN 0849344735.
- ↑ Georgi P. Tolstov (1976). Fourier Series. Courier-Dover. ISBN 0-486-63317-9.
- ↑ William McC. Siebert (1985). Circuits, signals, and systems. MIT Press. σελ. 402. ISBN 978-0-262-19229-3.
- ↑ L. Marton and Claire Marton (1990). Advances in Electronics and Electron Physics. Academic Press. σελ. 369. ISBN 978-0-12-014650-5.
- ↑ Hans Kuzmany (1998). Solid-state spectroscopy. Springer. σελ. 14. ISBN 978-3-540-63913-8.
- ↑ Karl H. Pribram, Kunio Yasue, and Mari Jibu (1991). Brain and perception. Lawrence Erlbaum Associates. σελ. 26. ISBN 978-0-89859-995-4.
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- William E. Boyce and Richard C. DiPrima (2005). Elementary Differential Equations and Boundary Value Problems (8th έκδοση). New Jersey: John Wiley & Sons, Inc. ISBN 0-471-43338-1.
- Joseph Fourier, translated by Alexander Freeman (published 1822, translated 1878, re-released 2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0. Ελέγξτε τις τιμές ημερομηνίας στο:
|year=(βοήθεια) 2003 unabridged republication of the 1878 English translation by Alexander Freeman of Fourier's work Théorie Analytique de la Chaleur, originally published in 1822. - Enrique A. Gonzalez-Velasco (1992). «Connections in Mathematical Analysis: The Case of Fourier Series». American Mathematical Monthly 99 (5): 427–441. doi:.
- Katznelson, Yitzhak (1976). An introduction to harmonic analysis (Second corrected έκδοση). New York: Dover Publications, Inc. ISBN 0-486-63331-4.
- Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
- Walter Rudin (1976). Principles of mathematical analysis (3rd έκδοση). New York: McGraw-Hill, Inc. ISBN 0-07-054235-X.
- A. Zygmund (2002). Trigonometric series (third έκδοση). Cambridge: Cambridge University Press. ISBN 0-521-89053-5. The first edition was published in 1935.












![{\displaystyle \scriptstyle [x_{0},\ x_{0}+P],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e15dd8a7d5176a8625325e2afb151fbdd825a142)


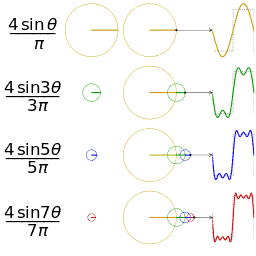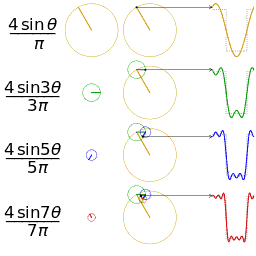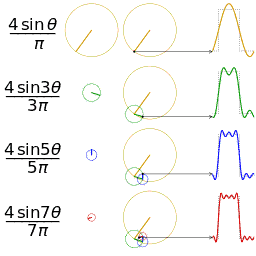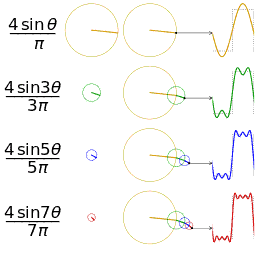



![{\displaystyle {\begin{aligned}s(x)&={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]\\&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \mathrm {for} \quad x-\pi \notin 2\pi \mathbf {Z} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4f7723030e9a65dde2b59bdffde660c5ac6d1a4)


![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}(n)\cdot e^{i{\tfrac {2\pi nx}{P}}}\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{j{\tfrac {2\pi nx}{P}}}&&\scriptstyle {\text{common engineering notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1948743e8e50b99560a2e018c78b35e14e2111a1)
![{\displaystyle S(f)\ {\stackrel {\mathrm {def} }{=}}\ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/191fd9d4420479ce5300b692fbc43c0e5e703e89)

![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i{\tfrac {2\pi nx}{P}}}\ \ {\stackrel {\mathrm {def} }{=}}\ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f87bc7f858006ce49e2b5c40d429076b92b96df)









![{\displaystyle {\begin{aligned}h^{\mathrm {two} }(m_{1},m_{2},x_{3})&:={\frac {1}{a_{2}}}\int _{0}^{a_{2}}h^{\mathrm {one} }(m_{1},x_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{2}}{a_{2}}}x_{2}}\,dx_{2}\\[12pt]&={\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b375ad1bad97e4cee6cfa9c82d20582af5ba6b4)

![{\displaystyle {\begin{aligned}h^{\mathrm {three} }(m_{1},m_{2},m_{3})&:={\frac {1}{a_{3}}}\int _{0}^{a_{3}}h^{\mathrm {two} }(m_{1},m_{2},x_{3})\cdot e^{-i2\pi {\frac {m_{3}}{a_{3}}}x_{3}}\,dx_{3}\\[12pt]&={\frac {1}{a_{3}}}\int _{0}^{a_{3}}dx_{3}{\frac {1}{a_{2}}}\int _{0}^{a_{2}}dx_{2}{\frac {1}{a_{1}}}\int _{0}^{a_{1}}dx_{1}g(x_{1},x_{2},x_{3})\cdot e^{-i2\pi \left({\frac {m_{1}}{a_{1}}}x_{1}+{\frac {m_{2}}{a_{2}}}x_{2}+{\frac {m_{3}}{a_{3}}}x_{3}\right)}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bac3a4c30ff78f3abc70b6b65a6274b8899ca038)








![{\displaystyle {\begin{bmatrix}{\dfrac {\partial x_{1}}{\partial x}}&{\dfrac {\partial x_{1}}{\partial y}}&{\dfrac {\partial x_{1}}{\partial z}}\\[3pt]{\dfrac {\partial x_{2}}{\partial x}}&{\dfrac {\partial x_{2}}{\partial y}}&{\dfrac {\partial x_{2}}{\partial z}}\\[3pt]{\dfrac {\partial x_{3}}{\partial x}}&{\dfrac {\partial x_{3}}{\partial y}}&{\dfrac {\partial x_{3}}{\partial z}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5095a317a5c0975c5d1bdf27cd79d13b106a96a6)


























![{\displaystyle f\in L^{2}([-\pi ,\pi ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74d27747bf5e28fa54e94f218bd9296213ef25c5)

=2\pi \cdot {\hat {f}}(n)\cdot {\hat {g}}(n),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/956ea404aa998519c088c08c9a9e9f29c9bd38f0)
\ &{\stackrel {\mathrm {def} }{=}}\int _{-\pi }^{\pi }f(u)\cdot g[{\text{pv}}(x-u)]du,&&{\big (}{\text{and }}\underbrace {{\text{pv}}(x)\ {\stackrel {\mathrm {def} }{=}}{\text{Arg}}\left(e^{ix}\right)} _{\text{principal value}}{\big )}\\&=\int _{-\pi }^{\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when g(x) is 2}}\pi {\text{-periodic.}}\\&=\int _{2\pi }f(u)\cdot g(x-u)\,du,&&\scriptstyle {\text{when both functions are 2}}\pi {\text{-periodic, and the integral is over any 2}}\pi {\text{ interval.}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1223be49e9c8285ec78e1a81ac52e7f983702eeb)


=[{\hat {f}}*{\hat {g}}](n).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a01ca431cbe51c2353a325265bb70204e5a1ae1)









