Θεμελιώδης συχνότητα

Τρόποι ταλάντωσης και στάσιμα κύματα σε μια χορδή: η θεμελιώδης συχνότητα και οι εξι πρώτοι υπέρτονοι.

Η θεμελιώδης συχνότητα, που συχνά αναφέρεται απλώς ως το θεμελιώδες, ορίζεται ως η χαμηλότερη συχνότητα μιας περιοδικής κυματομορφής. Από τον ορισμό της, σε μια υπέρθεση των ημιτονοειδών (π.χ.σειρά Φουριέ), η θεμελιώδης συχνότητα είναι η χαμηλότερη ημιτονοειδής συχνότητα στο άθροισμα. Σε ορισμένα συμφραζόμενα, η θεμελιώδης γράφεται συντομευμένα συνήθως ως f0 (ή FF), υποδεικνύοντας τη χαμηλότερη συχνότητα μετρώντας από το μηδέν. Σε άλλες περιπτώσεις, είναι πιο σύνηθες να συντομεύεται ως f1, που αντιστοιχεί στην πρώτη αρμονική (η δεύτερη αρμονική είναι τότε f2 = f1 ⋅ 2, κλπ. Σε αυτό το πλαίσιο, η μηδενική αρμονική θα είναι στα 0 Hz.)

Επεξήγηση

Όλες οι ημιτονοειδείς και πολλές μη-ημιτονοειδείς κυματομορφές είναι περιοδικές, το οποίο σημαίνει επαναλαμβάνονται ακριβώς με την πάροδο του χρόνου. Η ενιαία περίοδος είναι επομένως η μικρότερη επαναλαμβανόμενη μονάδα ενός σήματος, και μία περίοδος περιγράφει το σήμα εντελώς. Μπορούμε να δείξουμε ότι μία κυματομορφή είναι περιοδική με την εύρεση της περιόδου Τ για την οποία η ακόλουθη εξίσωση ισχύει:

$x(t)=x(t+T){\text{ for all }}t\in \mathbb {R}$

Όπου χ (t) είναι η συνάρτηση της κυματομορφής.

Αυτό σημαίνει ότι για πολλαπλάσιες του κάποια περίοδο Τ η τιμή του σήματος είναι πάντα η ίδια. Η ελάχιστη δυνατή τιμή του Τ για την οποία αυτό είναι αλήθεια ονομάζεται θεμελιώδης περίοδος και η θεμελιώδης συχνότητα ("f"₀) είναι:

$f_{0}={\frac {1}{T}}$

Οταν f₀ είναι η θεμελιώδης συχνότητα και Τ είναι η θεμελιώδης περίοδος.

F0 κλειστό από αριστερά

F0 κλειστό από δεξιά

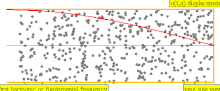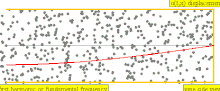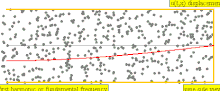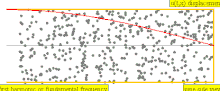
Για ένα σωλήνα μήκους L με το ένα άκρο κλειστό και το άλλο άκρο να ανοίγει το μήκος κύματος της θεμελιώδους αρμονικής είναι 4 L, όπως υποδεικνύεται από τις δυο πρώτες κινούμενες εικόνες στα δεξιά. ως εκ τούτου,

$\lambda _{0}=4L.$

Συνεπώς, χρησιμοποιώντας τη σχέση

$\lambda _{0}={\frac {v}{f_{0}}}$ ,

όπου ν είναι η ταχύτητα του κύματος, μπορούμε να βρούμε τη θεμελιώδη συχνότητα όσον αφορά την ταχύτητα του κύματος και το μήκος του σωλήνα:

$f_{0}={\frac {v}{4L}}.$

F0 και τα δυο κλειστά

F0 και τα δύο ανοιχτά

Εάν τα άκρα του ίδιου σωλήνα είναι πλέον κλειστά ή και τα δύο ανοιχτά ,όπως στις δύο κάτω κινούμενες εικόνες στα δεξιά, το μήκος κύματος της θεμελιώδους αρμονικής γίνεται 2L. Με την ίδια μέθοδο όπως παραπάνω, η θεμελιώδης συχνότητα έχει βρεθεί να είναι

$f_{0}={\frac {v}{2L}}.$

Στους 20 ° C (68 ° F) η ταχύτητα του ήχου στον αέρα είναι 343 m / s (1129 ft / s). Αυτή η ταχύτητα είναι εξαρτάται από τη θερμοκρασία και κάνει αύξηση με ρυθμό 0,6 m / s για κάθε βαθμό Κελσίου αύξηση της θερμοκρασίας (1,1 ft / s για κάθε αύξηση της 1 ° F).

Η ταχύτητα του ηχητικού κύματος σε διαφορετικές θερμοκρασίες: -

• v = 343,2 m / s στους 20 ° C
• v = 331,3 m / s στους 0 °C

Δείτε επίσης

• ιδιοσυχνότητα
• ταλάντωση
• Χερτζ
• Ηλεκτρονικός δέκτης
• Κλίμακα αρμονικών
• Αλγόριθμος ανίχνευσης Pitch