Μαγικό τετράγωνο

Το μαγικό τετράγωνο αποτελεί διάταξη αριθμών σε συστοιχία ίσου συνόλου γραμμών και στηλών, όπου η αριθμητική πράξη μεταξύ των αριθμών στην ίδια σειρά ή στήλη ή διαγώνιο του τετραγώνου επιστρέφει πάντα το ίδιο αποτέλεσμα.[1][2] Το κοινό αποτέλεσμα ονομάζεται μαγική σταθερά του μαγικού τετραγώνου. Η πλέον συνήθης αριθμητική πράξη στα μαγικά τετράγωνα είναι η πρόσθεση μεταξύ των αριθμών,[3][4]ενώ υπάρχουν και άλλες εκδοχές τους όπως η τέλεση αφαίρεσης ή πολλαπλασιασμού, καθώς και είναι δυνατό να αναπαρασταθούν σε τρισδιάστατη μορφή ως μαγικοί κύβοι, ή να υπάρξουν τροποποιήσεις όπου αντί για αριθμούς χρησιμοποιούνται σχήματα.
Η πρώτη περιγραφή μαγικού τετραγώνου υπήρξε στην Κίνα από την 3η χιλιετία π.Χ., κατόπιν μεταφέρθηκε στους Ινδούς κατά την ύστερη αρχαιότητα και μετέπειτα στους Άραβες, και από εκεί αργότερα στους Βυζαντινούς από όπου μεταδόθηκε στην υπόλοιπη Ευρώπη. Κατά τον Μεσαίωνα τα μαγικά τετράγωνα ήταν ιδιαίτερα δημοφιλή ως φυλακτά και αποτροπαϊκά σύμβολα. Στην σύγχρονη εποχή αποτελούν συχνό πεδίο ενασχόλησης των ψυχαγωγικών μαθηματικών και των μαθηματικών κλάδων της συνδυαστικής και στατιστικής, καθώς επίσης της τέχνης και του μυστικισμού, και επίσης σε ότι αφορά τις πρακτικές εφαρμογές τους χρησιμοποιούνται για τους σκοπούς της κρυπτογράφησης ψηφιακών εικόνων, ενώ στην μηχανική ρευστών για τον υπολογισμό κατακράτησης υδάτων σε επιφάνειες.
Βασικές ιδιότητες
[Επεξεργασία | επεξεργασία κώδικα]Μαγική σταθερά και κοινά αθροίσματα
[Επεξεργασία | επεξεργασία κώδικα]
Η μαγική σταθερά είναι το κοινό αποτέλεσμα που προκύπτει μετά την πρόσθεση των αριθμών σε κάθε γραμμή, στήλη, και διαγώνιο. Η σταθερά του κάθε τετραγώνου συμβολίζεται ως M και εξαρτάται από την τάξη του τετραγώνου (αριθμός κελιών σε γραμμή/στήλη, π.χ. για τετράγωνο διαστάσεων 3x3 τότε n=3), και υπολογίζεται από τον τύπο ,[1] καθώς το άθροισμα των είναι τα οποία όταν διαιρεθούν με το επιστρέφουν την μαγική σταθερά.
Διαφορετικό από την μαγική σταθερά, αλλά επίσης κοινό αποτέλεσμα μεταξύ των αριθμών του τετραγώνου μπορεί να προκύψει αν οι αριθμοί σε κάθε γραμμή λογιστούν ως ένας αριθμός, υψωθούν στο τετράγωνο, και προστεθούν. Το άθροισμα που προκύπτει ισούται με το άθροισμα των τετραγώνων (ως δύναμη) των αριθμών που προκύπτουν από την αντιμετάθεση των ψηφίων (ως παλίνδρομα) π.χ.:
- εάν το τετράγωνο αποτελείται από τους αριθμούς 1η σειρά: 6, 7, 2 | 2η: 1, 5, 9 | 3η: 8, 3, 4, τότε 672^2 + 159^2 + 834^2 = 276^2 + 951^2 + 438^2 = 1.172.421.[5]
- παράλληλα, προκύπτει επίσης κοινό άθροισμα από το άθροισμα των γινομένων των αριθμών στις γραμμές τα οποία ισούνται με το άθροισμα των γινομένων των αριθμών σε στήλες,[6] (6 x 7 x 2) + (1 x 5 x 9) + (8 x 3 x 4) = (6 x 1 x 8) + (7 x 5 x 3) + (2 x 9 x 4) = 225.
Αριθμητική πρόοδος
[Επεξεργασία | επεξεργασία κώδικα]Η αριθμητική πρόοδος είναι η διαφορά μεταξύ ενός αριθμού και του αμέσως επόμενου μεγαλύτερου αριθμού. Στα μαγικά τετράγωνα η πλέον κοινή πρόοδος είναι η αύξηση του αριθμού κατά 1 με τα μαγικά τετράγωνα να ονομάζονται κανονικά, όμως το ίδιο λειτουργική είναι και η αύξηση κατά 3, ή 5, ή οποιονδήποτε άλλο αριθμό, αθροιστικά ή ως γινόμενο ή με οποιοδήποτε άλλο τρόπο ώστε να επιτυγχάνεται ισορροπία μεταξύ των αριθμητικών τιμών των κελιών (π.χ. μέθοδος κατασκευής 3x3).[7][8]
Τάξεις
[Επεξεργασία | επεξεργασία κώδικα]Οι τρεις ομάδες τάξεων που μπορεί να ανήκει το κάθε μαγικό τετράγωνο είναι:[9]
- περιττής τάξης, όπου οι διαστάσεις του τετραγώνου βασίζονται σε περιττό αριθμό (1x1, 3x3, 5x5 κτλ). Αυτή είναι η συνηθέστερη περίπτωση.
- περιττής άρτιας τάξης, όπου οι διαστάσεις του τετραγώνου βασίζονται σε άρτιο αριθμό μη πολλαπλάσιο του 4 (2x2, 6x6, 10x10 κτλ) .
- αρτιάκις(D/R) άρτιας τάξης, όπου οι διαστάσεις του τετραγώνου βασίζονται σε άρτιο αριθμό πολλαπλάσιο του 4 (4x4, 8x8, 12x12 κτλ).
Κατανομή ανά τάξη
[Επεξεργασία | επεξεργασία κώδικα]Οι πιθανοί διαφορετικοί συνδυασμοί κελιών με αριθμούς που μπορεί να σχηματιστεί μαγικό τετράγωνο ανά τάξη n, εξαιρώντας την αναδιάταξη των ίδιων αριθμών στα κελιά (καθρέφτισμα και περιστροφή) και ανεξάρτητα από τον αριθμό εκκίνησης, είναι:[10][11]
- Το μαγικό τετράγωνο τάξεως 1 (διαστάσεις 1×1) διαθέτει μόνο έναν αριθμό, και ως εκ τούτου είναι ασήμαντο, ωστόσο εμπίπτει στον ορισμό μαγικού τετραγώνου όπου το άθροισμα των κελιών ενός πίνακα επιστρέφει το ίδιο άθροισμα πάντα.
- Δεν υπάρχουν μαγικά τετράγωνα διαστάσεων 2x2.[12]
- Υπάρχει μόνο ένα μαγικό τετράγωνο διαστάσεων 3x3.
- Υπάρχουν συνολικά 880 τετράγωνα διαστάσεων 4x4.
- Υπάρχουν 275.305.224 διαστάσεων 5x5.
- Για τα μαγικά τετράγωνα τάξεως 6 υπολογίζεται πως αυτά προσεγγίζουν τα 1,8 × 1019.
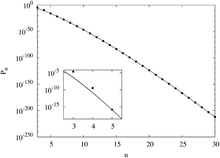
Η εκτίμηση του συνόλου των πιθανών μαγικών τετραγώνων σε μεγαλύτερες διαστάσεις είναι αρκετά δύσκολη, καθώς η στατιστική ανάλυση με χρήση της μεθόδου Μόντε Κάρλο[1] γίνεται με την τυχαία παραγωγή n × n πινάκων στοιχείων από το 1 έως το n2 και κατόπιν ελέγχεται αν το αποτέλεσμα είναι μαγικό τετράγωνο. Η πιθανότητα πως ένας τυχαία δημιουργημένος πίνακας αριθμών είναι μαγικό τετράγωνο χρησιμοποιείται κατόπιν για την εκτίμηση του συνολικού δυνατού αριθμού των τετραγώνων.[13]
Εάν η αρίθμηση των κελιών ξεκινά από το 1, οι ελάχιστες δυνατές μαγικές σταθερές για τις πρώτες λίγες τάξεις μαγικών τετραγώνων είναι:[14]
- Τάξη 3: 15
- Τάξη 4: 34
- Τάξη 5: 65
- Τάξη 6: 111
Τύποι
[Επεξεργασία | επεξεργασία κώδικα]
Οι βασικοί τύποι μαγικών τετραγώνων ανάλογα με τους τρόπους όπου σχηματίζεται η μαγική σταθερά και την τάξη του τετραγώνου:[1]
| ημιμαγικό | το άθροισμα των γραμμών και στηλών επιστρέφει την μαγική σταθερά. |
| κανονικό | όπως το ημιμαγικό, και επιπλέον και οι διαγώνιοι τους σχηματίζουν την μαγική σταθερά, ενώ η αρίθμηση ξεκινά από το 1. |
| πανμαγικό | όπως το κανονικό, καθώς και εάν όλοι οι διαγώνιοι του (συμπεριλαμβάνοντας και τις διαγώνιους που προκύπτουν εάν λογιστεί το τετράγωνο ως συνεχής επιφάνεια από το ένα άκρο στο άλλο) ισούνται με την μαγική σταθερά. Επίσης γνωστά και ως διαβολικά μαγικά τετράγωνα ή τετράγωνα Νασίκ.[15] |
| πλήρες | όπως το πανμαγικό, και επίσης η μαγική σταθερά σχηματίζεται και από διαφορετικές υποομάδες κελιών εντός του τετραγώνου (αρτιάκις άρτια μόνο) |
| πλέον τέλειο | όπως το πλήρες, με την επιπρόσθετη ιδιότητα ότι η μαγική σταθερά σχηματίζεται από υποομάδες κελιών 2x2 (αρτιάκις άρτια μόνο) |
| πολλαπλασιασμού | αντί για πρόσθεση γίνεται η πράξη του πολλαπλασιασμού |
| πρόσθεσης-πολλαπλασιασμού | όσα τετράγωνα των οποίων η μαγική σταθερά σχηματίζεται τόσο με πρόσθεση όσο και με πολλαπλασιασμό των ίδιων αριθμών. |
| αντιμαγικά | τα αθροίσματα που προκύπτουν μεταξύ γραμμών, στηλών, και διαγωνίων, είναι όλα διαφορετικά[16] |
Σε σχέση με τα τετράγωνα που προκύπτουν από μετασχηματισμούς στους αριθμούς των κελιών υπάρχοντος τετραγώνου:[1]
| διμαγικό | εάν οι αριθμοί σε κάθε κελί αντικατασταθούν με το τετράγωνο τους και προκύπτει και πάλι μαγικό τετράγωνο |
| τριμαγικό | εάν οι αριθμοί σε κάθε κελί αντικατασταθούν με τον κύβο τους και προκύπτει και πάλι μαγικό τετράγωνο |
| προσεταιριστικό | εάν όλα τα ζεύγη των αριθμών που είναι συμμετρικά αντίθετα με το κέντρο ισούνται με n2 + 1 |
| συμπληρωματικό | το νέο μαγικό τετράγωνο που προκύπτει όταν ο αριθμός κάθε κελιού αφαιρεθεί από το n2 + 1 |
| ισότιμο | Το κάθε ένα από τα μαγικά τετράγωνα μπορούν να περιστραφούν ή να καθρεφτιστούν αναδιατάσσοντας κατάλληλα τα ψηφία τους, με τις δυνατές αυτές παραλλαγές να είναι 8. Τα τετράγωνα αυτά θεωρούνται ισότιμα και απαρτίζουν κλάση ισοδυναμίας.[17][18] |
Αδράνεια
[Επεξεργασία | επεξεργασία κώδικα]Η στιγμή αδράνειας ενός κελιού μαγικού τετραγώνου είναι το άθροισμα όλων των αριθμών των κελιών, επί το τετράγωνο της απόστασης (σε κελιά) του κελιού από το κέντρο του τετραγώνου.[11] Για παράδειγμα ένα κελί που βρίσκεται σε μια από τις γωνίες ενός τετραγώνου διαστάσεων 3×3 έχει απόσταση ίση με κελιά από το κέντρο, ενώ τα κελιά που δεν βρίσκονται στην γωνία έχουν απόσταση ίση με 1, και το κεντρικό κελί έχει απόσταση 0 από τον εαυτό του. Έτσι όλα τα μαγικά τετράγωνα κάθε τάξης διαθέτουν την ίδια στιγμή αδράνειας αναμεταξύ τους. Τα τετράγωνα τάξεως 3 έχουν όλα στιγμή αδράνειας 60, τα τάξεως 4 στιγμή αδράνειας 340, και γενικά για όλες τις διαστάσεις η τιμή ορίζεται από τον τύπο [11]
Ιστορική διαδρομή
[Επεξεργασία | επεξεργασία κώδικα]Η προέλευση των μαγικών τετραγώνων είναι η Κίνα, και μετέπειτα επεκτάθηκαν στους Ινδούς και τους Άραβες. Καθ όλη την περίοδο αυτή η χρήση τους ήταν κυρίως μυστικιστική και χρησιμοποιούνταν και ως φυλαχτά τα οποία προσέδιδαν σε αυτόν που τα φορούσε προστασία,[19] ενώ δημιουργήθηκαν και εκδοχές με γράμματα ως αριθμούς.[20] Στην Μεσαιωνική Ευρώπη, με κάποιες εξαιρέσεις όπως του Μοσχόπουλου ο οποίος ασχολήθηκε με την μαθηματική φύση των μαγικών τετραγώνων, καθώς και του Ντύρερ ο οποίος κατασκεύασε ένα εξαιρετικά σύνθετο μαγικό τετράγωνο, τα μαγικά τετράγωνα συνδέονταν κυρίως με την αστρολογία με κυρίαρχο παράδειγμα αυτό του Κορνήλιου Αγρίππα,[21][22][23]ενώ κατά την περίοδο του Διαφωτισμού και έπειτα άρχισε η συστηματική μαθηματική μελέτη τους με προεξέχων παράδειγμα τον Όιλερ.
Λούο Σου
[Επεξεργασία | επεξεργασία κώδικα]Η πρώτη εμφάνιση μαγικού τετραγώνου ανάγεται στην 3η χιλιετία π.Χ.,[24][25][26] και η προέλευση του περιγράφεται από τον κινεζικό μύθο όπου μετά από μια μεγάλη πλημμύρα που είχε σημειωθεί στον ποταμό Λούο, εμφανίστηκε μια χελώνα στον αυτοκράτορα Γου τον Μέγα η οποία είχε στο καβούκι της ένα παράξενο σχέδιο με κουκκίδες ομαδοποιημένες σε κάτι που έμοιαζε με τετραγωνική διάταξη, και τα αθροίσματα των κουκκίδων ήταν κοινά για κάθε σειρά, στήλη, και διαγώνιο. Η ακριβής χρονολόγηση της εμφάνισης του μαγικού τετραγώνου δεν είναι γνωστή, ωστόσο είναι βέβαιο ότι ήταν ευρύτερα γνωστό έως τον 5ο αιώνα π.Χ. στην Κίνα. Το σχέδιο αυτό χρησιμοποιούνταν κατόπιν αποτροπαϊκά έτσι ώστε να προσφέρει προστασία εναντίων των πλημμυρών, ενώ παράλληλα συμβόλιζε τις 2 αντίθετες δυνάμεις του γιν-γιάνγκ μαζί με τα 5 θεμελιώδη στοιχεία / Ου Σιν (μέταλλο, φωτιά, νερό, ξύλο, γη). Το τετράγωνο χρησιμοποιεί τους αριθμούς από το 1 έως το 9, είναι διαστάσεων 3x3 με μαγική σταθερά 15, και είναι γνωστό ως τετράγωνο Λούο Σου (洛书).[27]
Γιάντρα
[Επεξεργασία | επεξεργασία κώδικα]Στην ινδική παράδοση τα μαγικά τετράγωνα είναι γνωστά ως γιάντρα.[28][29]Τα πλέον γνωστά γιάντρα είναι:
- το Κατσαπούτα, το οποίο αποτελεί το παλαιότερο γνωστό παράδειγμα ινδικού μαγικού τετραγώνου χρονολογούμενο από το 550 μ.Χ., από τον αστρονόμο και μαθηματικό Βαραχαμιχίρα στο εγκυκλοπαιδικό έργο με τίτλο Μπριχάτ-Σαμίτα. Ήταν τάξης 4x4 με μαγική σταθερά 18, και χρησιμοποιήθηκε για την αναπαράσταση των αναλογιών των συστατικών σε αρώματα.[28] Η ονομασία Κατσαπούτα σημαίνει κουτί με χωρίσματα, αλλά αρχικά σήμαινε κέλυφος χελώνας όπως κατά την κινεζική παράδοση των μαγικών τετραγώνων αν και είναι αβέβαιο για το αν πράγματι προήλθε από εκεί.[30]
- το τζαϊνιστικό μαγικό τετράγωνο Τσαουτίσα Γιάντρα, στον ναό Παρσβανάθα του Κχατζουράχο, έχει διαστάσεις 4x4 με σταθερά 34, είναι πανμαγικό, και χρονολογείται από τον 12ο με 13ο αιώνα βάσει παλαιογραφικών στοιχείων.[28][31]
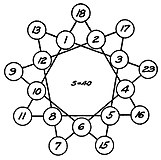
- το Κουμπέρα Κολάμ από τον ινδικό θεό του πλούτου (Κουμπέρα),[32] η χρήση τους θεωρείται ότι φέρνει ευδαιμονία, και έχουν συχνή χρήση ως διακοσμητικά σχέδια σε δάπεδα. Έχει διαστάσεις 3x3, η μαγική σταθερά του είναι 72 και οι αριθμοί των κελιών του αποτελούνται από τους αριθμούς 20 έως 28.[33][34]
- επίσης κατά την βεδική αστρολογία, τα γιάντρα αποτελούν ενεργειακά σύμβολα, και στην αριθμητική τους μορφή εκφράζονται ως μαγικά τετράγωνα μαγικής σταθεράς 15 με τον αριθμό 5 στο κέντρο τους, και συνδέονται αστρολογικά με τους πλανήτες,[35] ενώ υπάρχουν και διάφορα άλλα γιάντρα τα οποία χαράσσονται συνήθως σε δαχτυλίδια ως τυχερά σύμβολα.[36]
-
Το Τσαουτίσα Γιάντρα στον ναό Παρσβανάθα στο Κχατζουράχο, Ινδία
-
Αναπαράσταση μαγικού τετραγώνου τύπου Κουμπέρα Κολάμ
Μπουντούχ
[Επεξεργασία | επεξεργασία κώδικα]Η πρώτη γνωστή γραπτή αναφορά για μαγικά τετράγωνα στα ισλαμικά χειρόγραφα εμφανίστηκε στα γραπτά του Γκεμπέρ στις αρχές του 10ου αιώνα. Ήταν διαστάσεων 3x3 με μαγική σταθερά 15 ενώ η προέλευση τους ήταν πιθανώς κινεζική. Έγιναν γνωστά ως μπουντούχ από τα αραβικά γράμματα που χρησιμοποιούνταν ως αριθμοί στα 4 ακρογωνιαία κελιά, μπα', νταλ, ου', χα'. Τα τετράγωνα αυτά είχαν κυρίως αποτροπαϊκή χρήση ως παραστάσεις σε φυλακτά,[37][38] Με την πάροδο του χρόνου οι Άραβες κατασκεύασαν και τετράγωνα μεγαλύτερων διαστάσεων τα οποία κατά τον 19ο αιώνα έφτασαν ως και 100x100 διαθέτοντας 10.000 κελιά.[39]
-
Μαγικό τετράγωνο τύπου Μπουντούχ από αραβικό χειρόγραφο του 13ου αιώνα
Μανουήλ Μοσχόπουλος
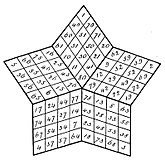
[Επεξεργασία | επεξεργασία κώδικα]Η μαθηματική πραγματεία του 1300 του Μανουήλ Μοσχόπουλου με τίτλο Παράδοσις εἴς τήν εὔρεσιν τῶν τετραγῶνων ἀριθμῶν[40] υπήρξε το έργο βάσει του οποίου η μελέτη των μαγικών τετραγώνων εισήχθηκε στην Ευρώπη,[41][42][43][25] και ορισμένες φορές αναφέρεται ως ο πρώτος γνωστός συγγραφέας που έγραψε μαθηματική μελέτη για τα μαγικά τετράγωνα,[9][44] αν και ο Κινέζος Γιάνγκ Χούι με τον οποίο έζησαν την ίδια εποχή είναι πιθανώς λίγο παλαιότερος.[45][46] Στο έργο αυτό ασχολήθηκε με την μαθηματική περιγραφή της κατασκευής των μαγικών τετραγώνων διαφόρων τάξεων (περιττές τάξεις και αρτιάκις άρτιες τάξεις διαστάσεων διαιρέσιμων με το 4).[43][25][47] Το πιθανότερο είναι πως για το έργο του αυτό βασίστηκε στα αραβικά ή περσικά γραπτά όπου η μελέτη των μαγικών τετραγώνων ήταν ανεπτυγμένη την περίοδο εκείνη, ενώ θεωρείται ελάχιστα πιθανό το να βασίστηκε σε γραπτά αρχαίων Ελλήνων συγγραφέων μια και δεν υπάρχει καμία γνωστή περίπτωση ή έμμεση περιγραφή μαγικών τετραγώνων στην κλασική, ελληνιστική, και ρωμαϊκή αρχαιότητα,[48][49] καθώς το λεγόμενο τετράγωνο του Θέωνα του Σμυρναίου δεν αποτελεί μαγικό τετράγωνο αλλά αποδόθηκε έτσι από ιστορική παραδρομή,[50][51][43][52] το ρωμαϊκό τετράγωνο SATOR αποτελεί μαγικό σύμβολο με την καθαρά αποκρυφιστική έννοια και δεν σχετίζεται με τα μαθηματικά μαγικά τετράγωνα,[53] ενώ οι εκτιμήσεις σχετικά με την πιθανή ενασχόληση των Πυθαγορείων υπάρχουν σε επίπεδο εικασίας.[9][54] Εκτός από τον Μοσχόπουλο, έχει υποστηριχτεί πως τα μαγικά τετράγωνα εμφανίζονται -ως πραγματικά μαγικά τετράγωνα αλλά με μυστικιστική χρήση- και σε ισπανικό χειρόγραφο της δεκαετίας του 1280 από τον Αλφόνσο Ι΄ τον Σοφό,[55] όπου το κάθε μαγικό τετράγωνο αντιστοιχεί σε κάποιον πλανήτη όπως στο ισλαμικό ημερολόγιο.[56]
-
Ένα από τα μαγικά τετράγωνα περιττής τάξης στα γραπτά του Μοσχόπουλου, με διαστάσεις 5x5 και μαγική σταθερά 65
Άλμπρεχτ Ντύρερ
[Επεξεργασία | επεξεργασία κώδικα]Ένα από τα πιο διάσημα μαγικά τετράγωνα του Μεσαίωνα είναι το διαστάσεων 4x4 που δημιούργησε ο Άλμπρεχτ Ντύρερ το 1514 τοποθετώντας το ως λεπτομέρεια στο χαρακτικό της Μελαγχολίας.[57]
Διαθέτει την μαγική σταθερά 34 η οποία προκύπτει από τα αθροίσματα των γραμμών, στηλών, διαγωνίων, καθώς και στις υποομάδες κελιών 2x2 που απαρτίζουν το τετράγωνο, και τους αριθμούς στις γωνίες του 4x4 τετραγώνου. Το ίδιο άθροισμα προκύπτει και με τους συνδυασμούς 3+8+14+9 και το αντίστροφο του (4 εξωτερικοί αριθμοί που σχηματίζουν νοητό κεκλιμένο τετράγωνο), τις δυο ομάδες των τεσσάρων συμμετρικών αριθμών (2+8+9+15 και 3+5+12+14), το άθροισμα των δύο μέσων καταχωρήσεων των δύο εξωτερικών στηλών και γραμμών (5+9+8+12 και 3+2+15+14), και στις τέσσερεις υποομάδες σταυροειδούς σχήματος (3+5+11+15, 2+10+8+14, 3+9+7+15, και 2+6+12+14, γνωστά ευρύτερα και ως μαγικά τετράγωνα γνώμονα[58]). Τέλος, οι 2 μεσαίοι αριθμοί στην τελευταία γραμμή του τετραγώνου (15 και 14) αντιστοιχούν στην ημερομηνία δημιουργίας του έργου, ενώ οι αριθμοί στα εξωτερικά κελιά της τελευταίας γραμμής (1 και 4) αντιστοιχούν στο πρώτο (A) και τέταρτο (D) γράμμα του λατινικού αλφαβήτου τα οποία είναι τα αρχικά του ονόματος του Ντύρερ (Albrecht Dürer).[59]
-
Η Μελαγχολία του Ντύρερ (1514), το μαγικό τετράγωνο βρίσκεται στην άνω δεξιά γωνία
-
Λεπτομέρεια του μαγικού τετραγώνου, διαστάσεων 4x4 με μαγική σταθερά 34. Οι αριθμοί στα δυο τελευταία τετράγωνα (15 και 14) ανταποκρίνονται στο έτος δημιουργίας του έργου (1514)
Κορνήλιος Αγρίππας
[Επεξεργασία | επεξεργασία κώδικα]Ο Κορνήλιος Αγρίππας ήταν φυσιοδίφης, θεολόγος, και αστρολόγος του 16ου αιώνα ο οποίος ασχολήθηκε με την κατασκευή μυστικιστικών μαγικών τετραγώνων τα οποία αναπαριστούν ουράνια σώματα του ηλιακού συστήματος (τάξεων 3, 4, 5, 6, 7, 8, και 9, για Κρόνο, Δία, Άρη, Ήλιο, Αφροδίτη, Ερμή και Σελήνη αντίστοιχα),[9][60] και θεωρούσε πως τα μαγικά τετράγωνα τάξεως 1 (1x1 κελιού) αντιπροσώπευαν την τελειότητα του Θεού.[9][61] Τα τετράγωνα αυτά είχαν ιδιαίτερη επιρροή στην Ευρώπη από τον 16ο έως τα μέσα του 17ου αιώνα, ενώ συνεχίζουν να έχουν χρήση και στην σύγχρονη εποχή στις εκάστοτε μυστικιστικές ενασχολήσεις.[62]
-
Μυστικιστικό μαγικό τετράγωνο διαστάσεων 4x4 (Δίας) με μαγική σταθερά 30
Λέοναρντ Όιλερ
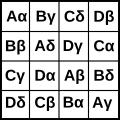
[Επεξεργασία | επεξεργασία κώδικα]Το μαγικό τετράγωνο διαστάσεων 8x8 με μαγική σταθερά 260 που κατασκεύασε ο Λέοναρντ Όιλερ είναι γνωστό και ως το μαγικό τετράγωνο των κινήσεων του ίππου (σκάκι), καθώς ξεκινώντας από το 1 και ακολουθώντας διαδοχικά το κελί του επομένου αριθμού προς την κάτω κατεύθυνση, συμπληρώνονται όλα τα κελιά μόνο μέσω κινήσεων του ίππου. Στο τετράγωνο αυτό, τα αθροίσματα των μισών γραμμών ή στηλών, ισούνται με το μισό της μαγικής σταθεράς, 260/2 = 130. Παρότι η μελέτη βάσει της οποίας προκύπτει το τετράγωνο δημιουργήθηκε από τον Όιλερ, το τετράγωνο αυτό καθεαυτό δημοσιεύτηκε έναν αιώνα αργότερα από τον Αμερικανό Ουίλιαμ Μπέβερλυ το 1848.[63]Ο Όιλερ είναι επίσης γνωστός για την εισαγωγή των ελληνολατινικών τετραγώνων (κάθε συνδυασμός ελληνικού και λατινικού γράμματος πρέπει να εμφανίζεται μόνο μια φορά) ως εργαλείο για την κατασκευή μαγικών τετραγώνων.[64][65]
-
Το μαγικό τετράγωνο που προκύπτει από τον Όιλερ, διαστάσεων 8x8 με μαγική σταθερά 260
-
Παράδειγμα ελληνολατινικού τετραγώνου όπου ο κάθε συνδυασμός των τεσσάρων ελληνικών και λατινικών γραμμάτων πρέπει να χρησιμοποιηθεί μόνο μια φορά
Βενιαμίν Φρανκλίνος
[Επεξεργασία | επεξεργασία κώδικα]Ο Βενιαμίν Φρανκλίνος ασχολήθηκε εκτεταμένα με την μελέτη των μαγικών τετραγώνων, και οι πρώτες σχετικές δημοσιεύσεις του έγιναν το 1767 όπου περιέλαβε ένα μαγικό διαστάσεων 8x8.[57] Το πιο εντυπωσιακό μαγικό τετράγωνο που συνέθεσε όμως ήταν αυτό των διαστάσεων 16x16 με μαγική σταθερά 2056, η οποία δεν προκύπτει όμως με το άθροισμα των αριθμών στις διαγώνιους. Ωστόσο, οι ξεχωριστές ιδιότητες που έχει είναι πως τα αθροίσματα των αριθμών στις μισές γραμμές ή στήλες αντιστοιχούν ακριβώς στο μισό της μαγικής σταθεράς (2056/2 = 1028), ενώ τα αθροίσματα των αριθμών σε υποομάδες γειτονικών κελιών 4x4 (16 κελιά) ισούνται με το 2056. Πέρα από αυτό, τα αθροίσματα των αριθμών στις τεθλασμένες διαγωνίους (διαγώνιος προς μια κατεύθυνση ως το μισό του τετραγώνου, και αλλαγή προς την άλλη κατεύθυνση, ως V) ισούνται επίσης με το 2056.[66]Επίσης πέρα από τα τετράγωνα κατασκεύασε και μαγικό κύκλο ο οποίος προκύπτει με το άθροισμα των αριθμών σε κάθε διαιρεμένο τμήμα του κύκλου, και παράλληλα και με το άθροισμα των αριθμών σε κάθε ομόκεντρο κύκλο, με μαγική σταθερά 360.[44]
-
Το μαγικό τετράγωνο διαστάσεων 16x16 του Φραγκλίνος με μαγική σταθερά 2056
-
Ο μαγικός κύκλος του Φραγκλίνου με μαγική σταθερά 360
Σαγράδα φαμίλια
[Επεξεργασία | επεξεργασία κώδικα]Στην ενότητα των γλυπτών των Παθών του Χριστού στον ναό της Σαγράδα Φαμίλια στην Βαρκελώνη, υπάρχει ανάγλυφο μαγικό τετράγωνο διαστάσεων 4×4. Η μαγική σταθερά του αθροίσματος των αριθμών, είναι 33, και ανταποκρίνεται στην ηλικία που είχε ο Ιησούς κατά την Σταύρωση του.[57]Οι φυσικές διαστάσεις του είναι 1x1 μέτρα, και η μαγική σταθερά προκύπτει τόσο στις γραμμές και στήλες όσο και στις διαγωνίους.[67]
-
Η θέση του τετραγώνου ανάμεσα στα γλυπτά της Σαγράδα Φαμίλια
-
Λεπτομέρεια του μαγικού τετραγώνου διαστάσεων 4x4 με μαγική σταθερά 33
Σρινιβάσα Ραμανουτζάν
[Επεξεργασία | επεξεργασία κώδικα]Ο Ινδός μαθηματικός Σρινιβάσα Ραμανουτζάν κατασκεύασε μαγικό τετράγωνο το οποίο διαθέτει την ιδιότητα πως πέρα από τα καθιερωμένα αθροίσματα γραμμών, στηλών, και διαγωνίων, περιέχει επιπλέον συνδυασμούς κελιών ώστε να επιτευχθεί η μαγική σταθερά (ως πλήρες μαγικό τετράγωνο), ενώ οι αριθμοί στην πρώτη σειρά αντιστοιχούν στην ημερομηνία γενεθλίων του (22-12-1887). Τα τετράγωνα τα οποία βασίζονται σε ημερομηνία ονομάζονται μαγικά τετράγωνα Ραμανουτζάν ή μαγικά τετράγωνα γενεθλίων.[68][69][70]
-
Διαφορετικοί τρόποι όπου προκύπτει η μαγική σταθερά 139 στο μαγικό τετράγωνο του Ραμανουτζάν. Στο τελευταίο τετράγωνο παρουσιάζεται η ημερομηνία γενεθλίων του (22 12 1887)
Μέθοδοι κατασκευής
[Επεξεργασία | επεξεργασία κώδικα]Υπάρχει ένας πολύ μεγάλος αριθμός τρόπων με τους οποίους μπορούν να κατασκευαστούν μαγικά τετράγωνα. Γενικά τα περιττής και τα αρτιάκις άρτιας τάξης είναι ευκολότερα στην κατασκευή σε σχέση με περιττής άρτιας τάξης.[71]
Ανά τάξη
[Επεξεργασία | επεξεργασία κώδικα]Τάξης 3
[Επεξεργασία | επεξεργασία κώδικα]Η πιο απλή, μη ασήμαντη (n ≠ 1) τάξη μαγικού τετραγώνου είναι η 3x3. Μπορεί να κατασκευαστεί μόνο με την χρήση τριών αρχικών -θετικών ή αρνητικών- ακεραίων α, β και γ, με τα κελιά να αποκτούν τις τιμές τους μετά από διάφορους υπολογισμούς προσθαφαίρεσης μεταξύ των ακεραίων αυτών, εφόσον α < β < γ − α και β ≠ 2α:[9]
| γ − α | γ + (α + β) | γ − β |
| (γ - β) + α | γ | (γ - α) + β |
| γ + β | γ − α − β | γ + α |
Υπάρχουν και μαγικά τετράγωνα τα οποία χρησιμοποιούν αποκλειστικά πρώτους αριθμούς, όπως το 3x3 τετράγωνο του Χένρι Έρνεστ Ντούντνεϋ (1917),[72] καθώς και το τετράγωνο του Ρούντολφ Οντρέικα (1976)[73] το οποίο χρησιμοποιεί αποκλειστικά πρώτους αριθμούς Τσεν (p + 2 είναι πρώτος ή γινόμενο πρώτων).[72] Επιπλέον, είναι δυνατά τα μαγικά τετράγωνα και με διαδοχικούς πρώτους αριθμούς όπως αυτό του Νέλσον (1994).[74]
Νέλσον
διαδοχικοί πρώτοι αριθμοί
μαγική σταθερά 4.440.084.513
| 1480028159 | 1480028153 | 1480028201 |
| 1480028213 | 1480028171 | 1480028129 |
| 1480028141 | 1480028189 | 1480028183 |
Περιττά
[Επεξεργασία | επεξεργασία κώδικα]Υπάρχουν διάφοροι τρόποι κατασκευής τετραγώνων περιττής τάξης (3x3, 5x5, 7x7 κτλ), και ένας από αυτούς είναι ο τρόπος των κινήσεων του σκακιστικού ίππου ο οποίος περιγράφτηκε μαθηματικά από τον Όιλερ αλλά οι αρχικές καταβολές του είναι αραβικές.[75] Κατά την μέθοδο αυτή, η κίνηση του ίππου είναι συνεχής προς τα κάτω δεξιά (2 κελιά κάτω, και 1 δεξιά), ενώ ο χώρος του τετραγώνου θεωρείται συνεχής (φτάνοντας στο τέλος ή άκρα του τετραγώνου οι εναπομένουσες κινήσεις γίνονται στην αρχή ή άλλη πλευρά του τετραγώνου). Εάν κάποιο κελί είναι κατειλημμένο, τότε απλώς ο αριθμός τοποθετείται 2 κελιά προς τα αριστερά από το κελί που ήδη βρίσκεται. Το ίδιο μπορεί να επιτευχθεί και από την αντίθετη κατεύθυνση, ξεκινώντας το 1 στο δεξί άνω κελί και κατόπιν έχοντας συνεχή κίνηση του ίππου προς τα κάτω αριστερά.[9]
Στο παρακάτω παράδειγμα περιττού μαγικού τετραγώνου 7x7 με μαγική σταθερά 175:
- Το 1 -> 2 -> 3 -> 4 όπως κατά την κανονική κίνηση του ίππου προς τα κάτω δεξιά, αλλά το 4 στην έβδομη σειρά συνεχίζει στο 5 στην δεύτερη σειρά
- το 7 συνεχίζει στο 8 (2 κελιά αριστερά) καθώς ο χώρος της κανονικής κίνησης είναι ήδη κατειλημμένος από το 1
- Από το 8 στο 9 γίνεται αλλαγή σειράς, και κατόπιν το 10 συνεχίζει στο 11 στην νέα σειρά αλλάζοντας παράλληλα και πλευρά
- με τον ίδιο τρόπο συμπληρώνονται όλα τα υπόλοιπα κελιά
| 1 | 25 | 49 | 17 | 41 | 9 | 33 |
| 21 | 38 | 13 | 30 | 5 | 22 | 46 |
| 34 | 2 | 26 | 43 | 18 | 42 | 10 |
| 47 | 15 | 39 | 14 | 31 | 6 | 23 |
| 11 | 35 | 3 | 27 | 44 | 19 | 36 |
| 24 | 48 | 16 | 40 | 8 | 32 | 7 |
| 37 | 12 | 29 | 4 | 28 | 45 | 20 |
Αρτιάκις άρτια
[Επεξεργασία | επεξεργασία κώδικα]Ένας από τους τρόπους κατασκευής αρτιάκις αρτίων (αρτίων διαστάσεων πολλαπλάσιων του 4, 4x4, 8x8, 12x12 κτλ) μαγικών τετραγώνων είναι χρησιμοποιώντας την μέθοδο του Ντύρερ. Ξεκινώντας από το κελί της πρώτης γραμμής και πρώτης στήλης:[9]
- συμπληρώνεται ο αρχικός αριθμός στο πρώτο άνω κελί αριστερά, και σε κατεύθυνση προς τα δεξιά, παραλείπεται η συμπλήρωση των 2 επόμενων κελιών, και συμπληρώνεται το τελευταίο κελί της γραμμής με τον αριθμό, λαμβάνοντας υπόψη τα 2 προηγούμενα ασυμπλήρωτα κελιά (n+2)
- στην επόμενη γραμμή παραλείπεται η συμπλήρωση του πρώτου κελιού δεξιά, ενώ συμπληρώνονται τα 2 επόμενα και παραλείπεται το τελευταίο
- στην επόμενη γραμμή επαναλαμβάνεται το βήμα 2
- στην επόμενη γραμμή επαναλαμβάνεται το βήμα 1
- κατόπιν τα ασυμπλήρωτα κελιά συμπληρώνονται από το τελευταίο κάτω δεξιά, από αριστερά προς δεξιά με πορεία προς τις πάνω γραμμές, με τους αριθμούς που έμειναν ασυμπλήρωτοι κατά τα προηγούμενα βήματα
- το μαγικό τετράγωνο που προκύπτει είναι πλήρες μαγικό τετράγωνο (εκτός από τις στήλες, γραμμές και διαγωνίους, τα αθροίσματα των αριθμών στις τετράδες κελιών που απαρτίζουν το συνολικό τετράγωνο, τα ακρογωνιαία κελιά, και τα κελιά με διάστημα 1 κελί οριζοντίως και καθέτως μεταξύ τους επιστρέφουν την ίδια μαγική σταθερά)
| 45→ | 46 | 47 | 48↓ |
| 49 | 50→ | 51↓ | 52 |
| 53 | 54→ | 55↓ | 56 |
| 57→ | 58 | 59 | 60 |
| 45 | 59 | ←58 | 48 |
| ↑56 | 50 | 51 | ←53 |
| ↑52 | 54 | 55 | ←49 |
| 57 | ↑47 | ←46 | 60 |
| 45 | 59 | 58 | 48 |
| 56 | 50 | 51 | 53 |
| 52 | 54 | 55 | 49 |
| 57 |
47 | 46 | 60 |
Με την ίδια λογική κατασκευάζονται και αρτιάκις άρτια τετράγωνα μεγαλυτέρων διαστάσεων, όπως 8x8 όπου ακολουθώντας την μέθοδο του Ντύρερ προκύπτει πλέον τέλειο μαγικό τετράγωνο. Tα βήματα συμπλήρωσης/μη συμπλήρωσης κελιών εφαρμόζονται σε κάθε υποενότητα 4x4, έτσι π.χ. για την 1η γραμμή συμπληρώνεται το 1 και 4, και κατόπιν το 5 και 8, ως ο πίνακας 8x8 να απαρτίζεται από 4 υποπίνακες διαστάσεων 4x4.
| 1 | 63 | 62 | 4 | 5 | 59 | 58 | 8 |
| 56 | 10 | 11 | 53 | 52 | 14 | 15 | 49 |
| 48 | 18 | 19 | 45 | 44 | 22 | 23 | 41 |
| 25 | 39 | 38 | 28 | 29 | 35 | 34 | 32 |
| 33 | 31 | 30 | 36 | 37 | 27 | 26 | 40 |
| 24 | 42 | 43 | 21 | 20 | 46 | 47 | 17 |
| 16 | 50 | 51 | 13 | 12 | 54 | 55 | 9 |
| 57 | 7 | 6 | 60 | 61 | 3 | 2 | 64 |
Περιττά άρτια
[Επεξεργασία | επεξεργασία κώδικα]Τα μαγικά τετράγωνα περιττής άρτιας τάξης (6x6, 10x10, 14x14 κτλ), θεωρούνται τα δυσκολότερα από άποψη κατασκευής. Κατά την γενική μέθοδο θεωρείται ότι το τετράγωνο περιττής άρτιας τάξης απαρτίζεται από 4 υποτετράγωνα περιττής τάξης (Α, Β, Γ, Δ) σε διαγώνια αντιστοιχία μεταξύ τους έτσι ώστε να σχηματίσουν το τελικό περιττό άρτιο τετράγωνο. Σε ότι αφορά τους αριθμούς των κελιών, η αρίθμηση του Β συνεχίζει από τον μεγαλύτερο αριθμό του Α, του Γ από το Β, και του Δ από το Γ. Κατόπιν, αντικαθιστώνται οι αριθμοί της πρώτης στήλης του Α τετραγώνου με αυτούς από το Δ τετράγωνο με εξαίρεση τους αριθμούς της μεσαίας στήλης του Α και Δ τετραγώνου οι οποίοι λογίζονται από την 2η στήλη. Παράλληλα αντικαθιστώνται και οι αριθμοί της τελευταίας στήλης του Γ τετραγώνου με αυτούς της γραμμής του Β τετραγώνου. Γενικά για κάθε τάξη τετραγώνου μεγαλύτερη από 6x6 η αντικατάσταση από τις αριστερές στήλες επεκτείνεται κατά μια στήλη, όπως και η αντικατάσταση από τις δεξιές στήλες (δεν γίνεται αντικατάσταση στα δεξιά για 6x6).[76][77]
Μετακινήσεις αριθμών στα τέσσερα 7x7 τετράγωνα
(Τετράγωνο Α = έντονη γραφή πάνω αριθμοί, Β = έντ.γραφή κάτω,
Γ = κανονική γραφή πάνω, Δ = καν.γραφή κάτω.
Με κόκκινα και πράσινα βέλη οι αντικαταστάσεις θέσεως αριθμών)
| 1↓ | 25↓ | 49↓ | 17 | 41 | 9 | 33 | 99 | 123 | 147 | 115 | 139 | 107↓ | 131↓ |
| 21↓ | 38↓ | 13↓ | 30 | 5 | 22 | 46 | 119 | 136 | 111 | 128 | 103 | 120↓ | 144↓ |
| 34↓ | 2↓ | 26↓ | 43 | 18 | 42 | 10 | 132 | 100 | 124 | 141 | 116 | 140↓ | 108↓ |
| 47 | 15↓ | 39↓ | 14↓ | 31 | 6 | 23 | 145 | 113 | 137 | 112 | 129 | 104↓ | 121↓ |
| 11↓ | 35↓ | 3↓ | 27 | 44 | 19 | 36 | 109 | 133 | 101 | 125 | 142 | 117↓ | 134↓ |
| 24↓ | 48↓ | 16↓ | 40 | 8 | 32 | 7 | 122 | 146 | 114 | 138 | 106 | 130↓ | 105↓ |
| 37↓ | 12↓ | 29↓ | 4 | 28 | 45 | 20 | 135 | 110 | 127 | 102 | 126 | 143↓ | 118↓ |
| 148↑ | 172↑ | 196↑ | 164 | 188 | 156 | 180 | 50 | 74 | 98 | 66 | 90 | 58↑ | 82↑ |
| 168↑ | 185↑ | 160↑ | 177 | 152 | 169 | 193 | 70 | 87 | 62 | 79 | 54 | 71↑ | 95↑ |
| 181↑ | 149↑ | 173↑ | 190 | 165 | 189 | 157 | 83 | 51 | 75 | 92 | 67 | 91↑ | 59↑ |
| 194 | 162↑ | 186↑ | 161↑ | 178 | 153 | 170 | 96 | 64 | 88 | 63 | 80 | 55↑ | 72↑ |
| 158↑ | 182↑ | 150↑ | 174 | 191 | 166 | 183 | 60 | 84 | 52 | 76 | 93 | 68↑ | 85↑ |
| 171↑ | 195↑ | 163↑ | 187 | 155 | 179 | 154 | 73 | 97 | 65 | 89 | 57 | 81↑ | 56↑ |
| 184↑ | 159↑ | 176↑ | 151 | 175 | 192 | 167 | 86 | 61 | 78 | 53 | 77 | 94↑ | 69↑ |
Τελικό 14x14 μαγικό τετράγωνο (σταθερά 1379)
| 148 | 172 | 196 | 17 | 41 | 9 | 33 | 99 | 123 | 147 | 115 | 139 | 58 | 82 |
| 168 | 185 | 160 | 30 | 5 | 22 | 46 | 119 | 136 | 111 | 128 | 103 | 71 | 95 |
| 181 | 149 | 173 | 43 | 18 | 42 | 10 | 132 | 100 | 124 | 141 | 116 | 91 | 59 |
| 47 | 162 | 186 | 161 | 31 | 6 | 23 | 145 | 113 | 137 | 112 | 129 | 55 | 72 |
| 158 | 182 | 150 | 27 | 44 | 19 | 36 | 109 | 133 | 101 | 125 | 142 | 68 | 85 |
| 171 | 195 | 163 | 40 | 8 | 32 | 7 | 122 | 146 | 114 | 138 | 106 | 81 | 56 |
| 184 | 159 | 176 | 4 | 28 | 45 | 20 | 135 | 110 | 127 | 102 | 126 | 94 | 69 |
| 1 | 25 | 49 | 164 | 188 | 156 | 180 | 50 | 74 | 98 | 66 | 90 | 107 | 131 |
| 21 | 38 | 13 | 177 | 152 | 169 | 193 | 70 | 87 | 62 | 79 | 54 | 120 | 144 |
| 34 | 2 | 26 | 190 | 165 | 189 | 157 | 83 | 51 | 75 | 92 | 67 | 140 | 108 |
| 194 | 15 | 39 | 14 | 178 | 153 | 170 | 96 | 64 | 88 | 63 | 80 | 104 | 121 |
| 11 | 35 | 3 | 174 | 191 | 166 | 183 | 60 | 84 | 52 | 76 | 93 | 117 | 134 |
| 24 | 48 | 16 | 187 | 155 | 179 | 154 | 73 | 97 | 65 | 89 | 57 | 130 | 105 |
| 37 | 12 | 29 | 151 | 175 | 192 | 167 | 86 | 61 | 78 | 53 | 77 | 143 | 118 |
Μετασχηματισμοί τετραγώνων σε νέα
[Επεξεργασία | επεξεργασία κώδικα]Πολλαπλασιαστικά
[Επεξεργασία | επεξεργασία κώδικα]Αντί για την πρόσθεση κάθε αριθμού σε κάθε σειρά, στήλη και διαγώνιο, στα πολλαπλασιαστικά μαγικά τετράγωνα γίνεται η πράξη του πολλαπλασιασμού, όπου το γινόμενο των αριθμών είναι κοινό μεταξύ αριθμών στηλών, γραμμών και διαγωνίων. Τα πολλαπλασιαστικά τετράγωνα μπορούν να κατασκευαστούν εύκολα παίρνοντας απλώς ένα υπάρχον μαγικό τετράγωνο και χρησιμοποιώντας τους αριθμούς που έχει ως δύναμη επί του 2 (ή όποιου άλλου αριθμού), καθώς ο λογάριθμος του γινομένου μεταξύ 2 αριθμών ισούται με το άθροισμα των λογαρίθμων των δύο αριθμών.[78]
Οι αριθμοί του αρχικού μαγικού τετραγώνου ως εκθέτες
| 24 | 29 | 22 |
| 23 | 25 | 27 |
| 28 | 21 | 26 |
Το πολλαπλασιαστικό μ. τετράγωνο που προκύπτει (σταθερά 32.768)
| 16 | 512 | 4 |
| 8 | 32 | 128 |
| 256 | 2 | 64 |
Αλφαμαγικά
[Επεξεργασία | επεξεργασία κώδικα]Ξεκινώντας από ένα αρχικό μαγικό τετράγωνο, εάν αντί για τους αριθμούς χρησιμοποιηθεί η ολόγραφη έκφραση των αριθμών, και οι αριθμοί που προκύπτουν από το άθροισμα των γραμμάτων της κάθε λέξης δημιουργούν και πάλι μαγικό τετράγωνο, τότε αυτό ονομάζεται αλφαμαγικό τετράγωνο. Η συχνότητα εμφάνισης τέτοιων τετραγώνων εξαρτάται από την εκάστοτε γλώσσα, με την γερμανική γλώσσα να διαθέτει την μεγαλύτερη συχνότητα εμφάνισης.[79][80]
| 5 | 22 | 18 |
| 28 | 15 | 2 |
| 12 | 8 | 25 |
| five | twenty-two | eighteen |
| twenty-eight | fifteen | two |
| twelve | eight | twenty-five |
| 4 | 9 | 8 |
| 11 | 7 | 3 |
| 6 | 5 | 10 |
Φιμπονάτσι
[Επεξεργασία | επεξεργασία κώδικα]Τα τετράγωνα τύπου Φιμπονάτσι δεν είναι μαγικά τετράγωνα με την κοινή έννοια του όρου καθώς τα αθροίσματα αριθμών σε κελιά γραμμών, στηλών και διαγωνίων δεν καταλήγουν σε κοινή μαγική σταθερά κάτι που έχει αποδειχθεί πως είναι αδύνατο.[81] Ωστόσο, έχουν την ιδιότητα πως το άθροισμα των γινομένων των αριθμών στις γραμμές, ισούται με το άθροισμα των γινομένων των αριθμών στις στήλες, κάτι που συμβαίνει με όλους τους αριθμούς Φιμπονάτσι αρκεί να τοποθετηθούν κατά την διάταξη κανονικού μαγικού τετραγώνου (όπως π.χ. του Λούο Σου), καθώς η ιδιότητα αυτή διατίθεται μέσω των αναλογιών των κανονικών μαγικών τετραγώνων.[6][82]
(55 x 2 x 21) + (5 x 13 x 34) + (8 x 89 x 3) = (55 x 5 x 8) + (2 x 13 x 89) + (21 x 34 x 3) = 6.656
| 55 | 2 | 21 |
| 5 | 13 | 34 |
| 8 | 89 | 3 |
Παραλλαγές
[Επεξεργασία | επεξεργασία κώδικα]Κύβοι
[Επεξεργασία | επεξεργασία κώδικα]Οι μαγικοί κύβοι αποτελούν το τρισδιάστατο εφάμιλλο των μαγικών τετραγώνων, με τις τάξεις τους να διαθέτουν 3 διαστάσεις ως n x n x n και με τα αθροίσματα να υπολογίζονται σε κάθε σειρά, στήλη (εντός επιφανείας και τις τρισδιάστατες πλευρικές), και την κάθε μια από τις 4 κύριες διαγωνίους. Εάν οι αριθμοί σε κάθε γωνία αθροίζονται επίσης στην μαγική σταθερά -οριζόμενη ως M(n)=1/2n(n^3+1)-, τότε ο κύβος είναι τέλειος μαγικός κύβος.[83]
-
3x3x3 με μαγική σταθερά 42
-
Τρισδιάστατο 6ου βαθμού (6 επιφάνειες) με την κάθε επιφάνεια να αποδίδει την σταθερά 390
Γεωμετρικά
[Επεξεργασία | επεξεργασία κώδικα]Στα γεωμετρικά -ή γεωμαγικά- τετράγωνα, γίνεται χρήση γεωμετρικών σχημάτων αντί για αριθμούς, και το τελικό σχήμα που προκύπτει από την συνένωση των σχημάτων σε κάθε σειρά, στήλη, και διαγώνιο αποτελεί επιστρέφει το ίδιο τελικό σχήμα, του οποίου τα συστατικά στοιχεία αποτελούν καθρεπτισμό των στοιχείων του σχήματος στο άλλο άκρο. Η εκδοχή αυτή είναι πολύ πρόσφατη και επινοήθηκε μόλις το 2001.[84][85]Μια άλλη εκδοχή γεωμετρικών τετραγώνων είναι τα μαγικά τετράγωνου εμβαδού, όπου ο αριθμός του κάθε κελιού προσδιορίζει το εμβαδό του ίδιου του κελιού με τα κελιά να έχουν πολύγωνο σχήμα.[86]
-
Χρήση γεωμετρικών σχημάτων αντί για αριθμούς, με την συνένωση των οποίων προκύπτει το τελικό σχήμα
-
Μαγικό τετράγωνο εμβαδού, ο αριθμός του κάθε κελιού συμβαδίζει με το εμβαδό του
Άλλες διατάξεις
[Επεξεργασία | επεξεργασία κώδικα]Υπάρχουν πολλές άλλες διατάξεις αριθμών που βασίζονται στην αρχική ιδέα του μαγικού τετραγώνου, όπου με διαφορετικούς συνδυασμούς σε διάφορες διακριτές ενότητες της διάταξης το άθροισμα των αριθμών επιστρέφει πάντα το ίδιο τελικό αποτέλεσμα. Παραδείγματα αποτελούν τα διάφορα μαγικά πολύγωνα, κύκλοι, τρίγωνα, ή και σφαίρες.[87][88]
-
Σταυροειδής διάταξη με μαγική σταθερά 1471
-
Ο Ρόμβος του Διοκλητιανού με μαγική σταθερά 162
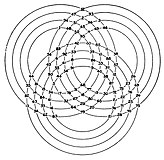
-
Τρεις ομάδες τεσσάρων ομόκεντρων κύκλων η κάθε μια με αριθμούς στα εφαπτόμενα σημεία τους, και μαγική σταθερά 776
-
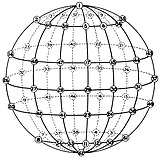
Σφαίρα κατά τον τρόπο απεικόνισης του γεωγραφικού μήκους/πλάτους της υφηλίου, με μαγική σταθερά 378
-
Το μοναδικό δυνατό μαγικό εξάγωνο (εξαιρούνται οι αντιμεταθέσεις των ίδιων αριθμών). Διαθέτει διαστάσεις 3x3 με μαγική σταθερά 38.
-
Αστρόμορφος γράφος με 9 κορυφές και μαγική σταθερά 40
Άλλες χρήσεις και αναφορές
[Επεξεργασία | επεξεργασία κώδικα]Πρακτικές εφαρμογές
[Επεξεργασία | επεξεργασία κώδικα]
Ιστορικά, ο Ινδός μαθηματικός Βαραχαμιχίρα χρησιμοποίησε μαγικά τετράγωνα τον 6ο αιώνα για την αναπαράσταση αναλογιών των συστατικών σε αρώματα.[28]
Στην σύγχρονη εποχή, τα μαγικά τετράγωνα χρησιμοποιούνται για την κρυπτογράφηση ψηφιακών εικόνων, όπου τα εικονοστοιχεία της εικόνας χωρίζονται σε ομάδες μαγικών τετραγώνων n x n διαστάσεων, οι οποίες κατόπιν μετατρέπονται σε μαγικούς κύβους n x n x n διαστάσεων και μετά από επιπλέον επεξεργασία η θέση τους αναδιατάσσεται έτσι ώστε να επιτευχθεί η κρυπτογράφηση,[89][90][91] ενώ επίσης εφαρμόζονται και σε απλούς αλγορίθμους μετάθεσης χαρακτήρων.[92]
Στην εφαρμοσμένη συνδυαστική και την μηχανική ρευστών, τα μαγικά τετράγωνα χρησιμοποιούνται για τον υπολογισμό της κατακράτησης υδάτων πάνω σε επιφάνειες. Στις περιπτώσεις αυτές ο αριθμός του κάθε κελιού λογίζεται ως το ύψος του κελιού, έτσι υπάρχουν κελιά τα οποία είναι υψηλότερα ή χαμηλότερα από άλλα. Τα κελιά τα οποία είναι χαμηλότερα από τα άλλα γειτονικά κελιά κατακρατούν νερό ίσο με την διαφορά που προκύπτει μεταξύ των αριθμητικών τιμών, ενώ τα κελιά τα οποία βρίσκονται στα άκρα του τετραγώνου δεν έχουν καθόλου κατακράτηση. Η μαγική σταθερά που επιτυγχάνεται ως προς την συνολική κατακράτηση λογίζεται ως μονάδες ύδατος.[93][94][95] Η μέγιστη δυνατή κατακράτηση μονάδων για τις λίγες πρώτες τάξεις μαγικών τετραγώνων είναι 0 μονάδες για την τάξη 3x3, 15 για 4x4, 69 για 5x5, και 192 για 6x6.[96]
Τα λατινικά τετράγωνα (τετράγωνο όπου η κάθε στήλη χρησιμοποιεί την ίδια ομάδα συμβόλων με διαφορετική διάταξη) χρησιμοποιούνται στον σχεδιασμό αγρονομικών μελετών με σκοπό την ελαχιστοποίηση σφαλμάτων.[97][98]
Άλλα
[Επεξεργασία | επεξεργασία κώδικα]Στο λογοτεχνικό έργο Φάουστ του Γκαίτε, το ξόρκι (Hexen-Einmal-Eins) το οποίο χρησιμοποιεί η μάγισσα ώστε να φτιάξει το ελιξίριο της νεότητας για τον Φάουστ, περιγράφει την διαδικασία κατασκευής μαγικού τετραγώνου.[99][100]
Η πόλη του Μακάο στην ανατολική Κίνα, εξέδωσε σειρά εννέα γραμματοσήμων το 2014 αφιερωμένη στα μαγικά τετράγωνα και την ιστορία τους.[101]
Τα σταυρόλεξα τύπου Σουντόκου είναι τύπος ημιμαγικών τετραγώνων καθώς ενώ τα αθροίσματα των στηλών και γραμμών έχουν το ίδιο σύνολο, το σύνολο αυτό δεν προκύπτει και από τα αθροίσματα των αριθμών στις διαγωνίους τους.[102][103]
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ 1,0 1,1 1,2 1,3 1,4 W., Weisstein, Eric. «Magic Square». mathworld.wolfram.com (στα Αγγλικά). Αρχειοθετήθηκε από το πρωτότυπο στις 18 Φεβρουαρίου 2019. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English. MAA. σελ. 130.
- ↑ Hawley, Del (Φεβρουάριος 2011) [Σεπτέμβριος 1998]. «Magic Squares II». NRICH.
- ↑ Allenby, R. B. J. T. (1995). Linear Algebra. σελ. 97.
- ↑ Darling, David (2004). The Universal Book of Mathematics. New Jersey: John Willey & Sons, Inc. σελ. 194. ISBN 0-471-27047-4.
- ↑ 6,0 6,1 «Magic Squares A La Fibonacci». www.pleacher.com. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ «Magic Squares which are not Normal». www.math.wichita.edu. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ «Magic Square Solver». www.gottfriedville.net. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ 9,0 9,1 9,2 9,3 9,4 9,5 9,6 9,7 Pickover, Clifford A. (2002). The Zen of Magic Squares, Circles, and Stars: An Exhibition of Surprising Structures Across Dimensions. Princeton University Press. σελ. 11 (Moschopoulos), 12 (Cornelius Agrippa), 38 (Magic square orders), 55 (Duhrer's method / Knight's move method), 63 (Other methods), 104 (Pythagorean magic squares). ISBN 9780691070414.
- ↑ «A006052 - OEIS». oeis.org. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ 11,0 11,1 11,2 Loly, Peter (Μάρτιος 2004). «The invariance of the moment of inertia of magic squares». Mathematical Gazette 88 (511): 151–153. doi:. Αρχειοθετήθηκε από το πρωτότυπο στις 2017-11-14. https://web.archive.org/web/20171114111409/http://home.cc.umanitoba.ca/~loly/MathGaz.pdf.
- ↑ Adler, Allan· Alejandre, Suzanne. «Why there are no 2x2 magic squares». mathforum.org. Αρχειοθετήθηκε από το πρωτότυπο στις 2 Μαρτίου 2018. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ Kitajima, Akimasa; Kikuchi, Macoto; Altmann, Eduardo G. (14 Μαΐου 2015). «Numerous but Rare: An Exploration of Magic Squares». PLOS ONE 10 (5): e0125062. doi:. PMID 25973764.
- ↑ «A006003 - OEIS». oeis.org. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Panmagic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 1 Ιανουαρίου 2018.
- ↑ W., Weisstein, Eric. «Antimagic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ Sallows, Lee (Fall 1997). «The lost theorem». The Mathematical Intelligencer 19 (4): 51–54. doi:. https://link.springer.com/article/10.1007%2FBF03024415#page-1.
- ↑ Swetz, Frank (2008). Legacy of the Luoshu: The 4,000 Year Search for the Meaning of the Magic Square of Order Three. CRC Press. σελ. 67.
- ↑ «Magic square | puzzle» (στα αγγλικά). Encyclopedia Britannica. https://www.britannica.com/topic/magic-square. Ανακτήθηκε στις 2017-12-17.
- ↑ "The Book of Power: Cabbalistic Secrets of Master Aptolcater, Mage of Adrianople", transl. 1724. In Shah, Idries (1957). The Secret Lore of Magic. London: Frederick Muller Ltd.
- ↑ See Juris Lidaka, The Book of Angels, Rings, Characters and Images of the Planets in Conjuring Spirits, C. Fangier ed. (Pennsylvania State University Press, 1994)
- ↑ Benedek Láng, Demons in Krakow, and Image Magic in a Magical Handbook, in Christian Demonology and Popular Mythology, Gábor Klaniczay and Éva Pócs eds. (Central European University Press, 2006)
- ↑ Drury, Nevill (1992). Dictionary of Mysticism and the Esoteric Traditions. Bridport, Dorset: Prism Press. ISBN 1-85327-075-X.
- ↑ «Magic Squares - History». plaza.ufl.edu. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ 25,0 25,1 25,2 http://www.elliepek.gr/documents/6o_synedrio_eisigiseis/Mparalhs_magika-tetragwna.pdf 3
- ↑ Gullberg, Jan (1997). Mathematics. From the Birth of Numbers. Νέα Υόρκη: W.W. Norton & Company. σελ. 205. ISBN 978-0-393-04002-9.
- ↑ 27,0 27,1 27,2 Gamwell, Lynn (2016). Mathematics + Art. A cultural history. Princeton: Princeton University Press. σελ. 40-41. ISBN 978-0-691-16528-8.
- ↑ 28,0 28,1 28,2 28,3 Selin, Helaine (31 Ιουλίου 1997). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Westen Cultures. Springer Science & Business Media. σελ. 529. ISBN 9780792340669.
- ↑ Styan, George P. H. «An introduction to Yantra magic squares and Agrippa–type magic matrices» (PDF). Mathematics and Statistics. McGill University.
- ↑ Cooke, Roger L. (14 Φεβρουαρίου 2011). The History of Mathematics: A Brief Course. John Wiley & Sons. σελ. 175. ISBN 9781118030240.
- ↑ LLP, Adarsh Mobile Applications. «Shri Lakshmi Chauntisa Yantra». www.drikpanchang.com (στα Αγγλικά). Ανακτήθηκε στις 28 Δεκεμβρίου 2017.
- ↑ Sairam, T. V. (16 Ιανουαρίου 2008). The Penguin Dictionary of Alternative Medicine. Penguin UK. ISBN 9789351181279.
- ↑ Tekriwal, Gaurav. «Dan Brown's The Lost Symbol & Indian Magic Squares | The Vedic Maths Forum India Blog». vedicmathsindia.org (στα Αγγλικά). Ανακτήθηκε στις 17 Δεκεμβρίου 2017.[νεκρός σύνδεσμος]
- ↑ Thergaonkar, Lata. Targeting Mathematics (CCE) – 8. Vikas Publishing House. ISBN 9788125950608.
- ↑ Frawley, David (1992). The Astrology of Seers: A Comprehensive Guide to Vedic Astrology. Motilal Banarsidass Publishe. σελ. 264. ISBN 9788120810075.
- ↑ Dwivedi, Dr Bhojraj (2002). Wonders of Palmistry. Diamond Pocket Books (P) Ltd. σελ. 411. ISBN 9788128400995.
- ↑ Flood, Finbarr Barry· Necipoglu, Gulru (16 Ιουνίου 2017). A Companion to Islamic Art and Architecture. John Wiley & Sons. σελ. 538. ISBN 9781119068570.
- ↑ B., Macdonald*, D.. «Budūḥ» (στα αγγλικά). Brill Reference. http://referenceworks.brillonline.com/entries/encyclopaedia-of-islam-2/buduh-COM_1395?s.num=67&s.start=60.
- ↑ «Islamic Medical Manuscripts: Glosssary of Terms». www.nlm.nih.gov. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ http://www.math.uoa.gr/me/dipl/dipl_Dragoumanioti_Vasiliki.pdf 92
- ↑ «Unity and Disunity in Mathematical Magic Squares... - ESHS». www.eshs.org (στα Αγγλικά). Αρχειοθετήθηκε από το πρωτότυπο στις 3 Δεκεμβρίου 2017. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ «illuminations.nctm.org/lesson.aspx?id=655». illuminations.nctm.org. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ 43,0 43,1 43,2 https://ac.els-cdn.com/0315086079900740/1-s2.0-0315086079900740-main.pdf?_tid=ea36c2ba-e317-11e7-ba11-00000aab0f6c&acdnat=1513507931_0d4925e6369fe91554eb85ed40993974[νεκρός σύνδεσμος] 120
- ↑ 44,0 44,1 «Magic Square». 1911 Encyclopædia Britannica Volume 17. https://en.wikisource.org/wiki/1911_Encyclop%C3%A6dia_Britannica/Magic_Square.
- ↑ Needham, Joseph (1959). Science and Civilisation in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Cambridge University Press. σελ. 61. ISBN 9780521058018.
- ↑ Joseph, George Gheverghese (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third Edition). Princeton University Press. σελ. 214. ISBN 0691135266.
- ↑ http://www.hms.gr/apothema/?s=sa&i=3498 2
- ↑ Chabert, Jean-Luc (6 Δεκεμβρίου 2012). A History of Algorithms: From the Pebble to the Microchip. Springer Science & Business Media. σελ. 64. ISBN 9783642181924.
- ↑ Sesiano, Jacques (27 Μαρτίου 2017). Magic Squares in the Tenth Century: Two Arabic Treatises by Anṭākī and Būzjānī. Springer. ISBN 9783319521145.
- ↑ Sallows, Lee C. F. (2013). Geometric Magic Squares: A Challenging New Twist Using Colored Shapes Instead of Numbers. Courier Corporation. σελ. 121. ISBN 9780486489094.
- ↑ http://euacademic.org/UploadArticle/2444.pdf 330
- ↑ Swetz, Frank (16 Ιουνίου 2008). Legacy of the Luoshu: The 4,000 Year Search for the Meaning of the Magic Square of Order Three. CRC Press. σελ. 122. ISBN 9781439865323.
- ↑ «mathforum.org/alejandre/magic.square/sator.html». mathforum.org. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ Andrews, W. S. (1917). Magic Squares and Cubes (PDF) (2η αναθεωρημένη και επαυξημένη έκδοση). Open Court Basic Readers. σελ. 146-162 (Magic squares and Pythagorean numbers).
- ↑ Alfonso X el Sabio, Astromagia (Ms. Reg. lat. 1283a), a cura di A.D'Agostino, Napoli, Liguori, 1992
- ↑ Το μαγικό τετράγωνο του Άρη εμφανίζεται στο σχήμα 1 του "Saturn and Melancholy: Studies in the History of Natural Philosophy, Religion, and Art" by Raymond Klibansky, Erwin Panofsky and Fritz Saxl, Basic Books (1964)
- ↑ 57,0 57,1 57,2 «Magic Squares - Famous Magic Squares». plaza.ufl.edu. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Gnomon Magic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 18 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Dürer's Magic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ Guiley, Rosemary (2006). The Encyclopedia of Magic and Alchemy. Infobase Publishing. σελ. 186. ISBN 9781438130002.
- ↑ «Magic Squares». Psychology Today (στα Αγγλικά). Ανακτήθηκε στις 28 Δεκεμβρίου 2017.
- ↑ «On the (magic) Square». www.cs.otago.ac.nz. Αρχειοθετήθηκε από το πρωτότυπο στις 20 Απριλίου 2018. Ανακτήθηκε στις 28 Δεκεμβρίου 2017.
- ↑ «A knight's tour magic square». www.johndcook.com (στα Αγγλικά). Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ Dunham, William (2007). The Genius of Euler: Reflections on His Life and Work. MAA. σελ. 273-276. ISBN 9780883855584.
- ↑ Bradley, Robert E.· Sandifer, Ed (20 Μαρτίου 2007). Leonhard Euler: Life, Work and Legacy. Elsevier. σελ. 401. ISBN 9780080471297.
- ↑ «Ben Franklin's Magic Square». www.math.wichita.edu. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ «Αρχειοθετημένο αντίγραφο». Αρχειοθετήθηκε από το πρωτότυπο στις 15 Σεπτεμβρίου 2011. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ «Ramanujan Magic Square - Gonit Sora» (στα αγγλικά). Gonit Sora. 2012-04-12. http://gonitsora.com/ramanujan-magic-square/. Ανακτήθηκε στις 2017-12-17.
- ↑ http://www.math.mcgill.ca/styan/Beamer3-18jan12-opt.pdf
- ↑ http://mathstimes.com/wp-content/uploads/2014/10/Birthday-magic-square.pdf
- ↑ Structure of Magic and Semi-Magic Squares, Methods and Tools for Enumeration
- ↑ 72,0 72,1 «prime magic square | planetmath.org». planetmath.org (στα Αγγλικά). Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ Heinz, Harvey. «Bibliography». recmath.org. Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Prime Magic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ Sesiano, Jacques (2003-11-01). «Construction of Magic Squares Using the Knight’s Move in Islamic Mathematics» (στα αγγλικά). Archive for History of Exact Sciences 58 (1): 1–20. doi:. ISSN 0003-9519. https://link.springer.com/article/10.1007/s00407-003-0071-4.
- ↑ «MAGIC SQUARES - Singly Even Type». www.1728.org. Ανακτήθηκε στις 31 Δεκεμβρίου 2017.
- ↑ «Magic Squares of Even orders--4n+2». www.math.wichita.edu. Ανακτήθηκε στις 31 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Multiplication Magic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ Shallows, Lee (1986). «Alphamagic Squares, Part I». Abacus: 42. http://www.leesallows.com/files/AMS%20Part%201.pdf. Ανακτήθηκε στις 1 Ιανουαρίου 2018.
- ↑ W., Weisstein, Eric. «Alphamagic Square». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 1 Ιανουαρίου 2018.
- ↑ Koshy, Thomas (24 Οκτωβρίου 2011). Fibonacci and Lucas Numbers with Applications. John Wiley & Sons. σελ. 360. ISBN 9781118031315.
- ↑ Strachan, Liz (20 Μαρτίου 2014). Numbers Are Forever. Little, Brown Book Group. σελ. 15. ISBN 9781472111104.
- ↑ W., Weisstein, Eric. «Magic Cube». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ Magic squares are given a whole new dimension, The Observer, 3 Απριλίου, 2011
- ↑ Α.Ε., tovima.gr — Δημοσιογραφικός Οργανισμός Λαμπράκη. «tovima.gr - Μαγικά τετράγωνα: τα ξαδέρφια του Sudoku». TO BHMA. Ανακτήθηκε στις 17 Δεκεμβρίου 2017.
- ↑ «Area Magic Squares». www.trump.de. Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ W., Weisstein, Eric. «Magic Figures -- from Wolfram MathWorld». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ Magic Designs, Robert B. Ely III, Journal of Recreational Mathematics volume 1 number 1, January 1968
- ↑ Niu, Wenjia· Li, Gang (7 Νοεμβρίου 2015). Applications and Techniques in Information Security: 6th International Conference, ATIS 2015, Beijing, China, 4-6 Νοεμβρίου, 2015, Proceedings. Springer. σελ. 36. ISBN 9783662486832.
- ↑ Jin, David· Lin, Sally (24 Φεβρουαρίου 2012). Advances in Electronic Commerce, Web Application and Communication. Springer Science & Business Media. σελ. 103. ISBN 9783642286582.
- ↑ Soleymani, Ali; Nordin, Md Jan; Sundararajan, Elankovan (2014). «A Chaotic Cryptosystem for Images Based on Henon and Arnold Cat Map». The Scientific World Journal 2014. doi:. ISSN 2356-6140. PMID 25258724. PMC PMC4166429. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4166429/.
- ↑ Salomon, David (6 Δεκεμβρίου 2012). Data Privacy and Security. Springer Science & Business Media. σελ. 40. ISBN 9780387217079.
- ↑ Kennard, Fredrick (21 Φεβρουαρίου 2015). Unsolved Problems in Mathematics. Lulu.com. ISBN 9781312938113.
- ↑ Koeller, Juergen. «Magic Square». www.mathematische-basteleien.de. Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ Öfverstedt, Johan (2012). Water Retention on Magic Squares with Constraint-Based Local Search (PDF). Uppsala.
- ↑ «A201126 - OEIS». oeis.org. Ανακτήθηκε στις 29 Δεκεμβρίου 2017.
- ↑ http://joas.agrif.bg.ac.rs/archive/article/59 Αρχειοθετήθηκε 2017-12-15 στο Wayback Machine. | The application of Latin square in agronomic research
- ↑ «Feature Column from the AMS» (στα αγγλικά). Feature Column from the AMS. http://www.ams.org/samplings/feature-column/fcarc-latini2. Ανακτήθηκε στις 2017-12-28.
- ↑ Bucchianeri, E. A. (2008). Faust: My Soul be Damned for the World. AuthorHouse. σελ. 198. ISBN 9781434390615.
- ↑ «Αρχειοθετημένο αντίγραφο». Αρχειοθετήθηκε από το πρωτότυπο στις 14 Ιανουαρίου 2018. Ανακτήθηκε στις 2 Ιανουαρίου 2018.
- ↑ Macau's magic square stamps just made philately even more nerdy The Guardian Science, 3 Νοεμβρίου, 2014
- ↑ «Anything but square: from magic squares to Sudoku | plus.maths.org». plus.maths.org (στα Αγγλικά). Ανακτήθηκε στις 18 Δεκεμβρίου 2017.
- ↑ Rosenhouse, Jason· Taalman, Laura (22 Δεκεμβρίου 2011). Taking Sudoku Seriously: The Math Behind the Worlds Most Popular Pencil Puzzle. Oxford University Press. ISBN 9780199913152.
Σχετική βιβλιογραφία
[Επεξεργασία | επεξεργασία κώδικα]- Block, Seymour (2009). Before Sudoku: The World of Magic Squares. Oxford University Press. ISBN 0195367901.
- McCranie, Judson (Νοέμβριος 1988). «Magic Squares of All Orders». Mathematics Teacher: 674–78.
- Ollerenshaw, Kathleen· Bree, David (Οκτώβριος 1998). Most perfect pandiagonal magic squares: their construction and enumeration. The Institute of Mathematics and its Applications. ISBN 978-0905091068.
- King, J. R. (1963). Magic Square Numbers.
- Cliff Pickover, The Zen of Magic Squares, Circles, and Stars (Princeton, New Jersey: Princeton University Press)
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]- Hawley, Del (1998). «Magic Squares». NRICH. nrich.maths.org. (περιγραφή μεθόδων κατασκευής)







![Κινεζική παράσταση του μαγικού τετραγώνου Λούο Σου, 13ος αιώνας. Η αναπαράσταση συμβολίζει τις αντίθετες δυνάμεις του θυληκού στοιχείου (Γιν, άρτια σύνολα μαύρων κουκίδων) και του αρσενικού (Γιάνγκ, περιττά σύνολα κενών κουκίδων)[27]](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e2/Magic_square_Lo_Shu.png/120px-Magic_square_Lo_Shu.png)
![Οι αριθμοί του μαγικού τετραγώνου Λούο Σου, μαγική σταθερά 15. Τα ζεύγη αριθμών ανάλογα με την διάταξη τους συμβολίζουν ένα από τα θεμελιώδη στοιχεία/Ου Σιν ([4,9] για μέταλλο, [2,7] για φωτιά, [6-1] για νερό, [8-3] για ξύλο, και στο κέντρο το 5 για την γη)[27]](http://upload.wikimedia.org/wikipedia/commons/thumb/a/af/Magic_Square_Lo_Shu.svg/120px-Magic_Square_Lo_Shu.svg.png)