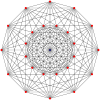
Δωδεκάγωνο
Στη γεωμετρία, το δωδεκάγωνο (από τις ελληνικές λέξεις δώδεκα και γωνία) είναι ένα οποιοδήποτε πολύγωνο σχήμα με δώδεκα πλευρές και δώδεκα κορυφές. Οι εσωτερικές γωνίες οποιουδήποτε δωδεκαγώνου έχουν άθροισμα 1800 μοίρες (°). Το σύμβολο Schläfli του δωδεκαγώνου είναι {12}.
Κανονικό δωδεκάγωνο[Επεξεργασία | επεξεργασία κώδικα]
Συνήθως ο όρος δωδεκάγωνο αναφέρεται σε ένα κανονικό δωδεκάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους. Σε ένα τέτοιο δωδεκάγωνο, οι εσωτερικές γωνίες είναι ίσες με 150° η καθεμιά.
Το εμβαδό (E) ενός κανονικού δωδεκαγώνου με μήκος πλευράς α δίνεται από τη σχέση:
Μία άλλη σχέση δίνει το εμβαδό ως συνάρτηση της ακτίνας R του περιγεγραμμένου κύκλου[1]:
- ,
ενώ αν r είναι η ακτίνα του εγγεγραμμένου κύκλου,
Απλή είναι η σχέση για το εμβαδό
,
όπου d είναι η απόσταση μεταξύ παράλληλων πλευρών ή το ύψος του σχήματος όταν το κανονικό δωδεκάγωνο στέκεται πάνω στη μία του πλευρά ως βάση (επίσης είναι η διάμετρος του εγγεγραμμένου κύκλου).
Με απλούς τριγωνομετρικούς υπολογισμούς βρίσκουμε:
.
Κατασκευή[Επεξεργασία | επεξεργασία κώδικα]
Το κανονικό δωδεκάγωνο είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη:

Η κατασκευή ενός κανονικού δωδεκαγώνου
Χρήσεις[Επεξεργασία | επεξεργασία κώδικα]
Πλακόστρωση[Επεξεργασία | επεξεργασία κώδικα]
Δίνονται τρία παραδείγματα περιοδικής πλακόστρωσης του επιπέδου που χρησιμοποιεί κανονικά δωδεκάγωνα:
 Ημικανονική πλακόστρωση 3.12.12 |
 Ημικανονική πλακόστρωση 4.6.12 |
 Ημικανονική πλακόστρωση: 3.3.4.12 & 3.3.3.3.3.3 |
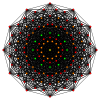
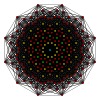
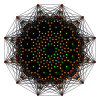
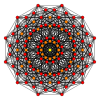
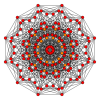
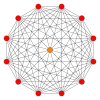
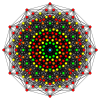
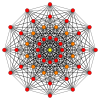
Πολύγωνα Petrie[Επεξεργασία | επεξεργασία κώδικα]
Το κανονικό δωδεκάγωνο είναι το πολύγωνο Πέτρι για πολλά πολύτοπα περισσότερων διαστάσεων, που παρατίθενται σε ορθογώνιες προβολές σε διάφορα επίπεδα Coxeter, όπως τα:
Γράμματα και κέρματα[Επεξεργασία | επεξεργασία κώδικα]

Τα «παχιά» κεφαλαία γράμματα E, Η και X (και το I σε γραμματοσειρά slab serif) έχουν δωδεκαγωνικές περιμέτρους.
Αλλά και αρκετά κέρματα έχουν δωδεκαγωνικές περιμέτρους, όπως:
- Το βρετανικό κέρμα των τριών πεννών από το 1937 ως το 1971
- Το αυστραλιανό κέρμα του μισού δολαρίου
- Τα κέρματα των 50 σεντς των Νησιών Φίτζι
- Το κέρμα των 50 σενίτι της Τόγκα (Tongan paʻanga), από το 1974
- Το κέρμα των 50 σεντς των Νησιών Σολομώντα
- Το κροατικό κέρμα των 25 κούνα
- Το Ρουμανικό κέρμα των 5000 λέι από το 2001 ως το 2005
- Το κέρμα της μιας καναδικής πέννας από το 1982 ως το 1996
- Το κέρμα των 25 đồng του Νότιου Βιετνάμ από το 1968 ως το 1975
- Το κέρμα των 50 ngwee της Ζάμπια από το 1969 ως το 1992
- Το κέρμα των 50 τάμπαλα του Μαλάουι από το 1986 ως το 1995
- Το κέρμα των 20 σεντάβος του Μεξικού από το 1992
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- δωδεκαγωνικός αριθμός
- δωδεκάεδρο – ένα κανονικό πολύεδρο με 12 πενταγωνικές έδρες.
- δωδεκάγραμμα
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Δείτε τη γεωμετρική απόδειξη του József Kürschák στο Wolfram Demonstration Project Αρχειοθετήθηκε 2018-07-31 στο Wayback Machine..
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Το θεώρημα Kürschak
- Ορισμός και ιδιότητες του δωδεκαγώνου (με διαδραστική animation)
| |||||||||||