Οκτάγωνο
| Το λήμμα παραθέτει τις πηγές του αόριστα, χωρίς παραπομπές. |
Στη γεωμετρία το οκτάγωνο (από τις ελληνικές λέξεις οκτώ και γωνία) είναι ένα πολύγωνο σχήμα με οκτώ πλευρές και οκτώ κορυφές. Σε ένα κανονικό οκτάγωνο, στο οποίο όλες οι πλευρές και όλες οι γωνίες είναι ίσες μεταξύ τους, οι γωνίες είναι ίσες με 3π/4 ακτίνια ή 135 μοίρες (°) η καθεμιά, ενώ οι εσωτερικές γωνίες οποιουδήποτε οκταγώνου έχουν άθροισμα 6π ακτίνια ή 1080 μοίρες. Το σύμβολο Schläfli του οκταγώνου είναι {8}.
Κανονικό οκτάγωνο[Επεξεργασία | επεξεργασία κώδικα]
Το κανονικό οκτάγωνο έχει οκτώ γραμμές ανακλαστικής συμμετρίας και έχει περιστροφική συμμετρία ογδόης τάξεως. Το εμβαδό (Ε) ενός κανονικού οκταγώνου με μήκος πλευράς α δίνεται από τη σχέση:
Αν R είναι η ακτίνα του περιγεγραμμένου κύκλου, τότε το εμβαδό του οκταγώνου είναι
ενώ αν r είναι η ακτίνα του εγγεγραμμένου κύκλου, τότε το εμβαδό εκφράζεται ως
Ας σημειωθεί ότι οι δύο τελευταίοι συντελεστές (2,828... και 3,31...) «περικλείουν» την τιμή του π, που είναι το εμβαδό του μοναδιαίου κύκλου.
Το εμβαδό του κανονικού οκταγώνου ισούται επίσης με:
όπου S είναι το μήκος της δεύτερης μικρότερης διαγωνίου του και α το μήκος μιας πλευράς του. Η σχέση αυτή αποδείχνεται εύκολα αν σχεδιάσουμε το περιγεγραμμένο τετράγωνο (οι 4 από τις 8 πλευρές του οκταγώνου αγγίζουν τις 4 πλευρές του τετραγώνου), πάρουμε τα γωνιακά τρίγωνα και (είναι ορθογώνια τρίγωνα με μικρές γωνίες 45°) και τα τοποθετήσουμε με τις ορθές γωνίες τους στραμμένες προς τα μέσα, σχηματίζοντας έτσι ένα τετράγωνο. Οι πλευρές αυτού του τετραγώνου είναι ίσες με αυτές του οκταγώνου.
Τα α και S συνδέονται με τη σχέση:
Μία άλλη απλή σχέση για το εμβαδό είναι
όπου d είναι η απόσταση μεταξύ δύο παράλληλων πλευρών του κανονικού οκταγώνου.
Κατασκευή[Επεξεργασία | επεξεργασία κώδικα]
 Το κανονικό οκτάγωνο είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη.
Το κανονικό οκτάγωνο είναι δυνατό να κατασκευασθεί με κανόνα και διαβήτη.
Ορθογώνιες συντεταγμένες[Επεξεργασία | επεξεργασία κώδικα]
Οι συντεταγμένες των κορυφών ενός κανονικού οκταγώνου το κέντρο του οποίου βρίσκεται στην αρχή των αξόνων και το οποίο έχει μήκος πλευράς 2, είναι:
- (±1, ±(1+√2))
- (±(1+√2), ±1).
Χρήσεις[Επεξεργασία | επεξεργασία κώδικα]
-
Οι ομπρέλες έχουν συχνά οκταγωνικό περίγραμμα.
-
Το περίφημο «κιλίμι της Μπουχάρα» περιλαμβάνει στο σχέδιό του ένα οκταγωνικό μοτίβο, το «πόδι του ελέφαντα».
-
Η ρυμοτομία του διαμερίσματος Eixample της Βαρκελώνης βασίζεται σε ακανόνιστα οκτάγωνα.
-
Το Janggi χρησιμοποιεί οκταγωνικά κομμάτια.
-
Οι ιαπωνικές μηχανές λοταρίας έχουν συχνά οκταγωνικό σχήμα.
Παράγωγα σχήματα[Επεξεργασία | επεξεργασία κώδικα]
-
`Ενα Αστεροειδές πολύγωνο, γνωστό ως οκτάγραμμα, με σύμβολο Schläfli {8/3}, εμπεριέχεται σε ένα κανονικό οκτάγωνο.
-
Το σχήμα που σχηματίζουν οι κορυφές του ομοιόμορφου πολυέδρου που ονομάζεται μέγα διρομβοεικοσιδωδεκάεδρο εμπεριέχεται σε ένα μη κανονικό οκτάπλευρο αστεροειδές πολύγωνο του οποίου 4 πλευρές περνούν από το κέντρο του.
-
Το οκταγωνικό πρίσμα περιλαμβάνει δύο οκτάγωνα.
-
The truncated square tiling has 2 octagons around every vertex.
-
Το κόλουρο κυβοκτάεδρο περιλαμβάνει 6 οκτάγωνα.
-
Το οκταγωνικό αντιπρίσμα περιλαμβάνει δύο οκτάγωνα.
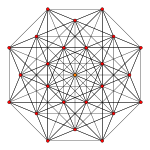
Πολύγωνα Petrie[Επεξεργασία | επεξεργασία κώδικα]
Το κανονικό οκτάγωνο είναι το πολύγωνο Πέτρι για τα παρακάτω 12 ομοιομορφικά πολύτοπα, που παρατίθενται σε ορθογώνιες προβολές σε επίπεδα Coxeter A7, B4 και D5:
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- Οκτάγραμμα
- Οκταγωνικός αριθμός
- Οκταγωνικό σπίτι
- Το Oktogon, μία μεγάλη διασταύρωση στη Βουδαπέστη
- Bumper pool
- Το Ρουμπ ελ Χιζμπ (γνωστό και ως «Αστέρι του Αλ Κουντς» ή Octa Star)
- Στρογγυλευμένο οκτάγωνο
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Οκταγωνικός υπολογιστής
- Ορισμός και ιδιότητες του οκταγώνου Με διαδραστικά animation
- Weisstein, Eric W., "Octagon" από το MathWorld.
| |||||||||||