Σπείρα του Αρχιμήδη

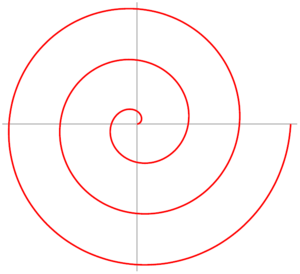
Η Σπείρα του Αρχιμήδη.

Η Σπείρα του Αρχιμήδη(παραμετρική).

Η Σπείρα του Αρχιμήδη είναι η σπειροειδής καμπύλη της οποίας χαρακτηριστικό είναι ότι η απόσταση μεταξύ δύο διαδοχικών περιελίξεων παραμένει σταθερή. Ονομάζεται και επίπεδη έλικα.

Τα σημεία της καμπύλης παράγονται από ένα σημείο το οποίο κινείται με σταθερή ταχύτητα πάνω σε μια ευθεία η οποία περιστρέφεται με σταθερή γωνιακή ταχύτητα.

Ο μαθηματικός τύπος, σε πολικές συντεταγμένες, που δίνει την καμπύλη αυτή είναι: $\,r=\alpha +\beta \theta$ , όπου $\alpha$ και $\beta$ είναι πραγματικοί αριθμοί. Αλλαγή στο $\alpha$ περιστρέφει την σπείρα, ενώ το $\beta$ καθορίζει την απόσταση μεταξύ δύο διαδοχικών περιελίξεων.

Ο Αρχιμήδης μελέτησε με μεγάλη λεπτομέρεια τις ιδιότητες της επίπεδης έλικας στο έργο του «Περί Ελίκων». Κάνοντας χρήση των γεωμτρικών ιδιοτήτων της έλικας αυτής, κατάφερε να κατασκευάσει μία λύση στο πρόβλημα του τετραγωνισμού του κύκλου, παρακάμπτοντας έτσι την "αυστηρή κατασκευή" που απαιτούσε αποκλειστικά την χρηση κανόνα και διαβήτη. Ο Αρχιμήδης θεωρείται από τους πρώτους που περιέγραψε σε αυστηρά μαθηματικό πλάισιο το συγκεκριμένο σχήμα. Αξίζει να σημειωθεί ότι υπάρχουν απεικονίσεις του συγκεκριμένου σχήματος της σπείρας ήδη από τα προϊστορικά χρόνια. Μία τέτοια χαρακτηριστική απεικόνιση αποτελεί η τοιχογραφία με τις πολύχρωμες σπείρες που βρέθηκε στο κτίριο Ξεστή 3, στον προϊστορικό οικισμό του Ακρωτηρίου της Σαντορίνης.^[1]^[2]

Αναφορές[Επεξεργασία | επεξεργασία κώδικα]

↑ Papaodysseus C., Panagopoulos Th., Exarhos M., Fragoulis D., Roussopoulos G., Rousopoulos P., Galanopoulos G., Triantafillou C., Vlachopoulos A., Doumas C.: "Distinct, Late Bronxe Age (c. 1650 bc) Wall-paintings from Akrotiri, Thera, Comprising Advanced Geometrical Patterns", Archaeometry 48 (1), 97–114 (2006).
↑ «In.gr: "Οι μαθηματικοί της Θήρας «αιώνες μπροστά από την εποχή τους»", 01.03.2006». Αρχειοθετήθηκε από το πρωτότυπο στις 20 Νοεμβρίου 2007. Ανακτήθηκε στις 4 Σεπτεμβρίου 2007.

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Σπείρα του Ούλαμ

Αυτό το λήμμα σχετικά με τη γεωμετρία χρειάζεται επέκταση. Μπορείτε να βοηθήσετε την Βικιπαίδεια επεκτείνοντάς το.

[1] Papaodysseus C., Panagopoulos Th., Exarhos M., Fragoulis D., Roussopoulos G., Rousopoulos P., Galanopoulos G., Triantafillou C., Vlachopoulos A., Doumas C.: "Distinct, Late Bronxe Age (c. 1650 bc) Wall-paintings from Akrotiri, Thera, Comprising Advanced Geometrical Patterns", Archaeometry 48 (1), 97–114 (2006).

[2] «In.gr: "Οι μαθηματικοί της Θήρας «αιώνες μπροστά από την εποχή τους»", 01.03.2006». Αρχειοθετήθηκε από το πρωτότυπο στις 20 Νοεμβρίου 2007. Ανακτήθηκε στις 4 Σεπτεμβρίου 2007.

[1]

[2]