Επαναλαμβανόμενα πλακίδια

Στη γεωμετρία της Ψηφιδοθέτησης τα Επαναλαμβανόμενα πλακίδια είναι ένα σχήμα που μπορεί να τεμαχιστεί σε μικρότερα αντίγραφα του ίδιου σχήματος. Ο αγγλικός όρος rep-tile ή reptile επινοήθηκε ως λογοπαίγνιο με τα ερπετά από τον ψυχαγωγικό μαθηματικό Σόλομον Γ. Γκόλομπ[2] και διαδόθηκε από τον Μάρτιν Γκάρντνερ στη στήλη του "Μαθηματικά παιχνίδια" στο τεύχος Μαΐου 1963 του περιοδικού Scientific American[3] . το 2012 μια γενίκευση των rep-tiles που ονομάζεται self-tiling tile sets παρουσιάστηκε από τον Λι Σάλοους στο περιοδικό Mathematics Magazine [4].


Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Ένα rep-tile ή Επαναλαμβανόμενο πλακίδιο χαρακτηρίζεται ως rep-n αν η ανατομία χρησιμοποιεί n αντίγραφα. Ένα τέτοιο σχήμα σχηματίζει αναγκαστικά το πρωτότυπο για ένα πλακίδιο του επιπέδου, σε πολλές περιπτώσεις ένα απεριοδικό πλακίδιο. Μια ανατομή με επαναληπτικά πλακίδια που χρησιμοποιεί διαφορετικά μεγέθη του αρχικού σχήματος ονομάζεται ακανόνιστο επαναληπτικό πλακίδιο ή μη επαναληπτικό πλακίδιο. Εάν η ανατομία χρησιμοποιεί n αντίγραφα, το σχήμα λέγεται ότι είναι irrep-n. Εάν όλα αυτά τα υπο-πλακίδια είναι διαφορετικού μεγέθους, τότε η πλακόστρωση περιγράφεται επιπλέον ως τέλεια. Ένα σχήμα που είναι rep-n ή irrep-n είναι κατά κανόνα irrep-(kn − k + n) για κάθε k > 1, αντικαθιστώντας το μικρότερο πλακίδιο στην rep-n' ανατομία με n ακόμα μικρότερα πλακίδια. Η σειρά ενός σχήματος, είτε χρησιμοποιείται rep-πλακίδια είτε irrep-πλακίδια, είναι ο μικρότερος δυνατός αριθμός πλακιδίων που αρκεί.
Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]

Κάθε τετράγωνο, ορθογώνιο, παραλληλόγραμμο, ρόμβος ή τρίγωνο είναι rep-4. Το σφηνοειδές ηξιαμόνδιο (που απεικονίζεται παραπάνω) είναι rep-4 και rep-9, και είναι ένα από τα λίγα γνωστά αυτοαναπαραγόμενα πεντάγωνα. Η Νησίδα Γκόσπερ είναι rep-7. Η Νιφάδα του Κοχ είναι irrep-7: έξι μικρές νιφάδες του ίδιου μεγέθους, μαζί με μια άλλη χιονονιφάδα με τριπλάσιο εμβαδόν από τις μικρότερες, μπορούν να συνδυαστούν για να σχηματίσουν μια ενιαία μεγαλύτερη χιονονιφάδα.
Ένα ορθογώνιο τρίγωνο με μήκη πλευρών στον λόγο 1:2 είναι rep-5, και η rep-5 διαίρεσή του αποτελεί τη βάση του απεριοδικού πλακιδίου pinwheel. Σύμφωνα με το Πυθαγόρειο θεώρημα, η υποτείνουσα, ή η κεκλιμένη πλευρά του τριγώνου rep-5, έχει μήκος √5.
Το διεθνές πρότυπο ISO 216 ορίζει τα μεγέθη των φύλλων χαρτιού χρησιμοποιώντας το √2, σύμφωνα με το οποίο η μεγάλη πλευρά ενός ορθογώνιου φύλλου χαρτιού είναι η τετραγωνική ρίζα του διπλάσιου της μικρής πλευράς του χαρτιού. Τα ορθογώνια σε αυτό το σχήμα είναι rep-2. Ένα ορθογώνιο (ή παραλληλόγραμμο) είναι rep-n αν ο λόγος διαστάσεων του είναι √n:1. Ένα ισοσκελές τρίγωνο είναι επίσης rep-2.
Επαναλαμβανόμενα πλακίδια και συμμετρία[Επεξεργασία | επεξεργασία κώδικα]
Ορισμένα επαναληπτικά πλακίδια, όπως το τετράγωνο και το ισόπλευρο τρίγωνο, είναι συμμετρικά και παραμένουν πανομοιότυπα όταν αντανακλώνται σε καθρέφτη. Άλλα, όπως το πλακίδιο της σφίγγας, είναι ασύμμετρα και υπάρχουν σε δύο διαφορετικές μορφές που συνδέονται με την κατοπτρική ανάκλαση. Η ανατομία της σφίγγας και ορισμένων άλλων ασύμμετρων επαναληπτικών πλακιδίων απαιτεί τη χρήση τόσο του αρχικού σχήματος όσο και της κατοπτρικής του εικόνας.
Επαναλαμβανόμενα πλακίδια και πολύμορφα[Επεξεργασία | επεξεργασία κώδικα]
Ορισμένα Επαναλαμβανόμενα πλακίδια (rep-tiles) βασίζονται σε πολυμορφές όπως τα πολυαμύγδαλα και τα τα πολυομίνια, ή σχήματα που δημιουργούνται με την τοποθέτηση ισόπλευρων τριγώνων και τετραγώνων από άκρη σε άκρη.
Τετράγωνα[Επεξεργασία | επεξεργασία κώδικα]
Αν ένα πολυόμινο είναι ορθογώνιο, δηλαδή ικανό να πλακιδώσει ένα ορθογώνιο, τότε θα είναι επίσης ένα rep-tile, επειδή το ορθογώνιο θα έχει ακέραιο λόγο μήκους πλευράς και έτσι θα πλακιδώσει ένα τετράγωνο. Αυτό μπορεί να φανεί στα οκτάμινα, τα οποία δημιουργούνται από οκτώ τετράγωνα. Δύο αντίγραφα κάποιων οκτωμίνο θα πλακιδώσουν ένα τετράγωνο- επομένως αυτά τα οκτωμίνο είναι επίσης rep-16 rep-tiles.

Τέσσερα αντίγραφα ορισμένων nonominos και nonakings σχηματίζουν ένα τετράγωνο, οπότε αυτές οι πολυμορφές είναι επίσης rep-36 rep-tiles.

Ισοσκελείς τρίγωνα[Επεξεργασία | επεξεργασία κώδικα]
Ομοίως, αν ένα πολυαμύγδαλο πλακιδώνει ένα ισόπλευρο τρίγωνο, θα είναι επίσης ένα rep-tile.

Ορθογώνια τρίγωνα[Επεξεργασία | επεξεργασία κώδικα]
Ένα ορθογώνιο τρίγωνο είναι ένα τρίγωνο που περιέχει μία ορθή γωνία 90°. Δύο συγκεκριμένες μορφές ορθογωνίου τριγώνου έχουν προσελκύσει την προσοχή των ερευνητών των ερπετών, το τρίγωνο 45°-90°-45° και το τρίγωνο 30°-60°-90°.
Τρίγωνα 45°-90°-45°[Επεξεργασία | επεξεργασία κώδικα]
Οι πολυμορφές που βασίζονται σε ισοσκελή ορθογώνια τρίγωνα, με πλευρές σε αναλογία 1 : 1 : √2, είναι γνωστές ως πολυάβολα. Ένας άπειρος αριθμός από αυτά είναι rep-tiles. Πράγματι, το απλούστερο από όλα τα rep-tiles είναι ένα απλό ισοσκελές ορθογώνιο τρίγωνο. Είναι rep-2 όταν διαιρείται από μια απλή γραμμή που διχοτομεί την ορθή γωνία με την υποτείνουσα. Τα rep-2 rep-tiles είναι επίσης rep-2n και τα rep-4,8,16+ τρίγωνα δίνουν περαιτέρω rep-tiles. Αυτά βρίσκονται απορρίπτοντας τα μισά από τα υποπολλαπλάσια και αντιμεταθέτοντας τα υπόλοιπα μέχρι να είναι κατοπτρικά συμμετρικά μέσα σε ένα ορθογώνιο τρίγωνο. Με άλλα λόγια, δύο αντίγραφα θα πλακιδώσουν ένα ορθογώνιο τρίγωνο. Ένα από αυτά τα νέα rep-tiles θυμίζει το ψάρι που σχηματίζεται από τρία ισόπλευρα τρίγωνα.
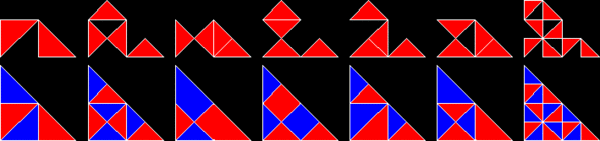
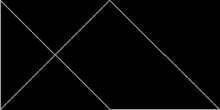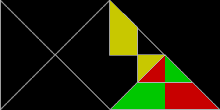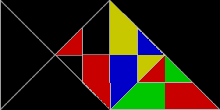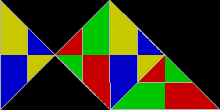
Τρίγωνα 30°-60°-90°[Επεξεργασία | επεξεργασία κώδικα]
Οι πολυμορφές που βασίζονται σε ορθογώνια τρίγωνα 30°-60°-90°, με πλευρές σε αναλογία 1 : √3} : 2, είναι γνωστές ως πολυδακτύλιοι. Ορισμένα είναι πανομοιότυπα με τα πολυμίνια και τα πολυαμίνια, άλλα είναι διαφορετικά.[5]
 |
 |
 |
 |
 |
 |
Πολλαπλά και διαφορετικά rep-tilings[Επεξεργασία | επεξεργασία κώδικα]
Πολλά από τα κοινά rep-tiles (επαναλαμβανόμενα πλακίδια) είναι rep-n2 για όλες τις θετικές ακέραιες τιμές του n. Συγκεκριμένα αυτό ισχύει για τρία τραπεζοειδή, συμπεριλαμβανομένου αυτού που σχηματίζεται από τρία ισόπλευρα τρίγωνα, για τρία παραλληλόγραμμα εξάγωνα (το L-τρομινό, το L-τετρομινό και το P-πεντόμινο) και για το σφίγγα-ηξιάμινο.[6] Επιπλέον, πολλά rep-tiles, ιδιαίτερα εκείνα με υψηλότερο rep-n, μπορούν να αυτο-τοποθετηθούν με διάφορους τρόπους. Για παράδειγμα, το rep-9 L-tetramino έχει τουλάχιστον δεκατέσσερα διαφορετικά rep-tilings. Το rep-9 σφίγγα hexiamond μπορεί επίσης να πλακοστρωθεί με διαφορετικούς τρόπους.
 |
 |
Rep-tiles με άπειρες πλευρές[Επεξεργασία | επεξεργασία κώδικα]

Τα πιο γνωστά rep-tiles (επαναλαμβανόμενα πλακίδια) είναι τα πολύγωνα με πεπερασμένο αριθμό πλευρών, αλλά ορισμένα σχήματα με άπειρο αριθμό πλευρών μπορούν επίσης να είναι επαναλαμβανόμενα πλακίδια. Για παράδειγμα, το τεραγωνικό τρίγωνο, ή κερασφόρο τρίγωνο, είναι rep-4. Είναι επίσης ένα παράδειγμα ενός φράκταλ rep-tile.
Πενταγωνικά rep-tiles[Επεξεργασία | επεξεργασία κώδικα]
Τα τριγωνικά και τετράπλευρα (τετράπλευρα) επαναληπτικά πλακίδια είναι κοινά, αλλά τα πενταγωνικά επαναληπτικά πλακίδια είναι σπάνια. Για μεγάλο χρονικό διάστημα, η σφίγγα θεωρούνταν ευρέως ότι ήταν το μοναδικό γνωστό παράδειγμα, αλλά ο Γερμανός/Νεοζηλανδός μαθηματικός Καρλ Σέρερ και ο Αμερικανός μαθηματικός Τζορτζ Σίσερμαν βρήκαν περισσότερα παραδείγματα, συμπεριλαμβανομένης μιας διπλής πυραμίδας και μιας επιμήκους εκδοχής της σφίγγας. Αυτά τα πενταγωνικά rep-tiles απεικονίζονται στις σελίδες Math Magic που εποπτεύονται από τον Αμερικανό μαθηματικό Έριχ Φρίντμαν[7]. Ωστόσο, η σφίγγα και οι εκτεταμένες εκδοχές της είναι τα μόνα γνωστά πεντάγωνα που μπορούν να rep-tiles με ίσα αντίγραφα. Βλέπε τις σελίδες του Κλαρκ για τα Reptile.
 |
Rep-tiles και φράκταλ[Επεξεργασία | επεξεργασία κώδικα]
Rep-tiles ως φράκταλ[Επεξεργασία | επεξεργασία κώδικα]
Τα rep-tiles μπορούν να χρησιμοποιηθούν για τη δημιουργία φράκταλ, ή σχημάτων που είναι αυτο-ομοειδή σε όλο και μικρότερες κλίμακες. Ένα φράκταλ rep-tile σχηματίζεται με υποδιαίρεση του rep-tile, αφαίρεση ενός ή περισσότερων αντιγράφων του υποδιαιρεμένου σχήματος και στη συνέχεια αναδρομική συνέχιση. Παραδείγματος χάριν, το χαλί Σιερπίνσκι σχηματίζεται με αυτόν τον τρόπο από την επανατοποθέτηση ενός τετραγώνου σε 27 μικρότερα τετράγωνα και το τρίγωνο Σιερπίνσκι σχηματίζεται από την επανατοποθέτηση ενός ισόπλευρου τριγώνου σε τέσσερα μικρότερα τρίγωνα. Όταν απορρίπτεται ένα υπο-κάλυμμα, ένα rep-4 L-triomino μπορεί να χρησιμοποιηθεί για τη δημιουργία τεσσάρων φράκταλ, δύο από τα οποία είναι πανομοιότυπα εκτός από τον προσανατολισμό.
 |
 |
 |
 |
Τα φράκταλ ως rep-tiles[Επεξεργασία | επεξεργασία κώδικα]
Επειδή τα φράκταλ είναι συχνά αυτοομοειδή σε όλο και μικρότερες κλίμακες, πολλά από αυτά μπορούν να αποσυντεθούν σε αντίγραφα του εαυτού τους, όπως ένα ερπετό. Ωστόσο, εάν το φράκταλ έχει κενό εσωτερικό, αυτή η διάσπαση μπορεί να μην οδηγήσει σε μια πλακόστρωση ολόκληρου του πεδίου. Παραδείγματος χάριν, το τρίγωνο Σιερπίνσκι είναι rep-3, πλακίδιο με τρία αντίγραφα του εαυτού του, και το χαλί Σιερπίνσκι είναι rep-8, πλακίδιο με οκτώ αντίγραφα του εαυτού του, αλλά η επανάληψη αυτών των αποσυνθέσεων δεν σχηματίζει πλακίδιο. Από την άλλη πλευρά, η καμπύλη του δράκου είναι μια καμπύλη που γεμίζει το χώρο με μη κενό εσωτερικό- είναι rep-4 και σχηματίζει ένα πλακάρισμα. Ομοίως, το νησί Γκόσπερ είναι rep-7, σχηματίζεται από την καμπύλη Γκόσπερ που γεμίζει το χώρο και σχηματίζει και πάλι ένα πλακίδιο.
Από την κατασκευή, κάθε φράκταλ που ορίζεται από ένα επαναληπτικό σύστημα συναρτήσεων n συσταλτών χαρτών του ίδιου λόγου είναι rep-n.
 |
 |
 |
Άπειρα πλακίδια[Επεξεργασία | επεξεργασία κώδικα]
Από τα κανονικά πολύγωνα, μόνο το τρίγωνο και το τετράγωνο μπορούν να τεμαχιστούν σε μικρότερα αντίγραφα ίσου μεγέθους. Ωστόσο, ένα κανονικό εξάγωνο μπορεί να τεμαχιστεί σε έξι ισόπλευρα τρίγωνα, καθένα από τα οποία μπορεί να τεμαχιστεί σε ένα κανονικό εξάγωνο και τρία ακόμη ισόπλευρα τρίγωνα. Αυτή είναι η βάση για μια άπειρη πλακόστρωση του εξαγώνου με εξάγωνα. Το εξάγωνο είναι επομένως ένα irrep-∞ ή irrep-άπειρο irreptile[8].
-
Κανονικό εξάγωνο με άπειρα αντίγραφα του εαυτού του
-
Μορφοκλασματική επιμήκης Νιφάδα του Κοχ (σιαμαία) με άπειρα αντίγραφα της.f[9]
Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]
- Gardner, M. (2001), «Rep-Tiles», The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, New York: W. W. Norton, σελ. 46–58
- Gardner, M. (1991), «Chapter 19: Rep-Tiles, Replicating Figures on the Plane», The Unexpected Hanging and Other Mathematical Diversions, Chicago, IL: Chicago University Press, σελ. 222–233
- Langford, C. D. (1940), «Uses of a Geometric Puzzle», The Mathematical Gazette 24 (260): 209–211, doi:
- Niţică, Viorel (2003), «Rep-tiles revisited», MASS selecta, Providence, RI: American Mathematical Society, σελ. 205–217
- Sallows, Lee (2012), «On self-tiling tile sets», Mathematics Magazine 85 (5): 323–333, doi:
- Scherer, Karl (1987), A Puzzling Journey to the Reptiles and Related Animals
- Wells, D. (1991), The Penguin Dictionary of Curious and Interesting Geometry, London: Penguin, σελ. 213–214
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- Αλγόριθμος διαμαντιού τετραγώνου
- Καμπύλη που γεμίζει το χώρο
- Νιφάδα του Κοχ
- Καμπύλη Χίλμπερτ
- Καμπύλη του δράκου
- Σπόγγος του Μένγκερ
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ «The Poly Pages». www.recmath.org. Ανακτήθηκε στις 5 Ιανουαρίου 2024.
- ↑ «Solomon W. Golomb (May 30, 1932 - May 1, 2016) | IEEE Information Theory Society». www.itsoc.org. Ανακτήθηκε στις 5 Ιανουαρίου 2024.
- ↑ A Gardner's Dozen—Martin's Scientific American Cover Stories
- ↑ Sallows (2012).
- ↑ Polydrafter Irreptiling
- ↑ Niţică (2003).
- ↑ «Math Magic, Problem of the Month (October 2002)». Αρχειοθετήθηκε από το πρωτότυπο στις 9 Δεκεμβρίου 2015. Ανακτήθηκε στις 5 Ιανουαρίου 2024.
- ↑ «Math Magic». erich-friedman.github.io. Ανακτήθηκε στις 5 Ιανουαρίου 2024.
- ↑ Pietrocola, Giorgio (2005). «Tartapelago. Arte tassellazione». Maecla.


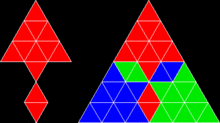

![Μορφοκλασματική επιμήκης Νιφάδα του Κοχ (σιαμαία) με άπειρα αντίγραφα της.f[9]](http://upload.wikimedia.org/wikipedia/commons/thumb/2/29/Frattale_infinito_rep-tile.gif/200px-Frattale_infinito_rep-tile.gif)