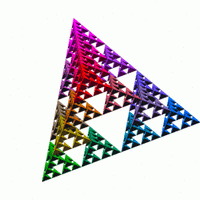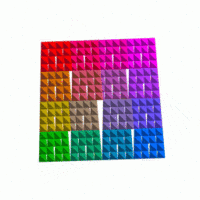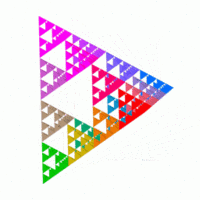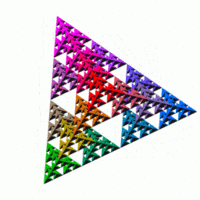Τρίγωνο Σιερπίνσκι


Το τρίγωνο Σιερπίνσκι (πολωνικά: Trójkąt Sierpińskiego, αγγλικά: Sierpinski Triangle) γνωστό και ως κόσκινο Σιερπίνσκι (Sierpinski Sieve) ή παρέμβυσμα Σιερπίνσκι (Sierpinski Gasket), είναι δομή φράκταλ σταθερού σημείου, εντός των ορίων ενός ισόπλευρου τριγώνου το οποίο διαιρείται αναδρομικά σε μικρότερα ισόπλευρα τρίγωνα. Αποτελεί ένα από τα βασικά παραδείγματα αυτοόμοιων ομάδων, όπου το σχήμα επαναλαμβάνεται σε οποιαδήποτε μεγέθυνση ή σμίκρυνση. Η ονομασία του προέρχεται από τον Πολωνό μαθηματικό Βάτσλαφ Σιερπίνσκι.[1]
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Η αρχική περιγραφή της κατασκευής έγινε από τον Βάτσλαφ Σιερπίνσκι το 1915. Παρόμοιες κατασκευές κατά το παρελθόν αποτελούν η τετρακτύς των Πυθαγορείων (6ος αιώνας π.Χ.) στα 10 πρώτα σημεία, καθώς και ψηφιδωτά του 13ου αιώνα στον καθεδρικό ναό του Ανάγκνι στην βορειοδυτική Ιταλία,[2] και σε άλλες τοποθεσίες της Ιταλίας όπως η ρωμαϊκή βασιλική της Αγίας Μαρίας στο Κοσμέντιν[3] και αλλού,[1] όπου η επανάληψη του σχεδίου γίνεται τουλάχιστον έως το 3ο επίπεδο.[4]
-
Δάπεδο εκκλησίας στην βασιλική της Αγίας Μαρίας στο Κοσμέντιν
Παρόμοιες καμπύλες μορφές προκύπτουν από το Απολλώνιο πρόβλημα, το οποίο τέθηκε από τον Απολλώνιο τον Περγαίο (3ος αιώνας π.Χ.) και στην νεότερη εποχή περιγράφθηκε από τον Γκότφριντ Λάιμπνιτζ (17ος αιώνας) και η μορφή που προκύπτει αποτελεί πρόδρομο και καμπύλη εκδοχή του τριγώνου Σιερπίνσκι.[5]
Περιγραφή[Επεξεργασία | επεξεργασία κώδικα]
Βασικές ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]

Για ακέραιο αριθμό διαστάσεων d, ο διπλασιασμός της πλευράς του αντικειμένου δημιουργεί 2d αντίγραφα του αντικειμένου αυτού, π.χ. δημιουργούνται 2 αντίγραφα για μονοδιάστατο αντικείμενο, 4 αντίγραφα για δισδιάστατο αντικείμενο, και 8 αντίγραφα για τρισδιάστατο αντικείμενο. Στα τρίγωνα Σιερπίνσκι ο διπλασιασμός της πλευράς του προκαλεί την δημιουργία 3 αντιγράφων του εαυτού του, έτσι τα τρίγωνα αυτού του τύπου διαθέτουν διάσταση Χάουσντορφ ως log(3)/log(2) = log2 3 ≈ 1,585 βάσει του 2d = 3 για το d.[6]
Το εμβαδό ενός τριγώνου Σιερπίνσκι είναι μηδέν (κατά το μέτρο Λεμπέγκ), ενώ η περιοχή που απομένει μετά από κάθε επανάληψη αποτελέι τα 34 της προηγούμενης περιοχής πριν την επανάληψη, έτσι η άπειρη επανάληψη της διαδικασίας οδηγεί στο μηδέν.[7]
Τα σημεία της δομής περιγράφονται με απλό τρόπο στις βαρυκεντρικές συντεταγμένες.[8] Εάν ένα σημείο έχει συντεταγμένες (0.u1u2u3…, 0.v1v2v3…, 0.w1w2w3…) εκφρασμένες ως δυαδικά ψηφία, τότε το σημείο βρίσκεται στο τρίγωνο Σιερπίνσκι εάν και μόνο εάν ui + vi + wi = 1 για όλα τα i.
Γενίκευση[Επεξεργασία | επεξεργασία κώδικα]
Μια γενίκευση του τριγώνου του Σιερπίνσκι αποτελεί το τρίγωνο του Πασκάλ με διαφορετικό ισοϋπόλοιπο (mod). Η επανάληψη n μπορεί να παραχθεί παίρνοντας ένα τρίγωνο Πασκάλ με Pn σειρές και χρωματίζοντας τους αριθμούς ανά την τιμή τους για x mod P. Καθώς το n προσεγγίζει το άπειρο δημιουργείται φράκταλ. Το ίδιο φράκταλ μπορεί να παραχθεί διαιρώντας ένα τρίγωνο σε ψηφιδοποίηση (tessellation) P2 παρομοίων τετραγώνων και αφαιρώντας τα ανάποδα τρίγωνα σε σχέση με το αρχικό, και κατόπιν επαναλαμβάνοντας το βήμα αυτό με κάθε μικρότερο τρίγωνο. Το φράκταλ μπορεί επίσης να δημιουργηθεί ξεκινώντας με ένα τρίγωνο και διαδοχικά τοποθετώντας τα αντίγραφα του σε διευθέτηση n(n + 1)2 κατά τον ίδιο προσανατολισμό με τα μεγαλύτερα τρίγωνα και με τις κορυφές των προηγουμένων τριγώνων να εφάπτονται.[9]
Μέθοδοι κατασκευής[Επεξεργασία | επεξεργασία κώδικα]
Αφαίρεση τριγώνων[Επεξεργασία | επεξεργασία κώδικα]
Το τρίγωνο Σιερπίνσκι μπορεί να κατασκευαστεί ξεκινώντας με ένα ισόπλευρο τρίγωνο και αφαιρώντας διαδοχικά τριγωνικά υποσύνολα από αυτό:
|
Τοπολογικά, το κάθε τρίγωνο που αφαιρείται αποτελεί ανοικτό σύνολο.[10]
Σμίκρυνση και αντιγραφή[Επεξεργασία | επεξεργασία κώδικα]
Η ίδια ακολουθία σχημάτων η οποία καταλήγει σε τρίγωνο Σιερπίνσκι μπορεί να ακολουθηθεί με τα παρακάτω βήματα:
Η παραπάνω διαδικασία δεν χρειάζεται απαραίτητα να έχει τρίγωνο, αλλά μπορεί να δουλέψει και με τετράγωνα.[11]
Παίγνιο χάους[Επεξεργασία | επεξεργασία κώδικα]
Βάσει της μεθόδου του παιγνίου χάους, εάν παρθεί ένα σημείο και κατόπιν εφαρμοστούν τυχαία κάποιοι μετασχηματισμοί σε αυτό, τα σημεία που προκύπτουν θα σχηματίσουν τρίγωνο Σιερπίνσκι:[12]
Τα παραπάνω ορίζονται από την σχέση vn+1 = 12(vn + prn), όπου rn είναι ο αριθμός 1, 2 or 3. και p1, p2 και p3 οι κορυφές του τριγώνου, ενώ vn το τυχαίο σημείο.
Καμπύλη βέλους[Επεξεργασία | επεξεργασία κώδικα]
Η δομή μπορεί να επιτευχθεί και ως καμπύλη επί πεδίου με διαδοχικές τροποποιήσεις, παρόμοιες με αυτές της Νιφάδα του Κοχ:
Το φράκταλ που προκύπτει ονομάζεται η καμπύλη βέλους Σιερπίνσκι και η οριακή μορφή του είναι το τρίγωνο Σιερπίνσκι.[13]
Άλλες μέθοδοι[Επεξεργασία | επεξεργασία κώδικα]

Η δομή μπορεί να προκύψει κατά προσέγγιση και μέσω κυτταρικών αυτομάτων, όπως το Παιχνίδι της ζωής του Κόνγουεϊ.[14][15]
Εάν παρθεί ένα τρίγωνο Πασκάλ με 2n σειρές και οι άρτιοι αριθμοί χρωματιστούν λευκοί ενώ οι περιττοί μαύροι, το αποτέλεσμα που προκύπτει είναι τρίγωνο Σιερπίνσκι καθώς αντιστοιχεί στο όριο ακολουθίας όπου το n προσεγγίζει το άπειρο κατά την εναλλαγή περιττών και άρτιων.[16]
Στο παιχνίδι του πύργου του Ανόι, γίνεται μετακίνηση δίσκων μεταξύ τριών δοκών, εφόσον ο κάθε δίσκος είναι μικρότερος από αυτόν που βρίσκεται ακριβώς από κάτω του. Η ακολουθία κινήσεων εκφραζόμενη ως μη κατευθυνόμενο γράφημα, μπορεί να εκφραστεί γεωμετρικά ως το γράφημα τομής της ομάδος των τριγώνων που απομένουν μετά το νιοστό βήμα κατά την κατασκευή του τριγώνου του Σιερπίνσκι, και η ακολουθία των γραφημάτων αυτών αποτελεί διακριτό ανάλογο του τριγώνου του Σιερπίνσκι.[17]
Τέτριξ[Επεξεργασία | επεξεργασία κώδικα]
Το τετράεδρο Σιερπίνσκι ή τέτριξ αποτελεί την τρισδιάστατη μορφή του τριγώνου. Σχηματίζεται με την σμίκρυνση ενός κανονικού τετράεδρου σε 1/2 του αρχικού του ύψους, και τοποθετώντας 4 αντίγραφα του τετράεδρου με τις γωνίες τους να εφάπτονται, και η διαδικασία αυτή επαναλαμβάνεται διαδοχικά. Η ίδια διαδικασία μπορεί να εφαρμοστεί και επί τετράγωνης πυραμίδας χρησιμοποιώντας 5 αντί για 4 αντίγραφα.[18][19]
-
Τρισδιάστατο τρίγωνο Σιερπίνσκι και το αντίστροφο του.
-
Περιστρεφόμενη τέτριξ και οι ορθογραφικές προβολές της
-
Τετράεδρο Σιερμπίνσκι πυραμίδας
Κατά την διαδικασία αυτή το συνολικό εμβαδό της επιφάνειας παραμένει σταθερό μετά την κάθε επανάληψη. Το αρχικό εμβαδό επιφανείας του τετράεδρου με μήκος πλευράς L είναι L2√3, και κατά το επόμενο βήμα υπάρχουν 4 αντίγραφα με μήκος πλευράς L/2 και έτσι το συνολικό εμβαδό γίνεται 4(L/2)2√3 = 4L2√3/4 = L2√3 ξανά.[19]
Προγραμματιστικά[Επεξεργασία | επεξεργασία κώδικα]

Στην γλώσσα προγραμματισμού που διατίθεται εντός του λογισμικού μαθηματικών υπολογισμών Mathematica, η αναδρομική συνάρτηση SiPyramid παράγει τρισδιάστατη πυραμίδα αυθαιρέτου βαθμού n ως το εμφανιζόμενο γραφικό αντικείμενο Graphics3D:
vect[1] = {0, 0, 0};
vect[2] = {1, 0, 0};
vect[3] = {0.5, 3^0.5/2, 0};
vect[4] = {0.5, 1/3*3^0.5/2, ((3^0.5/2)^2 - (1/3*3^0.5/2)^2)^0.5};
Tetron[{i_, j_, k_}] :=
Tetrahedron[{vect[1] + {i, j, k}, vect[2] + {i, j, k}, vect[3] + {i, j, k}, vect[4] + {i, j, k}}];
SiPyramid[0, {i_, j_, k_}] := {Tetron[{i, j, k}]};
SiPyramid[n_, {i_, j_, k_}] :=
Module[{s = {}},
Do[s = Union[s,
SiPyramid[n - 1, 2^(n - 1)*vect[u] + {i, j, k}]], {u, 4}]; s];
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 Conversano, Elisa; Tedeschini-Lalli, Laura (2011), «Sierpinski Triangles in Stone on Medieval Floors in Rome», APLIMAT Journal of Applied Mathematics 4: 114, 122, http://www.formulas.it/formulog/wp-content/uploads/2014/12/sierpinski-aplimat.pdf
- ↑ Wolfram, Stephen (2002), A New Kind of Science, Wolfram Media, σελ. 43, 873
- ↑ "Geometric floor mosaic (Sierpinski triangles), nave of Santa Maria in Cosmedin, Forum Boarium, Rome", 5 September 2011, Flickr
- ↑ Benedetto, John· Wojciech, Czaja. Integration and Modern Analysis. σελ. 408.
- ↑ Mandelbrot B (1983). The Fractal Geometry of Nature. New York: W. H. Freeman. σελ. 170. ISBN 978-0-7167-1186-5.
Aste T, Weaire D (2008). In Pursuit of Perfect Packing (2nd έκδοση). New York: Taylor and Francis. σελίδες 131–138. ISBN 978-1-4200-6817-7. - ↑ Falconer, Kenneth (1990). Fractal geometry: mathematical foundations and applications. Chichester: John Wiley. σελ. 120. ISBN 0-471-92287-0. Zbl 0689.28003.
- ↑ Helmberg, Gilbert (2007), Getting Acquainted with Fractals, Walter de Gruyter, σελ. 41, ISBN 9783110190922, https://books.google.com/books?id=PbrlYO83Oq8C&pg=PA41.
- ↑ http://www.cut-the-knot.org/ctk/Sierpinski.shtml
- ↑ Shannon & Bardzell, Kathleen & Michael, Patterns in Pascal's Triangle - with a Twist - First Twist: What is It?, Mathematical association of America, http://www.maa.org/publications/periodicals/loci/joma/patterns-in-pascals-triangle-with-a-twist-first-twist-what-is-it, ανακτήθηκε στις 29 March 2015
- ↑ "Sierpinski Gasket by Trema Removal"
- ↑ Michael Barnsley, V-variable fractals and superfractals, http://www.maths.anu.edu.au/~barnsley/pdfs/V-var_super_fractals.pdf, ανακτήθηκε στις 2017-12-16
- ↑ Feldman, David P. (2012), «17.4 The chaos game», Chaos and Fractals: An Elementary Introduction, Oxford University Press, σελ. 178–180, ISBN 9780199566440, https://books.google.com/books?id=exnWM_ZHK0MC&pg=PA178.
- ↑ Prusinkiewicz, P. (1986), «Graphical applications of L-systems», Proceedings of Graphics Interface '86 / Vision Interface '86, σελ. 247–253, https://blog.itu.dk/mpgg-e2012/files/2012/09/graphicalgi86.pdf, ανακτήθηκε στις 2017-12-16.
- ↑ Rumpf, Thomas (2010), «Conway's Game of Life accelerated with OpenCL», Proceedings of the Eleventh International Conference on Membrane Computing (CMC 11), σελ. 459–462, http://cmc11.uni-jena.de/proceedings/rumpf.pdf, ανακτήθηκε στις 2017-12-16.
- ↑ Bilotta, Eleonora; Pantano, Pietro (Summer 2005), «Emergent patterning phenomena in 2D cellular automata», Artificial Life 11 (3): 339–362, doi:.
- ↑ Stewart, Ian (2006), How to Cut a Cake: And other mathematical conundrums, Oxford University Press, σελ. 145, ISBN 9780191500718, https://books.google.com/books?id=theofRmeg0oC&pg=PT145.
- ↑ Romik, Dan (2006), «Shortest paths in the Tower of Hanoi graph and finite automata», SIAM Journal on Discrete Mathematics 20 (3): 610–62, doi:.
- ↑ W., Weisstein, Eric. «Tetrix». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 16 Δεκεμβρίου 2017.
- ↑ 19,0 19,1 Landman, Bruce· Nathanson, Melvyn B. (1 Ιανουαρίου 2007). Combinatorial Number Theory: Proceedings of the 'Integers Conference 2005' in Celebration of the 70th Birthday of Ronald Graham, Carrollton, Georgia, October 27-30, 2005. Walter de Gruyter. σελ. 213. ISBN 9783110925098.
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- (Αγγλικά) Pythagorean triangles, Waclaw Sierpinski, Courier Corporation, 2003
- (Αγγλικά) Hazewinkel, Michiel, επιμ.. (2001), «Sierpinski gasket», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/s130310
- (Αγγλικά) Weisstein, Eric W., "Sierpinski Sieve" από το MathWorld.
- (Αγγλικά) Real-time GPU generated Sierpinski Triangle in 3D
|