Υπερορθογώνιο
| Υπερορθογώνιο ν-ορθότοπο | |
|---|---|
 Το κυβοειδές ορθογώνιο είναι 3-ορθότοπο | |
| Τύπος | Πρίσμα |
| Όψεις | 2ν |
| Κορυφές | 2ν |
| Συμμετρία | [2ν-1], τάξη 2ν |
| Schläfli | { }n |
| Coxeter-Dynkin | |
| Διπλό πολύτοπο | Ορθογώνιο ν-fusil |
| Ιδιότητες | κυρτό, ζωνόεδρο, ισογώνιο |
Στην γεωμετρία, ένα ορθότοπο,[1][2] που επίσης ονομάζεται Υπερορθογώνιο, είναι μια γενίκευση του ορθογωνίου όσο αναφορά τις περισσότερες από δύο διαστάσεις του, επισήμως ορίζεται ως το Καρτεσιανό γινόμενο των ευθύγραμμων τμημάτων του. Ένα ορθότοπο τριών διαστάσεων καλείται επίσης ακριβές ορθογώνιο πρίσμα, ορθογώνιο κυβοειδές, ή ορθογώνιο παραλληλεπίπεδο.[3]
Μια ειδική περίπτωση ν-ορθότοπου, όπου όλες οι ακμές του είναι ίσες, καλείται ν-υπερκύβος.[1]
Διπλό πολύτοπο
[Επεξεργασία | επεξεργασία κώδικα]Το Διπλό πολύτοπο ενός ν-ορθότοπου έχει ποικιλοτρόπως ονομαστεί ως ορθογώνιο (ν-orthoplex), ρομβοειδές (ν-fusil), ή παστίλια (ν-lozenge). Είναι κατασκευασμένο από 2ν σημεία που βρίσκονται στο κέντρο των ορθογώνιων επιφανειών του ορθότοπου. Τα σχήματα των επίπεδων που διασταυρώνονται σε όλα τα ζεύγη των αξόνων του είναι ρόμβοι. Ο συμβολισμός Schläfli για το ν-fusil αντιπροσωπεύεται από το άθροισμα των ν-ορθογώνιων ευθύγραμμων τμημάτων: { } + { } + ... + { }
| n | Παράδειγμα |
|---|---|
| 1 |  { } |
| 2 | 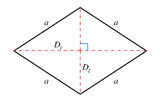 { } + { } |
| 3 | 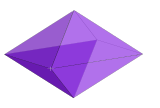 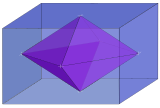 Παράδειγμα ρομβοειδές 3-orthoplex εσωτερικά κυβοειδές 3-ορθότοπο { } + { } + { } |
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]Πηγές
[Επεξεργασία | επεξεργασία κώδικα]- Coxeter, Harold Scott MacDonald (1973). Regular Polytopes (3η έκδοση). Νέα Υόρκη: Dover. σελίδες 122-123. ISBN 0-486-61480-8.

