Ισογώνιο σχήμα
Στη γεωμετρία, ένα πολύτοπο (για παράδειγνα πολύγωνο ή πολύεδρο) είναι ισογώνιο ή έχει μεταβατικότητα κορυφών εάν, μιλώντας αόριστα, όλες οι κορυφές του είναι ίδιες. Αυτό σημαίνει ότι κάθε κορυφή είναι περιτριγυρισμένη από ίδιου είδους επιφάνειες με ίδια ή αντίστροφη σειρά, και με ίδιες γωνίες μεταξύ των αντίστοιχων επιφανειών.
Τεχνικά, μπορούμε να πούμε ότι για οποιεσδήποτε δύο κορυφές υπάρχει μια συμμετρία του πολυτόπου η οποία απεικονίζει την πρώτη κορυφή ισομετρικά πάνω στη δεύτερη. Κάποιοι άλλοι τρόποι για να το εκφράσουμε είναι ότι η ομάδα του αυτομορφισμού του πολυτόπου είναι μεταβατική στις κορυφές του, ή ότι οι κορυφές του βρίσκονται μέσα σε μία και μόνο τροχιά συμμετρίας.
Όλες οι κορυφές ενός πεπερασμένου ν-διαστάσεων ισογωνίου σχήματος υφίστανται πάνω σε μια (ν-1)-σφαίρα.
Ο όρος ισογώνιο χρησιμοποιείται από καιρό για τα πολύεδρα. Η μεταβατικότητα κορυφών είναι ένα συνώνυμο και δάνειο από σύγχρονες ιδέες, όπως οι συμμετρικές ομάδες και η θεωρία γραφημάτων.
Το ψευδορομβοκυβοκτάεδρο, το οποίο δεν είναι ισογώνιο, καταδεικνύει απλώς τον ισχυρισμό ότι «όλες οι κορυφές του δείχνουν ίδιες» και αυτό δεν είναι τόσο περιοριστικό όσο ο ορισμός που χρησιμοποιείται εδώ, ο οποίος περιλαμβάνει και την ομάδα ισομετριών που διατηρείται στο πολύεδρο και την ψηφοθέτηση.
Ισογώνια πολύγωνα και απειρογώνια
[Επεξεργασία | επεξεργασία κώδικα]| Ισογώνια απειρογώνια |
|---|
| Ισογώνια λοξά απειρογώνια |

|
Όλα τα κανονικά πολύγωνα, απειρογώνια και κανονικά αστεροειδείς πολύγωνα είναι ισογώνια. Το διπλό του ισογώνιου πολυγώνου είναι ένα ισότοξο πολύγωνο.
Μερικά πολύγωνα και απειρογώνια με ζυγό αριθμό εδρών, που εναλλάσσουν δύο μήκη ακμών (για παράδειγμα το ορθογώνιο), είναι ισογώνια.
Όλες τα επίπεδα ισογώνια 2ν-γώνια έχουν δίεδρη συμμετρία (Dν, ν=2,3,...) με γραμμές ανάκλασης πάνω σε όλα τα σημεία της μέσης ακμής.
| D2 | D3 | D4 | D7 |
|---|---|---|---|
 Τα ισογώνια ορθογώνια και σταυρωτά ορθογώνια μοιράζονται την ίδια κορυφή διευθέτησης |
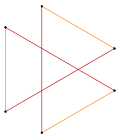 Ισογώνιο εξάγραμμο με 6 ταυτόσημες κορυφές και 2 μήκη ακμής[1] |
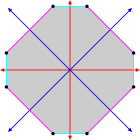 Ισογώνιο κυρτό οκτάγωνο με μπλε και κόκκινες ακτινωτές γραμμές ανάκλασης |
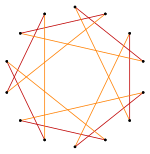 Ισογώνιο "άστρο" τετραδεκάγωνο με έναν τύπο κορυφής, και δύο τύπους ακμής[2] |
Ισογώνια πολύεδρα και ψηφοθέτηση δύο διαστάσεων
[Επεξεργασία | επεξεργασία κώδικα] Αυτό το λήμμα χρειάζεται μετάφραση.
Αν θέλετε να συμμετάσχετε, μπορείτε να επεξεργαστείτε το λήμμα μεταφράζοντάς το ή προσθέτοντας δικό σας υλικό και να αφαιρέσετε το {{μετάφραση}} μόλις το ολοκληρώσετε. Είναι πιθανό (και επιθυμητό) το ξενόγλωσσο κείμενο να έχει κρυφτεί σαν σχόλιο με τα <!-- και -->. Πατήστε "επεξεργασία" για να δείτε ολόκληρο το κείμενο. |
Ισογώνια πολύτοπα και ψηφοθετήσεις ν-διαστάσεων
[Επεξεργασία | επεξεργασία κώδικα]Οι ορισμοί αυτοί μπορούν να επεκταθούν σε υψηλότερες διαστάσεις πολυτόπων και ψηφοθετήσεων. Πιο γενικά, όλα τα ομοιόμορφα πολύτοπα είναι ισογώνια.
Το διπλό ενός ισογώνιου πολυτόπου ονομάζεται ισότοπο το οποίο είναι μεταβατικό στις όψεις του.
k-ισογώνια και k-ομοιόμορφα σχήματα
[Επεξεργασία | επεξεργασία κώδικα]Ένα πολύτοπο ή ψηφιδωτό μπορεί να ονομάζεται k-ισογώνιο σχήμα αν οι κορυφές του αποτελούν k μεταβατικές τάξεις. Ένας πιο περιοριστικός όρος, είναι το k-ομοιόμορφο σχήμα που ορίζεται ως ένα k-ισογώνιο σχήμα το οποίο κατασκευάζεται μόνο από κανονικά πολύγωνα. Μπορούν να αναπαρίστανται οπτικά με χρώματα από διαφορετικούς ομοιόμορφους χρωματισμούς.
 |
 |
 |
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Coxeter, Harold Scott MacDonald. The Densities of the Regular Polytopes II, σσ. 54-55, "hexagram" vertex figure of h{5/2,5}
- ↑ Grünbaum, Branko (1994). The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, Metamorphoses of polygons, Figure 1. Parameter t=2.0
Βιβλιογραφία
[Επεξεργασία | επεξεργασία κώδικα]- Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. ISBN 0-521-55432-2. (σελ. 369 Transitivity)
- Grünbaum, Branko· Shephard, G. C. (1987). Tilings and Patterns. W. H. Freeman & Company. ISBN 0-7167-1193-1. (σελ. 33 k-isogonal tiling, σελ. 65 k-uniform tilings)
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]- Weisstein, Eric W., "Vertex-transitive graph" από το MathWorld.
- Weisstein, Eric W., "Demiregular tessellations" από το MathWorld. (Also uses term k-uniform for k-isogonal)
- Vladimir L. Bulatov, Isogonal Kaleidoscopical Polyhedra, Physics Department, Oregon State University, Corvallis, Presented at Mosaic2000, Millennial Open Symposium on the Arts and Interdisciplinary Computing, 21–24 August 2000, Seattle, WA VRML models
- Steven Dutch uses the term k-uniform for enumerating k-isogonal tilings
- List of n-uniform tilings
