Γωνιακή συχνότητα
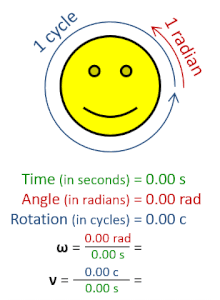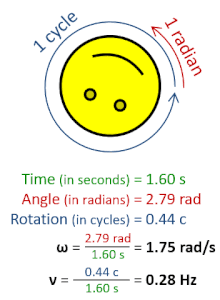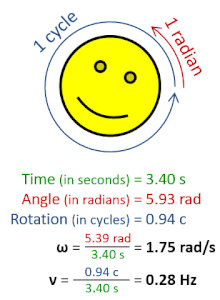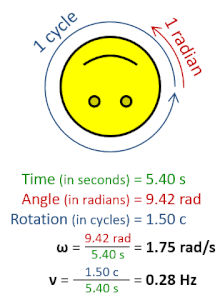
Στη φυσική, η γωνιακή συχνότητα ω (αναφέρεται και ως γωνιακή ταχύτητα, κυρίως για την περιστροφική κίνηση) είναι το βαθμωτό μέγεθος της γωνιακής μετατόπισης ανά μονάδα χρόνου (π.χ. στις περιστροφικές κινήσεις) ή του ρυθμού μεταβολής της φάσης ενός ημιτονοειδούς κύματος (π.χ. σε ταλαντώσεις και κύματα). Η γωνιακή συχνότητα συνιστά μέτρο της ψευδοδιανυσματικής ποσότητας της γωνιακής ταχύτητας.[1]
| Κλασική μηχανική |
|---|
Μία πλήρης στροφή ισούται με ακτίνια, εξού και ο μαθηματικός τύπος της γωνιακής συχνότητας:[1][2]όπου είναι η γωνιακή συχνότητα σε ακτίνια ανά δευτερόλεπτο, είναι η περίοδος σε δευτερόλεπτα και είναι η συχνότητα σε χερτζ (ενίοτε η συχνότητα συμβολίζεται με το γράμμα ν).
Μονάδες
[Επεξεργασία | επεξεργασία κώδικα]Στο διεθνές σύστημα μονάδων SI, η γωνιακή συχνότητα αποδίδεται συνήθως σε ακτίνια ανά δευτερόλεπτο, ακόμη και όταν δεν χρησιμοποιείται για την περιγραφή κάποιας περιστροφικής κίνησης.
Η μονάδα Hertz (Hz) είναι διαστατικά ισοδύναμη, αλλά κατά σύμβαση χρησιμοποιείται μόνο για τη συχνότητα, , ποτέ για τη γωνιακή συχνότητα , προς αποφυγή σύγχυσης[3] (σημειωτέον ότι το ακτίνιο συχνά παραλείπεται κατά την έκφραση μεγεθών σε μονάδες SI.[4][5]
Παραδείγματα
[Επεξεργασία | επεξεργασία κώδικα]
Κυκλική κίνηση
[Επεξεργασία | επεξεργασία κώδικα]Για ένα αντικείμενο που περιστρέφεται η βρίσκεται σε τροχιά, η απόστασης από τον άξονα περιστροφής, , η εφαπτομενική ταχύτητα, , και η γωνιακή συχνότητα της περιστροφής σχετίζονται.
Ειδικότερα, κατά τη διάρκεια μιας περιόδου, , ένα σώμα σε κυκλική κίνηση διανύει απόσταση . Η απόσταση αυτή ισούται με τη συνολική διαδρομή που διανύεται από το σώμα, . Εξισώνοντας τις δύο ποσότητες και χρησιμοποιώντας τη σχέση μεταξύ περιόδου και γωνιακής συχνότητας, , λαμβάνουμε τη σχέση:
Απλή αρμονική ταλάντωση
[Επεξεργασία | επεξεργασία κώδικα]Έστω ένα αντικείμενο που ταλαντώνεται γύρω από μία θέση ισορροπίας και μεταξύ δύο ακραίων θέσεων, όντας συνδεδεμένο σε ιδανικό ελατήριο αμελητέας μάζας και μηδαμινής απόσβεσης. Η κίνηση αυτή ονομάζεται απλή αρμονική ταλάντωση και η γωνιακή της συχνότητα δίνεται από τον τύπο:[6]
όπου είναι η σταθερά του ελατηρίου και είναι η μάζα του αντικειμένου. Η επιτάχυνση του αντικειμένου μπορεί να υπολογιστεί με τον τύπο:
όπου το είναι η μετατόπιση από τη θέση ισορροπίας. Χρησιμοποιώντας τη συχνότητα , η εξίσωση γίνεται:
Κυκλώματα LC
[Επεξεργασία | επεξεργασία κώδικα]Η γωνιακή συχνότητα συντονισμού σε ένα κύκλωμα LC σειράς ισούται με την τετραγωνική ρίζα του πολλαπλασιαστικού αντιστρόφου του γινομένου της χωρητικότητας ( σε φαράντ) επί της αυτεπαγωγής του κυκλώματος (, σε henry):[7]
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ 1,0 1,1 Cummings, Karen· Halliday, David (2007). Understanding physics (στα Αγγλικά). New Delhi: John Wiley & Sons, authorized reprint to Wiley – India. σελίδες 449, 484, 485, 487. ISBN 978-81-265-0882-2.
- ↑
Holzner, Steven (2006). Physics for Dummies (στα Αγγλικά). Hoboken, New Jersey: Wiley Publishing. σελίδες 201. ISBN 978-0-7645-5433-9.
angular frequency.
- ↑ Lerner, Lawrence S. (1 Ιανουαρίου 1996). Physics for scientists and engineers (στα Αγγλικά). σελ. 145. ISBN 978-0-86720-479-7.
- ↑ Mohr, J. C.; Phillips, W. D. (2015). «Dimensionless Units in the SI» (στα αγγλικά). Metrologia 52 (1): 40–47. doi:. Bibcode: 2015Metro..52...40M.
- ↑ «SI units need reform to avoid confusion» (στα αγγλικά). Nature 548 (7666): 135. 7 August 2011. doi:. PMID 28796224.
- ↑ Serway, Raymond A.· Jewett, John W. (2006). Principles of physics (στα Αγγλικά) (4th έκδοση). Belmont, CA: Brooks / Cole – Thomson Learning. σελίδες 375, 376, 385, 397. ISBN 978-0-534-46479-0.
- ↑ Nahvi, Mahmood· Edminister, Joseph (2003). Schaum's outline of theory and problems of electric circuits (στα Αγγλικά). McGraw-Hill Companies (McGraw-Hill Professional). σελίδες 214, 216. ISBN 0-07-139307-2. (LC1)
Βιβλιογραφία
[Επεξεργασία | επεξεργασία κώδικα]- Olenick, Richard P.· Apostol, Tom M. (2007). The Mechanical Universe. New York City: Cambridge University Press. σελίδες 383–385, 391–395. ISBN 978-0-521-71592-8.





















