Χρήστης:Giannislapop/πρόχειρο

Αυτή η σελίδα αφορά the function e^x. Για exponentially increasing functions of the more general form cb^x, δείτε: Exponential growth.

Η φυσική εκθετική συνάρτηση $y=e^{x}$

Στα μαθηματικά, η εκθετική συνάρτηση είναι η συνάρτηση e^x, όπου e είναι ο αριθμός (περίπου 2.718281828) έτσι ώστε η συνάρτηση e^x είναι ίση με την παράγωγό της. Η εκθετική συνάρτηση χρησιμοποιείται για να διαμορφώσει μια σχέση στην οποία μια σταθερή αλλαγή στην ανεξάρτητη μεταβλητή δίνει την ίδια ποσοστιαία μεταβολή (δηλ. ποσοστιαία αύξηση ή μείωση) στην εξαρτημένη μεταβλητή. Η συνάρτηση συχνά γράφεται ως exp ( Χ), ειδικά όταν δεν είναι πρακτικό να γραφεί η ανεξάρτητη μεταβλητή ως εκθέτης. Η εκθετική συνάρτηση χρησιμοποιείται ευρέως στη φυσική, χημεία, μηχανική, μαθηματική βιολογία, τα οικονομικά και τα μαθηματικά.

Εκθετική συνάρτηση

Τύπος	$e^{x}\,$
Αντίστροφος	$\ln x\,$
Παράγωγος	$e^{x}\,$
Αόριστο ολοκλήρωμα	$e^{x}+C\,$

Η γραφική παράσταση της y = e^x έχει θετική κλίση, κι αυξάνεται ταχύτερα καθώς το x αυξάνεται. Το γράφημα βρίσκεται πάντα πάνω από τον άξονα των x αλλά μπορεί απότομα να πλησιάσει σε αυτόν για αρνητικό x. Έτσι, ο άξονας των x είναι οριζόντια ασύμπτωτη. Η κλίση της εφαπτομένης στη γραφική παράσταση της συνάρτησης σε κάθε σημείο είναι ίση με το αντίστοιχο y σε εκείνο το σημείο. Η αντίστροφη συνάρτηση είναι ο φυσικός λογάριθμος ln(x) . Λόγω αυτού, κάποια παλιά κείμενα αναφέρονται στην εκθετική συνάρτηση ως αντιλογάριθμο.

Μερικές φορές ο όρος εκθετική συνάρτηση χρησιμοποιείται με γενικότερο τρόπο για συναρτήσεις της μορφής cb^x, όπου η βάση b είναι οποιοσδήποτε θετικός πραγματικός αριθμός, κι όχι απαραίτητα e. Δείτε την εκθετική επέκταση γι'αυτή της τη χρήση.

Γενικά, η μεταβλητή x μπορεί να είναι οποιοσδήποτε πραγματικός ή μιγαδικός αριθμός, ή ακόμα κι ένα εντελώς διαφορετικού είδους μαθηματικό αντικείμενο. Συμβουλευτείτε τον τυπικό ορισμό παρακάτω.

Γενικά

Η εκθετική συνάρτηση αυξάνεται όταν κάποια ποσότητα αυξάνεται είτε φθίνει σε βαθμό αναλογικό με την τιμή του. Μια τέτοια περίπτωση είναι ο συνεχής ανατοκισμός,και στην πραγματικότητα είναι αυτό που οδήγησε τον Jacob Bernoulli το 1683 στον αριθμό

$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

σήμερα γνωστό ως e. Αργότερα, το 1697, ο Johann Bernoulli μελέτησε το λογισμό της εκθετικής συνάρτησης.

Εάν ένα αρχικό κεφάλαιο του 1 τοκίζεται με ετήσιο ρυθμό x κάθε μήνα, τότε οι τόκοι που καταβάλλονται κάθε μήνα είναι x/12 φορές την αρχική αξία, οπότε κάθε μήνα η συνολική αξία πολλαπλασιάζεται με (1+x/12), κι η αξία στο τέλος του χρόνου είναι (1+x/12)¹². Αν από την άλλη το ποσό τοκίζεται καθημερινά τότε η τελική αξία γίνεται (1+x/365)³⁶⁵. Αφήνοντας τον αριθμό των χρονικών διαστημάτων ανά έτος να αυξάνεται χωρίς περιορισμό οδηγούμαστε στον οριακό ορισμό της εκθετικής συνάρτησης ,

$\exp(x)=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$

αρχικά διατυπωμένο από τον Euler. Αυτός είναι ένας από τους πολλούς χαρακτηρισμούς της εκθετικής συνάρτησης. Οι άλλοι αναφέρονται σε σειρές ή διαφορικές εξισώσεις.

Από οποιονδήποτε από τους ορισμούς αυτούς μπορεί να δειχθεί ότι η εκθετική συνάρτηση ακολουθεί τη βασική εκθετική ταυτότητα,

$\exp(x+y)=\exp(x)\cdot \exp(y)$

που είναι κι ο λόγος που μπορεί να γραφεί ως e^x.

Η παράγωγος (ο ρυθμός μεταβολής) της εκθετικής συνάρτησης είναι η ίδια η εκθετική συνάρτηση. Γενικότερα, μια συνάρτηση με ρυθμό μεταβολής ανάλογο με την ίδια τη συνάρτηση (κι όχι απαραίτητα ίσο με αυτή) μπορεί να εκφραστεί όπως η εκθετική συνάρτηση. Αυτή η ιδιότητα της συνάρτησης οδηγεί σε εκθετική αύξηση είτε σε εκθετική μείωση.

Η εκθετική συνάρτηση επεκτείνεται σε ένα σύνολο συναρτήσεων στο μιγαδικό επίπεδο. Ο τύπος του Euler συσχετίζει τις αξίες σε καθαρά φανταστικά επιχειρήματα για τις τριγωνομετρικές συναρτήσεις. Η εκθετική συνάρτηση έχει επίσης αναλογίες για το ποιο επιχείρημα είναι πλέγμα, ή ακόμα κι ένα στοιχείο της Άλγεβρας Banach ή και μια Άλγεβρα Lie.

Τυπικός Ορισμός

Η εκθετική συνάρτηση (με μπλε χρώμα), και το άθροισμα των πρώτων n + 1 όρων της δυναμοσειράς στα αριστερά (με κόκκινο χρώμα).

Η εκθετική συνάρτηση e^x μπορεί να χαρακτηριστεί με μια ποικιλία ισοδύναμων τρόπων. Ειδικότερα, μπορεί να οριστεί από την ακόλουθη δυναμοσειρά:

$e^{x}=\sum _{n=0}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots$

Η χρήση ενός εναλλακτικού ορισμού για την εκθετική συνάρτηση οδηγεί στο ίδιο αποτέλεσμα με την επέκτασή της ως σειρά Taylor .

Λιγότερο συχνά, η e^x ορίζεται ως η λύση y της εξίσωσης:

$x=\int _{1}^{y}{dt \over t}$

Είναι επίσης το ακόλουθο όριο:

$e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}$

Παράγωγοι και διαφορικές εξισώσεις

Η παράγωγος της εκθετικής συνάρτησης είναι ίση με την τιμή της συνάρτησης. Από κάθε σημείο $P$ της καμπύλης (μπλε), σχεδιάζεται η εφαπτομένη (κόκκινο), και μια κάθετη (πράσινο) με ύψος $h$ , σχηματίζοντας ένα τρίγωνο δεξιά με μια βάση $b$ στον άξονα $x$. Καθώς η κλίση της κόκκινης εφαπτομένης (η παράγωγος) στο $P$ είναι ίση με το λόγο του ύψους του τριγώνου προς τη βάση του τριγώνου , κι η παράγωγος είναι ίση με την τιμή της συνάρτησης, το $h$ πρέπει να είναι ίσο με το λόγο $h$ προς $b$. Έτσι η βάση $b$ πρέπει πάντα να είναι $1$.

Η σημασία της εκθετικής συνάρτησης στα μαθηματικά, και τις επιστήμες γενικότερα, πηγάζει βασικά από τις ιδιότητες της παραγώγου. Πιο συγκεκριμένα,

${\operatorname {d} \over \operatorname {d} x}e^{x}=e^{x}$

δηλαδή, η e^x είναι η ίδια η παράγωγός της και συνεπώς είναι ένα απλό παράδειγμα μιας συνάρτησης του Pfaff. Συναρτήσεις της μορφής ce^x για μια σταθερά c είναι οι μόνες συναρτήσεις με αυτήν την ιδιότητα (σύμφωνα με το Θεώρημα Picard–Lindelöf). Άλλοι τρόποι για να πούμε το ίδιο πράγμα είναι:

• Η κλίση του γραφήματος σε κάθε σημείο είναι το ύψος της συνάρτησης στο σημείο αυτό.
• Ο βαθμός αύξησης της συνάρτησης στο x είναι ίσος με την τιμή της συνάρτησης στο x.
• Η συνάρτηση λύνει τη διαφορική εξίσωση y ′ = y.
• exp is a σταθερό σημείο της παραγώγου as a functional.

Αν ο βαθμός αύξησης ή μείωσης μιας μεταβλητής είναι αναλογικός με το μέγεθός του—όπως στην περίπτωση της απεριόριστης αύξησης του πληθυσμού (δείτε Μαλθουσιανή καταστροφή),όπου συνεχώς προστίθενται τόκοι, είτε όπως στη ραδιενεργή διάσπαση, τότε η μεταβλητή μπορεί να γραφεί ως μια σταθερά επί την εκθετική συνάρτηση του χρόνου. Φυσικά για κάθε πραγματική σταθερά k, μια συνάρτηση f: R→R ικανοποιεί την f′ = kf αν και μόνον αν f(x) = ce^kx για κάποια σταθερά c.

Επιπλέον για οποιαδήποτε διαφορική εξίσωση f(x), βρίσκουμε, από τον κανόνα της αλυσίδας:

${\operatorname {d} \over \operatorname {d} x}e^{f(x)}=f'(x)e^{f(x)}$

Συνεχή κλάσματα για την e^x

Ένα συνεχές κλάσμα για την e^x μπορεί να προκύψει από μια ταυτότητα του Euler:

$e^{x}=1+{\cfrac {x}{1-{\cfrac {x}{x+2-{\cfrac {2x}{x+3-{\cfrac {3x}{x+4-{\cfrac {4x}{x+5-{\cfrac {5x}{x+6-\ddots }}}}}}}}}}}}$

Η ακόλουθη γενικευμένη συνεχής συνάρτηση για την e^z συγκλίνει γρηγορότερα:

$e^{z}=1+{\cfrac {2z}{2-z+{\cfrac {z^{2}}{6+{\cfrac {z^{2}}{10+{\cfrac {z^{2}}{14+{\cfrac {z^{2}}{18+{\cfrac {z^{2}}{22+{\cfrac {z^{2}}{26+\ddots }}}}}}}}}}}}}}$

είτε, αντικαθιστώντας με z = ^x⁄_y:

$e^{\frac {x}{y}}=1+{\cfrac {2x}{2y-x+{\cfrac {x^{2}}{6y+{\cfrac {x^{2}}{10y+{\cfrac {x^{2}}{14y+{\cfrac {x^{2}}{18y+{\cfrac {x^{2}}{22y+{\cfrac {x^{2}}{26y+\ddots }}}}}}}}}}}}}}$

Ειδική περίπτωση για z = 2:

$e^{2}=1+{\cfrac {4}{0+{\cfrac {2^{2}}{6+{\cfrac {2^{2}}{10+{\cfrac {2^{2}}{14+\ddots \,}}}}}}}}=7+{\cfrac {2}{5+{\cfrac {1}{7+{\cfrac {1}{9+{\cfrac {1}{11+\ddots \,}}}}}}}}$

Αυτός ο τύπος επίσης συγκλίνει, αν και πιο αργά, για z > 2. Για παράδειγμα:

$e^{3}=1+{\cfrac {6}{-1+{\cfrac {3^{2}}{6+{\cfrac {3^{2}}{10+{\cfrac {3^{2}}{14+\ddots \,}}}}}}}}=13+{\cfrac {54}{7+{\cfrac {9}{14+{\cfrac {9}{18+{\cfrac {9}{22+\ddots \,}}}}}}}}$

Μιγαδικό επίπεδο

Η εκθετική συνάρτηση στο μιγαδικό επίπεδο.Η μετάβαση από το σκοτεινό τμήμα στο φωτεινό υποδηλώνει ότι το εύρος της συνάρτησης αυξάνεται προς τα δεξιά. Οι περιοδικές οριζόντιες γραμμές δείχνουν ότι η εκθετική συνάρτηση είναι περιοδική συνάρτηση από φανταστικής άποψης

Όπως και στους πραγματικούς, η εκθετική συνάρτηση μπορεί να οριστεί και στο μιγαδικό επίπεδο σε διάφορες ισοδύναμες μορφές. Ένας τέτοιος ορισμός παραλληλίζει τον ορισμό δυναμοσειρών πραγματικών αριθμών, όπου η πραγματική μεταβλητή αντικαθίσταται από έναν μιγαδικό αριθμό:

$e^{z}=\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}$

Η εκθετική συνάρτηση είναι περιοδική με φανταστική περίοδο $2\pi i$ και μπορεί να γραφεί ως

$e^{a+bi}=e^{a}(\cos b+i\sin b)$

όπου a και b είναι πραγματικές τιμές και στα δεξιά οι πραγματικές συναρτήσεις πρέπει να χρησιμοποιούνται, εάν χρησιμοποιηθούν ως ορισμοί (δείτε επίσης Τύπος του Euler).Αυτός ο τύπος συνδέει την εκθετική συνάρτηση με τις τριγωνομετρικές συναρτήσεις και με τις υπερβολικές συναρτήσεις.

Όταν θεωρείται ως συνάρτηση ορισμένη στο μιγαδικό επίπεδο,η εκθετική συνάρτηση διατηρεί τις ιδιότητες:

• $e^{z+w}=e^{z}e^{w}\,$
• $e^{0}=1\,$
• $e^{z}\neq 0$
• ${\operatorname {d} \over \operatorname {d} z}e^{z}=e^{z}$
• $\,(e^{z})^{n}=e^{nz},n\in \mathbb {Z}$

για κάθε z και w.

Η εκθετική συνάρτηση είναι μια ακεραία συνάρτηση καθώς είναι ολόμορφη σε όλο το μιγαδικό επίπεδο. Δέχεται κάθε μιγαδικό αριθμό εκτός του 0. Αυτό είναι ένα παράδειγμα του μικρού θεωρήματος Picard ότι κάθε μη σταθερή ακεραία συνάρτηση δέχεται κάθε μιγαδικό αριθμό με εξαίρεση το πολύ μια τιμή.

Επεκτείνοντας το φυσικό λογάριθμο στους μιγαδικούς έχουμε τον μιγαδικό λογάριθμο log z, που είναι μια συνάρτηση πολλαπλών τιμών.

Έπειτα μπορούμε να ορίσουμε μια πιο γενική ύψωση σε δύναμη:

$z^{w}=e^{w\log z}$

για κάθε μιγαδικό z και w. Αυτή είναι επίσης συνάρτηση πολλαπλών τιμών, ακόμα κι όταν ο z είναι πραγματικός. Η διάκριση αυτή είναι προβληματική, καθώς οι συναρτήσεις πολλαπλών τιμών log z and z^w συγχέονται εύκολα με τις αντίστοιχες μονότιμες κατά την αντικατάσταση ενός πραγματικού με z. Ο κανόνας για τον πολλαπλασιασμό εκθετών στην περίπτωση θετικών πραγματικών αριθμών πρέπει να τροποποιηθεί σε ένα πλαίσιο πολλαπλών τιμών:

$(e^{z})^{w}\neq e^{zw}$, αλλά $(e^{z})^{w}=e^{(z+2\pi in)w}\,$ για πολλούς ακέραιους n

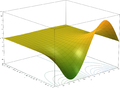
Η εκθετική συνάρτηση αντιστοιχεί κάθε ευθεία στο μιγαδικό επίπεδο σε μια λογαριθμική σπείρα στο μιγαδικό επίπεδο με κέντρο το αρχικό σημείο. Παρουσιάζονται δύο ειδικές περιπτώσεις: όταν η αρχική ευθεία είναι παράλληλη στον πραγματικό άξονα, η σπείρα που προκύπτει ποτέ δεν είναι κλείνει από μόνη της. Όταν η αρχική ευθεία είναι παράλληλη στον άξονα των φανταστικών τότε η σπείρα που προκύπτει είναι κύκλος κάποιας ακτίνας.

• Σχήματα της εκθετικής συνάρτησης στο μιγαδικό επίπεδο
• 
  z = Re(e^x+iy)
• 
  z = Im(e^x+iy)
• 
  z = e^x+iy

Υπολογισμός της a^b όπου και ο a και ο b είναι μιγαδικοί

Η μιγαδική ύψωση σε δύναμη a^b μπορεί να οριστεί αντικαθιστώντας το a με πολικές συντεταγμένες και χρησιμοποιώντας την ταυτότητα (e^ln(a))^b = a^b:

$a^{b}=\left(re^{\theta i}\right)^{b}=\left(e^{\ln(r)+\theta i}\right)^{b}=e^{(\ln(r)+\theta i)b}$

Παρολαυτά, όταν ο b δεν είναι ακέραιος, αυτή η συνάρτηση γίνεται πολλαπλών τιμών, επειδή ο θ δεν είναι μοναδικός.

Πίνακες και άλγεβρες Banach

Η δυναμοσειρά ως έκφραση της εκθετικής συνάρτησης έχει νόημα στους τετραγωνικούς πίνακες (κι έτσι η συνάρτηση παίρνει το χαρακτηρισμό εκθετικός πίνακας) και γενικότερα σε κάθε άλγεβρα Banach B. Σε αυτή την περίπτωση,η e⁰ = 1, και η e^x είναι αντιστρέψιμη, με αντίστροφο e^−x για οποιοδήποτε x στη B. Εάν xy =yx, τότε e^x+y = e^xe^y, μια ταυτότητα που δεν ισχύει για μη μετατρέψιμα x και y.

Κάποιοι εναλλακτικοί ορισμοί οδηγούν στην ίδια συνάρτηση. Για παράδειγμα, η e^x μπορεί να οριστεί ως $\textstyle \lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$

ή η e^x μπορεί να οριστεί ως f(1), όπου f: R→B είνια η λύση της διαφορικής εξίσωσης f′(t) = xf(t) με αρχική συνθήκη f(0) = 1.

Σε άλγεβρες Lie

Δωθέντος μιας ομάδα Lie G και της αντίστοιχης άλγεβρας Lie ${\mathfrak {g}}$, ο εκθετικός map είναι ένας map ${\mathfrak {g}}\to G$ που ικανοποιεί παρόμοιες προϋποθέσεις. Στην πραγματικότητα, από τη στιγμή που η R είναι η Lie άλγεβρα της ομάδας Lie όλων των θετικών πραγματικών πολλαπλασίων, η κοινή εκθετική συνάρτηση για πραγματικούς ισχυρισμούς είναι μια ιδιαίτερη περίπτωση Lie άλγεβρας. Ομοίως, καθώς η ομάδα Lie GL(n,R) των αντιστρέψιμων n × n πινάκων έχει ως Lie άλγεβρα M(n,R), το κενό όλων των n × n πινάκων, η εκθετική συνάρτηση για τετραγωνικούς πίνακες είναι μια ειδική περίπτωση της του εκθετικού !!!χάρτη Lie άλγεβρας .

Η ταυτότητα exp(x+y) = exp(x)exp(y) μπορεί να μην ισχύει για στοιχεία της Lie άλγεβρας x και y που δεν μετακινούνται. Ο τύπος των Baker–Campbell–Hausdorff παρέχει τους απαραίτητους διορθωτικούς όρους.

Διπλά εκθετική συνάρτηση

Ο όρος διπλά εκθετική συνάρτηση μπορεί να έχει δύο σημασίες:

• μια συνάρτηση με δύο εκθετικούς όρους, με διαφορετικούς εκθέτες Πρότυπο:Clarify
• μια συνάρτηση της μορφής f(x) = a^ax. Αυτή αυξάνεται γρηγορότερα από μια εκθετική συνάρτηση. Για παράδειγμα, αν a = 10 τότε : f(−1) = 1.26, f(0) = 10, f(1) = 10¹⁰, f(2) = 10¹⁰⁰ = googol, …, f(100) = googolplex.

Οι παράγωγοι αυξάνουν γρηγορότερα από τις εκθετικές συναρτήσεις , αλλά πιο αργά από τις διπλά εκθετικές συναρτήσεις. Οι αριθμοί του Φερμά, που παράγονται από την $\,F(m)=2^{2^{m}}+1$ και οι διπλοί αριθμοί του Μαρσέν που παράγονται από την $\,MM(p)=2^{2^{p}-1}-1$ είναι παραδείγματα διπλά εκθετικών συναρτήσεων.

Όμοιες ιδιότητες του e κι η συνάρτηση e^z

Η συνάρτηση e^z δεν είναι μια C(z) συνάρτηση (δηλαδή, δεν είναι πηλίκο δύο πολυωνύμων με μιγαδικούς συντελεστές) .

Για n διαφορετικούς μιγαδικούς αριθμούς {a₁, …, a_n}, το σύνολο {e^a₁z, …, e^a_nz} είναι γραμμικά ανεξάρτητο πάνω στο C(z).

Η συνάρτηση e^z είναι υπερβατική στο C(z).

Συμβουλευτείτε επίσης

• e (μαθηματική σταθερά)
• εκθετική φθορά
• χαρακτηρισμοί της εκθετικής συνάρτησης
• εκθετικό πεδίο
• εκθετική αύξηση
• ύψωση σε δύναμη
• List of exponential topics
• List of integrals of exponential functions
• p-adic exponential function
• Carlitz exponential - a characteristic p analogue
• Tetration
• Padé approximation can be used to approximate the exponential function by a fraction of polynomial functions.

Εξωτερικοί σύνδεσμοι

• Hazewinkel, Michiel, επιμ.. (2001), «Exponential function», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/e036910 
• Complex exponential function στο PlanetMath.
• Derivative of exponential function στο PlanetMath.
• Derivative of exponential function interactive graph
• Weisstein, Eric W., "Exponential Function" από το MathWorld.
• Taylor Series Expansions of Exponential Functions at efunda.com
• Complex exponential interactive graphic
• Derivative of exp(x^n) by limit definition
• General exponential limit

Category:Elementary special functions Category:Analytic functions Category:Exponentials Category:Special hypergeometric functions Category:E (mathematical constant)