Μοναδιαίος κύκλος

Κινούμενο σχέδιο που ξετυλίγει την περιφέρεια ενός μοναδιαίου κύκλου, δηλαδή ενός κύκλου με ακτίνα 1. Εφόσον $C = 2 πr$ , η περιφέρεια ενός μοναδιαίου κύκλου είναι $2π$ .

Στα μαθηματικά, ο μοναδιαίος κύκλος είναι ένας κύκλος μοναδιαίας ακτίνας - δηλαδή, έχει ακτίνα 1.^[1] Συχνά, ειδικά στην τριγωνομετρία, ο μοναδιαίος κύκλος ορίζεται να είναι ο κύκλος με ακτίνα 1 και κέντρο την αρχή (0,0) στο καρτεσιανό σύστημα συντεταγμένων πανω στο ευκλείδειο επίπεδο. Στην τοπολογία, συχνά συμβολίζεται ως $S 1$ επειδή είναι μια μονοδιάστατη $n$ -σφαίρα.^[2]

Αν $(x, y)$ είναι ένα σημείο της περιφέρειας του μοναδιαίου κύκλου, τότε $\mid x\mid$ και $\mid y\mid$ είναι τα μήκη των κάθετων πλευρών ενός ορθογωνίου τριγώνου του οποίου η υποτείνουσα έχει μήκος 1. Έτσι, σύμφωνα με το πυθαγόρειο θεώρημα, τα $x$ και $y$ ικανοποιούν την εξίσωση

x^{2}+y^{2}=1.

Εφόσον

x 2 = (- x) 2

για κάθε

x

, και εφόσον η ανάκλαση οποιουδήποτε σημείου στον μοναδιαίο κύκλο γύρω από τον άξονα

x

ή τον άξονα

y

βρίσκεται επίσης στον μοναδιαίο κύκλο, η παραπάνω εξίσωση ισχύει για όλα τα σημεία

(x, y)

του μοναδιαίου κύκλου, όχι μόνο για αυτά που ανήκουν στο πρώτο τεταρτημόριο.

Το εσωτερικό του μοναδιαίου κύκλου ονομάζεται ανοιχτός μοναδιαίος δίσκος, ενώ το εσωτερικό του μοναδιαίου κύκλου σε συνδυασμό με τον ίδιο τον κύκλο ονομάζεται κλειστός μοναδιαίος δίσκος.

Κάποιος μπορεί επίσης να χρησιμοποιήσει άλλες έννοιες της «απόστασης» για να ορίσει άλλους «μοναδιαίους κύκλους», όπως τον κύκλο του Ρίμαν.

Στο μιγαδικό επίπεδο[Επεξεργασία | επεξεργασία κώδικα]

Κινούμενο σχέδιο του μοναδιαίου κύκλου χρησιμοποιώντας γωνίες

Στο μιγαδικό επίπεδο, οι αριθμοί μοναδιαίου μέτρου ονομάζονται μοναδιαίοι μιγαδικοί αριθμοί. Αυτό είναι το σύνολο των μιγαδικών αριθμών $z$ που ικανοποιούν την εξίσωση $|z|=1.$ Όταν χωριστεί στο πραγματικό και φανταστικό μέρος το $z$ , δηλαδή $z=x+iy,$ τότε ισχύει η παρακάτω συνθήκη: $|z|^{2}=z{\bar {z}}=x^{2}+y^{2}=1.$

Ο μιγαδικός μοναδιαίος κύκλος μπορεί να παραμετροποιηθεί με μια γωνία $\theta$ που σχηματίζεται με τον θετικό πραγματικό άξονα, χρησιμοποιώντας τη μιγαδική εκθετική συνάρτηση: $z=e^{i\theta }=\cos \theta +i\sin \theta .$ (Βλέπε Τύπος του Όιλερ.)

Τριγωνομετρικές συναρτήσεις στον μοναδιαίο κύκλο[Επεξεργασία | επεξεργασία κώδικα]

Οι τριγωνομετρικές συναρτήσεις συνημίτονο και ημίτονο της γωνίας $θ$ μπορούν να οριστούν στον μοναδιαίο κύκλο ως εξής: Αν $(x, y)$ είναι ένα σημείο του μοναδιαίου κύκλου και αν η ακτίνα από την αρχή $(0, 0)$ έως το σημείο $(x, y)$ σχηματίζει μια γωνία $θ$ με τον θετικό ημιάξονα $x$ , (όπου η αριστερόστροφη κατεύθυνση είναι θετική), τότε

\cos \theta =x\quad {\text{and}}\quad \sin \theta =y.

Έτσι, η εξίσωση

x 2 + y 2 = 1

δίνει τη σχέση

\cos ^{2}\theta +\sin ^{2}\theta =1.

Ο μοναδιαίος κύκλος δείχνει επίσης ότι το ημίτονο και το συνημίτονο είναι περιοδικές συναρτήσεις, με τις ταυτότητες

\cos \theta =\cos(2\pi k+\theta )

να ισχύουν για κάθε ακέραιο

k

.

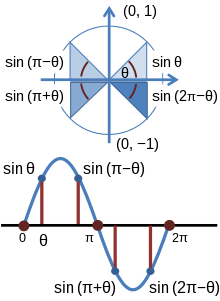
Τα τρίγωνα που κατασκευάζονται στον μοναδιαίο κύκλο μπορούν επίσης να χρησιμοποιηθούν για να απεικονίσουν την περιοδικότητα των τριγωνομετρικών συναρτήσεων. Αρχικά, κατασκευάζουμε μια ακτίνα $OP$ από την αρχή $O$ έως ένα σημείο $P(x 1, y 1)$ στον μοναδιαίο κύκλο, έτσι ώστε να σχηματίζεται με τον θετικό ημιάξονα x μια γωνία $t$ με $0 < t < π / 2$ . Στη συνέχεια, θεωρούμε το σημείο $Q(x 1,0)$ και τα ευθύγραμμα τμήματα $PQ ⊥ OQ$ . Το αποτέλεσμα είναι ένα ορθογώνιο τρίγωνο $△OPQ$ με $∠QOP = t$ . Επειδή το $PQ$ έχει μήκος $y 1$ , το $OQ$ έχει μήκος $x 1$ και το $OP$ έχει μήκος 1 ως ακτίνα του μοναδιαίου κύκλου, $sin(t) = y 1$ και $cos(t) = x 1$ . Έχοντας καθορίσει αυτές τις σχέσεις, ας πάρουμε μια άλλη ακτίνα $OR$ από την αρχή $O$ έως ένα σημείο $R(- x 1, y 1)$ στον μοναδιαίο κύκλο, έτσι ώστε να σχηματίζεται η ίδια γωνία t με τον αρνητικό ημιάξονα x. Στη συνέχεια, θεωρούμε το σημείο $S(- x 1,0)$ και τα ευθύγραμμα τμήματα $RS ⊥ OS$ . Το αποτέλεσμα είναι ένα ορθογώνιο τρίγωνο $△ORS$ με $∠SOR = t$ . Φαίνεται επομένως ότι, επειδή $∠ROQ = π - t$ , το σημείο $R$ έχει συντεταγμένες $(cos(π - t), sin(π - t))$ και το σημείο $P$ έχει συντεταγμένες $(cos(t), sin(t))$ . Το συμπέρασμα είναι ότι, εφόσον το σημείο $(- x 1, y 1)$ είναι το ίδιο με το $(cos(π - t), sin(π - t))$ και το σημείο $(x 1, y 1)$ είναι το ίδιο με το $(cos(t),sin(t))$ , ισχύει ότι $sin(t) = sin(π - t)$ και $-cos(t) = cos(π - t)$ . Μπορεί να συναχθεί με παρόμοιο τρόπο ότι $tan(π - t) = -tan(t)$ , αφού $tan(t) = y 1 / x 1$ και $tan(π - t) = y 1 / - x 1$ . Μια απλή επίδειξη των παραπάνω μπορεί να φανεί στην ισότητα $sin(π / 4) = sin(3π / 4) = 1 / \sqrt 2$ .

Όταν εργαζόμαστε με ορθογώνια τρίγωνα, το ημίτονο, το συνημίτονο και άλλες τριγωνομετρικές συναρτήσεις έχουν νόημα μόνο για γωνίες μεγαλύτερες του μηδενός και μικρότερες από $π$ /2. Ωστόσο, όταν ορίζονται με τον μοναδιαίο κύκλο, αυτές οι συναρτήσεις παράγουν τιμές για οποιοδήποτε γωνία με πραγματική τιμή – ακόμη και για γωνίες μεγαλύτερες από 2 $π$ . Για την ακρίβεια, και οι έξι γνωστές τριγωνομετρικές συναρτήσεις – ημίτονο, συνημίτονο, εφαπτομένη, συνεφαπτομένη, τέμνουσα και συντέμνουσα – μπορούν να οριστούν γεωμετρικά χρησιμοποιώντας τον μοναδιαίο κύκλο, όπως φαίνεται δεξιά.

Χρησιμοποιώντας τον μοναδιαίο κύκλο, μπορούμε από οποιαδήποτε τριγωνομετρική συνάρτηση να υπολογίσουμε εύκολα με το χέρι και γωνίες που δεν έχουμε επισημάνει χρησιμοποιώντας τους τύπους αθροίσματος και διαφοράς γωνιών.

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Βιβλιογραφικές αναφορές[Επεξεργασία | επεξεργασία κώδικα]

↑ Weisstein, Eric W. «Unit Circle». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 5 Μαΐου 2020.
↑ Weisstein, Eric W. «Hypersphere». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 6 Μαΐου 2020.

[1] Weisstein, Eric W. «Unit Circle». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 5 Μαΐου 2020.

[Unit_sphere-2] Weisstein, Eric W. «Hypersphere». mathworld.wolfram.com (στα Αγγλικά). Ανακτήθηκε στις 6 Μαΐου 2020.

[1]

[2]