Αλγόριθμος του Ευκλείδη

Στα μαθηματικά, ο αλγόριθμος του Ευκλείδη ή Ευκλείδειος αλγόριθμος είναι μια αποτελεσματική μέθοδος για τον υπολογισμό του μέγιστου κοινού διαιρέτη (ΜΚΔ) δύο ακέραιων αριθμών, είναι επίσης γνωστός ως ο μεγαλύτερος κοινός παράγοντας ή υψηλότερος κοινός παρονομαστής. Το όνομά του προέρχεται από τον Έλληνα μαθηματικό Ευκλείδη, ο οποίος τον περιγράφει στα βιβλία VII και X του βιβλίου του Στοιχεία.[1]
Στην απλούστερη μορφή του, ο αλγόριθμος του Ευκλείδη ξεκινά με ένα ζεύγος θετικών ακεραίων και σχηματίζει ένα νέο ζευγάρι που αποτελείται από το μικρότερο αριθμό και τη διαφορά μεταξύ των μεγαλύτερων και των μικρότερων αριθμών. Η διαδικασία επαναλαμβάνεται έως ότου οι αριθμοί είναι ίσοι. Αυτός ο αριθμός είναι τότε ο μέγιστος κοινός διαιρέτης του αρχικού ζεύγους.
Η παλαιότερη περιγραφή που υπάρχει για τον Ευκλείδειο αλγόριθμο είναι στα Στοιχεία του Ευκλείδη (περ. 300 π.Χ.), καθιστώντας τον ένα από τους παλαιότερους αριθμητικούς αλγορίθμους ακόμα σε κοινή χρήση. Ο αρχικός αλγόριθμος αφορούσε μόνο φυσικούς αριθμούς και γεωμετρικά μήκη (πραγματικοί αριθμοί), αλλά ο αλγόριθμος γενικεύτηκε τον 19ο αιώνα και σε άλλους τύπους αριθμών, όπως Gaussian ακέραιοι και πολυώνυμα μιας μεταβλητής. Αυτό οδήγησε στις σύγχρονες αφηρημένες αλγεβρικές έννοιες, όπως οι Ευκλείδειες δομές. Ο Ευκλείδειος αλγόριθμος έχει γενικευτεί περαιτέρω και σε άλλες μαθηματικές δομές, όπως κόμβους κύκλων nots και πολυώνυμα πολλών μεταβλητών .
Ο αλγόριθμος έχει πολλές θεωρητικές και πρακτικές εφαρμογές. Μπορεί να χρησιμοποιηθεί για να δημιουργήσει σχεδόν όλους τους πιο σημαντικούς παραδοσιακούς μουσικούς ρυθμούς που χρησιμοποιούνται σε διαφορετικούς πολιτισμούς σε όλο τον κόσμο.[2]Πρόκειται για ένα βασικό στοιχείο του RSA αλγορίθμου, μια μέθοδο κρυπτογράφησης δημόσιου κλειδιού που χρησιμοποιείται ευρέως στο ηλεκτρονικό εμπόριο. Χρησιμοποιείται για την επίλυση Διοφαντικών εξισώσεων, όπως η εξεύρεση αριθμών που ικανοποιούν πολλαπλά σχήματα με ίδιο ύψος και μέγεθος ( Κινέζικο θεώρημα υπολοίπων ) ή πολλαπλασιαστικά αντίστροφα ενός πεπερασμένου σώματος. Μπορεί επίσης να χρησιμοποιηθεί για την κατασκευή συνεχών κλασμάτων , στην αλυσίδα Sturm,μέθοδο για την εύρεση πραγματικών ριζών ενός πολυωνύμου, και σε πολλές σύγχρονες ακέραιες παραγοντοποιήσεις αλγορίθμων. Τέλος, είναι ένα βασικό εργαλείο για την απόδειξη θεωρημάτων στη σύγχρονη θεωρία αριθμών, όπως το θεώρημα των τεσσάρων τετραγώνων του Lagrange και το θεμελιώδες θεώρημα της αριθμητικής (μοναδική παραγοντοποίηση).
Εάν υλοποιηθεί με τη χρήση υπολοίπων της Ευκλείδειας διαίρεσης και όχι με αφαιρέσεις, ο αλγόριθμος του Ευκλείδη υπολογίζει το ΜΚΔ μεγάλων αριθμών αποτελεσματικά: Ποτέ δεν απαιτεί περισσότερα βήματα διαίρεσης από πέντε φορές τον αριθμό των ψηφίων (με βάση το 10) από τον μικρότερο ακέραιο. Αυτό αποδείχθηκε από τον Gabriel Lamé το 1844 και σηματοδοτεί την έναρξη της υπολογιστικής θεωρίας πολυπλοκότητας. Μέθοδοι για τη βελτίωση της απόδοσης του αλγορίθμου αναπτύχθηκαν τον 20ο αιώνα.
Ο ΜΚΔ των δύο αριθμών είναι ο μεγαλύτερος αριθμός που διαιρεί τους δύο χωρίς να αφήνει υπόλοιπο . Ο Ευκλείδειος αλγόριθμος βασίζεται στην αρχή ότι ο μέγιστος κοινός διαιρέτης των δύο αριθμών δεν αλλάζει εάν ο μικρότερος αριθμός αφαιρείται από το μεγαλύτερο αριθμό. Αν k , m και n είναι ακέραιοι, και το k είναι ένας κοινός παράγοντας των δύο ακεραίων αριθμών Α και Β , τότε Α = ΝΚ και Β = mk συνεπάγεται A − B = (n − m)k, συνεπώς, k είναι επίσης ένας κοινός παράγοντας της διαφοράς. Αυτό το k μπορεί επίσης να αντιπροσωπεύει τον μέγιστο κοινό διαιρέτη όπως αποδεικνύεται παρακάτω. Για παράδειγμα, το 21 είναι ο ΜΚΔ των 105 και 252 (252 = 12 × 21; 105 = 5 × 21). Από το 252 − 105 = (12 − 5) × 21 = 147, ο ΜΚΔ των 147 και 105 είναι επίσης 21.
Δεδομένου ότι ο μεγαλύτερος από τους δύο αριθμούς μειώνεται, επαναλαμβάνοντας τη διαδικασία, αυτή θα δίνει διαδοχικά μικρότερους αριθμούς μέχρι ένας από αυτούς να γίνει μηδέν. Όταν αυτό συμβεί, ο ΜΚΔ είναι ο μη μηδενικός αριθμός που απομένει. Αντιστρέφοντας τα βήματα του αλγόριθμου του Ευκλείδη , ο ΜΚΔ μπορεί να εκφραστεί ως το άθροισμα/γραμμικός συνδιασμός των δύο αρχικών αριθμών καθώς πολλαπλασιάζεται με ένα θετικό ή αρνητικό ακέραιο, π.χ. 21 = [5 × 105] + [(−2) × 252]. Αυτή η σημαντική ιδιότητα είναι γνωστή ως ταυτότητα του Bézout.
Ιστορικό - Μέγιστος κοινός διαιρέτης[Επεξεργασία | επεξεργασία κώδικα]
Ο Ευκλείδειος αλγόριθμος υπολογίζει το μέγιστο κοινό διαιρέτη (ΜΚΔ) δύο φυσικούς αριθμούς a και b. Ο μέγιστος κοινός διαιρέτης g είναι ο μεγαλύτερος φυσικός αριθμός που διαιρεί τόσο τόσο τον a οσο και τον b χωρίς να αφήνει υπόλοιπο. Συνώνυμα για το ΜΚΔ είναι ο μεγαλύτερος κοινός παράγοντας , ο υψηλότερος κοινός παρανομαστής , και το μεγαλύτερο κοινό μέτρο (GCM). Ο μέγιστος κοινός διαιρέτης συχνά γράφεται ως ΜΚΔ(a, b) ή, πιο απλά, όπως (a, b),[3] αν και το τελευταίο χρησιμοποιείται επίσης στη σημειογραφία για άλλες μαθηματικές έννοιες, όπως δισδιάστατα συγγραμικά διανύσματα.
Αν ΜΚΔ(a, b) = 1, τότε λέγεται ότι a και b είναι πρώτοι μεταξύ τους (ή σχετικά πρώτοι).[4] Αυτή η ιδιότητα δεν σημαίνει ότι a ή b είναι οι ίδιοι πρώτοι αριθμοί.[5] Για παράδειγμα, ούτε το 6 ούτε το 35 είναι πρώτοι αριθμοί, δεδομένου ότι και οι δύο έχουν δύο πρώτους παράγοντες: 6 = 2 × 3 και 35 = 5 × 7. Παρ 'όλα αυτά, 6 και 35 είναι πρώτοι μεταξύ τους. Δεν υπάρχει φυσικός αριθμός εκτός από το 1 που διαιρεί τους 6 και 35, δεδομένου ότι δεν έχουν κοινούς πρώτους παράγοντες.

Έστω g = ΜΚΔ(a, b). Δεδομένου ότι a και b είναι και οι δύο πολλαπλάσια του g , μπορούν να γραφτούν a = mg και b = ng, και δεν υπάρχει μεγαλύτερος αριθμός G > g για τον οποίο αυτό να ισχύει. Οι φυσικοί αριθμοί m και n πρέπει να είναι πρώτοι μεταξύ τους, δεδομένου ότι κάθε κοινός παράγοντας θα μπορούσε να υπολογιστεί από το m και το n ώστε να κάνει το g μεγαλύτερο. Έτσι, οποιοσδήποτε άλλος αριθμός c που διαιρεί και το a και b πρέπει να διαιρεί επίσης και το g . Ο μέγιστος κοινός διαιρέτης g των a και b είναι ο μοναδικός (θετικός) κοινός διαιρέτης του a και b που διαιρείται από οποιοδήποτε άλλο κοινό τους διαιρέτη c .[6]
Ο ΜΚΔ μπορεί να απεικονιστεί ως εξής.[7] Σκεφτείτε μια ορθογώνια περιοχή a επι b, και g κάθε κοινός διαιρέτης που διαιρεί ταυτόχρονα τα a και b ακριβώς. Οι πλευρές του ορθογωνίου μπορούν να διαιρεθούν σε τμήματα μήκους c , το οποίο διαιρεί το ορθογώνιο σε ένα πλέγμα από τετράγωνα με μήκος πλευράς c. Ο μέγιστος κοινός διαιρέτης g είναι η μεγαλύτερη τιμή του c για τις οποίες αυτό είναι δυνατό. Για παράδειγμα, μια 24-επί-60 ορθογώνια περιοχή μπορεί να διαιρεθεί σε ένα πλέγμα από: 1-επί-1 τετραγώνα, 2-επί-2 τετράγωνα, 3-επί-3 τετράγωνα, 4-επί-4 τετράγωνα, από 6-επί -6 τετράγωνα ή 12-από-12 τετράγωνα. Ως εκ τούτου, 12 είναι ο μέγιστος κοινός διαιρέτης του 24 και 60. Μία 24-επί-60 ορθογώνια περιοχή μπορεί να διαιρεθεί σε ένα πλέγμα 12-επί-12 τετραγώνων, με δύο τετράγωνα κατά μήκος ενός άκρου (24/12 = 2) και πέντε τετράγωνα κατά μήκος του άλλου (60/12 = 5) .
Ο ΜΚΔ δύο αριθμών a και b είναι το γινόμενο των πρώτων παραγόντων που είναι κοινοί των δύο αριθμών, όπου ένας κοινός πρώτος παράγοντας μπορεί να χρησιμοποιηθεί πολλές φορές, αλλά μόνο για όσο το γινόμενο αυτών των παραγόντων διαιρεί και το a και το b.[8] Για παράδειγμα,αφού το 1386 μπορεί να υπολογιστεί σε 2 × 3 × 3 × 7 × 11 και το 3213 μπορεί να υπολογιστεί ως 3 × 3 × 3 × 7 × 17 , ο μέγιστος κοινός διαιρέτης των 1386 και 3213 ισούται με 63 = 3 × 3 × 7 , δηλαδή το αποτέλεσμα των κοινών τους πρώτων παραγόντων. Αν δύο αριθμοί δεν έχουν κοινούς πρώτους παράγοντες,ο μέγιστος κοινός διαιρέτης τους είναι το 1 (που λαμβάνεται εδώ ως παράδειγμα για το κενό ), με άλλα λόγια, είναι πρώτοι μεταξύ τους. Ένα βασικό πλεονέκτημα του Ευκλείδειου αλγόριθμου είναι ότι μπορεί να βρει το ΜΚΔ αποτελεσματικά χωρίς να χρειάζεται να υπολογίσει τους πρώτους παράγοντες.[9][10] Η ακέραια παραγοντοποίηση μεγάλων ακεραίων πιστεύεται ότι είναι υπολογιστικά πολύ δύσκολο πρόβλημα, και η ασφάλεια πολλών σύγχρονων συστημάτων κρυπτογραφίας βασίζεται στο γεγονός ότι αυτό είναι σχεδόν ακατόρθωτο εγχείρημα.[11]
Ένας άλλος ορισμός του ΜΚΔ είναι χρήσιμος στον τομέα των προηγμένων μαθηματικών, κυρίως στη θεωρία δακτυλίων.[12] Ο μέγιστος κοινός διαιρέτης g δύο μη μηδενικών αριθμών a και b είναι επίσης ο μικρότερος θετικός ακέραιος γραμμικός τους συνδυασμός, δηλαδή, ο μικρότερος θετικός αριθμός της μορφής ua + vb , όπου υ και ν είναι ακέραιοι. Το σύνολο όλων των ακέραιων γραμμικών συνδυασμών των a και b είναι στην πραγματικότητα το ίδιο με το σύνολο όλων των πολλαπλάσιων του g ( mg , όπου m είναι ένας ακέραιος αριθμός). Στη σύγχρονη μαθηματική γλώσσα, το ιδανικό που παράγεται από το a και το b είναι το ιδανικό που δημιουργείται από το g μόνο (ένα ιδανικό που παράγεται από ένα μόνο στοιχείο ονομάζεται κύριο ιδανικό , και όλα τα ιδανικά των ακεραίων είναι τα κύρια ιδανικά). Μερικές ιδιότητες του ΜΚΔ είναι στην πραγματικότητα πιο εύκολο να γίνουν αντιληπτές με αυτή την περιγραφή, για παράδειγμα, το γεγονός ότι κάθε κοινός διαιρέτης του a και β διαιρεί επίσης τον ΜΚΔ τους (ο οποίος διαιρεί και τους δύο όρους της ua + vb .Η ισοδυναμία αυτού του ορισμού του ΜΔΚ με τους άλλους ορισμούς περιγράφεται κατωτέρω.
Ο ΜΚΔ τριών ή περισσότερων αριθμών ισούται με το γινόμενο των πρώτων κοινών παραγόντων όλων των αριθμών,[13] αλλά μπορεί επίσης να υπολογιστεί παίρνοντας διαδοχικά τον μέγιστο κοινό διαιρέτη ζευγών των αριθμών.[14] Για παράδειγμα,
- ΜΚΔ(a, b, c) = ΜΚΔ(a, ΜΚΔ(b, c)) = ΜΚΔ(ΜΚΔ(a, b), c) = ΜΚΔ(ΜΚΔ(a, c), b).
Έτσι, ο αλγόριθμος του Ευκλείδη, ο οποίος υπολογίζει το ΜΚΔ δύο ακεραίων χρησιμοποιείται επίσης για τον υπολογισμό του ΜΚΔ αυθαίρετα πολλών ακεραίων.
Περιγραφή[Επεξεργασία | επεξεργασία κώδικα]
Η απλούστερη μορφή του αλγορίθμου του Ευκλείδη ξεκινά με ένα ζεύγος θετικών ακεραίων και σχηματίζει ένα νέο ζευγάρι που αποτελείται από το μικρότερο αριθμό και τη διαφορά μεταξύ των μεγαλύτερων και των μικρότερων αριθμών. Η διαδικασία επαναλαμβάνεται έως ότου οι αριθμοί είναι ίσοι. Στη συνέχεια ο αριθμός αυτός είναι ο μέγιστος κοινός διαιρέτης του αρχικού ζεύγους. Ωστόσο, εάν ένας αριθμός είναι πολύ μικρότερος από τον άλλο, πολλά βήματα αφαίρεσης θα είναι αναγκαία πριν ο μεγαλύτερος αριθμός μειωθεί σε μία τιμή μικρότερη ή ίση από τον άλλον αριθμό στο ζεύγος. Αφαιρώντας ένα μικρό θετικό αριθμό από ένα μεγάλο αριθμό αρκετές φορές μέχρι αυτό που απομένει είναι μικρότερο από τον αρχικό ελάχιστο αριθμό, μπορεί να αντικατασταθεί με την εύρεση του υπόλοιπο σε μεγάλη διαίρεση. Έτσι, η μορφή διαίρεσης του αλγορίθμου του Ευκλείδη ξεκινά με ένα ζεύγος θετικών ακεραίων και σχηματίζει ένα νέο ζεύγος που αποτελείται από το μικρότερο αριθμό και το υπόλοιπο που λαμβάνεται διαιρώντας τον μεγαλύτερο αριθμό από το μικρότερο αριθμό. Η διαδικασία επαναλαμβάνεται έως ότου ένας αριθμός είναι μηδέν. Ο άλλος αριθμός είναι τότε ο μέγιστος κοινός διαιρέτης του αρχικούζεύγους.
Διαδικασία[Επεξεργασία | επεξεργασία κώδικα]
Ο Ευκλείδειος αλγόριθμος προχωρεί σε μια σειρά από βήματα έτσι ώστε το αποτέλεσμα από κάθε βήμα να χρησιμοποιείται ως δεδομένο για το επόμενο βήμα. Ας είναι k ένας ακέραιος που μετράει τα βήματα του αλγορίθμου, ξεκινώντας από το μηδέν. Ετσι, το αρχικό στάδιο αντιστοιχεί σε k = 0 , το επόμενο βήμα αντιστοιχεί στο k = 1 , και ούτω καθεξής. Κάθε βήμα ξεκινά με δύο μη αρνητικά υπόλοιπα rk−1 rk−2. Δεδομένου ότι ο αλγόριθμος εξασφαλίζει ότι τα υπόλοιπα μειώνονται σταδιακά σε κάθε βήμα, το rk−1 είναι μικρότερο από το προηγούμενο του rk−2 . Ο στόχος στο k βήμα είναι να βρεθεί είναι πηλίκο qk και το υπόλοιπο rk έτσι ώστε η εξίσωση να ικανοποιείται
- rk−2 = qk rk−1 + rk
όπου rk < rk−1 . Με άλλα λόγια, τα πολλαπλάσια του μικρότερου αριθμού rk−1 αφαιρούνται από το μεγαλύτερο αριθμό rk−2 έως ότου το υπόλοιπο είναι μικρότερο από το rk−1 . Στο αρχικό στάδιο (k = 0), τα υπόλοιπα r−2 και r−1 αντιστοιχούν στα a και b, οι αριθμοί για τους οποίους ζητείται ο ΜΚΔ. Στο επόμενο βήμα (k = 1), τα υπόλοιπα αντιστοιχούν στο b και το υπόλοιπο r0 του αρχικού βήματος, και ούτω καθεξής. Έτσι, ο αλγόριθμος μπορεί να γραφτεί ως μια ακολουθία των εξισώσεων:
- a = q0 b + r0
- b = q1 r0 + r1
- r0 = q2 r1 + r2
- r1 = q3 r2 + r3
- …
Εάν a είναι μικρότερο από το b , στο πρώτο βήμα του αλγορίθμου εναλάσσονται οι αριθμοί. Για παράδειγμα, εάν a < b , το αρχικό πηλίκο q0 ισούται με μηδέν, και το υπόλοιπο r0 είναι a . Έτσι, το rk είναι μικρότερο από το προηγούμενο του r rk−1 για όλα τα k ≥ 0.
Δεδομένου ότι τα υπόλοιπα μειώνονται σε κάθε βήμα, αλλά ποτέ δεν μπορούν να γίνουν αρνητικά, ένα υπόλοιπο rN , τελικά θα γίνει ίσο με μηδέν, όπου και ο αλγόριθμος σταματά.[15] Το τελευταίο μη μηδενικό υπόλοιπο rN−1 είναι ο μέγιστος κοινός διαιρέτης των "a" και "b" . Ο αριθμός "Ν" δεν μπορεί να είναι άπειρο, επειδή υπάρχουν μόνο πεπερασμένοι το πλήθος αριθμοί των μη αρνητικών ακέραιων ανάμεσα στο αρχικό υπολοίπο r0 και το μηδέν.
Απόδειξη της ισχύος[Επεξεργασία | επεξεργασία κώδικα]
Η ισχύς του Ευκλείδειου αλγορίθμου μπορεί να αποδειχθεί από ένα εγχείρημα δύο σταδίων.[16] Στο πρώτο στάδιο, το τελευταίο μη μηδενικό υπόλοιπο rN−1 φαίνεται να διαιρεί τόσο το a και το b . Δεδομένου ότι είναι ένας κοινός διαιρέτης, πρέπει να είναι μικρότερος ή ίσο με τον μέγιστο κοινό διαιρέτη g . Στο δεύτερο στάδιο, φαίνεται ότι κάθε κοινός διαιρέτης των a και b , συμπεριλαμβανομένου του g , πρέπει να διαιρεί το rN−1. Συνεπώς, το g πρέπει να είναι μικρότερο ή ίσο του rN−1. Αυτά τα δύο συμπεράσματα είναι ασυμβίβαστα εκτός αν rN−1 = g.
Για να δείξουμε ότι rN−1 διαιρεί τους a και b (στο πρώτο βήμα),το rN−1 διαιρεί το προηγούμενο του rN−2
- rN−2 = qN rN−1
δεδομένου ότι το τελικό υπόλοιπο rN είναι μηδέν. Το rN−1 διαιρεί επίσης και το προπροηγούμενο του rN−3
- rN−3 = qN−1 rN−2 + rN−1
γιατί διαιρεί και τους δύο όρους από τη δεξιά πλευρά της εξίσωσης. Επαναλαμβάνοντας το ίδιο επιχείρημα, το rN−1 διαιρεί όλα τα προηγούμενα υπόλοιπα, συμπεριλαμβανομένων του a και του b . Κανένα από τα προηγούμενα υπόλοιπα rN−2 , rN−3, κλπ. δε διαιρεί το a και b , εφόσον αφήνουν υπόλοιπο. Εφόσον το rN−1 είναι κοινός διαιρέτης των a και b , rN−1 ≤ g .
Στο δεύτερο στάδιο, κάθε φυσικός αριθμός c, που διαιρεί και το a και το b(με άλλα λόγια, κάθε κοινός διαιρέτης του a και b ) διαιρεί και τα υπόλοιπα rk. Εξ ορισμού, a και b μπορούν να γραφούν ως πολλαπλάσια του c: a = mc και b = nc , όπου m και n είναι φυσικοί αριθμοί. Ως εκ τούτου, c διαιρεί το αρχικό υπόλοιπο r0, δεδομένου ότι r0 = a − q0b = mc − q0nc = (m − q0n)c . Ένα ανάλογο επιχείρημα δείχνει ότι c διαιρεί επίσης, τα ακόλουθα υπόλοιπα r1, r2 κλπ. Ως εκ τούτου, ο μέγιστος κοινός διαιρέτης g πρέπει να διαιρεί rN−1 , πράγμα που σημαίνει ότιg ≤ rN−1 . Δεδομένου ότι το πρώτο μέρος του επιχειρήματος έδειξε το αντίθετο (rN−1 ≤ g), προκύπτει ότι g = rN−1 . Ετσι, είναι ο g είναι ο μεγαλύτερος κοινός διαιρέτης όλων των επόμενων ζευγών:[17] [18]
- g = GCD(a, b) = GCD(b, r0) = GCD(r0, r1) = … = GCD(rN−2, rN−1) = rN−1.
Παραδειγμα εργασίας[Επεξεργασία | επεξεργασία κώδικα]

Για παράδειγμα, ο Ευκλείδειος αλγόριθμος μπορεί να χρησιμοποιηθεί για να βρεθεί ο μέγιστος κοινός διαιρέτης a = 1071 και b = 462 .Ξεκινώντας ,πολλαπλάσια του 462 αφαιρούνται από το 1071 μέχρι το υπόλοιπο να γίνει μικρότερο από 462. Δύο τέτοια πολλαπλάσια μπορούν να αφαιρούνται (q0 = 2), αφήνοντας ένα υπόλοιπο του 147.
- 1071 = 2 × 462 + 147.
Στη συνέχεια,πολλαπλάσια του 147 αφαιρούνται από το 462 μέχρι το υπόλοιπο είναι μικρότερο από 147. τρια πολλαπλάσια μπορούν να αφαιρεθούν (q1 = 3), αφήνοντας ένα υπόλοιπο του 21.
- 462 = 3 × 147 + 21.
Στη συνέχεια,πολλαπλάσια του 21 αφαιρούνται από το 147 έως το υπόλοιπο είναι μικρότερο από 21. Επτά πολλαπλάσια μπορούν να αφαιρεθούν (q2 = 7), χωρίς να αφήσουν κανένα υπόλοιπο
- 147 = 7 × 21 + 0.
Δεδομένου ότι το τελευταίο υπόλοιπο είναι μηδέν, ο αλγόριθμος τελειώνει με 21 ως το μέγιστο κοινό διαιρέτη των 1071 και 462. Αυτό συμφωνεί με τον ΜΚΔ(1071, 462) που βρέθηκε από την παραγοντοποίηση παραπάνω . Σε μορφή πίνακα, είναι τα βήματα
| Βήμα k | Εξίσωση | Πηλίκο και υπόλοιπο |
|---|---|---|
| 0 | 1071 = q0 462 + r0 | q0 = 2 και r0 = 147 |
| 1 | 462 = q1 147 + r1 | q1 = 3 και r1 = 21 |
| 2 | 147 = q2 21 + r2 | q2 = 7 και r2 = 0 ,ο αλγόριθμος τελειώνει |
Πραγματοποίηση[Επεξεργασία | επεξεργασία κώδικα]
Ο Ευκλείδειος αλγόριθμος μπορεί να γίνει αντιληπτός στα πλάισια της αναλογίας που περιγράφεται παραπάνω για τον μέγιστο κοινό διαιρέτη.[19]Ας υποθέσουμε ότι θέλουμε να καλύψουμε ένα α-επί- b ορθογώνιο με τετράγωνα πλακάκια ακριβώς, όπου α είναι ο μεγαλύτερος από τους δύο αριθμούς . Αρχικά προσπαθούμε να καλύψουμε το ορθογώνιο με b -by- b τετράγωνα πλακάκια. ωστόσο, αυτό αφήνει ένα r0-by-bορθογώνιο ακάλυπτο, όπου r0 < b. Στη συνέχεια προσπαθούμε να καλύψουμε το υπόλοιπο ορθογώνιο με r0-by-r0 τετράγωνα πλακάκια. Αυτό αφήνει ένα δδεύτερο ακάλυπτο ορθογώνιο r1-by-r0,το οποίο προσπαθούμε να καλυψουμε με τετράγωνα πλακάκια χρησιμοποιώντας r1-by-r1 και ούτω καθεξής. Η διαδικασία τελειώνει όταν δεν υπάρχει ακάλυπτο ορθογώνιο, δηλαδή, όταν τα τετράγωνα πλακίδια καλύψουν ακριβώς, το ορθογώνιο που απέμεινε από το προηγούμενο βήμα. Το μήκος των πλευρών του μικρότερου τετράγωνου πλακιδίου είναι ο ΜΚΔ των διαστάσεων του αρχικού ορθογωνίου. Για παράδειγμα, το μικρότερο τετραγωνικό πλακίδιο στο παρακείμενο σχήμα είναι 21-επί-21 (φαίνεται σε κόκκινο), και το 21 είναι ο ΜΚΔ των 1071 και 462, οι διαστάσεις του αρχικού ορθογωνίου (που φαίνεται στο πράσινο).
Ευκλείδεια διαίρεση[Επεξεργασία | επεξεργασία κώδικα]
Σε κάθε βήμα k, ο Ευκλείδειος αλγόριθμος υπολογίζει το πηλίκο qk και το υπόλοιπο rk από δύο αριθμούς rk−1 and rk−2
- rk−2 = qk rk−1 + rk
όπου η δύναμη του rk είναι αυστηρά μικρότερη από εκείνη του rk−1. Το θεώρημα που διέπει τον ορισμό της Ευκλείδειας διαίρεσης εξασφαλίζει ότι ένα τέτοιο πηλίκο και υπόλοιπο πάντα υπάρχουν και είναι μοναδικά.[20]
Στην αρχική έκδοση του αλγορίθμου του Ευκλείδη, το πηλίκο και το υπόλοιπο βρίσκονται από επανειλημμένη αφαίρεση, Δηλαδή, rk−1 αφαιρείται από rk−2 επανειλημμένα έως ότου το υπόλοιπο rk είναι μικρότερο από rk−1. Μετά από αυτό rk και rk−1 ανταλλάσσονται και η διαδικασία επαναλαμβάνεται.Η ευκλείδεια διαίρεση μειώνει όλα τα βήματα μεταξύ δύο ανταλλαγών σε ένα ενιαίο βήμα, το οποίο είναι κατά συνέπεια πιο αποτελεσματικό. Επιπλέον, δεν είναι το πηλίκο που απαιτείται, έτσι μπορεί κανείς να αντικαταστήσει την Ευκλείδεια διαίρεση με τη modulo αριθμητική, η οποία δίνει μόνο το υπόλοιπο. Έτσι, η επανάληψη του Ευκλείδειου αλγορίθμου γίνεται απλά
- rk = rk−2 mod rk−1.
Υλοποιήσεις[Επεξεργασία | επεξεργασία κώδικα]
Υλοποιήσεις του αλγορίθμου μπορεί να εκφραστούν σε ψευδοκώδικα.Για παράδειγμα,η μέθοδος που στηρίζεται σε διαιρέσεις μπορεί να προγραμματιστεί ως [21]
function gcd(a, b)
while b ≠ 0
t := b
b := a mod t
a := t
return a
Στην αρχή της k επανάληψης, η μεταβλητή Β κατέχει το τελευταίο υπόλοιπο rk−1, ενώ η μεταβλητή a κατέχει το προηγούμενό του, rk−2. Το στάδιο b := a mod b είναι ισοδύναμο με τον ανωτέρω τύπο αναδρομής rk ≡ rk−2 mod rk−1. Η ψευδομεταβλητή t κρατά την τιμή της rk−1, ενώ το επόμενο υπόλοιπο rk υπολογίζεται συγχρόνως. Στο τέλος του βρόχου επανάληψης, η μεταβλητή b κατέχει το υπόλοιπο rk , ενώ η μεταβλητή a κατέχει το προηγούμενό του , rk−1.
Στην μέθοδο που βασίζεται στην αφαίρεση, που ήταν και η αρχική έκδοση του αλγορίθμου του Ευκλείδη, ο υπολογισμός του υπόλοιπου (b = a mod b) αντικαθίσταται από την επανειλημμένη αφαίρεση.[22] Αντίθετα με την βασισμένη στη διαίρεση έκδοση, η οποία λειτουργεί με αυθαίρετους ακέραιους ως πρωταρχικό δεδομένο, η βασισμένη στην αφαίρεση έκδοση υποθέτει ότι η είσοδος αποτελείται από θετικούς ακέραιους και σταματά όταν a = b:
function gcd(a, b)
while a ≠ b
if a > b
a := a − b
else
b := b − a
return a
Οι μεταβλητές a και b εναλλάσονται διατηρώντας τα προηγούμενα υπόλοιπα rk−1 και rk−2. Υποθέτοντας ότι a είναι μεγαλύτερο από b στην αρχή μιας επανάληψης, τότε a ισούται με rk−2, εφόσον rk−2 > rk−1. Κατά τη διάρκεια της επανάληψη του βρόχου, το a μειώνεται κατά πολλαπλάσια του προηγούμενου υπολοίπου b έως ότου a είναι μικρότερο από το b. Τότε το a είναι το επόμενο υπόλοιπο rk. Τότε το b μειώνεται κατά πολλαπλάσια του a έως ότου είναι πάλι μικρότερο από a, δίνοντας το επόμενο υπόλοιπο rk+1, και ούτω καθεξής.
Η αναδρομική έκδοση[23] βασίζεται στην ισότητα των ΜΚΔ των διαδοχικών υπολοίπων και τη συνθήκη τερματισμού ΜΚΔ(rN−1, 0) = rN−1.
function gcd(a, b)
if b = 0
return a
else
return gcd(b, a mod b)
Για παράδειγμα, ο ΜΚΔ(1071, 462) υπολογίζεται από τον αντίστοιχο ΜΚΔ(462, 1071 mod 462) = ΜΚΔ(462, 147) Ο τελευταίος ΜΚΔ υπολογίζεται από τον ΜΚΔ(147, 462 mod 147) = ΜΚΔ(147, 21) ο οποίος με τη σειρά του υπολογίζεται από τον ΜΚΔ (21, 147 mod 21) = ΜΚΔ (21, 0) = 21.
Μέθοδος των μικρότερων απόλυτων υπολοίπων[Επεξεργασία | επεξεργασία κώδικα]
Σε μια άλλη εκδοχή του αλγορίθμου του Ευκλείδη, το πηλίκο σε κάθε βήμα αυξάνεται κατά ένα, αν το προκύπτον αρνητικό υπόλοιπο είναι μικρότερο σε μέγεθος από το τυπικό θετικό υπόλοιπο.[24][25] Προηγουμένως, η εξίσωση
- rk−2 = qk rk−1 + rk
με την υπόθεση ότι |rk−1| > rk > 0. Ωστόσο, ένα εναλλακτικό αρνητικό υπόλοιπο ek μπορεί να υπολογιστεί:
- rk−2 = (qk + 1) rk−1 + ek
αν rk−1 > 0 ή
- rk−2 = (qk − 1) rk−1 + ek
αν rk−1 < 0.
Αν |ek| < |rk|, τότε rk αντικαθίσταται από το ek. Ως |rk−1| = rk − ek, αυτό το νέο rk ικανοποιεί
- |rk| < |rk−1| / 2.
Ο Leopold Kronecker έχει δείξει ότι αυτή η έκδοση απαιτεί το μικρότερο αριθμό των βημάτων οποιασδήποτε έκδοσης του αλγορίθμου του Ευκλείδη.[24][25]
Ιστορική εξέλιξη[Επεξεργασία | επεξεργασία κώδικα]

Ο Ευκλείδειος αλγόριθμος είναι ένας από τους παλαιότερους αλγορίθμους ακόμα σε κοινή χρήση.[26] Φαίνεται στα Στοιχεία του Ευκλείδη (περ. 300 π.Χ.), και συγκεκριμένα στο βιβλίο 7 (Προτάσεις 1-2) και βιβλίο 10 (Προτάσεις 2-3). Στο βιβλίο 7, ο αλγόριθμος είναι σχεδιασμένος για ακέραιους, ενώ στο βιβλίο 10, δεν έχει διατυπωθεί για μήκη τμημάτων γραμμής. (Στη σύγχρονη χρήση, θα έλεγε κανείς ότι διατυπώθηκε εκεί για πραγματικούς αριθμούς. Όμως, μήκη, εμδαδά, και όγκοι,που αντιμετωπίστηκαν ως πραγματικοί αριθμοί στη σύγχρονη χρήση, δεν μετρούνται στις ίδιες μονάδες και δεν υπάρχει καμία φυσική μονάδα μήκους, εμβαδού, ή ο όγκου, ενώ η έννοια των πραγματικών αριθμών ήταν άγνωστη εκείνη την εποχή.) Ο τελευταίος αλγόριθμος είναι γεωμετρικός. Ο ΜΚΔ των δύο μηκών α και β αντιστοιχεί στο μέγιστο μήκος γ που μετρά το α και β ομοιόμορφα, με άλλα λόγια, τα μήκη α και β είναι και τα δύο ακέραια πολλαπλάσια του μήκους g..
Ο αλγόριθμος μάλλον δεν ανακαλύφθηκε από τον Ευκλείδη, που συγκέντρωσε τα αποτελέσματα από προηγούμενους μαθηματικούς στο έργο του Στοιχεία.[27][28] Ο μαθηματικός και ιστορικός BL van der Waerden ισχυρίζεται ότι το Βιβλίο 7 προέρχεται από ένα βιβλίο σχετικά με τη θεωρία αριθμών που γράφτηκε από μαθηματικούς στη σχολή του Πυθαγόρα.[29] Ο αλγόριθμος ήταν πιθανώς γνωστός από τον Εύδοξο της Κνίδου (περίπου 375 π.Χ.).[26][30] Ο αλγόριθμος μπορεί ακόμη και να είναι προγενέστερος από τον Εύδοξο,[31][32] αν κρίνουμε από τη χρήση του τεχνικού όρου ἀνθυφαίρεσις (αμοιβαία αφαίρεση) στα έργα του Ευκλείδη και του Αριστοτέλη.[33]
Αιώνες αργότερα, ο αλγόριθμος του Ευκλείδη ανακαλύφθηκε ανεξάρτητα τόσο στην Ινδία όσο και στην Κίνα,[34] κυρίως για την επίλυση διοφαντικών εξισώσεων που προκύπτουν στην αστρονομία και την δημιουργία ακριβών ημερολογίων. Στα τέλη του 5ου αιώνα, ο Ινδός μαθηματικός και αστρονόμος Αριαμπάτα περιέγραψε τον αλγόριθμο ως «κονιοποιητή»,[35] ίσως λόγω της αποτελεσματικότητάς του στην επίλυση διοφαντικών εξισώσεων .[36] Παρά το γεγονός ότι μια ειδική περίπτωση του Κινέζικου θεωρήματος των υπολοίπων είχε ήδη περιγραφεί από τον Κινέζο μαθηματικό και αστρονόμο Sun Tzu,[37] η γενική λύση δόθηκε στη δημοσιότητα από τον Qin Jiushao το 1247 στο βιβλίο του Shushu Jiuzhang (數書九章 Mathematical Treatise in Nine Sections).[38] Ο Ευκλείδειος αλγόριθμος περιγράφηκε για πρώτη φορά στην Ευρώπη στη δεύτερη έκδοση του Bachet's Problèmes plaisants et délectables (Ευχάριστα και απολαυστικά προβλήματα, 1624) [35] Στην Ευρώπη, επίσης χρησιμοποιήθηκε για την επίλυση διοφαντικών εξισώσεων και στην ανάπτυξη συνεχών κλασμάτων. Ο γενικευμένος Ευκλείδειος αλγόριθμος, δόθηκε στη δημοσιότητα από τον Άγγλο μαθηματικό Nicholas Saunderson, ο οποίος τον απέδωσε στον Roger Cotes ως αποτελεσματική μέθοδο για τον υπολογισμό συνεχών κλασμάτων.[39]
Τον 19ο αιώνα, ο Ευκλείδειος αλγόριθμος οδήγησε στην ανάπτυξη των νέων συστημάτων αριθμών, όπως οι Gaussian ακέραιοι και οι ακέραιοι του Eisenstein . Το 1815, ο Carl Gauss χρησιμοποίησε τον Ευκλείδειο αλγόριθμο για να αποδείξει τη μοναδική παραγοντοποίηση των Gaussian ακεραίων, μολονότι το έργο του εκδόθηκε για πρώτη φορά το 1832.[40] Ο Gauss ανάφερε τον αλγόριθμο του στο Disquisitiones Arithmeticae (δημοσιεύθηκε 1801), αλλά μόνο ως μια μέθοδο για συνεχή κλάσματα.[34] Ο Peter Gustav Lejeune Dirichlet φαίνεται να ήταν ο πρώτος που περιέγραψε την Ευκλείδειο αλγόριθμο ως βάση για ένα μεγάλο μέρος της θεωρίας αριθμών.[41]Ο Lejeune Dirichlet τόνισε ότι πολλά αποτελέσματα της θεωρίας αριθμών, όπως η μοναδική παραγοντοποίηση, θα ίσχυαν και για οποιοδήποτε άλλο σύστημα των αριθμών στους οποίους ο Ευκλείδειος αλγόριθμος θα μπορούσε να εφαρμοστεί.[42]Οι διαλέξεις του Lejeune Dirichlet για τη θεωρία αριθμών επεξεργάστηκαν και επεκτάθηκαν από τον Richard Dedekind , ο οποίος χρησιμοποίησε τον αλγόριθμο του Ευκλείδη για τη μελέτη των αλγεβρικών ακέραιων , ένα νέο γενικό τύπο αριθμών. Για παράδειγμα, Dedekind ήταν ο πρώτος που απέδειξε το θεώρημα του fermat για το άθροισμα των τετραγώνων δύο αριθμών χρησιμοποιώντας τη μοναδική παραγοντοποίηση των Gaussian ακέραιων.[43] Ο Dedekind επίσης όρισε την έννοια της Ευκλείδειας δομής, ένα σύστημα αριθμών στο οποίο μια γενικευμένη εκδοχή του Ευκλείδειου αλγόριθμου μπορεί να οριστεί (όπως περιγράφεται κατωτέρω ευκλείδεις δομές). Στις τελευταίες δεκαετίες του 19ου αιώνα, ωστόσο, ο Ευκλείδειος αλγόριθμος σταδιακά υποκαταστάθηκε από την πιο γενική θεωρία του Dedekind των ιδανικών (θεωρία δακτυλίων).[44]
Άλλες εφαρμογές του αλγορίθμου του Ευκλείδη αναπτύχθηκαν τον 19ο αιώνα. Το 1829,ο Charles Sturm έδειξε ότι ο αλγόριθμος ήταν χρήσιμος στη μέθοδο Sturm chain για την εύρεση των πραγματικών ριζών των πολυωνύμων σε οποιοδήποτε διάστημα.[45]
Ο Ευκλείδιος αλγόριθμος ήταν ο πρώτος ακέραιος αλγόριθμος , ο οποίος είναι μια μέθοδος για την εύρεση ακέραιων σχέσεων μεταξύ ανάλογων πραγματικών αριθμών. Αρκετοί νέοι ακέραιοι αλγόριθμοι έχουν αναπτυχθεί τα τελευταία χρόνια, όπως ο αλγόριθμος Ferguson–Forcade (1979) του Helaman Ferguson και RW Forcade,[46] και οι παρεμφερείς του,ο δια βίου μάθησης αλγόριθμος,ο HJLS αλγόριθμος , και ο αλγόριθμος PSLQ.[47][48]
Το 1969,οι Cole και Davie ανέπτυξαν ένα παιχνίδι δύο παικτών που βασίζεται στον Ευκλείδειο αλγόριθμο, που ονομάζεται The Game of Euclid[49] το οποίο έχει μια βέλτιστη στρατηγική.[50] Οι παίκτες ξεκινούν με δύο σωρούς από α και β πέτρες. Οι παίκτες αναλαμβάνουν εκ περιτροπής την αφαίρεση m πολλαπλασίων του μικρότερου σωρού από το μεγαλύτερο. Ετσι, αν οι δύο σωροί αποτελούνται από χ και y πέτρες, όπου το Χ είναι μεγαλύτερο από το y , ο επόμενος παίκτης μπορεί να ελαττώσει το μεγαλύτερο σωρό από x πέτρες σε x − my πέτρες, εφ' όσον ο τελευταίος είναι ένας μη αρνητικός ακέραιος αριθμός. Ο νικητής είναι ο πρώτος παίκτης που θα έχει ένα σωρό από μηδέν πέτρες.[51][52]
Μαθηματικές εφαρμογές[Επεξεργασία | επεξεργασία κώδικα]
Ταυτότητα Bézout[Επεξεργασία | επεξεργασία κώδικα]
Η ταυτότητα του Bézout δηλώνει ότι ο μεγιστος κοινός διαιρέτης g δύο ακεραίων a και b μπορεί να παρασταθεί ως ένα γραμμικό άθροισμα των δύο αρχικών αριθμών a και b .[53]Με άλλα λόγια, είναι πάντα δυνατό να βρεθούν ακέραιοι s και t τέτοιοι ώστε . g = sa + tb.[54][55]
Οι ακέραιοι s και t μπορούν να υπολογιστούν από τα πηλίκα q0, q1, κλπ. αντιστρέφοντας τη σειρά των εξισώσεων στον αλγόριθμο του Ευκλείδη.[56] Αρχίζοντας με την "επόμενη προς τα τελευταία εξίσωση",το g μπορεί να εκφραστεί συναρτήσει του πηλίκου qN−1 και των δύο προηγούμενων υπολοίπων, rN−2 and rN−3. .
- g = rN−1 = rN−3 − qN−1 rN−2
Τα δύο αυτά υπόλοιπα μπορούν ομοίως να εκφράζονται συναρτήσει των πηλίκων τους και των προηγούμενων υπολοίπων τους
- rN−2 = rN−4 − qN−2 rN−3
- rN−3 = rN−5 − qN−3 rN−4.
Αντικαθιστώντας αυτές τις φόρμουλες για rN−2 και rN−3 στην πρώτη εξίσωση εκφράζουν το g ως γραμμικό άθροισμα των υπολοίπων rN−4 and rN−5 . Η διαδικασία της αντικατάστασης υπολοίπων από τους τύπους που περιλαμβάνουν τα προηγούμενα τους υπόλοιπα μπορεί να συνεχίζεται έως ότου οι αρχικοί αριθμοί α και β καταλήγουν να είναι:
- r2 = r0 − q2 r1
- r1 = b − q1 r0
- r0 = a − q0 b.
Αφού όλα τα υπολοιπα έχουν r0, r1,, κλπ. έχουν υποκατασταθεί, η τελική εξίσωση εκφράζει το g ως ένα γραμμικό άθροισμα των Α και Β :g = sa + tb.Η ταυτότητα του bezout , και ως εκ τούτου προηγούμενος αλγόριθμος, μπορεί να γενιεκυτεί και στις ευκλείδειες δομές.
Πρωταρχικά ιδανικά και συναφή προβλήματα[Επεξεργασία | επεξεργασία κώδικα]
Η ταυτότητα Bézout παρέχει ακόμη τον ορισμό του μέγιστου κοινού διαιρέτη g δύο αριθμών a και b .[12] Ας εξετάσουμε το σύνολο όλων των αριθμών ua + vb, όπου u και v είναι δύο οποιοιδήποτε ακέραιοι. Δεδομένου ότι και ο a και ο b διαιρούνται από τον g, κάθε αριθμός του συνόλου είναι διαιρετός από τον g. Με άλλα λόγια, κάθε αριθμός του συνόλου είναι ένα ακέραιο πολλαπλάσιο του g. Αυτό ισχύει για κάθε κοινό διαιρέτη του a και b. Ωστόσο, σε αντίθεση με άλλους κοινούς διαιρέτες, ο μέγιστος κοινός διαιρέτης είναι ένα μέλος του συνόλου. Με την ταυτότητα του Bézout, επιλέγονταςu = s καιv = t παίρονουμε τον g. Ένας μικρότερος κοινός διαιρέτης δεν μπορεί να είναι μέλος του συνόλου, αφού κάθε μέλος του συνόλου πρέπει να διαιρείται από τον g. Αντιστρόφως, οποιοδήποτε πολλαπλάσιο 'm του g μπορεί να ληφθεί με την επιλογή u = ms και v = mt, όπου s και t είναι οι ακέραιοι της ταυτότητας Bézout. Αυτό μπορεί να φανεί από τον πολλαπλασιασμό της ταυτότητας Bézout επί m,
- mg = msa + mtb.
Ως εκ τούτου, το σύνολο όλων των αριθμώνua + vb είναι ισοδύναμο με το σύνολο των πολλαπλασίων m του g. Με άλλα λόγια, το σύνολο όλων των πιθανών αθροισμάτων των ακεραίων πολλαπλασίων των δύο αριθμών(a και b) είναι ισοδύναμο με το σύνολο των πολλαπλασίων του ΜΚΔ(a, b). Ο ΜΚΔ λέγεται ότι είναι η γεννήτρια του ιδανικού του a και b. Ο ορισμός αυτός του ΜΚΔ οδήγησε στις σύγχρονες αφηρημένες αλγεβρικές έννοιες του κύριου ιδεώδους (ένα ιδεώδες που παράγεται από ένα μόνο στοιχείο) και των ακέραιου πεδίου κυριών ιδεωδών (ένα ακέραιο πεδίο στο οποίο κάθε ιδεώδες είναι ένα κύριο ιδεώδες).
Ορισμένα προβλήματα μπορούν να επιλυθούν με αυτό το αποτέλεσμα.[57] Για παράδειγμα, σκεφτείτε δύο κούπες μέτρησης του όγκου a και b. Με την προσθήκη / αφαίρεση πολλαπλάσιων του πρώτου κυπέλλου και πολλαπλάσιων του δεύτερου κυπέλλου, κάθε όγκος ua + vb μπορεί να μετρηθεί. Οι όγκοι αυτοί είναι όλοι πολλαπλάσιοι τουg = ΜΚΔ(a, b).
Διευρυμένος Ευκλείδειος αλγόριθμος[Επεξεργασία | επεξεργασία κώδικα]
Οι ακέραιοι s και t της ταυτότητας Bézout μπορούν να υπολογιστούν αποδοτικά χρησιμοποιώντας τον διευρυμένο Ευκλείδειο αλγόριθμο . Αυτή η επέκταση προσθέτει δύο αναδρομικές εξισώσεις στον αλγόριθμο του Ευκλείδη [ 58 ]
- sk = sk−2 − qksk−1
- tk = tk−2 − qktk−1
με τις τιμές έναρξης
- s−2 = 1, t−2 = 0
- s−1 = 0, t−1 = 1.
Χρησιμοποιώντας αυτή την αναδρομή,οι ακέραιοι Bézout s και t δίνονται από τις s = sN και t = tN , όπου Ν είναι το βήμα στο οποίο ο αλγόριθμος τερματίζει με rN = 0.
Η ισχύς αυτής της προσέγγισης μπορεί να αποδειχθεί με επαγωγή. Ας υποθέσουμε ότι ο αναδρομικός τύπος είανι σωστός μέχρι και το βήμα k − 1 του αλγορίθμου.Με άλλα λόγια, ας υποθέσουμε ότι
- rj = sj a + tj b
για όλα τα j μικρότερα του k . Το k στάδιο του αλγορίθμου δίνει την εξίσωση
- rk = rk−2 − qkrk−1.
Δεδομένου ότι υποθέσαμε ότι ο αναδρομικός τύπος είναι σωστός για rk−2 και rk−1 , μπορούν να εκφραστούν ως προς τις μεταβλητές s και t ,
- rk = (sk−2 a + tk−2 b) − qk(sk−1 a + tk−1 b).
Αναδιατάσσοντας αυτήν την εξίσωση παίρνουμε τον αναδρομικό τύπο για το βήμα k , όπως απαιτείται
- rk = sk a + tk b = (sk−2 − qksk−1) a + (tk−2 − qktk−1) b.
Μέθοδος πίνακα[Επεξεργασία | επεξεργασία κώδικα]
Οι ακέραιοι s και t μπορεί επίσης να βρεθεί χρησιμοποιώντας μία ισοδύναμη μέθοδο πίνακα. [ 59 ] Η σειρά των εξισώσεων του αλγορίθμου του Ευκλείδη
- a = q0 b + r0
- b = q1 r0 + r1
- …
- rN−2 = qN rN−1 + 0
μπορεί να γραφτεί ως προϊόν 2-επί-2 πινάκων πολλαπλασιάζοντας ένα δισδιάστατο υπόλοιπο διανύσματος
Έστω ότι M αντιπροσωπεύει το γινόμενο του συνόλου των πινάκων
Αυτό απλοποιεί την Ευκλείδειο αλγόριθμο στη μορφή
Για να εκφράσουμε το g ως ένα γραμμικό συνδυασμό του a και του b ,και οι δύο πλευρές της εξίσωσης αυτής μπορούν να πολλαπλασιαστούν με τον αντίστροφο του πίνακα Μ . [ 59 ] [ 60 ] Η ορίζουσα του Μ ισούται με −1)N+1 , αφού ισούται με το γινόμενο των καθοριστικών παραγόντων των πινάκων, καθένα από τα οποία είναι αρνητικά. Δεδομένου ότι ο καθοριστικός παράγοντας του Μ δεν είναι ποτέ μηδέν, το διάνυσμα των τελευταίων υπολοίπων μπορεί να επιλυθεί χρησιμοποιώντας τον αντίστροφο του Μ
Δεδομένου ότι η πρώτη εξίσωση δίνει
- g = (−1)N+1 ( m22 a − m12 b)
οι δύο ακέραιοι αριθμοί της ταυτότητας του Bézout είναι s = (−1)N+1m22 και t = (−1)Nm12 . Η μέθοδος των πινάκων είναι τόσο αποτελεσματική όσο η χρήση του αναδρομικού τύπου, με δύο πολλαπλασιασμούς και δύο προσθέσεις ανά βήμα του Ευκλείδειου αλγορίθμου.
Λήμμα του Ευκλείδη και μοναδική παραγοντοποίηση[Επεξεργασία | επεξεργασία κώδικα]
Η ταυτότητα Bézout είναι απαραίτητη για πολλές εφαρμογές του αλγορίθμου του Ευκλείδη, όπως αποδεικνύουν οι μοναδικές παραγοντοποιήσεις αριθμών σε πρώτους παράγοντες.[58] Για να φανεί αυτό, ας υποθέσουμε ότι ένας αριθμός L μπορεί να γραφτεί ως γινόμενο δύο παραγόντων u και v , δηλαδή , L = uv . Αν κάποιος άλλος αριθμός w διαιρεί επίσης τον L , αλλά είναι πρώτοι μεταξύ τους με τον u , τότεο w πρέπει να διαιρέσει τον ν ,σύμφωνα με την επόμενη πρόταση: Εάν ο μέγιστος κοινός διαιρέτης των u και w είναι 1, τότε οι ακέραιοι s και t μπορεί να βρεθούν, έτσι ώστε
- 1 = su + tw
από την ταυτότητα του Bézout . Πολλαπλασιάζοντας και τις δύο πλευρές με v παίρνουμε τη σχέση
- v = suv + twv = sL + twv
Αφού το w διαιρεί τους δύο όρους στη δεξιά πλευρά, θα πρέπει επίσης να διαιρεί και την αριστερή πλευρά, v . Το αποτέλεσμα είναι γνωστό ως λήμμα του Ευκλείδη.[59] Συγκεκριμένα, αν ένας πρώτος αριθμός διαιρεί το L , τότε θα πρέπει να διαιρεί τουλάχιστον έναν παράγοντα του L . Αντιστρόφως, εάν ένας αριθμός w είναι πρώτος με κάθε ένα από μια σειρά αριθμών a1, a2, …, an, τότε ο w είναι επίσης πρώτος με το γινόμενό τους, a1 × a2 × … × an.[59] Το λήμμα του Ευκλείδη θέλει να αποδείξει ότι κάθε αριθμός παραγοντοποιήται σε πρώτους αριθμούς.[60] Για να το δούμε αυτό, ας υποθέσουμε το αντίθετο, ότι υπάρχουν δηλαδή δύο ανεξάρτητες παραγοντοποιήσεις της L σε m και n πρώτους όρους, αντίστοιχα,
- L = p1p2…pm = q1q2…qn .
Δεδομένου ότι κάθε πρώτος αριθμός p διαιρεί τον L σύμφωνα με την υπόθεση, θα πρέπει ακόμα να διαιρεί έναν από τους όρους q. Δεδομένου ότι κάθε q είναι πρώτος αριθμός , πρέπει να ισχύει ότι p = q . Διαιρούμενοι διαρκώς με p όρους προκύπτει ότι κάθε p έχει έναν ίσο ομόλογο q .Οι δύο βασικές παραγοντοποιήσεις είναι πανομοιότυπες, με εξαίρεση τη σειρά τους. Η μοναδική παραγοντοποίηση των αριθμών σε πρώτους αριθμούς έχει πολλές εφαρμογές σε μαθηματικές αποδείξεις, όπως φαίνεται παρακάτω.
Γραμμικές Διοφαντικές εξισώσεις[Επεξεργασία | επεξεργασία κώδικα]
Διοφαντικές εξισώσεις είναι εξισώσεις στις οποίες οι λύσεις περιορίζονται σε ακέραιους αριθμούς.Πήραν το όνομά τους από τον μαθηματικό του 3ου αιώνα Αλέξανδρο Διόφαντος.[61] Μια τυπική γραμμική Διοφαντική εξίσωση αναζήτησης ακεραίων x και y είναι η [62]
- ax + by = c
όπου a , b και c είναι ακέραιοι αριθμοί . Αυτό μπορεί να γραφεί ως εξίσωση για x στην modular αριθμητική
- ax ≡ c mod b.
Έστω g είναι ο μέγιστος κοινός διαιρέτης των a και b . Και οι δύο όροι στη σχέση ax + by διαιρούνται με το g.Ως εκ τούτου, ο c πρέπει επίσης να διαιρείται με το g , διαφορετικά η εξίσωση δεν έχει λύσεις. Διαιρώντας και τις δύο πλευρές με c / g , η εξίσωση μπορεί να μικρύνει με την ταυτότητα του Bezout
- sa + tb = g ,
όπου s και t μπορεί να βρεθούν από τον διευρυμένο Ευκλείδειο αλγόριθμο.[63] Αυτό παρέχει μία λύση για το Διοφαντική εξίσωση, x1 = s (c/g) και y1 = t (c/g). . Σε γενικές γραμμές, μια γραμμική Διοφαντική εξίσωση δεν έχει καμία λύση ή έχει άπειρο αριθμό λύσεων.[64] Για να βρούμε το τελευταίο, εξετάζουμε δύο λύσεις, (x1, y1) και (x2, y2)
- ax1 + by1 = c = ax2 + by2
ή ισοδύναμα
- a(x1 − x2) = b(y2 − y1).
Ως εκ τούτου, η μικρότερη διαφορά μεταξύ δύο x λύσεων είναι b / g , ενώ η μικρότερη διαφορά μεταξύ δύο y λύσεων είναι a / g . Ετσι, οι λύσεις μπορούν να εκφραστούν ως
- x = x1 − bt/g
- y = y1 + at/g.
Επιτρέποντας την τιμή του t να ποικίλλει σε όλους τους πιθανούς ακέραιους, μια άπειρη οικογένεια λύσεων μπορεί να παράγεται από ένα μόνο διάλυμα (x1, y1) . Εάν οι λύσεις απαιτούνται να είναι θετικοί ακέραιοι (x > 0, y > 0), μόνο ένας πεπερασμένος αριθμός λύσεων μπορεί να είναι δυνατός. Αυτός ο περιορισμός των αποδεκτών λύσεων επιτρέπει συστήματα Διοφαντικών εξισώσεων να επιλύονται με περισσότερους αγνώστους [65].Αυτό είναι αδύνατο για ένα σύστημα γραμμικών εξισώσεων , όταν οι λύσεις μπορεί να είναι ένας οποιοσδήποτε πραγματικός αριθμός.
Πολλαπλασιαστικά αντίστροφα και ο αλγόριθμος RSA[Επεξεργασία | επεξεργασία κώδικα]
Ένα πεπερασμένο σώμα είναι ένα σύνολο αριθμών με τέσσερις γενικευμένες πράξεις. Οι πράξεις ονομάζονται πρόσθεση, αφαίρεση, πολλαπλασιασμός και διαίρεση και έχουν τις συνήθεις ιδιότητές τους, όπως commutativity, συσχέτιση και distributivity. Ένα παράδειγμα ενός πεπερασμένου σώματος είναι το σύνολο από 13 αριθμούς {0, 1, 2, …, 12} με modular αριθμητική . Στον τομέα αυτό, τα αποτελέσματα από κάθε μαθηματική πράξη (πρόσθεση / αφαίρεση / πολλαπλασιασμός / διαίρεση) μειώνονται στο modulo 13. Έτσι, πολλαπλάσια του 13, προστίθενται ή αφαιρούνται έως ότου το αποτέλεσμα γίνει μέσα στο εύρος 0-12. Για παράδειγμα, αποτέλεσμα του 5 × 7 = 35 mod 13 = 9 . Τέτοια πεπερασμένα σώματα μπορούν να εφαρμοστούν για κάθε πρώτο αριθμό p.Χρησιμοποιώντας πιο εξελιγμένε ερμηνείες, μπορούν επίσης να εφαρμοστούν για δύναμη m ενός πρώτου αριθμού p . Τα πεπερασμένα σώματα συχνά αποκαλούνται τομείς Galois και σε συντομογραφία γράφονται ως GF(p) ή GF(p m). Σε ένα τέτοιο σώμα με m αριθμούς, κάθε μη μηδενικό στοιχείο a έχει ένα μοναδικό αντίστροφο πολλαπλασιαστικό modular,a−1 τέτοιο ώστε aa−1 = a−1a ≡ 1 mod m . Αυτό το αντίστροφο μπορεί να βρεθεί λύνοντας αντίστοιχα την εξίσωση ax ≡ 1 mod m ,[66] ή την ισοδύναμη Διοφαντική εξίσωση [67]
- ax + my = 1.
Αυτή η εξίσωση μπορεί να λυθεί από τον Ευκλείδειο αλγόριθμο, όπως περιγράφηκε παραπάνω.Βρίσκοντας πολλαπλασιαστικά αντίστροφα είναι ένα ουσιαστικό βήμα στον RSA αλγόριθμο , ο οποίος χρησιμοποιείται ευρέως στο ηλεκτρονικό εμπόριο .Συγκεκριμένα, η εξίσωση που καθορίζει τον ακέραιο χρησιμοποιείται για να αποκρυπτογραφήσει το μήνυμα.[68] Σημειώστε ότι αν και ο αλγόριθμος RSA χρησιμοποιεί δακτύλιους αντί για σώματα, ο Ευκλείδειος αλγόριθμος μπορεί ακόμη να χρησιμοποιηθεί για να βρει ένα πολλαπλασιαστικό αντίστροφο, αν υπάρχει. Ο Ευκλείδειος αλγόριθμος έχει και άλλες εφαρμογές σε κώδικες διόρθωτές λαθών. Για παράδειγμα, μπορεί να χρησιμοποιηθεί ως εναλλακτική λύση για τον αλγόριθμο Berlekamp-Massey για την αποκωδικοποίηση κωδίκων BCH και Reed-Solomon ,οι οποίοι βασίζονται στους Galois τομείς.[69]
Κινέζικο θεώρημα υπολοίπων[Επεξεργασία | επεξεργασία κώδικα]
Ο Ευκλείδιος αλγόριθμος μπορεί επίσης να χρησιμοποιηθεί για την επίλυση πολλαπλών γραμμικών Διοφαντικών εξισώσεων.[70] Τέτοιες εξισώσεις προκύπτουν στο Κινέζικο θεώρημα υπολοίπου , το οποίο περιγράφει μία νέα μέθοδο για την αντιπροσώπευση ενός ακεραίου x . Αντί να εκπροσωπείται ένας ακέραιος από τα ψηφία του, μπορεί να εκπροσωπείται από το υπόλοιπο του xi modulo, ένα σύνολο N σχετικά πρώτων αριθμών mi .[71]
- x1 ≡ x mod m1
- x2 ≡ x mod m2
- …
- xN ≡ x mod mN
Ο στόχος είναι να προσδιοριστεί το x από το υπόλοιπο του N με το xi. Η λύση είναι να συνδυάσει τις πολλαπλές εξισώσεις σε μια ενιαία γραμμική Διοφαντική εξίσωση με ένα πολύ μεγαλύτερο συντελεστή M , που είναι το γινόμενο όλων των επιμέρων moduli mi, και να καθορίσει το Mi ,
- Mi = M / mi
Ετσι, κάθε Mi είναι το γινόμενο όλων των moduli εκτός του mi . Η λύση εξαρτάται από την εύρεση N νέων αριθμών hi έτσι ώστε να ισχύει
- Mihi ≡ 1 mod mi
Με αυτούς τους αριθμούς hi , οποιοσδήποτε ακέραιος x μπορεί να ανακατασκευαστεί από τα υπόλοιπα xi από την εξίσωση
- x ≡ (x1M1h1 + x2M2h2 + … + xNMNhN ) mod M
Δεδομένου ότι αυτοί οι αριθμοί hi είναι τα πολλαπλασιαστικά αντίστροφα του Mi , μπορούν να βρεθούν χρησιμοποιώντας τον αλγόριθμο του Ευκλείδη, όπως περιγράφηκε στην προηγούμενη ενότητα.
Δέντρο Stern-Brocot[Επεξεργασία | επεξεργασία κώδικα]
Η αλληλουχία των αφαιρέσεων που χρησιμοποιείται από τον Ευκλείδειο αλγόριθμο δίνει μια διαδρομή από τη ρίζα του Δέντρου Stern-Brocot σε οποιαδήποτε δεδομένο ρητό αριθμό. Το γεγονός αυτό μπορεί να χρησιμοποιηθεί για να αποδειχθεί ότι υπάρχει μια 1-1 αντιστοιχία μεταξύ των κορυφών των δέντρων και των θετικών ρητών αριθμών. Για παράδειγμα, το 3/4 μπορεί να βρεθεί ξεκινώντας από την ρίζα, προχωρώντας προς τα αριστερά μια φορά, και στη συνέχεια, προς τα δεξιά δύο φορές.
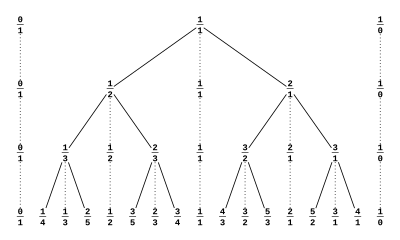
Ο Ευκλείδειος αλγόριθμος είναι σχεδόν το ίδιο με το Calkin-Wilf δέντρο . Η διαφορά είναι ότι η διαδρομή αντιστρέφεται: αντί να παράγει μια διαδρομή από τη ρίζα του δέντρου σε ένα στόχο, παράγει μια διαδρομή από το στόχο προς τη ρίζα.
Συνεχή κλάσματα[Επεξεργασία | επεξεργασία κώδικα]
Ο Ευκλείδειος αλγόριθμος έχει μια στενή σχέση με τα συνεχή κλάσματα .[72] Η σειρά των εξισώσεων μπορεί να γραφεί στη μορφή
Ο τελευταίος όρος στη δεξιά πλευρά είναι πάντα ίσος με τον αντίστροφο της αριστερής πλευράς της επόμενης εξίσωσης. Έτσι, οι δύο πρώτες εξισώσεις μπορούν να συνδυαστούν για να σχηματίσουν
Η τρίτη εξίσωση μπορεί να χρησιμοποιηθεί για να αντικαταστήσει τον όρο r1/r0 , αποδίδοντας
Η τελική αναλογία από το υπόλοιπο του rk/rk−1 μπορεί πάντα να αντικατασταθεί χρησιμοποιώντας την επόμενη εξίσωση στη σειρά, μέχρι την τελική εξίσωση. Το αποτέλεσμα είναι ένα συνεχές κλάσμα
Στο αριθμητικό παραπάνω παράδειγμα , ο ΜΚΔ (1071, 462) υπολογίστηκε και το πηλίκο qk ήταν 2, 3 και 7, αντίστοιχα. Ως εκ τούτου, το κλάσμα 1071/462 μπορεί να γραφεί
όπως μπορεί να επιβεβαιωθεί από τον υπολογισμό.
Αλγόριθμοι Παραγοντοποίησης[Επεξεργασία | επεξεργασία κώδικα]
Ο υπολογισμός ενός μέγιστου κοινού διαιρέτη είναι ένα ουσιαστικό βήμα σε πολλές παραγοντοποιήσεις ακεραίων αλγορίθμων,[73] όπως αλγόριθμος r του Pollard ,[74] ο αλγόριθμος του Shor,[75] η μέθοδος παραγοντοποίησης Ντίξον,[76] και η ελλειπτική παραγοντοποίηση καμπύλης Lenstra .[77] Ο Ευκλείδειος αλγόριθμος μπορεί να χρησιμοποιηθεί για να βρεθεί το ΜΚΔ αποτελεσματικά. Συνεχή παραγοντοποιημένα κλάσματα χρησιμοποιούν συνεχή κλάσματα, τα οποία καθορίζονται χρησιμοποιώντας τον αλγόριθμο του Ευκλείδη.[78]
Αλγοριθμική αποδοτικότητα[Επεξεργασία | επεξεργασία κώδικα]

Η υπολογιστική αποδοτικότητα του αλγορίθμου του Ευκλείδη έχει μελετηθεί διεξοδικά.[79] Αυτή η αποτελεσματικότητα μπορεί να περιγραφεί από τον αριθμό των βημάτων της διαίρεσης που απαιτεί ο αλγόριθμος, πολλαπλασιαζόμενο με το υπολογιστικό κόστος κάθε βήματος. Η πρώτη γνωστή ανάλυση του αλγορίθμου του Ευκλείδη έγινε από τον A.-A.-L. Reynaud το 1811,[80] ο οποίος έδειξε ότι ο αριθμός των βημάτων διαίρεσης στην είσοδο των ( u , v ) οριοθετείται από το v.Αργότερα το βελτίωσε αυτό σε ν / 2 + 2. Μετέπειτα , το 1841,ο P.-J.-E. Finck έδειξε [81] ότι ο αριθμός των βημάτων διαίρεσης είναι το πολύ 2 log2 v + 1 , και ως εκ τούτου ο αλγόριθμος του Ευκλείδη τρέχει σε πολυωνυμικό χρόνο στο μέγεθος της εισόδου. βλέπε επίσης [82] Η ανάλυση του τελειοποιήθηκε από τον Gabriel Lamé σε 1844,[83] ο οποίος έδειξε ότι ο αριθμός των βημάτων που απαιτούνται για την λύση δεν είναι ποτέ περισσότερα από πέντε φορές τον αριθμό h της βάσης-10 ψηφίων του μικρότερου αριθμού b .[84][85] Αφού το υπολογιστικό βάρος κάθε βήματος είναι συνήθως της τάξης h , η συνολική δαπάνη μεγαλώνει κατά h2.
Αριθμός βημάτων[Επεξεργασία | επεξεργασία κώδικα]
Ο αριθμός των βημάτων για τον υπολογισμό του ΜΚΔ δύο φυσικών αριθμών, a και b , μπορεί να συμβολίζεται με T(a, b) .[86] Αν g είναι ο ΜΚΔ του a και b , τότε a = mg και b = ng για δύο πρώτους μεταξύ τους αριθμούς m και n . Τότε
- T(a, b) = T(m, n)
όπως μπορεί να φανεί διαιρώντας όλα τα βήματα στην Ευκλείδειο αλγόριθμο g .[87] Με το ίδιο επιχείρημα, ο αριθμός των βημάτων παραμένει ο ίδιος, αν a και b πολλαπλασιάζονται με έναν κοινό συντελεστή w: T(a, b) = T(wa, wb). Ως εκ τούτου, ο αριθμός των βημάτων Τ μπορεί να ποικίλλει δραματικά μεταξύ γειτονικών ζευγών αριθμών, όπως T(a, b) και T(a, b + 1) , ανάλογα με το μέγεθος των δύο ΜΚΔ.
Η αναδρομική φύση του αλγορίθμου του Ευκλείδη δίνει μια άλλη εξίσωση
- T(a, b) = 1 + T(b, r0) = 2 + T(r0, r1) = … = N + T(rN−2, rN−1) = N + 1
όπου T(x, 0) = 0 σύμφωνα με την υπόθεση.[86]
Η χειρότερη περίπτωση αριθμού βημάτων[Επεξεργασία | επεξεργασία κώδικα]
Αν ο Ευκλείδειος αλγόριθμος απαιτεί N βήματα για ένα ζευγάρι φυσικών αριθμών a > b > 0 , οι μικρότερες τιμές των a και b για την οποία αυτός αληθεύει, είναι οι αριθμοί Fibonacci FN+2 και FN+1 , αντίστοιχα.[88] Αυτό μπορεί να αποδειχθεί με επαγωγή .[89] Εάν N = 1, ο b διαιρεί τον a ακριβώς.Οι μικρότεροι φυσικοί αριθμοί για τους οποίους ισχύει είναι b = 1 και a = 2, τα οποία είναι τα F2 και F3 , αντιστοίχως. Ας υποθέσουμε τώρα ότι το αποτέλεσμα ισχύει για όλες τις τιμές του Ν έως M − 1 . Το πρώτο βήμα ενός αλγορίθμου με Μ-βήματα είναι a = q0b + r0 , και το δεύτερο βήμα είναι b = q1r0 + r1 . Δεδομένου ότι ο αλγόριθμος είναι αναδρομικός,απαιτούνται M − 1 βήματα για να βρεθεί ο ΜΚΔ (b, r0) και οι μικρότερες τιμές τους είναι FM+1 και FM . Έχουμε συνεπώς την μικρότερη τιμή του a , όταν q0 = 1 , το οποίο δίνει a = b + r0 = FM+1 + FM = FM+2 . Η απόδειξη αυτή, η οποία δημοσιεύθηκε από τον Gabriel Lamé το 1844, αντιπροσωπεύει την αρχή τηςυπολογιστικής θεωρίας πολυπλοκότητας ,[90] καθώς επίσης και την πρώτη πρακτική εφαρμογή των αριθμών Fibonacci.[88] Το αποτέλεσμα αυτό αρκεί για να δείξει ότι ο αριθμός των βημάτων στον αλγόριθμο του Ευκλείδη δεν μπορεί ποτέ να είναι μεγαλύτερος από πέντε φορές τον αριθμό των ψηφίων του (βάση 10).[91] Για το αν ο αλγόριθμος απαιτεί Ν βήματα, τότε ο b είναι μεγαλύτερος ή ίσος με το FN+1 το οποίο με τη σειρά του είναι μεγαλύτερο ή ίσο με φN−1 , όπου φ είναι η χρυσή τομή.Αφού b ≥ φN−1, τότε N − 1 ≤ logφb. Αφού log10φ > 1/5, (N − 1)/5 < log10φ logφb = log10b . Έτσι, N ≤ 5 log10b . Επομένως, ο Ευκλείδειος αλγόριθμος χρειάζεται πάντα λιγότερες από Ο ( h ) διαιρέσεις, όπου h είναι ο αριθμός των ψηφίων του μικρότερου αριθμού b .
Υπολογιστική δαπάνη ανά βήμα[Επεξεργασία | επεξεργασία κώδικα]
Σε κάθε βήμα k τoy Ευκλείδειoυ αλγορίθμου, το πηλίκο qk και υπόλοιπο rk υπολογίζονται για ένα δεδομένο ζεύγος ακεραίων rk−2 και rk−1
- rk−2 = qk rk−1 + rk.
Η υπολογιστική δαπάνη ανά βήμα σχετίζεται κυρίως με την εύρεση του qk , δεδομένου ότι το υπόλοιπο rk μπορεί να υπολογιστεί γρήγορα από rk−2, rk−1, και qk
- rk = rk−2 − qk rk−1.
Η υπολογιστική δαπάνη διαίρεσης h -bit αριθμούς ως κλίμακες O(h(ℓ+1)), όπου ℓ είναι το μήκος του πηλίκου.[92]
Για λόγους σύγκρισης,ο αρχικός αλγόριθμος του Ευκλείδη που χρησιμοποιεί τη μέθοδο της αφαίρεσης,μπορεί να είναι πολύ πιο αργός. Μια ακέραια διαίρεση είναι ισοδύναμη με το πηλίκο Q προς τον αριθμό των αφαιρέσεων. Εάν η αναλογία του a και του Β είναι πολύ μεγάλη, το πηλίκο είναι μεγάλο και θα απαιτηθούν πολλές αφαιρέσεις. Από την άλλη πλευρά, έχει δειχθεί ότι τα πηλίκα είναι πολύ πιθανό να είναι μικροί ακέραιοι. Η πιθανότητα ενός δεδομένου πηλίκου q είναι περίπου ln|u/(u − 1)| όπου u = (q + 1)2.[93] Για παράδειγμα, η πιθανότητα ενός πηλίκου 1, 2, 3 ή 4 είναι περίπου 41,5%, 17,0%, 9,3% και 5,9%, αντίστοιχα. Δεδομένου ότι η λειτουργία της αφαίρεσης είναι πιο γρήγορη από ό, τι της διαίρεσης, ιδιαίτερα για μεγάλους αριθμούς,[94]η μέθοδος του Ευκλείδη που βασίζεται στην αφαίρεση είναι "ανταγωνιστική" με τη μέθοδο της διαίρεσης.[95] Αυτό αξιοποιείται στην δυαδική έκδοση του αλγορίθμου του Ευκλείδη.[96]
Συνδυάζοντας τον εκτιμώμενο αριθμό των βημάτων με την εκτιμώμενη υπολογιστική δαπάνη ανά βήμα φαίνεται ότι ο αλγόριθμος του Ευκλείδη μεγαλώνει συγγραμικά (h2) , με τον μέσο αριθμό των ψηφίων "h" των δύο πρώτων αριθμών a και b . Έστω h0, h1, …, hN−1 -1 αντιπροσωπεύουν τον αριθμό των ψηφίων στο πλαίσιο των διαδοχικών υπολοίπων r0, r1, …, rN−1 . Δεδομένου ότι ο αριθμός των βημάτων "N" αναπτύσσεται γραμμικά με "h" , ο χρόνος είναι που οριοθετείται από
Αποδοτικότητα των εναλλακτικών μεθόδων[Επεξεργασία | επεξεργασία κώδικα]
Ο Αλγόριθμος του Ευκλείδη χρησιμοποιείται ευρέως στην πράξη, ιδίως για τους μικρούς αριθμούς, λόγω της απλότητάς του. Για λόγους σύγκρισης, η αποτελεσματικότητα των εναλλακτικών αλγόριθμων του Ευκλείδη μπορεί να προσδιοριστεί.
Μια αναποτελεσματική προσέγγιση για την εύρεση του ΜΚΔ δύο φυσικών αριθμών a και Β είναι να υπολογιστούν όλοι οι κοινοί διαιρέτες τους.ο ΜΚΔ είναι τότε ο μεγαλύτερος κοινός διαιρέτης. Οι κοινοί διαιρέτες μπορούν να βρεθούν διαιρώντας τους δύο αριθμούς με διαδοχικούς ακέραιους από 2 έως τον μικρότερο αριθμό b . Ο αριθμός των βημάτων της προσέγγισης αυτής αυξάνει γραμμικά με το b , ή εκθετικά με τον αριθμό των ψηφίων. Μια άλλη προσέγγιση είναι αναποτελεσματική για να βρει τους πρωταρχικούς παράγοντες του ενός ή και των δύο αριθμών. Όπως σημειώνεται ανωτέρω , ο ΜΚΔ ισούται με το γινόμενο από των πρώτων κοινών παραγόντων των α και b.[8] Οι παρούσες μέθοδοι για την παραγοντοποίηση είναι επίσης αναποτελεσματικές. πολλά σύγχρονα συστήματα κρυπτογράφησης, ακόμη στηρίζονται στην εν λόγω αναποτελεσματικότητα.[11]
Ο δυαδικός αλγόριθμος του ΜΚΔ είναι μια αποτελεσματική εναλλακτική λύση που περιλαμβάνει διαίρεση με πιο γρήγορες διαδικασίες, αξιοποιώντας τη δυαδική αναπαράσταση που χρησιμοποιείται από τους υπολογιστές. .[97][98] Ωστόσο, αυτή η εναλλακτική επίσης εκτιμάται της τάξης του |O(h²)]]. Είναι γενικά πιο γρήγορη από τον Ευκλείδειο αλγόριθμο για πραγματικούς υπολογιστές, μολονότι εξελίσεται με τον ίδιο τρόπο.[99] επιπλέον η αποτελεσματικότητά του μπορεί να φανεί εξετάζοντας μόνο τα μεγαλύτερα ψηφία των δύο αριθμών α και b .[100][101] ο δυαδικός αλγόριθμος μπορεί να επεκταθεί και σε άλλες βάσεις ( k -ary αλγόριθμοι), ),[102] με έως και πενταπλάσια αύξηση στην ταχύτητα..[103]
Μια αναδρομική προσέγγιση για όλους τους μεγάλους ακεραίους (με περισσότερα από 25.000 ψηφία) οδηγεί σε subquadratic αλγορίθμων ακεραίων για τον ΜΚΔ ,[104] όπως αυτές της Schönhage,[105][106] και Stehle και Zimmermann.[107] Αυτοί οι αλγόριθμοι εκμεταλλεύονται τον 2 × 2 μορφής πίνακα του Ευκλείδιου αλγόριθμου που δίνεται παραπάνω . Αυτές οι μέθοδοι γενικά της τάξης του O(h (log h)2 (log log h))..[99][108]
Άλλα συστήματα αριθμών[Επεξεργασία | επεξεργασία κώδικα]
Όπως περιγράφεται παραπάνω, ο Ευκλείδειος αλγόριθμος χρησιμοποιείται για να βρούμε τον μέγιστο κοινό διαιρέτη δύο φυσικών αριθμών (θετικοί ακέραιοι). Ωστόσο, μπορεί να γενικευτεί στους πραγματικούς αριθμούς, και σε πιο εξωτικά συστήματα αριθμών, όπως πολυώνυμα , τετραγωνικοί ακέραιοι και Hurwitz quaternions . Στις τελευταίες περιπτώσεις, ο Ευκλείδειος αλγόριθμος χρησιμοποιείται για να καταδείξει την κρίσιμη ιδιότητα της μοναδικής παραγοντοποίησης, δηλαδή, ότι οι αριθμοί μπορούν να αναλυθούν κατά μοναδικό τρόπο σε ανάγωγα στοιχεία , οι αντίστιχοι των πρώτων αριθμών. Αυτής της μορφής η παραγοντοποίηση είναι ιδιαιτέρως χρήσιμη για πολλές αποδείξεις της θεωρίας αριθμών.
Ρητοί και πραγματικοί αριθμοί[Επεξεργασία | επεξεργασία κώδικα]
Ο αλγόριθμος του Ευκλείδη μπορεί να εφαρμοστεί σε πραγματικούς αριθμούς , όπως περιγράφεται από τον Ευκλείδη στο δέκατο βιβλίο των Στοιχείων. ο στόχος του αλγορίθμου είναι να προσδιορίσει έναν πραγματικό αριθμό g τέτοιον ώστε δύο δοσμένοι πραγματικοί αριθμοί, α και β ,να είναι ακέραια πολλαπλάσια του: α = mg και b = ng , όπου m και n είναι ακέραιοι.[27] Αυτή η ταυτοποίηση είναι ισοδύναμη με την εύρεση μια ακέραια σχέση μεταξύ των πραγματικών αριθμών α και β.δηλαδή, προσδιορίζει ακέραιους s και t , έτσι ώστε sa + tb = 0.Ευκλείδιος αλγόριθμος χρησιμοποιείται για την αντιμετώπιση του ζητήματος των ασύμμετρων μηκών .[109][110]
Ο αλγόριθμος του ευκλείδη για τους πραγματικούς αριθμούς διαφέρει από τον αντίστοιχο για ακεραίους σε δύο σημεία. Πρώτον,τα υπόλοιπα rk είναι πραγματικοί αριθμοί, αν και τα πηλίκα qk είναι ακέραιοι, όπως και πριν. Δεύτερον, ο αλγόριθμος δεν είναι εγγυημένο πως θα ολοκληρωθεί σε πεπερασμένο αριθμό Ν των βημάτων. Αν συμβεί αυτό, το κλάσμα α / b είναι ένας ρητός αριθμός, δηλαδή, ο λόγος δύο ακεραίων
- a/b = mg/ng = m/n
και μπορεί να γραφτεί ως ένα πεπερασμένο συνεχές κλάσμα [q0; q1, q2, …, qN[q0; q1, q2, …, qN. Αν ο αλγόριθμος δεν σταματά, το κλάσμα α / b είναι ένας άρρητος αριθμός και μπορεί να περιγραφεί σαν ένα άπειρο συνεχές κλάσμα [q0; q1, q2, …]. Παραδείγματα από άπειρα συνεχή κλάσματα είναι η χρυσή τομή φ = [1? 1, 1, ...] και η τετραγωνική ρίζα του δύο,√2 = [1; 2, 2, …]. Σε γενικές γραμμές, ο αλγόριθμος είναι απίθανο να σταματήσει, δεδομένου ότι σχεδόν όλες οι αναλογίες α / β των δύο πραγματικών αριθμών είναι άρρητες.
Ένα άπειρο συνεχές κλάσμα μπορεί να σπάσει σε κάποιο στάδιο k [q0; q1, q2, …, qk] για να δώσει μια προσέγγιση του α / Β που γίνεται ολοένα καλύτερη καθώς το k αυξάνεται. Η προσέγγιση αυτή περιγράφεται από συκλίνοντες, ο αριθμητής και ο παρονομαστής είναι πρώτοι μεταξύ τους και συνδέονται με τη σχέση
- mk = qk mk−1 + mk−2
- nk = qk nk−1 + nk−2
όπου m−1 = n−2 = 1 and m−2 = n−1 = 0 είναι οι αρχικές τιμές της αναδρομικής σχέσης. Η συγκλίνουσα mk/nk είναι η καλύτερη ρητή προσέγγιση στο a/b με παρονομαστή nk::
Πολυώνυμα[Επεξεργασία | επεξεργασία κώδικα]
Πολυώνυμα σε μια μόνο μεταβλητή x μπορεί να προστεθούν, πολλαπλασιάστούν και να αναλυθούν σε ανάγωγα πολυώνυμα , τα οποία είναι τα ανάλογα των πρώτων αριθμών για τους ακέραιους αριθμούς. Ο μέγιστος κοινός διαιρέτης πολυώνυμο g(x) δύο πολυωνύμων a(x) and b(x) ορίζεται ως το γινόμενο των κοινών ανάγωγων πολυωνυμων τους, τα οποία μπορούν να προσδιοριστούν χρησιμοποιώντας τον Ευκλείδειο αλγόριθμο.[111] Η βασική διαδικασία είναι παρόμοια με τους ακέραιους. Σε κάθε βήμα "k" , ένα πηλίκο πολυώνυμο qk(x) και ένα υπόλοιπο πολυώνυμο rk(x) προσσδιορίζονται για να ικανοποιήσει την επαναληπτική εξίσωση
- rk−2(x) = qk(x) rk−1(x) + rk(x)
όπου r−2(x) = a(x) και r−1(x) = b(x). Το πολυώνυμο-πηλίκον επιλέγεται έτσι ώστε ο μεγαλύτερος όρος qk(x) rk−1(x) να ισούται με τον μεγαλύτερο όρο του rk−2(x);. αυτό εξασφαλίζει ότι ο βαθμός κάθε υπόλοιπου είναι μικρότερος από το βαθμό του προηγουμένου του deg[rk(x)] < deg[rk−1(x)]. Δεδομένου ότι ο βαθμός είναι ένας μη αρνητικός ακέραιος αριθμός, και δεδομένου ότι μειώνεται με κάθε βήμα, ο αλγόριθμος του Ευκλείδη ολοκληρώνεται σε έναν πεπερασμένο αριθμό βημάτων. Το τελικό μη μηδενικό υπόλοιπο είναι ο μέγιστος κοινός διαιρέτης των αρχικών δύο πολυώνυμα,a(x) και b(x).[112]
Για παράδειγμα, σκεφτείτε τα εξής δύο τετραγωνικά πολυώνυμα, στα οποίο κάθε παράγοντας αναλύεται σε δύο τετραγωνικά πολυώνυμα
- a(x) = x4 − 4x3 + 4 x2 − 3x + 14 = (x2 − 5x + 7)(x2 + x + 2)
και
- b(x) = x4 + 8x3 + 12x2 + 17x + 6 = (x2 + 7x + 3)(x2 + x + 2).
Διαιρώντας το a(x) με το b(x) προκύπτει ένα υπόλοιπο r0(x) = x3 + (2/3) x2 + (5/3) x − (2/3). Στο επόμενο βήμα, b(x) διαιρείται δια r0(x) δίνοντας ένα υπόλοιπο ,r1(x) = x2 + x + 2 . Τέλος, διαιρώντας r0(x) με r1(x) προκύπτει ένα μηδενικό υπόλοιπο, που δείχνει ότι το r1(x) είναι ο μέγιστος κοινός διαιρέτης των πολυώνυμων a(x) και b(x). Πολλές από τις εφαρμογές που περιγράφονται παραπάνω για τους ακέραιους αριθμούς μεταφέρονται στο πολυώνυμα.[113] Ο Ευκλείδειος αλγόριθμος μπορεί να χρησιμοποιηθεί για την επίλυση γραμμικών διοφαντικών εξισώσεων και κινεζικων προβληματων για τα υπόλοιπα των πολυωνύμων. συνεχή κλάσματα πολυωνύμων μπορούν επίσης να οριστούν.
Ο πολυωνυμικός Ευκλείδειος αλγόριθμος έχει και άλλες εφαρμογές, καθώς, όπως Sturm chains , μια μέθοδος για την μέτρηση του αριθμού των πραγματικών ριζών ενός πολυωνύμου εντός ενός δεδομένου διαστήματος στον πραγματικό άξονα. Αυτό έχει εφαρμογές σε πολλούς τομείς, όπως στο κριτήριο της σταθερότητας Routh-Hurwitz στη θεωρία ελέγχου .
Τέλος, δεν χρειάζεται οι συντελεστές των πολυωνύμων να ειναι ακέραιοι αριθμοί, πραγματικοί αριθμοί ή ακόμη και οι μιγαδικοί. Για παράδειγμα, οι συντελεστές μπορούν να εξαχθούν από ένα γενικό σώμα, όπως είναι τα πεπερασμένα σώματα GF(p) που περιγράφτηκαν ανωτέρω. Τα αντίστοιχα συμπεράσματα σχετικά με την Ευκλείδειο αλγόριθμο και τις εφαρμογές τους γενικεύονται και στον πολυωνυμικό αλγόριθμο.
Ακέραιοι Gaussian[Επεξεργασία | επεξεργασία κώδικα]

Οι ακέραιοι Gaussian είναι μιγαδικοί αριθμοί της μορφής α = u + vi , όπου "u" και "v" είναι απλοί ακέραιοι και i είναι η τετραγωνική ρίζα του -1 .[114] Με τον καθορισμό ενός αναλόγου Ευκλείδειου αλγόριθμο,οι Gaussian ακέραιοι ,μπορεί να αποδειχθεί ότι είναι μοναδικά κατασκευάσιμοι,σύμφωνα με το επιχείρημα above .[40] Αυτή η μοναδική παραγοντοποίηση είναι χρήσιμη σε πολλές εφαρμογές, όπως στις πυθαγόρειες τριάδες ή στην απόδειξη του θεώρηματος του Φερμά για τα άθροισμα των τετραγώνων δύο αριθμών .[114] Σε γενικές γραμμές, ο Ευκλείδειος αλγόριθμος είναι βολικός σε τέτοιες εφαρμογές, αλλά δεν είναι απαραίτητος, για παράδειγμα, τα θεωρήματα μπορούν συχνά να αποδειχθεί ,με άλλους τρόπους.
Ο Ευκλείδειος αλγόριθμος που αναπτύχθηκε για δύο Gaussian ακέραιους α και β είναι σχεδόν ίδιος με εκείνον για τους απλούς ακέραιους, αλλά διαφέρει σε δύο σημεία. Όπως και πριν, το έργο σε κάθε βήμα "k" είναι να προσδιορίσει ένα πηλίκο qk και ένα υπόλοιπο rk τέτοια ώστε
- rk = rk−2 − qk rk−1
όπου rk−2 = α, rk−1 = β, και κάθε υπόλοιπο είναι αυστηρά μικρότερο από το προηγούμενο του, |rk| < |rk−1|. Η πρώτη διαφορά είναι ότι τα πηλίκα και τα υπόλοιπα είναι ακέραιοι Gaussian, και έτσι είναι μιγαδικοί αριθμοί . Τα πηλίκα qk γενικά βρίσκονται στρογγυλοποιώντας τα πραγματικά και μιγαδικά μέρη της ακριβούς αναλογίας (όπως το μιγαδικό αριθμό α / β) στους πλησιέστερους ακέραιους. Η δεύτερη διαφορά έγκειται στην αναγκαιότητα του καθορισμού πώς ένα μιγαδικό υπόλοιπο μπορεί να είναι "μικρότερο" από ένα άλλο. Για να γίνει αυτό, ορίζουμε μια συνάρτηση f(u + vi) = u2 + v2 , η οποία μετατρέπει κάθε Gaussian ακέραιο u + vi σε έναν κανονικό ακέραιο. Μετά από κάθε βήμα "k" του Ευκλείδειου αλγόριθμου, η τιμή του υπολοίπου f(rk) είναι μικρότερη από την τιμή του προηγούμενου υπολοίπου, f(rk−1). Δεδομένου ότι η τιμή είναι ένας μη αρνητικός ακέραιος αριθμός και μειώνεται σε κάθε βήμα, ο Ευκλείδειος αλγόριθμος για Gaussian ακέραιους ολοκληρώνεται σε ένα πεπερασμένο αριθμό βημάτων. Το τελικό μη μηδενικό υπόλοιπο αποτελεί το ΜΚΔ(α, β), ο Gaussian ακέραιος με τη μεγαλύτερη τιμή που διαιρεί και το α και το β. Είναι μοναδικός με πολλαπλασιασμό με τη μονάδα, ± 1, ± ή i .
Πολλές από τις άλλες εφαρμογές του Ευκλείδειου αλγόριθμου μεταφέρονται στους Gaussian ακέραιους. Για παράδειγμα, μπορεί να χρησιμοποιηθεί για την επίλυση γραμμικών διοφαντικών εξισώσεων και Κινέζικα προβλήματα για τα υπολοιπα των Gaussian ακεραίων Συνεχή κλάσματα Gaussian ακεραίων μπορούν επίσης να οριστούν.
Ευκλείδειες δομές[Επεξεργασία | επεξεργασία κώδικα]
Μια σειρά από στοιχεία μεταξύ των οποίων γίνονται δυαδικές πράξεις ,+ και ·, ονομάζονται Euclidean domains όταν σχηματίζουν αντιμεταθετικό δακτύλιο R και, σε γενικές γραμμές, αν ο γενικός Ευκλείδειος αλγόριθμος μπορεί να εφαρμοστεί σε αυτούς [115][116]. Οι δύο πράξεις ενός τέτοιου δακτυλίου δεν χρειάζεται να είναι η πρόσθεση και πολλαπλασιασμός της συνήθους αριθμητικής.αντίθετα, μπορούν να είναι πιο γενικά, όπως οι πράξεις σε μια ομάδα ή σε ένα μονοειδές . Παρ 'όλα αυτά, αυτές οι γενικές πράξεις θα πρέπει να υπακούν τους κανόνες που διέπουν τις συνήθεις αριθμητικές πράξεις, όπως προσεταιριστικότητα, αντιμεταθετικότητα και επιμεριστικότητα .
ο γενικευμένος Ευκλείδειος αλγόριθμος απαιτεί μια "Ευκλείδεια συνάρτηση" , δηλαδή, μια απεικόνιση f από το "R" στο σύνολο των θετικών ακέραιων τέτοια ώστε, για κάθε δύο μη μηδενικά στοιχεία a και b του "R" ,να υπάρχουν "q" και "r" στο "R" τέτοια ώστε a =qb + r και f(r) < f(b). Ένα παράδειγμα αυτής της απεικόνισης είναι συνάρτηση που χρησιμοποιείται για να διατάξουμε του Gaussian ακέραιους . Η συνάρτηση f μπορεί να είναι η δύναμη ενός αριθμού, ή ο βαθμός ενός πολυωνύμου . Η βασική αρχή είναι ότι σε κάθε βήμα του αλγορίθμου η "f" μειώνεται συνεχώς. Ως εκ τούτου, εάν η "f" μπορεί να μειωθεί μόνο έναν πεπερασμένο αριθμό φορών, ο αλγόριθμος πρέπει να σταματήσει σε έναν πεπερασμένο αριθμό βημάτων. Η αρχή αυτή στηρίζεται σε μεγάλο βαθμό στην αρχή της καλής διάταξης των μη-αρνητικών ακεραίων.σε γενικές γραμμές, αυτό προϋποθέτει ότι κάθε σύνολο των μη-αρνητικών ακεραίων έχει ελάχιστο στοιχείο.
Το θεμελιώδες θεώρημα της αριθμητικής ισχύει για κάθε Ευκλείδεια δομή: Οποιοσδήποτε αριθμός από μία Ευκλείδεια δομη μπορεί να αναλυθεί κατά μοναδικό τρόπο σε ανάγωγα στοιχεία. Κάθε Ευκλείδεια δομή είναι πολλαπλασιαστικός δακτύλιος, αν και το αντίστροφο δεν ισχύει. Η Ευκλείδεια δομή και το UFD είναι υποομάδες της ομάδας των ακεραίων που ανα δύο έχουν μέγιστο κοινό διαρέτη , ομάδες στις οποίες ο μέγιστος κοινός διαιρέτης δύο αριθμών υπάρχει πάντα. Με άλλα λόγια, ένας μέγιστος κοινός διαιρέτης μπορεί να υπάρχει (για όλα τα ζεύγη των στοιχείων μιας ομάδας), αν και μπορεί να μην είναι δυνατόν να βρεθεί χρησιμοποιώντας ένα Ευκλείδειο αλγόριθμο. Μια Ευκλείδεια δομή είναι πάντα μια ομάδα principal ideal domain (PID), μια ακεραία περιοχή στην οποία το μοναδιαίο στοιχείο του δακτυλίου είναι μοναδικό . Και πάλι, το αντίστροφο δεν ισχύει: δεν είναι κάθε PID είναι μια Ευκλείδεια δομή.
Η μοναδική παραγοντοποίηση της Ευκλείδειας δομής είναι χρήσιμη σε πολλές εφαρμογές. Για παράδειγμα, η μοναδική παραγοντοποίηση των ακεραίων Gaussian είναι χρήσιμη στο να προκύπτουν τύποι για όλες τις πυθαγόρειες τριάδες και οδηγεί στην απόδειξη του θεώρηματος του Φερμά για το άθροισμα των τετραγώνων δύο αριθμών . .[114] Η μοναδική παραγοντοποίηση ήταν επίσης ένα βασικό στοιχείο σε μια απόπειρα απόδειξης του Τελευταίου Θεωρήματος του Φερμά Fermat's Last Theorem που δημοσιεύθηκε το 1847 από τον Gabriel Lamé, ο ίδιος μαθηματικός ο οποίος ανέλυσε την αποτελεσματικότητα του αλγορίθμου του Ευκλείδη, που βασίζεται σε πρόταση του Joseph Liouville.[117] η προσέγγιση Lamé απαιτούσε τη μοναδική παραγοντοποίηση των αριθμών της μορφής "x" + ω"y" , όπου "x" και "y" είναι ακέραιοι, και ω = e2iπ/n είναι "n" ρίζα της μονάδας, δηλαδή, ωn = 1. Αν και αυτή η προσέγγιση ισχύει για ορισμένες τιμές των "n" (όπως το "n" = 3, τους ακέραιους Eisenstein), σε γενικές γραμμές τέτοιοι αριθμοί δεν παραγοντοποιούνται μοναδικά. Αυτή η αποτυχία της μοναδικής παραγοντοποίησης στους τομείς cyclotomic field οδήγησε τον Ernst Kummer στην σύλληψη των ideal numbers και, αργότερα,τον Richard Dedekind στην θεωρία των ιδανικών.[εκκρεμεί παραπομπή]
Μοναδική παραγοντοποίηση των τετραγωνικών ακεραίων[Επεξεργασία | επεξεργασία κώδικα]

Οι τετραγωνικοί ακέραιοι δακτυλίοι είναι χρήσιμοι στις Ευκλείδειες δομές.Οι τετραγωνικοί ακέραιοι αποτελούν γενικευση των Gaussian ακεραίων στις οποίες το φανταστικό i αντικαθίσταται από ένα ω αριθμό. Έτσι, έχουν τη μορφή "u" + "v" ω, όπου "υ" και "ν" είναι ακέραιοι και ω έχει μία από τις δύο μορφές, ανάλογα με την παράμετρο "D" . Εάν "D" δεν ισούται με ένα πολλαπλάσιο του τέσσερα συν ένα, τότε
- ω = √D.
Εάν, ωστόσο, D είναι ίσο με ένα πολλαπλάσιο του τέσσερα συν ένα, τότε
- ω = (1 + √D)/2.
Αν η συνάρτηση f αντιστοιχεί σε μια norm συνάρτηση, όπως αυτή που χρησιμοποιείται για να διατάξει τους Gaussian ακέραιους above, τότε η δομή είναι γνωστή ως κανόνας-Ευκλείδη( norm-Euclidean). Οι norm-euclidean τετραγωνικοί ακέραιοι δακτύλιοι είναι ακριβώς εκείνοι όπου D = -11, -7, -3, -2, -1, 2, 3, 5, 6, 7, 11, 13, 17, 19, 21, 29 , 33, 37, 41, 57 ή 73 .[20][118] Οι τετραγωνικοί ακέραιοι με D = -1 και -3 είναι γνωστοί ως Gaussian ακέραιοι και Eisenstein ακέραιοι αντίστοιχα.
Αν f επιτρέπεται να είναι οποιαδήποτε Ευκλείδεια συνάρτηση, τότε οι πιθανές τιμές του D για τις οποίες η δομή είναι Ευκλείδεια δεν είναι ακόμη γνωστοί.[119] Το πρώτο παράδειγμα μιας Ευκλείδειας δομής που δεν ήταν κανόνας-Ευκλείδη (με D = 69) δημοσιεύθηκε το 1994.[119] Το 1973,ο Weinberger απέδειξε ότι ένας τετραγωνικός ακέραιος δακτύλιος με D > 0 είναι Ευκλείδειος αν, και μόνο αν, είναι principal ideal domain, υπό την προϋπόθεση ότι η γενικευμένη υπόθεση Riemann κατέχει..[120]
Μη αντιμεταθετικοί δακύλιοι[Επεξεργασία | επεξεργασία κώδικα]
Είναι επίσης δυνατό να εφαρμοστεί ο Ευκλείδειος αλγόριθμος για μη αντιμεταθετικούς δακτυλίους όπως το σύνολο των Hurwitz quaternions .[121] Έστω α και β αντιπροσωπεύουν δύο στοιχεία από ένα τέτοιο δακτύλιο. Έχουν ένα κοινό δεξί διαιρέτη δ, αν α = ξδ και β = ηδ για κάποια επιλογή του ξ και η στο δακτυλίο. Ομοίως, έχουν ένα κοινό αριστερό διαιρέτη εάν α = δξ και β = δη για κάποια επιλογή του ξ και η στον δακτύλιο. μιας και ο πολλαπλασιασμός δεν είναι αντιμεταθετικός, υπάρχουν δύο εκδοχές του ευκλείδειου αλγόριθμου, μία για τους δεξιούς διαιρέτες και μία για τους αριστερούς διαιρέτες. Η επιλογή των σωστών διαιρέτων, πρώτο βήμα στην εύρεση του ΜΚΔ (α, β) από τον Ευκλείδειο αλγόριθμο, μπορεί να γραφτεί
- ρ0 = α − ψ0β = (ξ − ψ0η)δ
όπου ψ0 αντιπροσωπεύει το πηλίκο και το ρ0 το υπόλοιπο. Αυτή η εξίσωση δείχνει ότι κάθε κοινός δεξιός διαιρέτης των α και β είναι επίσης κοινός διαιρέτης του υπολοίπου ρ0 . Η ανάλογη εξίσωση για τους αριστερούς διαιρέτες θα ήταν
- ρ0 = α − βψ0 = δ(ξ − ηψ0)
Με οποιαδήποτε επιλογή, η διαδικασία επαναλαμβάνεται όπως παραπάνω έως ότου ο μεγαλύτερος κοινός δεξιός ή αριστερός διαιρέτης έχει βρεθεί. Όπως και στην Ευκλείδεια δομή, το "μέγεθος" του ρ0 πρέπει να είναι αυστηρά μικρότερο από β, και πρέπει να υπάρχει μόνο ένας πεπερασμένος αριθμός πιθανών μεγεθών για ρ0 , έτσι ώστε ο αλγόριθμος να τερματίσει σίγουρα.
Τα περισσότερα από τα αποτελέσματα για το ΜΚΔ μεταφέρονται στους μη αντιμεταθετικούς αριθμούς. Για παράδειγμα, η ταυτότητα του Bézout δηλώνει ότι ο δεξιός ΜΚΔ(α, β) μπορεί να εκφραστεί ως γραμμικός συνδυασμός των α και β.Με άλλα λόγια, υπάρχουν σ και τ τέτοια ώστε
- Γright = σα + τβ
Η ανάλογη ταυτότητα για τον αριστερό ΜΚΔ είναι σχεδόν η ίδια
- Γleft = ασ + βτ
Η ταυτότητα του Bézout μπορεί να χρησιμοποιηθεί για την επίλυση διοφαντικών εξισώσεων.
Γενίκευση σε άλλες μαθηματικές δομές[Επεξεργασία | επεξεργασία κώδικα]

Ο Ευκλείδειος αλγόριθμος έχει τρία γενικά χαρακτηριστικά που εξασφαλίζουν από κοινού ότι δεν θα συνεχιστεί επ 'αόριστον. Πρώτον, αυτό μπορεί να γραφτεί ως μια ακολουθία των αναδρομικών εξισώσεων
- rk = rk−2 − qk rk−1
όπου κάθε υπόλοιπο είναι αυστηρά μικρότερο από το προηγούμενο του, |rk| < |rk−1|. Δεύτερον, το μέγεθος του κάθε υπολοίπου έχει ένα ελάχιστο κατώτερο όριο, όπως στα |rk| ≥ 0. . Τρίτον, υπάρχει μόνο ένας πεπερασμένος αριθμός μεγεθών μικρότερων από ένα συγκεκριμένο υπόλοιπο |rk|. Οι γενικεύσεις του αλγορίθμου του Ευκλείδη με αυτά τα βασικά χαρακτηριστικά έχουν εφαρμοστεί σε άλλες μαθηματικές δομές, όπως tangles[123] και στα transfinite ordinal numbers.[124]
Μια σημαντική γενίκευση του ευκλείδειου αλγόριθμου είναι η έννοια της Gröbner basis στην αλγεβρική γεωμετρία . Όπως φαίνεται από τα παραπάνω, ο ΜΚΔ g δύο ακεραίων a και b δημιουργεί τον ιδανικό τους . Με άλλα λόγια, για κάθε επιλογή των ακεραίων s και t , υπάρχει ένα άλλος ακέραιος m τέτοιος ώστε
- sa + tb = mg.
Αν και αυτό εξακολουθεί να ισχύει όταν s , t , m , α και b αντιπροσωπεύουν πολυώνυμα μιας μεταβλητής, δεν ισχύει για τους δακτυλίους με περισσότερες από μία μεταβλητές.[125] Στην περίπτωση αυτή, ένα πεπερασμένο σύνολο των πολυωνύμων g1, g2 , κλπ. μπορεί να οριστεί έτσι ώστε κάθε γραμμικός συνδυασμός των δύο πολυωνύμων πολλών μεταβλητών α και β μπορεί να εκφράζεται ως πολλαπλάσια των γεννητριών
- sa + tb = Σk mkgk
όπου s, t και mk είναι πολυώνυμα πολλών μεταβλητών.[126] Κάθε τέτοιο πολυώνυμο πολυμεταβλητών η f μπορεί να εκφραστεί ως ένα τέτοιο άθροισμα των γενεσιουργών πολυωνύμων συν ένα μοναδικό πολυώνυμο-υπόλοιπο R ,που μερικές φορές ονομάζεται η κανονική μορφή του πολυωνύμου f
- f = r + Σk qkgk
παρόλο που το πολυώνυμο πηλίκο qk μπορεί να μην είναι μοναδικό.[127] The set of these generator polynomials is known as a Gröbner basis.[128] Το σύνολο αυτών των γενεσιουργών πολυωνύμων είναι γνωστό ως βάση.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Thomas L. Heath, The Thirteen Books of Euclid's Elements, 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925], 1956, Dover Publications
- ↑ Toussaint, Godfried (July 31 to August 3, 2005), «The Euclidean algorithm generates traditional musical rhythms», Proceedings of BRIDGES: Mathematical Connections in Art, Music, and Science (Banff, Alberta, Canada): 47–56, http://cgm.cs.mcgill.ca/~godfried/publications/banff.pdf
- ↑ Stark 1978, σελ. 16
- ↑ Stark 1978, σελ. 21
- ↑ LeVeque 1996, σελ. 32
- ↑ LeVeque 1996, σελ. 31
- ↑ Grossman JW (1990). Discrete Mathematics. New York: Macmillan. σελ. 213. ISBN 0-02-348331-8.
- ↑ 8,0 8,1 Schroeder 2005, σελίδες 21–22
- ↑ Schroeder 2005, σελ. 19
- ↑ Ogilvy CS, Anderson JT (1966). Excursions in number theory. New York: Oxford University Press. σελίδες 27–29.
- ↑ 11,0 11,1 Schroeder 2005, σελίδες 216–219
- ↑ 12,0 12,1 LeVeque 1996, σελ. 33
- ↑ Stark 1978, σελ. 25
- ↑ Ore 1948, σελίδες 47–48
- ↑ Stark 1978 , p. 18
- ↑ Stark 1978 , σελ. 16-20
- ↑ Knuth, p. 320.
- ↑ Lovász L, η Pelikan J, Vesztergombi K (2003) Διακριτά Μαθηματικά: Δημοτικό και πέρα . New York: Springer-Verlag. σελ. 100-101. ISBN 0-387-95584-4 .
- ↑ Kimberling C (1983). «A Visual Euclidean Algorithm». Mathematics Teacher 76: 108–109. https://archive.org/details/sim_mathematics-teacher_1983-02_76_2/page/108.
- ↑ 20,0 20,1 Cohn 1962, σελίδες 104–110
- ↑ Knuth, pp. 319–320.
- ↑ Knuth, pp. 318–319.
- ↑ Stillwell 1997, σελ. 14
- ↑ 24,0 24,1 Ore 1948, σελ. 43
- ↑ 25,0 25,1 Stewart BM (1964). Theory of Numbers (2nd έκδοση). New York: Macmillan. σελίδες 43–44.
- ↑ 26,0 26,1 Knuth, p. 318.
- ↑ 27,0 27,1 Weil A (1983). Number Theory. Boston: Birkhäuser. σελίδες 4–6. ISBN 0-8176-3141-0.
- ↑ Jones A (1994). «Greek mathematics to AD 300». Companion encyclopedia of the history and philosophy of the mathematical sciences. New York: Routledge. σελίδες 46–48. ISBN 0-415-09238-8.
- ↑ van der Waerden BL (1954). Science Awakening. translated by Arnold Dresden. Groningen: P. Noordhoff Ltd. σελίδες 114–115.
- ↑ von Fritz K (1945). «The Discovery of Incommensurability by Hippasus of Metapontum». Ann. Math. 46 (2): 242–264. doi:. https://archive.org/details/sim_annals-of-mathematics_1945-04_46_2/page/242.
- ↑ Heath TL (1949). Mathematics in Aristotle. Oxford Press. σελίδες 80–83.
- ↑ Fowler DH (1987). The Mathematics of Plato's Academy: A New Reconstruction. Oxford: Oxford University Press. σελίδες 31–66. ISBN 0-19-853912-6.
- ↑ Becker Ο (1933). «Eudoxus-Studien I. Eine voreuklidische Proportionslehre und ihre Spuren bei Aristoteles und Euklid». Quellen und Studien zur Geschichte der Mathematik B 2: 311–333.
- ↑ 34,0 34,1 Stillwell 1997, σελ. 31
- ↑ 35,0 35,1 Tattersall 2005, σελ. 70
- ↑ Rosen 2000, σελίδες 86–87
- ↑ Ore 1948, σελίδες 247–248
- ↑ Tattersall 2005, σελίδες 72, 184–185
- ↑ Tattersall 2005, σελίδες 72–76
- ↑ 40,0 40,1 Gauss CF (1832). «Theoria residuorum biquadraticorum». Comm. Soc. Reg. Sci. Gött. Rec. 4. See also Werke, 2:67–148.
- ↑ Stillwell 1997, σελίδες 31–32
- ↑ Dirichlet 1894, σελίδες 29–31
- ↑ Richard Dedekind in Dirichlet 1894, Supplement XI
- ↑ Stillwell 2003, σελίδες 41–42
- ↑ Sturm C (1829). «Mémoire sur la résolution des équations numériques». Bull. des sciences de Férussac 11: 419–422.
- ↑ Weisstein, Eric W., "Integer Relation" από το MathWorld.
- ↑ Peterson I (12 August 2002). «Jazzing Up Euclid's Algorithm». ScienceNews. http://www.sciencenews.org/view/generic/id/172/title/Math_Trek__Jazzing_Up_Euclids_Algorithm.
- ↑ Cipra BA (16 May 2000). «The Best of the 20th Century: Editors Name Top 10 Algorithms». SIAM News (Society for Industrial and Applied Mathematics) 33 (4). Αρχειοθετήθηκε από το πρωτότυπο στις 2009-04-07. https://web.archive.org/web/20090407080904/http://amath.colorado.edu/resources/archive/topten.pdf. Ανακτήθηκε στις 2013-06-07.
- ↑ Cole AJ, Davie AJT (1969). «A game based on the Euclidean algorithm and a winning strategy for it». Math. Gaz. 53 (386): 354–357. doi:. https://archive.org/details/sim_mathematical-gazette_1969-12_53_386/page/354.
- ↑ Spitznagel EL (1973). «Properties of a game based on Euclid's algorithm». Math. Mag. 46 (2): 87–92. doi:.
- ↑ Rosen 2000, σελ. 95
- ↑ Roberts J (1977). Elementary Number Theory: A Problem Oriented Approach
 . Cambridge, MA: MIT Press. σελίδες 1–8. ISBN 0-262-68028-9.
. Cambridge, MA: MIT Press. σελίδες 1–8. ISBN 0-262-68028-9.
- ↑ Jones GA, Jones JM (1998). «Bezout's Identity». Elementary Number Theory. New York: Springer-Verlag. σελίδες 7–11.
- ↑ Rosen 2000, σελ. 81
- ↑ Cohn 1962, σελ. 104
- ↑ Rosen 2000, σελ. 91
- ↑ Schroeder 2005, σελ. 23
- ↑ Stark 1978 , σελ. 26-36
- ↑ 59,0 59,1 α β Ore 1948 , p. 44
- ↑ Stark 1978 , σελ. 281-292
- ↑ Rosen 2000 , σελ. 119-125
- ↑ Schroeder 2005 , σελ. 106-107
- ↑ Schroeder 2005 , σελ. 108-109
- ↑ Rosen 2000 , σελ. 120-121
- ↑ Stark 1978 , p. 47
- ↑ Schroeder 2005 , σελ. 107-109
- ↑ Stillwell 1997 , σελ. 186-187
- ↑ Schroeder 2005 , p. 134
- ↑ "κωδικοποίηση διόρθωσης σφάλματος: μαθηματικές μέθοδοι και αλγόριθμοι", σελ. 266, Todd Κ. Moon, John Wiley and Sons, 2005, ISBN 0-471-64800-0
- ↑ Rosen 2000 , σελ. 143-170
- ↑ Schroeder 2005 , σελ. 194-195
- ↑ Vinogradov IM (1954). Στοιχεία Θεωρίας Αριθμών . Νέα Υόρκη: Ντόβερ. σελ. 3-13.
- ↑ Crandall R, Pomerance C (2001). Prime Numbers: μια υπολογιστική προοπτικές (1η έκδοση.). New York: Springer-Verlag. σελ. 225-349. ISBN 0-387-94777-9 .
- ↑ Knuth, σελ. 369-371
- ↑ Shor PW (1997). "Αλγόριθμοι πολυωνυμικού χρόνου για την παραγοντοποίηση και Διαφορετικοί λογάριθμοι σε ένα κβαντικό υπολογιστή". SIAM Journal για την επιστημονική και στατιστική Computing 26 : 1484.
- ↑ Dixon JD (1981). "Ασυμπτωτικά γρήγορη παραγοντοποίηση των ακεραίων". Math.Ηλεκτρονικών υπολογιστών. 36 (153): 255-260. doi : 10.2307/2007743 . JSTOR 2007743 .
- ↑ Lenstra νεώτερος HW (1987). "Ακέραιοι Factoring με ελλειπτικές καμπύλες." Annals of Μαθηματικών 126 (3): 649-673. doi : 10.2307/1971363 . JSTOR 1971363 .
- ↑ Knuth, σελ. 380-384.
- ↑ Knuth, σελ. 339 - 364.
- ↑ Reynaud A.-A.-L. (1811). Traité d'arithmétique à l'χρήσης des élèves qui se destinent à l'École Polytechnique . Courcier.
- ↑ Finck P.-J.-E. (1841). Traité élémentaire d'arithmétique à l'χρήσης des candidats aux SPECIALES écoles . Derivaux.
- ↑ Shallit J (1994). "Προέλευση της ανάλυσης του Ευκλείδειος αλγόριθμος". Math Historia. 21 : 401 - 419.
- ↑ Lamé G (1844). "Note sur la limite du Nombre des τμήματα dans la recherche du plus grand commun diviseur entre deux nombres entiers". Comptes Rendus Ακαδ. . Sci 19 : 867-870.
- ↑ Η Grossman (1924). "Με τον αριθμό των υποδιαιρέσεων στην εύρεση ενός ΠΔΠ". The American Mathematical Monthly 31 (9): 443. doi : 10.2307/2298146 . JSTOR 2298146 .
- ↑ Honsberger R (1976). Μαθηματική Gems II . Η Μαθηματική Association of America . σελ. 54-57. ISBN 0-88385-302-7 .
- ↑ 86,0 86,1 α β γ Knuth, p. 344.
- ↑ Ore 1948 , p. 45
- ↑ 88,0 88,1 α β Knuth, p. 343.
- ↑ Mollin 2008 , p. 21
- ↑ Lévêque 1996 , p. 35
- ↑ Mollin 2008 , σελ. 21-22
- ↑ Knuth, pp. 257–261.
- ↑ Knuth, p. 352.
- ↑ Wagon S (1999). Mathematica in Action. New York: Springer-Verlag. σελίδες 335–336. ISBN 0-387-98252-3.
- ↑ Cohen 1993, σελ. 14
- ↑ Cohen 1993, σελίδες 14–15, 17–18
- ↑ Knuth, pp. 321–323.
- ↑ Stein J (1967). «Computational problems associated with Racah algebra». Journal of Computational Physics 1 (3): 397–405. doi:.
- ↑ 99,0 99,1 Crandall R, Pomerance C (2001). Prime Numbers: A Computational Perspective (1st έκδοση). New York: Springer-Verlag. σελίδες 77–79, 81–85, 425–431. ISBN 0-387-94777-9.
- ↑ Knuth, p. 328.
- ↑ Lehmer DH (1938). «Euclid's Algorithm for Large Numbers». The American Mathematical Monthly 45 (4): 227–233. doi:.
- ↑ Sorenson J (1994). «Two fast GCD algorithms». J. Algorithms 16: 110–144. doi:.
- ↑ Weber K (1995). «The accelerated GCD algorithm». ACM Trans. Math. Soft. 21: 111–122. doi:.
- ↑ Aho A, Hopcroft J· Ullman J (1974). The Design and Analysis of Computer Algorithms
 . New York: Addison–Wesley. σελίδες 300–310. ISBN 0-201-00029-6.
. New York: Addison–Wesley. σελίδες 300–310. ISBN 0-201-00029-6.
- ↑ Schönhage A (1971). «Schnelle Berechnung von Kettenbruchentwicklungen». Acta Informatica 1 (2): 139–144. doi:.
- ↑ Cesari G (1998). «Parallel implementation of Schönhage's integer GCD algorithm». Στο: G. Buhler. Algorithmic Number Theory: Proc. ANTS-III, Portland, OR. New York: Springer-Verlag. σελίδες 64–76. Volume 1423 in Lecture notes in Computer Science.
- ↑ Stehlé D, Zimmermann P (2005). «Gal's accurate tables method revisited». Proceedings of the 17th IEEE Symposium on Computer Arithmetic (ARITH-17). Los Alamitos, CA: IEEE Computer Society Press.
- ↑ Möller N (2008). «On Schönhage's algorithm and subquadratic integer gcd computation». Mathematics of Computation 77 (261): 589–607. doi:. http://www.lysator.liu.se/~nisse/archive/sgcd.pdf.
- ↑ Boyer CB, Merzbach UC (1991). A History of Mathematics
 (2nd έκδοση). New York: Wiley. σελίδες 116–117. ISBN 0-471-54397-7.
(2nd έκδοση). New York: Wiley. σελίδες 116–117. ISBN 0-471-54397-7.
- ↑ Cajori F (1894). A History of Mathematics. New York: Macmillan. σελ. 70. ISBN 0-486-43874-0.
- ↑ Lang S (1984). Algebra (2nd έκδοση). Menlo Park, CA: Addison–Wesley. σελίδες 190–194. ISBN 0-201-05487-6.
- ↑ Cox, Little & O'Shea 1997, σελίδες 37–46
- ↑ Schroeder 2005, σελίδες 254–259
- ↑ 114,0 114,1 114,2 Stillwell 2003, σελίδες 101–116
- ↑ Stark 1978, σελ. 290
- ↑ Cohn 1962, σελίδες 104–105
- ↑ Lamé G (1847). «Mémoire sur la résolution, en nombres complexes, de l'équation An + Bn + Cn = 0». J. Math. Pures Appl. 12: 172–184.
- ↑ LeVeque, William J. (2002) [1956]. Topics in Number Theory, Volumes I and II. New York: Dover Publications. σελίδες II:57,81. ISBN 978-0-486-42539-9. Zbl 1009.11001.
- ↑ 119,0 119,1 Clark, David A. (1994). «A quadratic field which is Euclidean but not norm-Euclidean». Manuscripta Mathematica 83: 327–330. doi:. Zbl 0817.11047. http://www.springerlink.com/content/6t9u2440402n1346/.[νεκρός σύνδεσμος]
- ↑ Weinberger P. On Euclidean rings of algebraic integers. . Proc. Sympos. Pure Math. 24: 321–332.
- ↑ Stillwell 2003, σελίδες 151–152
- ↑ Yamada Y (2007). «Generalized rational blow-down, torus knots, and Euclidean algorithm». arXiv:0708.2316 [math.GT].
- ↑ Conway, John (1970). «An enumeration of knots and links, and some of their algebraic properties». Computational Problems in Abstract Algebra (Proc. Conf., Oxford, 1967). Pergamon. σελίδες 329–358.
- ↑ Jategaonkar AV (1969). «Rings with transfinite left division algorithm». Bull. Amer. Math. Soc. 75 (3): 559–561. doi:. http://projecteuclid.org/euclid.bams/1183530557.
- ↑ Cox, Little & O'Shea 1997, σελ. 65
- ↑ Cox, Little & O'Shea 1997, σελίδες 73–79
- ↑ Cox, Little & O'Shea 1997, σελίδες 79–86
- ↑ Cox, Little & O'Shea 1997, σελ. 74
Βιβλιογραφία[Επεξεργασία | επεξεργασία κώδικα]
- Cohen, Henri (1993). A Course in Computational Algebraic Number Theory. New York: Springer-Verlag. ISBN 0-387-55640-0.
- Cohn, H. (1962). Advanced Number Theory. New York: Dover. ISBN 0-486-64023-X.
- Cormen TH, Rivest RL· Leiserson CE, Stein C (2001). Introduction to Algorithms (2nd έκδοση). MIT Press and McGraw–Hill. ISBN 0-262-03293-7.
- Cox, D· Little, J· O'Shea, D (1997). Ideals, Varieties, and Algorithms: An Introduction to Computational Algebraic Geometry and Commutative Algebra (2nd έκδοση). Springer-Verlag. ISBN 0-387-94680-2.
- Lejeune Dirichlet, Peter Gustav (1894). Dedekind, Richard, επιμ. Vorlesungen über Zahlentheorie (Lectures on Number Theory) (στα Γερμανικά). Braunschweig: Vieweg. LCCN 03005859. OCLC 490186017.
- Hardy GH, Wright EM [revised by D.R. Heath-Brown and J.H. Silverman]. (2008). An Introduction to the Theory of Numbers (6th έκδοση). Oxford: Clarendon Press. ISBN 978-0-19-921986-5.
- Knuth D (1997). The Art of Computer Programming, Volume 2: Seminumerical Algorithms (3rd έκδοση). Addison–Wesley. ISBN 0-201-89684-2.
- LeVeque, William J. (1996) [1977]. Fundamentals of Number Theory. New York: Dover. ISBN 0-486-68906-9.
- Mollin, R. A. (2008). Fundamental Number Theory with Applications (2nd έκδοση). Boca Raton: Chapman & Hall/CRC. ISBN 978-1-4200-6659-3.
- Ore, Øystein (1948). Number Theory and Its History. New York: McGraw–Hill.
- Rosen, K. H. (2000). Elementary Number Theory and its Applications (4th έκδοση). Reading, MA: Addison–Wesley. ISBN 0-201-87073-8.
- Schroeder, Manfred (2005). Number Theory in Science and Communication (4th έκδοση). Springer-Verlag. ISBN 0-387-15800-6.
- Stark, Harold (1978). An Introduction to Number Theory
 . MIT Press. ISBN 0-262-69060-8.
. MIT Press. ISBN 0-262-69060-8. - Stillwell, John (1997). Numbers and Geometry. New York: Springer-Verlag. ISBN 0-387-98289-2.
- Stillwell, John (2003). Elements of Number Theory. New York: Springer-Verlag. ISBN 0-387-95587-9.
- Tattersall, J. J. (2005). Elementary number theory in nine chapters. Cambridge: Cambridge University Press. ISBN 978-0-521-85014-8.
- Uspensky JV, Heaslet MA (1939). Elementary Number Theory. New York: McGraw–Hill.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Demonstrations of Euclid's algorithm
- Weisstein, Eric W., "Euclidean Algorithm" από το MathWorld.
- Euclid's Algorithm at cut-the-knot
- The Euclidean Algorithm at MathPages
- Euclid's Game at cut-the-knot
- Music and Euclid's algorithm









![{\displaystyle {\frac {a}{b}}=q_{0}+{\cfrac {1}{q_{1}+{\cfrac {1}{q_{2}+{\cfrac {1}{\ddots +{\cfrac {1}{q_{N}}}}}}}}}=[q_{0};q_{1},q_{2},\ldots ,q_{N}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae99fb7b3e5da350f429e339994c542c14bac614)
![{\displaystyle {\frac {1071}{462}}=2+{\cfrac {1}{3+{\cfrac {1}{7}}}}=[2;3,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bb1b741861a853bc9f7bcbcd91315b07ffdac0)


