Περιοδικά σημεία μιγαδικών τετραγωνικών απεικονίσεων
Αυτό το λήμμα περιγράφει τα περιοδικά σημεία μιγαδικών τετραγωνικών απεικονίσεων σε ορισμένες περιπτώσεις. Μία τετραγωνική απεικόνιση είναι μία απεικόνιση στην οποία η προηγούμενη τιμή αυξάνεται στις δυνάμεις του 1 και του 2 - και μία μιγαδική απεικόνιση είναι μία απεικόνιση στην οποία η μεταβλητή και οι παράμετροι είναι μιγαδικοί αριθμοί. Ένα περιοδικό σημείο σε μία απεικόνιση είναι μία μεταβλητή τιμή που επαναλαμβάνεται μετά από διαστήματα σταθερού μήκους.[1]
Αυτά τα περιοδικά σημεία παίζουν ρόλο στις θεωρίες συνόλων του Φατού και της Julia.
Ορισμοί[Επεξεργασία | επεξεργασία κώδικα]
Έστω
Είναι η μιγαδική τετραγωνική απεικόνιση, όπου και είναι μιγαδικοί αριθμοί.
Συμβολικά, είναι η -πλάσια σύνθεση της με τον εαυτό της (δεν πρέπει να συγχέεται με την -οστή παράγωγος της )-δηλαδή, η τιμή μετά την k-οστή επανάληψη της συνάρτησης Έτσι
Τα περιοδικά σημεία μιας μιγαδικής τετραγωνικής απεικόνισης περιόδου είναι σημεία του δυναμικού επιπέδου τέτοια ώστε
όπου είναι ο μικρότερος θετικός ακέραιος για τον οποίο ισχύει η εξίσωση στο συγκεκριμένο z.
Έτσι μπορούμε να εισάγουμε μια νέα συνάρτηση:
οπότε τα περιοδικά σημεία είναι μηδενικά της συνάρτησης : σημεία z που ικανοποιούν
το οποίο είναι ένα πολυώνυμο βαθμού
Αριθμός περιοδικών σημείων[Επεξεργασία | επεξεργασία κώδικα]
Ο βαθμός του πολυωνύμου που περιγράφει τα περιοδικά σημεία είναι οπότε έχει ακριβώς σύνθετες ρίζες (= περιοδικά σημεία), που μετριούνται με την πολλαπλότητα.
Σταθερότητα περιοδικών σημείων (τροχιά) - πολλαπλασιαστής[Επεξεργασία | επεξεργασία κώδικα]

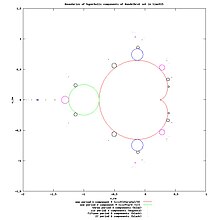

Ο πολλαπλασιαστής (ή ιδιοτιμή, παράγωγος) ενός ορθολογικού χάρτη που επαναλαμβάνεται φορές στο κυκλικό σημείο ορίζεται ως εξής:
όπου είναι η πρώτη παράγωγος του ως προς στο .
Επειδή ο πολλαπλασιαστής είναι ο ίδιος σε όλα τα περιοδικά σημεία μιας δεδομένης τροχιάς, ονομάζεται πολλαπλασιαστής της περιοδικής τροχιάς.
Ο πολλαπλασιαστής είναι:
- ένας μιγαδικός αριθμός,
- αναλλοίωτος κάτω από τη σύζευξη οποιουδήποτε ορθολογικού χάρτη στο σταθερό του σημείο;[2]
- χρησιμοποιείται για τον έλεγχο της ευστάθειας περιοδικών (επίσης σταθερών) σημείων με δείκτη ευστάθειας
Ένα περιοδικό σημείο είναι [3]
- προσελκύει όταν
- υπερ-ελκυστική όταν
- ελκτική αλλά όχι υπερ-ελκυστική όταν
- αδιάφορο όταν
- λογικά αδιάφορη ή παραβολική αν η είναι ρίζα της ενότητας,
- Μη ορθολογικά αδιάφορη αν αλλά ο πολλαπλασιαστής δεν είναι ρίζα της μονάδας,
- απωθείται όταν
Περιοδικά σημεία
- που προσελκύουν είναι πάντα στο σύνολο Φατού,
- που είναι απωθητικά είναι στο σύνολο Julia,
- που είναι αδιάφορα σταθερά σημεία μπορεί να βρίσκονται στο ένα ή στο άλλο.[4] Ένα παραβολικό περιοδικό σημείο βρίσκεται στο σύνολο Julia.
Σημεία περιόδου 1 (σταθερά σημεία)[Επεξεργασία | επεξεργασία κώδικα]
Περιορισμένα σταθερά σημεία[Επεξεργασία | επεξεργασία κώδικα]
Αρχικά, αναζητούμε όλα τα πεπερασμένα σημεία που παραμένουν αμετάβλητα από μία εφαρμογή του . Αυτά είναι τα σημεία που ικανοποιούν το . Δηλαδή, θέλουμε να λύσουμε
η οποία μπορεί να επαναδιατυπωθεί ως εξής
Δεδομένου ότι πρόκειται για μια συνηθισμένη τετραγωνική εξίσωση με έναν άγνωστο, μπορούμε να εφαρμόσουμε τον τυπικό τύπο επίλυσης τετραγωνικής εξίσωσης:
- και
Έτσι για έχουμε δύο πεπερασμένα σταθερά σημεία και .
Δεδομένου ότι το
- και όπου
έχουμε .
Έτσι, τα σταθερά σημεία είναι συμμετρικά ως προς .
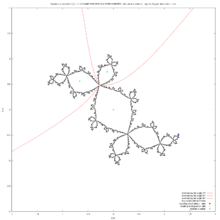
Σύνθετη δυναμική[Επεξεργασία | επεξεργασία κώδικα]


Στην περίπτωση αυτή χρησιμοποιείται συνήθως διαφορετικός συμβολισμός:[5]
- με πολλαπλασιαστή
και
- με πολλαπλασιαστή
Και πάλι έχουμε
Δεδομένου ότι η παράγωγος ως προς το z είναι
έχουμε
Αυτό σημαίνει ότι το μπορεί να έχει το πολύ ένα ελκυστικό σταθερό σημείο.
Τα σημεία αυτά διακρίνονται από τα ακόλουθα:
- είναι:
- το σημείο προσγείωσης της εξωτερικής ακτίνας για γωνία=0 για
- το πιο απωθητικό σταθερό σημείο του συνόλου Julia
- το ένα στα δεξιά (όποτε τα σταθερά σημεία δεν είναι συμμετρικά γύρω από τον πραγματικό άξονα), είναι το ακραίο δεξιό σημείο για τα συνδεδεμένα σύνολα Julia (εκτός από το κουνουπίδι).[6]
- είναι:
- το σημείο προσγείωσης πολλών ακτίνων
- προσέλκυση όταν το βρίσκεται στο κύριο καρδιοειδές του συνόλου Mandelbrot, οπότε βρίσκεται στο εσωτερικό ενός συμπληρωμένου συνόλου Julia και επομένως ανήκει στο σύνολο Φατού (αυστηρά στη λεκάνη έλξης του πεπερασμένου σταθερού σημείου).
- παραβολική στο σημείο της ρίζας του άκρου του συνόλου Μάντελμπροτ
- απωθητική για άλλες τιμές του
Ειδικές περιπτώσεις[Επεξεργασία | επεξεργασία κώδικα]
Μια σημαντική περίπτωση της τετραγωνικής απεικόνισης είναι η . Στην περίπτωση αυτή, έχουμε και . Σε αυτή την περίπτωση, το 0 είναι ένα υπερελκυστικό Σταθερό σημείο και το 1 ανήκει στο σύνολο Julia.
Μόνο ένα σταθερό σημείο[Επεξεργασία | επεξεργασία κώδικα]
Έχουμε ακριβώς όταν Η εξίσωση αυτή έχει μία λύση, οπότε . Στην πραγματικότητα είναι η μεγαλύτερη θετική, καθαρά πραγματική τιμή αριθμού για την οποία υπάρχει πεπερασμένος ελκυστής.
Άπειρο σταθερό σημείο[Επεξεργασία | επεξεργασία κώδικα]
Μπορούμε να επεκτείνουμε το μιγαδικό επίπεδο στη σφαίρα Ρίμαν (εκτεταμένο μιγαδικό επίπεδο) προσθέτοντας σημείο στο άπειρο:
και επέκταση έτσι ώστε
Τότε το σημείο στο άπειρο είναι:
- σούπερ ελκυστικό
- ένα σταθερό σημείο του :[7]
Περίοδος-2 κύκλοι[Επεξεργασία | επεξεργασία κώδικα]


Κύκλοι περιόδου-2 είναι δύο διαφορετικά σημεία και τέτοια ώστε και , και επομένως
για :
Με την εξίσωση του z, προκύπτει
Η εξίσωση αυτή είναι πολυώνυμο 4ου βαθμού και έχει τέσσερις (ενδεχομένως μη διακριτές) λύσεις. Ωστόσο, γνωρίζουμε ήδη δύο από τις λύσεις. Είναι οι και , που υπολογίστηκαν παραπάνω, αφού αν αυτά τα σημεία παραμένουν αμετάβλητα από μία εφαρμογή της , τότε είναι σαφές ότι θα παραμείνουν αμετάβλητα από περισσότερες από μία εφαρμογές της .
Το πολυώνυμό μας 4ης τάξης μπορεί επομένως να παραγοντοποιηθεί με 2 τρόπους:
Πρώτη μέθοδος παραγοντοποίησης[Επεξεργασία | επεξεργασία κώδικα]
Επομένως, αυτό αναπτύσσεται άμεσα ως ( σημειώστε τα εναλλασσόμενα πρόσημα), όπου
Έχουμε ήδη δύο λύσεις και χρειαζόμαστε μόνο τις άλλες δύο. Επομένως, το πρόβλημα είναι ισοδύναμο με την επίλυση ενός τετραγωνικού πολυωνύμου. Ειδικότερα, σημειώστε ότι
και
Προσθέτοντας αυτά στα παραπάνω, έχουμε και . Αντιστοιχίζοντας αυτά με τους συντελεστές από την ανάπτυξη του , έχουμε
- και
Από αυτό, παίρνουμε εύκολα
- και .
Από το σημείο αυτό, κατασκευάζουμε μια τετραγωνική εξίσωση με και εφαρμόζουμε τον τυποποιημένο τύπο λύσης για να πάρουμε
- και
Μια πιο προσεκτική εξέταση δείχνει ότι:
- και
που σημαίνει ότι αυτά τα δύο σημεία είναι τα δύο σημεία ενός ενιαίου κύκλου περιόδου 2.
Δεύτερη μέθοδος παραγοντοποίησης[Επεξεργασία | επεξεργασία κώδικα]
Μπορούμε να παραγοντοποιήσουμε το τεταρτοβάθμιο χρησιμοποιώντας πολυωνυμική μακρά διαίρεση για να διαιρέσουμε τους παράγοντες και οι οποίοι αντιπροσωπεύουν τα δύο σταθερά σημεία και (των οποίων οι τιμές δόθηκαν νωρίτερα και οι οποίες εξακολουθούν να παραμένουν στο σταθερό σημείο μετά από δύο επαναλήψεις):
Οι ρίζες του πρώτου παράγοντα είναι τα δύο σταθερά σημεία. Είναι απωθητικά εκτός της κύριας καρδιοειδούς.
Ο δεύτερος παράγοντας έχει τις δύο ρίζες
Αυτές οι δύο ρίζες, οι οποίες είναι ίδιες με εκείνες που βρέθηκαν με την πρώτη μέθοδο, σχηματίζουν την τροχιά της περιόδου 2.[8]
Ειδικές περιπτώσεις[Επεξεργασία | επεξεργασία κώδικα]
Και πάλι, ας δούμε το . Τότε
- και
και οι δύο είναι μιγαδικοί αριθμοί. Έχουμε . Έτσι, και τα δύο αυτά σημεία "κρύβονται" στο σύνολο Julia. Μια άλλη ειδική περίπτωση είναι η , η οποία δίνει και . Αυτό δίνει τον γνωστό υπερ-ελκυστικό κύκλο που βρίσκεται στο μεγαλύτερο λοβό περιόδου-2 του τετραγωνικού συνόλου Μάντελμπροτ.
Κύκλοι για περίοδο μεγαλύτερη από 2[Επεξεργασία | επεξεργασία κώδικα]

Ο βαθμός της εξίσωσης είναι 2n- επομένως, για να βρούμε τα σημεία σε έναν κύκλο 3 θα πρέπει να λύσουμε μια εξίσωση 8ου βαθμού. Αφού εξαιρέσουμε τους παράγοντες που δίνουν τα δύο σταθερά σημεία, θα είχαμε μια εξίσωση έκτου βαθμού.
Δεν υπάρχει γενική λύση σε ρίζες για πολυωνυμικές εξισώσεις πέντε ή μεγαλύτερου βαθμού, οπότε τα σημεία ενός κύκλου με περίοδο μεγαλύτερη του 2 πρέπει γενικά να υπολογίζονται με αριθμητικές μεθόδους. Ωστόσο, στην ειδική περίπτωση της περιόδου 4 τα σημεία του κύκλου έχουν μακροσκελείς εκφράσεις σε ρίζες[9].
Στην περίπτωση c = -2, υπάρχουν τριγωνομετρικές λύσεις για τα περιοδικά σημεία όλων των περιόδων. Η περίπτωση είναι ισοδύναμη με την περίπτωση της λογιστικής απεικόνισης r = 4: Εδώ η ισοδυναμία δίνεται από τη σχέση Ένας από τους k-κύκλους της λογιστικής μεταβλητής x (όλοι οι κύκλοι της οποίας είναι απωθητικοί) είναι
Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]
- Alan F. Beardon, Iteration of Rational Functions, Springer 1991, (ISBN 0-387-95151-2)
- Michael F. Barnsley (Author), Stephen G. Demko (Editor), Chaotic Dynamics and Fractals (Notes and Reports in Mathematics in Science and Engineering Series) Academic Pr (April 1986), (ISBN 0-12-079060-2)
- Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
- The permutations of periodic points in quadratic polynominials by J Leahy
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Algebraic solution of Mandelbrot orbital boundaries by Donald D. Cross
- Brown Method by Robert P. Munafo
- arXiv:hep-th/0501235v2 V.Dolotin, A.Morozov: Algebraic Geometry of Discrete Dynamics. The case of one variable.
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- Αλγόριθμος διαμαντιού τετραγώνου
- Καμπύλη που γεμίζει το χώρο
- Νιφάδα του Κοχ
- Καμπύλη Χίλμπερτ
- Καμπύλη του δράκου
- Σπόγγος του Μένγκερ
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Alexander, James C. (14 Νοεμβρίου 2006). Dynamical Systems: Proceedings of the Special Year Held at the University of Maryland, College Park, 1986-87. Springer. ISBN 978-3-540-45946-0.
- ↑ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, (ISBN 0-387-95151-2), p. 41
- ↑ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, (ISBN 0-387-95151-2), page 99
- ↑ «Some Julia sets by Michael Becker». Αρχειοθετήθηκε από το πρωτότυπο στις 18 Φεβρουαρίου 2020. Ανακτήθηκε στις 7 Ιανουαρίου 2024.
- ↑ On the regular leaf space of the cauliflower by Tomoki Kawahira Source: Kodai Math. J. Volume 26, Number 2 (2003), 167-178. Αρχειοθετήθηκε 2011-07-17 στο Wayback Machine.
- ↑ Periodic attractor by Evgeny Demidov Αρχειοθετήθηκε 2008-05-11 στο Wayback Machine.
- ↑ R L Devaney, L Keen (Editor): Chaos and Fractals: The Mathematics Behind the Computer Graphics. Publisher: Amer Mathematical Society July 1989, (ISBN 0-8218-0137-6) , (ISBN 978-0-8218-0137-6)
- ↑ Period 2 orbit by Evgeny Demidov Αρχειοθετήθηκε 2008-05-11 στο Wayback Machine.
- ↑ Gvozden Rukavina : Quadratic recurrence equations - exact explicit solution of period four fixed points functions in bifurcation diagram











































































































