Μιγαδικό τετραγωνικό πολυώνυμο

Ένα μιγαδικό τετραγωνικό πολυώνυμο είναι ένα τετραγωνικό πολυώνυμο του οποίου οι συντελεστές και η μεταβλητή είναι μιγαδικοί αριθμοί.

Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]

Τα τετραγωνικά πολυώνυμα έχουν τις ακόλουθες ιδιότητες, ανεξάρτητα από τη μορφή τους:

Είναι μονοκρίσιμο πολυώνυμο, δηλαδή έχει ένα μόνο πεπερασμένο κρίσιμο σημείο στο μιγαδικό επίπεδο. Το δυναμικό επίπεδο αποτελείται από 2 το πολύ λεκάνες: τη λεκάνη του απείρου και τη λεκάνη του πεπερασμένου κρίσιμου σημείου (αν το πεπερασμένο κρίσιμο σημείο δεν διαφεύγει).
Μπορεί να είναι μετα-κριτικά πεπερασμένο, δηλαδή η τροχιά του κρίσιμου σημείου μπορεί να είναι πεπερασμένη, επειδή το κρίσιμο σημείο είναι περιοδικό ή προ-περιοδικό^[1].
Είναι μονότροπη συνάρτηση,
Είναι Ρητή συνάρτηση,
Είναι ολοκληρωμένη συνάρτηση.

Τύποι[Επεξεργασία | επεξεργασία κώδικα]

Όταν το τετραγωνικό πολυώνυμο έχει μόνο μία μεταβλητή (μονομεταβλητό), υπάρχουν τέσσερις κύριες μορφές:

Η γενική μορφή: $f(x)=a_{2}x^{2}+a_{1}x+a_{0}$ όπου $a_{2}\neq 0$
Η παραγοντική μορφή που χρησιμοποιείται για τον λογιστικό χάρτη: $f_{r}(x)=rx(1-x)$
$f_{\theta }(x)=x^{2}+\lambda x$ που έχει αδιάφορο σταθερό σημείο με πολλαπλασιαστή $\lambda =e^{2\pi \theta i}$ στην αφετηρία ^[2]
Το μονικό πολυώνυμο και η κεντροποιημένη μορφή, $f_{c}(x)=x^{2}+c$

Η μονική και κεντραρισμένη μορφή έχει μελετηθεί εκτενώς και έχει τις ακόλουθες ιδιότητες:

Είναι η απλούστερη μορφή μιας μη γραμμικής συνάρτησης με έναν συντελεστή (παράμετρος),
Είναι ένα κεντραρισμένο πολυώνυμο (το άθροισμα των κρίσιμων σημείων του είναι μηδέν).^[3]
Είναι διωνυμικό (πολυώνυμο)

Η μορφή λάμδα $f_{\lambda }(z)=z^{2}+\lambda z$ είναι:

η απλούστερη μη τετριμμένη διαταραχή του αδιατάρακτου συστήματος $z\mapsto \lambda z$
"η πρώτη οικογένεια δυναμικών συστημάτων στην οποία είναι γνωστές ρητές αναγκαίες και ικανές συνθήκες για το πότε ένα πρόβλημα μικρού διαιρέτη είναι σταθερό"^[4]

Συζυγία[Επεξεργασία | επεξεργασία κώδικα]

Μεταξύ σχημάτων[Επεξεργασία | επεξεργασία κώδικα]

Δεδομένου ότι το $f_{c}(x)$ είναι συζυγές με τη γενική μορφή του τετραγωνικού πολυωνύμου χρησιμοποιείται συχνά για τη μελέτη της σύνθετης δυναμικής και για τη δημιουργία εικόνων των συνόλων Μάντελμπροτ, Julia και Φατού.

Εάν επιθυμούμε αλλαγή από $\theta$ σε $c$ :^[2]

c=c(\theta )={\frac {e^{2\pi \theta i}}{2}}\left(1-{\frac {e^{2\pi \theta i}}{2}}\right).

Όταν θέλουμε να μεταβούμε από το $r$ στο $c$ , ο μετασχηματισμός των παραμέτρων είναι^[5]

c=c(r)={\frac {1-(r-1)^{2}}{4}}=-{\frac {r}{2}}\left({\frac {r-2}{2}}\right)

και ο μετασχηματισμός μεταξύ των μεταβλητών στο $z_{t+1}=z_{t}^{2}+c$ και $x_{t+1}=rx_{t}(1-x_{t})$ είναι

z=r\left({\frac {1}{2}}-x\right).

Με διπλασιασμό χάρτη[Επεξεργασία | επεξεργασία κώδικα]

Υπάρχει ημι-συζυγία μεταξύ του δυαδικού μετασχηματισμού (του χάρτη διπλασιασμού) και της τετραγωνικής πολυωνυμικής περίπτωσης του c = –2.

Συμβολισμός[Επεξεργασία | επεξεργασία κώδικα]

Επανάληψη[Επεξεργασία | επεξεργασία κώδικα]

Εδώ $f^{n}$ δηλώνει την n-th επαναλαμβανόμενη τιμή της συνάρτησης $f$ :

f_{c}^{n}(z)=f_{c}^{1}(f_{c}^{n-1}(z))

οπότε

z_{n}=f_{c}^{n}(z_{0}).

Λόγω πιθανής σύγχυσης με την εκθετικοποίηση, ορισμένοι συντάκτες γράφουν $f^{\circ n}$ για την nth επαναλαμβανόμενη επανάληψη της $f$ .

Παράμετρος[Επεξεργασία | επεξεργασία κώδικα]

Η μονική και κεντροποιημένη μορφή $f_{c}(x)=x^{2}+c$ μπορεί να σημειωθεί με:

την παράμετρο $c$
την εξωτερική γωνία $\theta$ $\theta$ της ακτίνας που προσγειώνεται:
- στο c στο σύνολο Μάντελμπροτ του επιπέδου παραμέτρων
- στην κρίσιμη τιμή: z = c στο σύνολο Julia του δυναμικού επιπέδου

οπότε :

f_{c}=f_{\theta }

c=c({\theta })

Παραδείγματα:

Το c είναι το σημείο προσγείωσης της 1/6 εξωτερικής ακτίνας του συνόλου Μάντελμπροτ και είναι $z\to z^{2}+i$ (όπου i^2=-1)
c είναι το σημείο προσγείωσης της 5/14 εξωτερικής ακτίνας και είναι $z\to z^{2}+c$ με $c=-1.23922555538957+0.412602181602004*i$

1/4
1/6
9/56
129/16256

Χάρτης[Επεξεργασία | επεξεργασία κώδικα]

Η μονική και κεντραρισμένη μορφή, που μερικές φορές ονομάζεται οικογένεια τετραγωνικών πολυωνύμων Ντουάντι-Χάμπαρντ,^[6] χρησιμοποιείται συνήθως με μεταβλητή $z$ και παράμετρο $c$ :

f_{c}(z)=z^{2}+c.

Όταν χρησιμοποιείται ως συνάρτηση εξέλιξης του διακριτού μη γραμμικού δυναμικού συστήματος

z_{n+1}=f_{c}(z_{n})

ονομάζεται τετραγωνικός χάρτης:^[7]

f_{c}:z\to z^{2}+c.

Το σύνολο Μάντελμπροτ είναι το σύνολο των τιμών της παραμέτρου c για τις οποίες η αρχική συνθήκη z₀ = 0 δεν προκαλεί απόκλιση των επαναλήψεων στο άπειρο.

Κρίσιμα στοιχεία[Επεξεργασία | επεξεργασία κώδικα]

Κρίσιμα σημεία[Επεξεργασία | επεξεργασία κώδικα]

Σύνθετο επίπεδο[Επεξεργασία | επεξεργασία κώδικα]

Κρίσιμο σημείο της $f_{c}$ είναι ένα σημείο $z_{cr}$ στο δυναμικό επίπεδο τέτοιο ώστε η παράγωγος να εξαφανίζεται:

f_{c}'(z_{cr})=0.

Από το

f_{c}'(z)={\frac {d}{dz}}f_{c}(z)=2z

υποδηλώνει

z_{cr}=0,

διαπιστώνουμε ότι το μοναδικό (πεπερασμένο) κρίσιμο σημείο του $f_{c}$ είναι το σημείο $z_{cr}=0$ .

$z_{0}$ είναι ένα αρχικό σημείο για την επανάληψη του συνόλου Μάντελμπροτ^[8]

Για την τετραγωνική οικογένεια $f_{c}(z)=z^{2}+c$ το κρίσιμο σημείο z=0 είναι το κέντρο συμμετρίας του σύνολο Julia Jc, οπότε είναι ένας κυρτός συνδυασμός δύο σημείων στο Jc.^[9]

Εκτεταμένο μιγαδικό επίπεδο[Επεξεργασία | επεξεργασία κώδικα]

Στη Σφαίρα του Ρίμαν το πολυώνυμο έχει 2d-2 κρίσιμα σημεία. Εδώ το μηδέν και το άπειρο είναι κρίσιμα σημεία.

Κρίσιμη αξία[Επεξεργασία | επεξεργασία κώδικα]

Μια κρίσιμη τιμή $z_{cv}$ της $f_{c}$ είναι η εικόνα ενός κρίσιμου σημείου:

z_{cv}=f_{c}(z_{cr})

Από το

z_{cr}=0

έχουμε

z_{cv}=c

Έτσι, η παράμετρος $c$ είναι η κρίσιμη τιμή της $f_{c}(z)$ .

Καμπύλες κρίσιμου επιπέδου[Επεξεργασία | επεξεργασία κώδικα]

Μια καμπύλη κρίσιμης στάθμης είναι η καμπύλη στάθμης που περιέχει κρίσιμο σημείο. Λειτουργεί ως ένα είδος σκελετού^[10] του δυναμικού επιπέδου.

Παράδειγμα : οι καμπύλες επιπέδων διασταυρώνονται στο σημείο σέλας, το οποίο είναι ένας ειδικός τύπος κρίσιμου σημείου.

προσέλκυση
προσέλκυση
προσέλκυση
παραβολική
Βίντεο για το c κατά μήκος της εσωτερικής ακτίνας 0

Ορισμός κρίσιμου ορίου[Επεξεργασία | επεξεργασία κώδικα]

Το κρίσιμο οριακό σύνολο είναι το σύνολο της εμπρόσθιας τροχιάς όλων των κρίσιμων σημείων

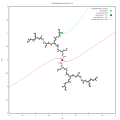
Κρίσιμη τροχιά[Επεξεργασία | επεξεργασία κώδικα]

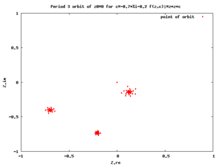
Δυναμικό επίπεδο με σύνολο Julia και κρίσιμη τροχιά.

Δυναμικό επίπεδο : μεταβολές της κρίσιμης τροχιάς κατά μήκος της εσωτερικής ακτίνας της κύριας καρδιοειδούς για γωνία 1/6

Η εμπρόσθια τροχιά ενός κρίσιμου σημείου ονομάζεται κρίσιμη τροχιά. Οι κρίσιμες τροχιές είναι πολύ σημαντικές επειδή κάθε ελκτική περιοδική τροχιά έλκει ένα κρίσιμο σημείο, οπότε η μελέτη των κρίσιμων τροχιών μας βοηθά να κατανοήσουμε τη δυναμική στο σύνολο Φατού.^[11]^[12]^[13]

z_{0}=z_{cr}=0

z_{1}=f_{c}(z_{0})=c

z_{2}=f_{c}(z_{1})=c^{2}+c

z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c

\ \vdots

Αυτή η τροχιά εμπίπτει σε έναν ελκτικό περιοδικό κύκλο, αν υπάρχει.

Κρίσιμος τομέας[Επεξεργασία | επεξεργασία κώδικα]

Ο κρίσιμος τομέας είναι ένας τομέας του δυναμικού επιπέδου που περιέχει το κρίσιμο σημείο.

Κρίσιμο σύνολο[Επεξεργασία | επεξεργασία κώδικα]

Το κρίσιμο σύνολο είναι ένα σύνολο κρίσιμων σημείων

Κριτικό πολυώνυμο[Επεξεργασία | επεξεργασία κώδικα]

P_{n}(c)=f_{c}^{n}(z_{cr})=f_{c}^{n}(0)

οπότε

P_{0}(c)=0

P_{1}(c)=c

P_{2}(c)=c^{2}+c

P_{3}(c)=(c^{2}+c)^{2}+c

Αυτά τα πολυώνυμα χρησιμοποιούνται για:

εύρεση των κέντρων αυτών των συνιστωσών του συνόλου Μάντελμπροτ περιόδου n. Τα κέντρα είναι οι ρίζες των n-th κρίσιμων πολυωνύμων

{\text{centers}}=\{c:P_{n}(c)=0\}

εύρεση ριζών των συνιστωσών του συνόλου Mandelbrot περιόδου n (τοπικό ελάχιστο του $P_{n}(c)$ )
Σημείο Μισιουρέβιτς

M_{n,k}=\{c:P_{k}(c)=P_{k+n}(c)\}

Κρίσιμες καμπύλες[Επεξεργασία | επεξεργασία κώδικα]

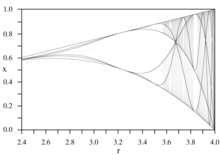
Τα διαγράμματα των κρίσιμων πολυωνύμων ονομάζονται κρίσιμες καμπύλες.^[14]

Αυτές οι καμπύλες δημιουργούν τον σκελετό (οι σκούρες γραμμές) ενός διάγραμμα διακλάδωσης.^[15]^[16]

Χώροι, επίπεδα[Επεξεργασία | επεξεργασία κώδικα]

4Δ χώροι[Επεξεργασία | επεξεργασία κώδικα]

Μπορεί κανείς να χρησιμοποιήσει τον τετραδιάστατο (4D) χώρο Julia-Μάντελμπροτ για μια σφαιρική ανάλυση αυτού του δυναμικού συστήματος.^[17]

Στο χώρο αυτό υπάρχουν δύο βασικοί τύποι 2D επιπέδων:

το δυναμικό (δυναμικό) επίπεδο, $f_{c}$ -επίπεδο ή c'-επίπεδο
το επίπεδο παραμέτρων ή z-επίπεδο

Υπάρχει επίσης ένα άλλο επίπεδο που χρησιμοποιείται για την ανάλυση τέτοιων δυναμικών συστημάτων w-επίπεδο:

το επίπεδο σύζευξης ^[18]
πρότυπο επίπεδο. ^[19]

2Δ Επίπεδο παραμέτρων[Επεξεργασία | επεξεργασία κώδικα]

Parameter plane types
επίπεδο παραμέτρων r (λογιστικός χάρτης)
c επίπεδο παραμέτρων

Ο χώρος φάσεων ενός τετραγωνικού χάρτη ονομάζεται επίπεδο παραμέτρων. Εδώ:

$z_{0}=z_{cr}$ είναι σταθερός και $c$ μεταβλητός.

Δεν υπάρχει δυναμική εδώ. Είναι μόνο ένα σύνολο τιμών παραμέτρων. Δεν υπάρχουν τροχιές στο επίπεδο των παραμέτρων.

Το επίπεδο παραμέτρων αποτελείται από:

Το σύνολο Μάντελμπροτ
- Ο τόπος διακλάδωσης = το όριο του συνόλου Μάντελμπροτ με
  - σημεία ρίζας
- Περιορισμένες υπερβολικές συνιστώσες του συνόλου Μάντελμπροτ = εσωτερικό του συνόλου Μάντελμπροτ^[20]

με εσωτερικές ακτίνες

εξωτερικό του συνόλου Μάντελμπροτ με
- εξωτερικές ακτίνες
- ισοδυναμικές γραμμές

Υπάρχουν πολλοί διαφορετικοί υπότυποι του επιπέδου παραμέτρων.^[21]^[22]

Δείτε επίσης :

Χάρτης Μπότσερ που απεικονίζει το εξωτερικό του συνόλου Μάντελμπροτ στο εξωτερικό του μοναδιαίου δίσκου
πολλαπλασιαστικός χάρτης που αντιστοιχίζει το εσωτερικό της υπερβολικής συνιστώσας του συνόλου Μάντελμπροτ στο εσωτερικό του μοναδιαίου δίσκου

2Δ Δυναμικό επίπεδο[Επεξεργασία | επεξεργασία κώδικα]

"Το πολυώνυμο Pc απεικονίζει κάθε δυναμική ακτίνα σε μια άλλη ακτίνα που διπλασιάζει τη γωνία (την οποία μετράμε σε πλήρεις στροφές, δηλαδή 0 = 1 = 2π rad = 360°), και οι δυναμικές ακτίνες οποιουδήποτε πολυωνύμου "μοιάζουν με ευθείες ακτίνες" κοντά στο άπειρο. Αυτό μας επιτρέπει να μελετήσουμε συνδυαστικά τα σύνολα Μάντελμπροτ και Julia, αντικαθιστώντας το δυναμικό επίπεδο με τον μοναδιαίο κύκλο, τις ακτίνες με γωνίες και το τετραγωνικό πολυώνυμο με τον χάρτη διπλασιασμού modulo one". Virpi Kauko^[23]

Στο δυναμικό επίπεδο μπορεί κανείς να βρει:

Το σύνολο Julia
Το Γεμισμένο σύνολο Julia
Το σύνολο Φατού
Τροχιές

Το δυναμικό επίπεδο αποτελείται από:

Εδώ, $c$ είναι μια σταθερά και $z$ είναι μια μεταβλητή.

Το δισδιάστατο δυναμικό επίπεδο μπορεί να αντιμετωπιστεί ως τομή Πουανκαρέ του τρισδιάστατου χώρου του συνεχούς δυναμικού συστήματος.^[24]^[25]

Τα δυναμικά z-επίπεδα μπορούν να χωριστούν σε δύο ομάδες:

$f_{0}$ επίπεδο για $c=0$ (βλ. μιγαδικός χάρτης τετραγωνισμού)
$f_{c}$ επίπεδα (όλα τα άλλα επίπεδα για $c\neq 0$ )

Σφαίρα Ρίμαν[Επεξεργασία | επεξεργασία κώδικα]

Το εκτεταμένο μιγαδικό επίπεδο συν ένα σημείο στο άπειρο

η σφαίρα Ρίμαν

Παράγωγα[Επεξεργασία | επεξεργασία κώδικα]

Πρώτη παράγωγος ως προς c[Επεξεργασία | επεξεργασία κώδικα]

Στο επίπεδο των παραμέτρων:

$c$ είναι μια μεταβλητή
$z_{0}=0$ είναι σταθερά

Η πρώτη παράγωγος του $f_{c}^{n}(z_{0})$ ως προς c είναι

z_{n}'={\frac {d}{dc}}f_{c}^{n}(z_{0}).

Αυτή η παράγωγος μπορεί να βρεθεί με επανάληψη ξεκινώντας με

z_{0}'={\frac {d}{dc}}f_{c}^{0}(z_{0})=1

και στη συνέχεια αντικαθιστώντας σε κάθε διαδοχικό βήμα

z_{n+1}'={\frac {d}{dc}}f_{c}^{n+1}(z_{0})=2\cdot {}f_{c}^{n}(z)\cdot {\frac {d}{dc}}f_{c}^{n}(z_{0})+1=2\cdot z_{n}\cdot z_{n}'+1.

Αυτό μπορεί εύκολα να επαληθευτεί χρησιμοποιώντας τον κανόνα της αλυσίδας για την παράγωγο.

Αυτή η παράγωγος χρησιμοποιείται στη μέθοδο εκτίμησης απόστασης για τη σχεδίαση ενός συνόλου Μάντελμπροτ.

Πρώτη παράγωγος ως προς z[Επεξεργασία | επεξεργασία κώδικα]

Στο δυναμικό επίπεδο:

$z$ είναι μια μεταβλητή,
$c$ είναι μια σταθερά.

Σε ένα σταθερό σημείο $z_{0}$ ,

f_{c}'(z_{0})={\frac {d}{dz}}f_{c}(z_{0})=2z_{0}.

Σε ένα' περιοδικό σημείο z₀ περιόδου p η πρώτη παράγωγος μιας συνάρτησης

(f_{c}^{p})'(z_{0})={\frac {d}{dz}}f_{c}^{p}(z_{0})=\prod _{i=0}^{p-1}f_{c}'(z_{i})=2^{p}\prod _{i=0}^{p-1}z_{i}=\lambda

συχνά παριστάνεται με $\lambda$ και αναφέρεται ως πολλαπλασιαστής ή χαρακτηριστικός αριθμός Lyapunov. Ο λογάριθμός του είναι γνωστός ως εκθέτης Λιαπουνόφ. Η απόλυτη τιμή του πολλαπλασιαστή χρησιμοποιείται για τον έλεγχο της σταθερότητας των περιοδικών (επίσης σταθερών) σημείων.

Σε ένα μη περιοδικό σημείο, η παράγωγος, που συμβολίζεται με $z'_{n}$ , μπορεί να βρεθεί με επανάληψη ξεκινώντας με

z'_{0}=1,

και στη συνέχεια χρησιμοποιώντας

z'_{n}=2*z_{n-1}*z'_{n-1}.

Αυτή η παράγωγος χρησιμοποιείται για τον υπολογισμό της εξωτερικής απόστασης από το σύνολο Julia.

Παράγωγος Σβάρτζιαν[Επεξεργασία | επεξεργασία κώδικα]

Η παράγωγος Σβάρτζιαν (SD για συντομία) της f είναι:^[26]

(Sf)(z)={\frac {f'''(z)}{f'(z)}}-{\frac {3}{2}}\left({\frac {f''(z)}{f'(z)}}\right)^{2}.

Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]

Monica Nevins and Thomas D. Rogers, "Quadratic maps as dynamical systems on the p-adic numbers^{[νεκρός σύνδεσμος]}"
Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
More about Quadratic Maps : Quadratic Map

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]

↑ Poirier, Alfredo (1993). «On postcritically finite polynomials, part 1: Critical portraits». arXiv:math/9305207.
↑ ^2,0 ^2,1 «Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials» (PDF).
↑ Bodil Branner: Holomorphic dynamical systems in the complex plane. Mat-Report No 1996-42. Technical University of Denmark
↑ Dynamical Systems and Small Divisors, Editors: Stefano Marmi, Jean-Christophe Yoccoz, page 46
↑ «Show that the familiar logistic map $x_{n+1} = sx_n(1 - x_n)$, can be recoded into the form $x_{n+1} = x_n^2 + c$». Mathematics Stack Exchange.
↑ Yunping Jing : Local connectivity of the Mandelbrot set at certain infinitely renormalizable points Complex Dynamics and Related Topics, New Studies in Advanced Mathematics, 2004, The International Press, 236-264
↑ Weisstein, Eric W. «Quadratic Map». mathworld.wolfram.com.
↑ Java program by Dieter Röß showing result of changing initial point of Mandelbrot iterations Αρχειοθετήθηκε 26 April 2012 στο Wayback Machine.
↑ «Convex Julia sets». MathOverflow.
↑ Richards, Trevor (11 May 2015). «Conformal equivalence of analytic functions on compact sets». arXiv:1505.02671v1 [math.CV].
↑ M. Romera Αρχειοθετήθηκε 22 June 2008 στο Wayback Machine., G. Pastor Αρχειοθετήθηκε 1 May 2008 στο Wayback Machine., and F. Montoya : Multifurcations in nonhyperbolic fixed points of the Mandelbrot map. Αρχειοθετήθηκε 11 December 2009 στο Wayback Machine. Fractalia Αρχειοθετήθηκε 19 September 2008 στο Wayback Machine. 6, No. 21, 10-12 (1997)
↑ Burns A M : Plotting the Escape: An Animation of Parabolic Bifurcations in the Mandelbrot Set. Mathematics Magazine, Vol. 75, No. 2 (Apr., 2002), pp. 104–116
↑ «Khan Academy». Khan Academy.
↑ Ο δρόμος προς το χάος είναι γεμάτος με πολυωνυμικές καμπύλες των Richard D. Neidinger και R. John Annen III. American Mathematical Monthly, Vol. 103, No. 8, October 1996, pp. 640-653
↑ Hao, Bailin (1989). Elementary Symbolic Dynamics and Chaos in Dissipative Systems. World Scientific. ISBN 9971-5-0682-3. Αρχειοθετήθηκε από το πρωτότυπο στις 5 Δεκεμβρίου 2009. Ανακτήθηκε στις 2 Δεκεμβρίου 2009.
↑ «M. Romera, G. Pastor and F. Montoya, "Misiurewicz points in one-dimensional quadratic maps", Physica A, 232 (1996), 517-535. Preprint» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 2 Οκτωβρίου 2006.
↑ «Julia-Mandelbrot Space, Mu-Ency at MROB». www.mrob.com.
↑ Carleson, Lennart, Gamelin, Theodore W.: Complex Dynamics Series: Universitext, Subseries: Universitext: Tracts in Mathematics, 1st ed. 1993. Corr. 2nd printing, 1996, IX, 192 p. 28 illus., (ISBN 978-0-387-97942-7)
↑ Holomorphic motions and puzzels by P Roesch
↑ Rempe, Lasse; Schleicher, Dierk (12 May 2008). «Bifurcation Loci of Exponential Maps and Quadratic Polynomials: Local Connectivity, Triviality of Fibers, and Density of Hyperbolicity». arXiv:0805.1658 [math.DS].
↑ «Julia and Mandelbrot sets, alternate planes». aleph0.clarku.edu.
↑ «Exponential Map, Mu-Ency at MROB». mrob.com.
↑ Trees of visible components in the Mandelbrot set by Virpi K a u k o , FUNDAM E N TA MATHEMATICAE 164 (2000)
↑ «The Mandelbrot Set is named after mathematician Benoit B». www.sgtnd.narod.ru.
↑ Moehlis, Kresimir Josic, Eric T. Shea-Brown (2006) Periodic orbit. Scholarpedia,
↑ «Lecture Notes | Mathematical Exposition | Mathematics». MIT OpenCourseWare.

[1] Poirier, Alfredo (1993). «On postcritically finite polynomials, part 1: Critical portraits». arXiv:math/9305207.

[auto-2] 2,0 ^2,1 «Michael Yampolsky, Saeed Zakeri : Mating Siegel quadratic polynomials» (PDF).

[3] Bodil Branner: Holomorphic dynamical systems in the complex plane. Mat-Report No 1996-42. Technical University of Denmark

[4] Dynamical Systems and Small Divisors, Editors: Stefano Marmi, Jean-Christophe Yoccoz, page 46

[5] «Show that the familiar logistic map $x_{n+1} = sx_n(1 - x_n)$, can be recoded into the form $x_{n+1} = x_n^2 + c$». Mathematics Stack Exchange.

[6] Yunping Jing : Local connectivity of the Mandelbrot set at certain infinitely renormalizable points Complex Dynamics and Related Topics, New Studies in Advanced Mathematics, 2004, The International Press, 236-264

[7] Weisstein, Eric W. «Quadratic Map». mathworld.wolfram.com.

[8] Java program by Dieter Röß showing result of changing initial point of Mandelbrot iterations Αρχειοθετήθηκε 26 April 2012 στο Wayback Machine.

[9] «Convex Julia sets». MathOverflow.

[10] Richards, Trevor (11 May 2015). «Conformal equivalence of analytic functions on compact sets». arXiv:1505.02671v1 [math.CV].

[11] M. Romera Αρχειοθετήθηκε 22 June 2008 στο Wayback Machine., G. Pastor Αρχειοθετήθηκε 1 May 2008 στο Wayback Machine., and F. Montoya : Multifurcations in nonhyperbolic fixed points of the Mandelbrot map. Αρχειοθετήθηκε 11 December 2009 στο Wayback Machine. Fractalia Αρχειοθετήθηκε 19 September 2008 στο Wayback Machine. 6, No. 21, 10-12 (1997)

[12] Burns A M : Plotting the Escape: An Animation of Parabolic Bifurcations in the Mandelbrot Set. Mathematics Magazine, Vol. 75, No. 2 (Apr., 2002), pp. 104–116

[13] «Khan Academy». Khan Academy.

[14] Ο δρόμος προς το χάος είναι γεμάτος με πολυωνυμικές καμπύλες των Richard D. Neidinger και R. John Annen III. American Mathematical Monthly, Vol. 103, No. 8, October 1996, pp. 640-653

[15] Hao, Bailin (1989). Elementary Symbolic Dynamics and Chaos in Dissipative Systems. World Scientific. ISBN 9971-5-0682-3. Αρχειοθετήθηκε από το πρωτότυπο στις 5 Δεκεμβρίου 2009. Ανακτήθηκε στις 2 Δεκεμβρίου 2009.

[16] «M. Romera, G. Pastor and F. Montoya, "Misiurewicz points in one-dimensional quadratic maps", Physica A, 232 (1996), 517-535. Preprint» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 2 Οκτωβρίου 2006.

[17] «Julia-Mandelbrot Space, Mu-Ency at MROB». www.mrob.com.

[18] Carleson, Lennart, Gamelin, Theodore W.: Complex Dynamics Series: Universitext, Subseries: Universitext: Tracts in Mathematics, 1st ed. 1993. Corr. 2nd printing, 1996, IX, 192 p. 28 illus., (ISBN 978-0-387-97942-7)

[19] Holomorphic motions and puzzels by P Roesch

[20] Rempe, Lasse; Schleicher, Dierk (12 May 2008). «Bifurcation Loci of Exponential Maps and Quadratic Polynomials: Local Connectivity, Triviality of Fibers, and Density of Hyperbolicity». arXiv:0805.1658 [math.DS].

[21] «Julia and Mandelbrot sets, alternate planes». aleph0.clarku.edu.

[22] «Exponential Map, Mu-Ency at MROB». mrob.com.

[23] Trees of visible components in the Mandelbrot set by Virpi K a u k o , FUNDAM E N TA MATHEMATICAE 164 (2000)

[24] «The Mandelbrot Set is named after mathematician Benoit B». www.sgtnd.narod.ru.

[25] Moehlis, Kresimir Josic, Eric T. Shea-Brown (2006) Periodic orbit. Scholarpedia,

[26] «Lecture Notes | Mathematical Exposition | Mathematics». MIT OpenCourseWare.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]