Πίνακας DFT

Στα εφαρμοσμένα μαθηματικά, ένας πίνακας DFT είναι η έκφραση ενός διακριτού μετασχηματισμού Φουριέ (DFT) ως πίνακα μετασχηματισμού, ο οποίος μπορεί να εφαρμοστεί σε ένα σήμα μέσω πολλαπλασιασμού πινάκων.

Ορισμός

Ένας Ν-σημείο DFT εκφράζεται ως ο πολλαπλασιασμός $X=Wx$, όπου $x$ είναι το αρχικό σήμα εισόδου, $W$ είναι το Ν-προς-Ν τετράγωνο πίνακας DFT, και $X$ είναι ο DFT του σήματος.

Ο πίνακας μετασχηματισμού $W$ μπορεί να οριστεί ως $W=\left({\frac {\omega ^{jk}}{\sqrt {N}}}\right)_{j,k=0,\ldots ,N-1}$, or equivalently:

$W={\frac {1}{\sqrt {N}}}{\begin{bmatrix}1&1&1&1&\cdots &1\\1&\omega &\omega ^{2}&\omega ^{3}&\cdots &\omega ^{N-1}\\1&\omega ^{2}&\omega ^{4}&\omega ^{6}&\cdots &\omega ^{2(N-1)}\\1&\omega ^{3}&\omega ^{6}&\omega ^{9}&\cdots &\omega ^{3(N-1)}\\\vdots &\vdots &\vdots &\vdots &\ddots &\vdots \\1&\omega ^{N-1}&\omega ^{2(N-1)}&\omega ^{3(N-1)}&\cdots &\omega ^{(N-1)(N-1)}\end{bmatrix}}$,

όπου $\omega =e^{-2\pi i/N}$ είναι μια πρωταρχική Ν-η ρίζα της μονάδας στην οποία $i^{2}=-1$. Έτσι, μπορούμε να αποφύγουμε να γράψουμε μεγάλους εκθέτες για το $\omega$ χρησιμοποιώντας το γεγονός ότι για κάθε εκθέτη $x$ έχουμε την ταυτότητα $\omega ^{x}=\omega ^{x{\bmod {N}}}.$ Αυτός είναι ο πίνακας Βαντερμόντ για τις ρίζες της ενότητας, μέχρι τον παράγοντα κανονικοποίησης. Σημειώστε ότι ο παράγοντας κανονικοποίησης μπροστά από το άθροισμα ( $1/{\sqrt {N}}$ ) και το πρόσημο του εκθέτη στο ω είναι απλώς συμβάσεις και διαφέρουν σε ορισμένες επεξεργασίες. Όλη η συζήτηση που ακολουθεί ισχύει ανεξάρτητα από τη σύμβαση, το πολύ με μικρές προσαρμογές. Το μόνο σημαντικό είναι ότι ο εμπρόσθιος και ο αντίστροφος μετασχηματισμός έχουν εκθέτες με αντίθετο πρόσημο και ότι το γινόμενο των παραγόντων κανονικοποίησής τους είναι 1/N. Ωστόσο, η επιλογή $1/{\sqrt {N}}$ εδώ καθιστά τον προκύπτοντα πίνακα DFT μοναδιαίος, κάτι που είναι βολικό σε πολλές περιπτώσεις.

Οι αλγόριθμοι γρήγορου μετασχηματισμού Φουριέ χρησιμοποιούν τις συμμετρίες του πίνακα για να μειώσουν το χρόνο πολλαπλασιασμού ενός διανύσματος με τον πίνακα αυτό, από το συνηθισμένο $O(N^{2})$. Παρόμοιες τεχνικές μπορούν να εφαρμοστούν για πολλαπλασιασμούς με πίνακες όπως ο πίνακας Ανταμάρ και ο Πίνακας Γουάλς.

Παράδειγμα

Δύο σημεία

Ο DFT δύο σημείων είναι μια απλή περίπτωση, στην οποία η πρώτη εγγραφή είναι το DC (άθροισμα) και η δεύτερη εγγραφή είναι το AC (διαφορά).

$W={\frac {1}{\sqrt {2}}}{\begin{bmatrix}1&1\\1&-1\end{bmatrix}}$

Η πρώτη σειρά εκτελεί το άθροισμα και η δεύτερη σειρά εκτελεί τη διαφορά.

Ο παράγοντας $1/{\sqrt {2}}$ είναι για να γίνει ο μετασχηματισμός μοναδιαίος (βλ. παρακάτω).

Τέσσερα σημεία

Ο δεξιόστροφος πίνακας DFT τεσσάρων σημείων έχει ως εξής:

$W={\frac {1}{\sqrt {4}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\omega ^{3}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\omega ^{6}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\omega ^{9}\\\end{bmatrix}}={\frac {1}{\sqrt {4}}}{\begin{bmatrix}1&1&1&1\\1&-i&-1&i\\1&-1&1&-1\\1&i&-1&-i\end{bmatrix}}$

όπου $\omega =e^{-{\frac {2\pi i}{4}}}=-i$.

Οκτώ σημεία

Η πρώτη μη τετριμμένη περίπτωση ακέραιης δύναμης του δύο είναι για οκτώ σημεία:

$W={\frac {1}{\sqrt {8}}}{\begin{bmatrix}\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}&\omega ^{0}\\\omega ^{0}&\omega ^{1}&\omega ^{2}&\omega ^{3}&\omega ^{4}&\omega ^{5}&\omega ^{6}&\omega ^{7}\\\omega ^{0}&\omega ^{2}&\omega ^{4}&\omega ^{6}&\omega ^{8}&\omega ^{10}&\omega ^{12}&\omega ^{14}\\\omega ^{0}&\omega ^{3}&\omega ^{6}&\omega ^{9}&\omega ^{12}&\omega ^{15}&\omega ^{18}&\omega ^{21}\\\omega ^{0}&\omega ^{4}&\omega ^{8}&\omega ^{12}&\omega ^{16}&\omega ^{20}&\omega ^{24}&\omega ^{28}\\\omega ^{0}&\omega ^{5}&\omega ^{10}&\omega ^{15}&\omega ^{20}&\omega ^{25}&\omega ^{30}&\omega ^{35}\\\omega ^{0}&\omega ^{6}&\omega ^{12}&\omega ^{18}&\omega ^{24}&\omega ^{30}&\omega ^{36}&\omega ^{42}\\\omega ^{0}&\omega ^{7}&\omega ^{14}&\omega ^{21}&\omega ^{28}&\omega ^{35}&\omega ^{42}&\omega ^{49}\\\end{bmatrix}}={\frac {1}{\sqrt {8}}}{\begin{bmatrix}1&1&1&1&1&1&1&1\\1&\omega &-i&-i\omega &-1&-\omega &i&i\omega \\1&-i&-1&i&1&-i&-1&i\\1&-i\omega &i&\omega &-1&i\omega &-i&-\omega \\1&-1&1&-1&1&-1&1&-1\\1&-\omega &-i&i\omega &-1&\omega &i&-i\omega \\1&i&-1&-i&1&i&-1&-i\\1&i\omega &i&-\omega &-1&-i\omega &-i&\omega \\\end{bmatrix}}$

όπου

$\omega =e^{-{\frac {2\pi i}{8}}}={\frac {1}{\sqrt {2}}}-{\frac {i}{\sqrt {2}}}$

(Να σημειωθεί ότι $\omega ^{8+n}=\omega ^{n}$.)

Αξιολογώντας για την τιμή του $\omega$, προκύπτει:

$W={\frac {1}{\sqrt {8}}}{\begin{bmatrix}1&1&1&1&1&1&1&1\\1&{\frac {1-i}{\sqrt {2}}}&-i&{\frac {-1-i}{\sqrt {2}}}&-1&{\frac {-1+i}{\sqrt {2}}}&i&{\frac {1+i}{\sqrt {2}}}\\1&-i&-1&i&1&-i&-1&i\\1&{\frac {-1-i}{\sqrt {2}}}&i&{\frac {1-i}{\sqrt {2}}}&-1&{\frac {1+i}{\sqrt {2}}}&-i&{\frac {-1+i}{\sqrt {2}}}\\1&-1&1&-1&1&-1&1&-1\\1&{\frac {-1+i}{\sqrt {2}}}&-i&{\frac {1+i}{\sqrt {2}}}&-1&{\frac {1-i}{\sqrt {2}}}&i&{\frac {-1-i}{\sqrt {2}}}\\1&i&-1&-i&1&i&-1&-i\\1&{\frac {1+i}{\sqrt {2}}}&i&{\frac {-1+i}{\sqrt {2}}}&-1&{\frac {-1-i}{\sqrt {2}}}&-i&{\frac {1-i}{\sqrt {2}}}\\\end{bmatrix}}$

Η ακόλουθη εικόνα απεικονίζει τον DFT ως πολλαπλασιασμό πίνακα, με τα στοιχεία του πίνακα να απεικονίζονται με δείγματα μιγαδικών εκθετικών:

Το πραγματικό μέρος (συνημιτονοειδή κύματα) συμβολίζεται με συνεχή γραμμή και το φανταστικό μέρος (ημιτονοειδές κύμα) με διακεκομμένη γραμμή.

Η επάνω γραμμή είναι όλες μονάδες (κλιμακωμένες με $1/{\sqrt {8}}$ για μοναδιαία), οπότε «μετράει» τη συνιστώσα DC στο σήμα εισόδου. Η επόμενη σειρά είναι οκτώ δείγματα του αρνητικού ενός κύκλου ενός μιγαδικού εκθετικού, δηλαδή ένα σήμα με κλασματική συχνότητα -1/8, οπότε «μετράει» πόση «δύναμη» υπάρχει στην κλασματική συχνότητα +1/8 στο σήμα. Θυμηθείτε ότι ένα προσαρμοσμένο φίλτρο συγκρίνει το σήμα με μια χρονικά αντιστρεπτή έκδοση αυτού που ψάχνουμε, οπότε όταν ψάχνουμε για fracfreq. 1/8 συγκρίνουμε με fracfreq. -1/8, γι' αυτό και αυτή η σειρά έχει αρνητική συχνότητα. Η επόμενη σειρά είναι αρνητικοί δύο κύκλοι ενός μιγαδικού εκθετικού, με δειγματοληψία σε οκτώ θέσεις, άρα έχει κλασματική συχνότητα -1/4, και έτσι «μετράει» τον βαθμό στον οποίο το σήμα έχει κλασματική συχνότητα +1/4.

Τα παρακάτω συνοψίζουν τον τρόπο λειτουργίας του DFT 8 σημείων, γραμμή προς γραμμή, σε όρους κλασματικής συχνότητας:

• Το 0 μετράει πόσο DC υπάρχει στο σήμα.
• -1/8 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +1/8
• -1/4 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +1/4
• -3/8 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +3/8
• -1/2 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +1/2
• -5/8 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +5/8
• -3/4 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +3/4
• -7/8 μετράει πόσο μέρος του σήματος έχει κλασματική συχνότητα +7/8

Ισοδύναμα, η τελευταία σειρά μπορεί να θεωρηθεί ότι έχει κλασματική συχνότητα +1/8 και έτσι μετράμε πόσο μέρος του σήματος έχει κλασματική συχνότητα -1/8. Κατά αυτόν τον τρόπο, μπορούμε να ισχυριστούμε ότι οι άνω γραμμές του πίνακα «μετρούν» το θετικό συχνοτικό περιεχόμενο του σήματος και οι κάτω γραμμές το αρνητικό συχνοτικό συστατικό του σήματος.

Μετασχηματισμός μονάδων

Ο DFT είναι (ή μπορεί να είναι, μέσω κατάλληλης επιλογής της κλιμάκωσης) ένας μοναδιαίος μετασχηματισμός, δηλαδή ένας μετασχηματισμός που διατηρεί την ενέργεια. Η κατάλληλη επιλογή της κλιμάκωσης για την επίτευξη της μοναδιαίας μετατροπής είναι $1/{\sqrt {N}}$, έτσι ώστε η ενέργεια στο φυσικό πεδίο να είναι η ίδια με την ενέργεια στο πεδίο Φουριέ, δηλαδή να ικανοποιείται το θεώρημα του Παρσεβάλ. (Άλλες, μη μοναδιαίες, κλιμακώσεις, χρησιμοποιούνται επίσης συνήθως για υπολογιστική ευκολία- π.χ., το θεώρημα της συνέλιξης παίρνει μια ελαφρώς απλούστερη μορφή με την κλιμάκωση που παρουσιάζεται στο άρθρο διακριτός μετασχηματισμός Φουριέ).

Άλλες ιδιότητες

Για άλλες ιδιότητες του πίνακα DFT, συμπεριλαμβανομένων των ιδιοτιμών του, τη σύνδεση με τις συνελίξεις, τις εφαρμογές κ.ο.κ., ανατρέξτε στο άρθρο διακριτός μετασχηματισμός Φουριέ.

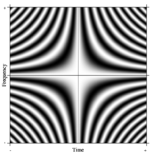
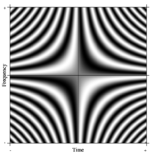
Μια περιοριστική περίπτωση: Ο τελεστής Φουριέ

Πραγματικό μέρος (συνημίτονο)

Φανταστικό μέρος (ημίτονο)

Ο τελεστής Φουριέ

Η έννοια του μετασχηματισμού Φουριέ γενικεύεται εύκολα. Μια τέτοια τυπική γενίκευση του DFT Ν-σημείων μπορεί να φανταστεί κανείς παίρνοντας το Ν αυθαίρετα μεγάλο. Στο όριο, ο αυστηρός μαθηματικός μηχανισμός αντιμετωπίζει τέτοιους γραμμικούς τελεστές ως λεγόμενους ολοκληρωτικούς μετασχηματισμούς. Σε αυτή την περίπτωση, αν φτιάξουμε έναν πολύ μεγάλο πίνακα με μιγαδικά εκθετικά στις γραμμές (δηλαδή συνημιτονικά πραγματικά μέρη και ημιτονικά φανταστικά μέρη) και αυξήσουμε την ανάλυση χωρίς όριο, πλησιάζουμε τον πυρήνα της ολοκληρωτικής εξίσωσης Φρέντχολμ του 2ου είδους, δηλαδή τον τελεστή Φουριέ που ορίζει τον συνεχή μετασχηματισμό Φουριέ. Ένα ορθογώνιο τμήμα αυτού του συνεχούς τελεστή Φουριέ μπορεί να απεικονιστεί ως εικόνα, ανάλογη με τον πίνακα DFT, όπως φαίνεται δεξιά, όπου η τιμή του εικονοστοιχείου σε κλίμακα του γκρι δηλώνει αριθμητική ποσότητα.

Δημοσιεύσεις

• Μαυρογιάννης, Ν. Σ. (Μαΐου 2016). «Μία εισαγωγή στους μιγαδικούς αριθμούς». Εκθέτης Φύλλα Μαθηματικής Παιδείας (16): 1-8. http://ekthetis.gr/Ekthetis016.pdf. 
• Bronshtein, I. N.· Semendyayev, K. A. (29 Ιουνίου 2013). Handbook of Mathematics. Springer Science & Business Media. ISBN 978-3-662-21982-9. 
• Belevitch V (1950). «Theory of 2n-terminal networks with applications to conference telephony». Electrical Communication 27: 231–244. 
• Goethals J.M., Seidel J.J. (1967). «Orthogonal matrices with zero diagonal». Canadian Journal of Mathematics 19: 1001–1010. doi:10.4153/cjm-1967-091-8. https://archive.org/details/sim_canadian-journal-of-mathematics_1967_19_5/page/1001. 
• Wilson, Robin (2018). Euler's Pioneering Equation: The Most Beautiful Theorem in Mathematics. Oxford: Oxford University Press. ISBN 978-0-19-879492-9. MR 3791469. 
• Brigham, E. Oran (1988). The fast Fourier transform and its applications. Englewood Cliffs, N.J.: Prentice Hall. ISBN 0-13-307505-2. 
• Oppenheim, Alan V.· Schafer, R. W.· Buck, J. R. (1999). Discrete-time signal processing. Upper Saddle River, N.J.: Prentice Hall. ISBN 0-13-754920-2. 
• Smith, Steven W. (1999). «Chapter 8: The Discrete Fourier Transform». The Scientist and Engineer's Guide to Digital Signal Processing (Second έκδοση). San Diego, Calif.: California Technical Publishing. ISBN 0-9660176-3-3. 

Δείτε επίσης

• Field Arithmetic
• Πραγματικό προβολικό επίπεδο
• Πραγματικός αριθμός
• Αντιερμιτιανός πίνακας
• Δέλτα του Κρόνεκερ
• Ταυτοτικός πίνακας
• Ελάσσων (γραμμική άλγεβρα)
• Προβολή (γραμμική άλγεβρα)
• Πεπερασμένο σώμα
• Αντιμεταθέσιμοι πίνακες
• Πολλαπλασιασμός πινάκων
• Μετασχηματισμός Φουριέ
• Διακριτός μετασχηματισμός Φουριέ
• High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

Εξωτερικοί σύνδεσμοι

• English - Greek Dictionary of Pure and Applied Mathematics Εθνικό Μετσόβιο Πολυτεχνείο
• Αγγλοελληνικό Λεξικό Μαθηματικής Ορολογίας - Πανεπιστήμιο Κύπρου
• Matrix calculator
• Matrix Analysis
• Complex-Valued Matrix Derivatives: With Applications in Signal Processing ...
• Mathematical Methods For Physicists
• Fourier Transforms: Approach to Scientific Principles
• Information Security and Privacy: 13th Australasian Conference, ACISP 2008 ...
• Physics and Combinatorics 2000: Proceedings of the Nagoya 2000 International ...
• Representation of Rings Over Skew Fields
• Multimedia Content Representation, Classification and Security ...
• Generalized Sylvester Equations: Unified Parametric Solutions

Παραπομπές

• Paley, R.E.A.C. (1933). «On orthogonal matrices». Journal of Mathematics and Physics 12: 311–320. doi:10.1002/sapm1933121311. . 
• Magdy Tawfik Hanna; Nabila Philip Attalla Seif; Waleed Abd El Maguid Ahmed (2004). «Hermite-Gaussian-like eigenvectors of the discrete Fourier transform matrix based on the singular-value decomposition of its orthogonal projection matrices». IEEE Trans. Circ. Syst. I 51 (11): 2245–2254. doi:10.1109/TCSI.2004.836850. 
• Shamgar Gurevich; Ronny Hadani (2009). «On the diagonalization of the discrete Fourier transform». Applied and Computational Harmonic Analysis 27 (1): 87–99. doi:10.1016/j.acha.2008.11.003. preprint at.