Μέγιστη πιθανοφάνεια

Στη στατιστική, η εκτίμηση μέγιστης πιθανοφάνειας (ΕΜΠ) είναι μια μέθοδος για την εκτίμηση των παραμέτρων από ένα στατιστικό μοντέλο δεδομένων.

Η μέθοδος της μέγιστης πιθανοφάνειας αντιστοιχεί σε πολλές γνωστές μεθόδους εκτίμησης της στατιστικής. Για παράδειγμα, μία από αυτές μπορεί να ενδιαφέρεται για τα ύψη των ενήλικων θηλυκών πιγκουίνων, αλλά δεν είναι σε θέση να μετρήσει το ύψος του κάθε πιγκουίνου σε ένα πληθυσμό λόγω των περιορισμών του κόστους ή του χρόνου. Αν υποτεθεί ότι τα ύψη ανήκουν στην Κανονική κατανομή με κάποιο άγνωστο, μέση τιμή και Διακύμανση, η μέση τιμή και η διακύμανση μπορούν να εκτιμηθούν με ΕΜΠ γνωρίζοντας μόνο τα ύψη από κάποιο δείγμα του συνολικού πληθυσμού. Η ΕΜΠ θα το πετύχει αυτό, λαμβάνοντας την μέση τιμή και η διακύμανση ως παραμέτρους και βρίσκοντας ειδικότερες παραμετρικές τιμές που κάνουν τα παρατηρούμενα αποτελέσματα πιο πιθανά δεδομένου του μοντέλου.

Σε γενικές γραμμές, για ένα σταθερό σύνολο των δεδομένων και των υποκείμενων στατιστικών μοντέλων, η μέθοδος της μέγιστης πιθανοφάνειας επιλέγει το σύνολο των τιμών των παραμέτρων του μοντέλου που μεγιστοποιεί την συνάρτηση πιθανότητας. Διαισθητικά, αυτό μεγιστοποιεί την "συμφωνία" από το επιλεγμένο μοντέλο με τα παρατηρούμενα δεδομένα, και για διακριτές τυχαίες μεταβλητές πραγματικά μεγιστοποιεί την πιθανότητα των παρατηρούμενων δεδομένων σύμφωνα με την τελική κατανομή. Η εκτίμηση μέγιστης πιθανοφάνειας δίνει μια ενιαία προσέγγιση για την εκτίμηση, η οποία είναι καλά ορισμένη στην περίπτωση της κανονικής κατανομής και πολλά άλλα προβλήματα.

Ιστορία

Ο Ρόναλντ Φίσερ στο 1913

Η εκτίμηση μέγιστης πιθανοφάνειας είχε προταθεί, αναλυθεί (με άκαρπες προσπάθειες αποδείξεις) και ευρέως διαδωθεί από τον Ρόναλντ Φίσερ μεταξύ 1912 και 1922 (αν και είχε χρησιμοποιηθεί νωρίτερα από τους Καρλ Φρίντριχ Γκάους, Πιερ Σιμόν Λαπλάς, Thorvald N Εσένα,Φράνσις Ισίντρο Έτζγουορθ). Περιλήψεις για την ανάπτυξη της μέγιστης πιθανοφάνειας έχουν παρασχεθεί από έναν αριθμό συγγραφέων.

Μερικά τμήματα από τη θεωρία εκτίμηση μέγιστης πιθανοφάνειας αναπτύχθηκαν για Στατιστική Baynes.

Αρχές

Ας υποθέσουμε ότι υπάρχει ένα δείγμα x₁, x₂, ..., x_n από n ανεξάρτητες και ταυτόσημα κατανεμημένες παρατηρήσεις, που προέρχονται από μια κατανομή με άγνωστη συνάρτηση πυκνότητας πιθανότητας f₀(·). Ωστόσο εικάζεται ότι η συνάρτηση f₀ ανήκει σε μια συγκεκριμένη οικογένεια κατανομών { f(·| θ), θ ∈ Θ } (όπου θ είναι φορέας των παραμέτρων για αυτή την οικογένεια), που ονομάζεται παραμετρικό μοντέλο, έτσι ώστε f₀ = f(·| θ₀). Η τιμή θ₀ είναι άγνωστη και αναφέρεται ως η πραγματική τιμή του φορέα της παραμέτρου. Είναι επιθυμητό να βρεθεί ένας εκτιμητής $\scriptstyle {\hat {\theta }}$ που θα είναι όσο πιο κοντά γίνεται στην πραγματική τιμή θ₀. Είτε μία από αυτές είτε και οι δύο οι παρατηρούμενες μεταβλητές x_i και η παράμετρος θ μπορεί να είναι φορείς.

Για να χρησιμοποιήσετε τη μέθοδο της μεγίστης πιθανοφάνειας, πρώτα καθορίζεται η από κοινού συνάρτηση πυκνότητας για όλες τις παρατηρήσεις. Για ένα ανεξάρτητο και ισόνομα κατανεμημένο δείγμα, αυτή η κοινή συνάρτηση πυκνότητας είναι

$f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )=f(x_{1}\mid \theta )\times f(x_{2}|\theta )\times \cdots \times f(x_{n}\mid \theta ).$

Τώρα κοιτάμε αυτή τη λειτουργία από μια διαφορετική προοπτική, λαμβάνοντας υπόψη τις παρατηρηθείσες τιμές x₁, x₂, ..., x_n να είναι σταθερές "παράμετροι" της λειτουργίας αυτής, όπου θ θα είναι η μεταβλητή της συνάρτησης και μπορεί να κυμαίνεται ελεύθερα· αυτή η λειτουργία θα ονομάζεται η πιθανοφάνεια:

${\mathcal {L}}(\theta \,;\,x_{1},\ldots ,x_{n})=f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )=\prod _{i=1}^{n}f(x_{i}\mid \theta ).$

Σημειώστε ότι το " $;$ " υποδηλώνει ένα διαχωρισμό μεταξύ των δύο ορισμάτων: $\theta$ και των παρατηρήσεων $x_{1},\ldots ,x_{n}$.

Στην πράξη, είναι συχνά πιο βολικό να συνεργαστεί με το λογάριθμο της συνάρτησης της πιθανοφάνειας, που ονομάζεται λογαριθμική-πιθανοφάνεια:

$\ln {\mathcal {L}}(\theta \,;\,x_{1},\ldots ,x_{n})=\sum _{i=1}^{n}\ln f(x_{i}\mid \theta ),$

ή μέση λογαριθμική-πιθανοφάνεια:

${\hat {\ell }}={\frac {1}{n}}\ln {\mathcal {L}}.$

Το καπέλο πάνω από το ℓ δείχνει ότι είναι παρόμοιο με κάποιο εκτιμητή. Πράγματι,το $\scriptstyle {\hat {\ell }}$ αντιπροσωπεύει την αναμενόμενη λογαριθμική-πιθανοφάνεια σε μία μόνο παρατήρηση στο μοντέλο.

Η μέθοδος της μέγιστης πιθανοφάνειας θ₀ , εκτιμάται βρίσκοντας μια τιμή του θ που μεγιστοποιεί το ${\hat {\ell }}(\theta ;x)$. Αυτή η μέθοδος εκτίμησης ορίζει τον εκτιμητή μέγιστης πιθανοφάνειας (ΕΜΠ) του θ₀:

$\{{\hat {\theta }}_{\mathrm {mle} }\}\subseteq \{{\underset {\theta \in \Theta }{\operatorname {arg\,max} }}\ {\hat {\ell }}(\theta \,;\,x_{1},\ldots ,x_{n})\},$

αν υπάρχει η μέγιστη. Μια ΕΜΠ εκτίμηση είναι η ίδια, ανεξάρτητα από το αν θα μεγιστοποιήσει την πιθανοφάνεια ή την συνάρτηση της λογαριθμικής πιθανοφάνειας, μιας και ο λογάριθμος είναι μονοτονικά αυξανόμενη συνάρτηση.

Για πολλά μοντέλα, ο εκτιμητής της μέγιστης πιθανοφάνειας μπορεί να βρεθεί ως μια ρητή συνάρτηση με τα δεδομένα παρατηρήσεων x₁, ..., x_n. Για πολλά άλλα μοντέλα, ωστόσο, καμία κλειστή μορφή λύσης για τη μεγιστοποίηση του προβλήματος είναι γνωστή ή διαθέσιμη, και μια ΕΜΠ πρέπει να βρεθεί αριθμητικά χρησιμοποιώντας βελτιστοποίηση μεθόδων. Για κάποια προβλήματα, μπορεί να υπάρχουν πολλές εκτιμήσεις που μεγιστοποιούν την πιθανοφάνεια. Για άλλα προβλήματα, δεν υπάρχει καμία εκτίμηση μέγιστης πιθανοφάνειας  (με την έννοια ότι η συνάρτηση της λογαριθμικής πιθανοφάνειας αυξάνεται χωρίς την χρήση του supremum ).

Στην παραπάνω έκθεση , θεωρείται ότι τα δεδομένα είναι ανεξάρτητα και ισόνομα κατανεμημένα. Η μέθοδος μπορεί να εφαρμοστεί, ωστόσο, σε ένα ευρύτερο πλαίσιο, όσο είναι δυνατόν να γράψετε την από κοινού συνάρτηση πυκνότητας f(x₁, ..., x_n | θ), και οι παράμετροι θ έχουν πεπερασμένη διάσταση, η οποία δεν εξαρτάται από το μέγεθος του δείγματος n. Σε μια πιο απλή επέκταση, ένα επίδομα μπορεί να γίνει για τα δεδομένα ετερογένεια, ώστε η κοινή πυκνότητα να είναι ίση με f₁(x₁ | θ) · f₂(x₂|θ) · ··· · f_n(x_n | θ). Με άλλα λόγια, υποθέτουμε τώρα ότι κάθε παρατήρηση x_i προέρχεται από μια τυχαία μεταβλητή που έχει τη δική της συνάρτηση κατανομής f _i . Στην πιο περίπλοκη περίπτωση των μοντέλων χρονοσειρών , η υπόθεση της ανεξαρτησίας μπορεί επίσης να πέσει.

Ένας εκτιμητής μέγιστης πιθανοφάνειας συμπίπτει με τον πιο πιθανό εκτιμητή Bayes έχοντας δοθεί μια συνεχής διανομή των παραμέτρων. Πράγματι, η μέγιστη εκ των υστέρων εκτίμηση της παραμέτρου θ που μεγιστοποιεί την πιθανότητα της θ δοσμένα στοιχεία, που δίνονται από Bayes θεώρημα:

$P(\theta \mid x_{1},x_{2},\ldots ,x_{n})={\frac {f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )P(\theta )}{P(x_{1},x_{2},\ldots ,x_{n})}}$

οπού $P(\theta )$ είναι η προηγούμενη διανομή της παραμέτρου θ και $P(x_{1},x_{2},\ldots ,x_{n})$ είναι η πιθανότητα των δεδομένων κατά μέσο όρο πάνω από όλες τις παραμέτρους. Αφού ο παρονομαστής είναι ανεξάρτητο του θ, ο εκτιμητής Bayes προκύπτει από τη μεγιστοποίηση της$f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )P(\theta )$ όσον αφορά το θ. Αν υποθέσουμε ότι η προηγούμενη $P(\theta )$ είναι μια ομοιόμορφη κατανομή, ο εκτιμητής Bayes προκύπτει από τη μεγιστοποίηση της συνάρτησης πιθανότητας $f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )$. Έτσι, ο εκτιμητής Bayes συμπίπτει με τον εκτιμητή μέγιστης πιθανοφάνειας για μία προηγούμενη ομοιόμορφη διανομή $P(\theta )$.

Ιδιότητες

Ένας εκτιμητής μέγιστης πιθανοφάνειας είναι ένα extremum εκτιμητής (minimum ή maximum) που λαμβάνεται με την μεγιστοποίηση, ως συνάρτηση του θ, της αντικειμενικής συνάρτησης (c.f., η λειτουργία απώλειας)

${\hat {\ell }}(\theta \mid x)={\frac {1}{n}}\sum _{i=1}^{n}\ln f(x_{i}\mid \theta ),$

αυτό είναι το δείγμα ανάλογο της αναμενόμενης λογαριθμικής-πιθανοφάνειας $\ell (\theta )=\operatorname {E} [\,\ln f(x_{i}\mid \theta )\,]$, όπου αυτή η αναμενόμενη τιμή έχει ληφθεί ως προς την πραγματική πυκνότητα $f(\cdot \mid \theta _{0})$.

Οι εκτιμητές μέγιστης πιθανοφάνειας δεν έχουν βέλτιστες ιδιότητες για πεπερασμένα δείγματα, με την έννοια ότι (όταν αξιολογούνται σε πεπερασμένα δείγματα) άλλοι εκτιμητές μπορεί να έχουν μεγαλύτερη συγκέντρωση γύρω από την πραγματική παραμετρική τιμή. Ωστόσο, όπως και σε άλλες μεθόδους εκτίμησης, η εκτίμηση μέγιστης πιθανοφάνειας διαθέτει μια σειρά από ελκυστικές οριακές ιδιότητες: Καθώς το μέγεθος του δείγματος αυξάνεται στο άπειρο, οι ακολουθίες των εκτιμητών μέγιστης πιθανοφάνειας έχουν αυτές τις ιδιότητες:

• Συνέπεια: η ακολουθία των ΕΜΠ συγκλίνει κατά πιθανότητα στην εκτιμώμενη τιμή .
• Ασυμπτωτική κανονικότητα: καθώς το μέγεθος του δείγματος αυξάνεται, η κατανομή των ΕΜΠ τείνει στην Gaussian κατανομή με μέση $\theta$ και πίνακα συνδιακύμανσης ίσο με το αντίστροφο του πληροφοριακού πίνακα του Φίσερ.
• Αποδοτικότητα, δηλαδή, επιτυγχάνει το Cramér–Rao κάτω φράγμα , όταν το μέγεθος του δείγματος τείνει στο άπειρο. Αυτό σημαίνει ότι κανένας συνεπής εκτιμητής δεν έχει χαμηλότερο ασυμπτωτικό μέσο τετραγωνικό σφάλμα από τον ΕΜΠ (ή άλλων εκτιμητών για την επίτευξη αυτού του φράγματος).
• Δεύτερης-τάξης απόδοτικότητα μετά από διόρθωση για την μεροληψία.

Συνέπεια

Υπό τις συνθήκες που περιγράφονται παρακάτω, ο εκτιμητής μέγιστης πιθανοφάνειας είναι συνεπής. Η συνέπεια σημαίνει ότι έχοντας ένα αρκετά μεγάλο αριθμό παρατηρήσεων n, είναι δυνατόν να βρεθεί η τιμή του θ₀ με αυθαίρετη ακρίβεια. Σε μαθηματικούς όρους, αυτό σημαίνει ότι καθώς το n τείνει στο άπειρο ο εκτιμητής $\scriptstyle {\hat {\theta }}$ συγκλίνει κατά πιθανότητα στην πραγματική του τιμή:

${\hat {\theta }}_{\mathrm {mle} }\ {\xrightarrow {p}}\ \theta _{0}.$

Υπό ελαφρώς ισχυρότερες συνθήκες, ο εκτιμητής συγκλίνει σχεδόν βέβαια (ή ισχυρά):

${\hat {\theta }}_{\mathrm {mle} }\ {\xrightarrow {\text{a.s.}}}\ \theta _{0}.$

Σε πρακτικές εφαρμογές, τα δεδομένα δεν παράγονται ποτέ από την $f(\cdot \,;\theta _{0})$. Περισσότερο, η $f(\cdot \,;\theta _{0})$ είναι ένα μοντέλο, συχνά σε μια ιδεατή μορφή, της διαδικασίας που παράγει τα δεδομένα. Είναι μια κοινή αφοριστική θεώρηση στη στατική σύμφωνα με την οποία όλα τα μοντέλα είναι εσφαλμένα. Έτσι, η πραγματική συνέπεια δεν επιτυγχάνεται στις πρακτικές εφαρμογές. Εντούτοις, η συνέπεια θεωρείται συχνά μια επιθυμητή ιδιότητα για έναν εκτιμητή.

Για να επιτευχθεί συνέπεια, οι ακόλουθες συνθήκες είναι επαρκείς:

1. Αναγνωρισιμότητα του μοντέλου:

   $\theta \neq \theta _{0}\quad \Leftrightarrow \quad f(\cdot \mid \theta )\neq f(\cdot \mid \theta _{0}).$

   Με άλλα λογια, διαφορετικές τιμές της παραμέτρου θ αντιστοιχούν σε διαφορετικές κατανομές στα πλαίσια του μοντέλου. Εάν αυτή η συνθήκη δεν ίσχυε, θα υπήρχε μια τιμή θ₁ τέτοια ώστε η θ₀ και η θ₁ θα παρήγαγαν την ίδια κατανομή από τα παρατηρήσιμα δεδομένα. Τότε, δεν θα ήμαστε σε θέση να ξεχωρίσουμε αυτές τις δυο παραμέτρους ακόμα και με άπειρο πλήθος δεδομένων- αυτές οι παράμετροι θα ήταν "ισοδύναμες" ως προς τις παρατηρήσεις (observationally equivalent.)
   

   Η συνθήκη αναγνώρισιμότητας είναι απολύτως απαραίτητη για να είναι ένας ΕΜΠ συνεπής. Όταν ισχύει αυτή η συνθήκη, τότε η οριακή συνάρτηση πιθανοφάνειας ℓ(θ|·) έχει μοναδικό ολικό μέγιστο στο θ₀.
2. Συμπάγεια:ο παραμετρικός χώρος Θ του μοντέλου είναι συμπαγής.

   

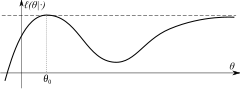
   Η συνθήκη αναγνώρισης θεμελιώνει ότι ο λογάριθμος της πιθανοφάνειας έχει μοναδικό ολικό μέγιστο. Η συμπάγεια συνεπάγεται ότι η πιθανοφάνεια δεν μπορεί να προσεγγίσει τη μέγιστη τιμή αυθαίρετα κοντά σε ένα άλλο σημείο (όπως φαίνεται στο παράδειγμα της εικόνας στα δεξιά.

   Η συμπάγεια είναι μόνο επαρκής συνθήκη και όχι αναγκαία. Η συμπάγεια δύναται να αντικατασταθεί από άλλες συνθήκες, όπως:

   • τόσο η κυρτότητα της συνάρτησης του λογαρίθμου της συνάρτησης πιθανοφάνειας και η συμπάγεια ενός (nonempty) upper level sets του λογαρίθμου της συνάρτησης πιθανοφάνειας, ή
   • η ύπαρξη μιας συμπαγούς γειτονιάς N του θ₀ τέτοια ώστε έξω από το N η συνάρτηση του λογαρίθμου της συνάρτησης πιθανοφάνειας είναι μικρότερη από το μέγιστο κατά τουλάχιστον κάποιο ε > 0.
3. Συνέχεια: η συνάρτηση ln f(x | θ) είναι συνεχής στο is θ για όλες σχεδόν τις τιμές του x:

   $\operatorname {\mathbb {P} } {\Bigl [}\;\ln f(x\mid \theta )\;\in \;C^{0}(\Theta )\;{\Bigr ]}=1.$

   Η συνέχεια εδώ μπορεί να αντικατασταθεί από μια ελαφρώς ασθενέστερη συνθήκη της "άνω ημισυνέχειας" upper semi-continuity.
4. Κυριαρχία (Dominance): υπάρχει D(x) ολοκληρώσιμη ως προς την κατανομή f(x | θ₀) έτσι ώστε

   ${\Bigl |}\ln f(x\mid \theta ){\Bigr |}<D(x)\quad {\text{ for all }}\theta \in \Theta .$

   By the uniform law of large numbers, η συνθήκη κυριαρχίας μαζί με τη συνέχεια θεμελιώνουν μια ομοιόμορφη σύγκλιση κατά πιθανότητα του λογαρίθμου της πιθανοφάνειας:

   $\sup _{\theta \in \Theta }\left|{\hat {\ell \,}}(\theta \mid x)-\ell (\theta )\,\right|\ \xrightarrow {\text{p}} \ 0.$

Η συνθήκη της κυριαρχίας μπορεί να χρησιμοποιηθεί στην περίπτωση των Ανεξάρτητων και ισόνομων παρατηρήσεων. Στην περίπτωση των μη-ισόνομων και ανεξάρτητων τυχαίων μεταβλητών, η ομοιόμορφη σύγκλιση κατά πιθανότητα μπορεί να ελεγχθεί δείχνοντας ότι η ακολουθία $\scriptstyle {\hat {\ell }}(\theta \mid x)$ είναι is στοχαστικά equicontinuous. Αν κάποιος θέλει να αποδείξει ότι ο ΕΜΠ $\scriptstyle {\hat {\theta }}$ συγκλίνει στο θ₀ σχεδόν βέβαια, τότε μια ισχυρότερη συνθήκη της ομοιόμορφης σχεδόν βέβαιης σύγκλισης πρέπει να επιβληθεί:

$\sup _{\theta \in \Theta }{\big \|}\;{\hat {\ell }}(x\mid \theta )-\ell (\theta )\;{\big \|}\ {\xrightarrow {\text{a.s.}}}\ 0.$

Επιπροσθέτως, εαν (όπως έχει υποτεθεί ανωτέρω) τα δεδομένα παραγόντουσαν από την $f(\cdot \,;\theta _{0})$, τότε κάτω από ορισμένες συνθήκες μπορεί να δειχθεί ότι ο ΕΜΠ συγκλίνει κατά νόμο στην κανονική κατανομή. Ειδικότερα,

${\sqrt {n}}\left({\widehat {\theta \,}}_{\mathrm {mle} }-\theta _{0}\right)\ \xrightarrow {d} \ {\mathcal {N}}\left(0,\,I^{-1}\right)$

όπου I είναι ο πίνακας πληροφορίας του Fisher.

Συναρτησιακή ισομεταβλητότητα (Functional equivariance)

Ο EMP επιλέγει την τιμή της παραμέτρου η οποία δίνει τα παρατηρούμενα δεδομένα όσο το δυνατόν μεγαλύτερη πιθανότητα (ή πυκνότητα πιθανότητας, στη συνεχή περίπτωση). Αν η παράμετρος αποτελείται από έναν αριθμό στοιχείων, τότε ορίζουμε τους ξεχωριστούς εκτιμητές μέγιστης πιθανοφάνειας, όπως και την αντίστοιχη συνιστώσα του ΕΜΠ της πλήρους παραμέτρου. Σύμφωνα με αυτό, αν ${\widehat {\theta }}$ είναι ο ΕΜΠ για το θ, και αν g(θ) είναι οποιοσδήποτε μετασχηματισμός της θ, τότε ο ΕΜΠ για α = g(θ) είναι εξ ορισμού

${\widehat {\alpha }}=g(\,{\widehat {\theta }}\,).\,$

Μεγιστοποιεί το λεγόμενο προφίλ πιθανότητας (profile likelihood):

${\bar {L}}(\alpha )=\sup _{\theta :\alpha =g(\theta )}L(\theta ).\,$

Οι ΕΜΠ είναι επίσης ισομεταβλητές (equivariant) σε σχέση με ορισμένους μετασχηματισμούς των δεδομένων. Αν Y = g(X), όπου g είναι ένα προς ένα και δεν εξαρτάται από τις παραμέτρους που θα πρέπει να εκτιμηθούν, τότε οι συναρτήσεις πυκνότητας ικανοποιούν την :

$f_{Y}(y)={\frac {f_{X}(x)}{|g'(x)|}}$

και ως εκ τούτου οι συναρτήσεις πιθανοφάνειας για τις X και Y διαφέρουν μόνο κατά ένα συντελεστή που δεν εξαρτάται από τις παραμέτρους του μοντέλου.

Για παράδειγμα, οι ΕΜΠ-παράμετροι της λογαριθμικής-κανονικής κατανομής είναι οι ίδιες με αυτές της κανονικής κατανομής που προσαρμόζεται τον λογάριθμο των δεδομένων.

Αποδοτικότητα

Όπως υποτίθεται παραπάνω, εάν τα δεδομένα παραγόντουσαν από την https://wikimedia.org/api/rest_v1/media/math/render/svg/e8c6dbb6ff21ff22012fca066c1115ef63f4a590 τότε υπό ορισμένες προϋποθέσεις, μπορεί ακόμη να δειχθεί ότι ο ΕΜΠ συγκλίνει κατά νόμο στην κανονική κατανομή. Είναι √n-συνεπής και ασυμπτωτικά αποδοτικός, πράγμα που σημαίνει ότι πλησιάζει το όριο Cramér–Rao. Συγκεκριμένα:

${\sqrt {n}}({\hat {\theta }}_{\text{mle}}-\theta _{0})\ \ {\xrightarrow {d}}\ \ {\mathcal {N}}(0,\ I^{-1}),$

όπού I  είναι ο πίνακας πληροφορίας του Fisher :

$I_{jk}=\operatorname {E} _{X}{\bigg [}\;{-{\frac {\partial ^{2}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{j}\,\partial \theta _{k}}}}\;{\bigg ]}.$

Ειδικότερα, αυτό σημαίνει ότι η μεροληψία του ΕΜΠ είναι ίση με το μηδέν μέχρι και την τάξη n^-1/2.

Δεύτερης-τάξης αποδοτικότητα έπειτα από τη διόρθωση της μεροληψίας

Ωστόσο, όταν εξετάζουμε υψηλής-τάξης όρους στην επέκταση της κατανοής του εκτιμητή, προκύπτει ότι ο θ_mle έχει μεροληψία τάξης n^-1. Αυτή η μεροληψία ισούται (κατά συνιστώσα) με:

$b_{s}\equiv \operatorname {E} [({\hat {\theta }}_{\mathrm {mle} }-\theta _{0})_{s}]={\frac {1}{n}}\cdot I^{si}I^{jk}{\big (}{\tfrac {1}{2}}K_{ijk}+J_{j,ik}{\big )}$

όπου το ${\mathcal {I}}^{jk}$https://wikimedia.org/api/rest_v1/media/math/render/svg/95ea54922b0b2f15bb16fc33b9545388081c71f7(με άνω δείκτες) δηλώνει την (j,k)-στή συνιστώσα του αντιστρόφου πίνακας πληροφορίας του Fisher, και

${\tfrac {1}{2}}K_{ijk}+J_{j,ik}=\operatorname {E} _{X}{\bigg [}\;{\frac {1}{2}}{\frac {\partial ^{3}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{i}\,\partial \theta _{j}\,\partial \theta _{k}}}+{\frac {\partial \ln f_{\theta _{0}}(X_{t})}{\partial \theta _{j}}}{\frac {\partial ^{2}\ln f_{\theta _{0}}(X_{t})}{\partial \theta _{i}\,\partial \theta _{k}}}\;{\bigg ]}.$

Χρησιμοποιώντας αυτούς τους τύπους είναι δυνατόν να εκτιμηθεί η δεύτερης τάξης μεροληψία του ΕΜΠ, και να επιτευχθεί διόρθωση με την αφαίρεση:

${\hat {\theta }}_{\mathrm {mle} }^{*}={\hat {\theta }}_{\mathrm {mle} }-{\hat {b}}.$

Αυτός ο εκτιμητής είναι αμερόληπτος μέχρι τους όρους τάξης n^-1, και ονομάζεται ο bias-corrected (ελεύθερος-μεροληψίας;) ΕΜΠ.

Αυτός ο bias-corrected εκτιμητής είναι δεύτερης τάξης αποδοτικός (τουλάχιστον στα πλαίσια της κυρτής εκθετικής οικογένειας), με την έννοια ότι έχει ελάχιστο μέσο τετραγωνικό σφάλμα μεταξύ όλων των δεύτερης τάξης bias-corrected εκτιμητών, μέχρι τους όρους της σειράς n^-2. Είναι δυνατόν να συνεχιστεί αυτή η διαδικασία, δηλαδή η εξαγωγή τρίτης τάξης όρων διόρθωσης της μεροληψίας, και ούτω καθεξής. Ωστόσο, όπως φαίνεται από τον Kano (1996), ο εκτιμητής μέγιστης πιθανοφάνειας δεν είναι τρίτης τάξης αποδοτικός.

Σχέση με τη συμπερασματολογία κατά Bayes

Ένας ΕΜΠ συμπίπτει με το πιο πιθανό εκτιμητή Bayes δοθείσης ομοιόμορφης εκ των προτέρων κατανομής για τις παραμέτρους. Πράγματι, ο maximum a posteriori estimate είναι η παράμετρος θ που μεγιστοποιεί την πιθανότητα του θ δεσμευμένη στα δεδομένα, βάσει του θεωρήματος Bayes:

$\operatorname {\mathbb {P} } (\theta \mid x_{1},x_{2},\ldots ,x_{n})={\frac {f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )\operatorname {\mathbb {P} } (\theta )}{\operatorname {\mathbb {P} } (x_{1},x_{2},\ldots ,x_{n})}}$

όπου $\operatorname {\mathbb {P} } (\theta )$ είναι η εκ των προτέρων κατανοή για την παράμετρο θ και $\operatorname {\mathbb {P} } (x_{1},x_{2},\ldots ,x_{n})$ είναι η πιθανόητητα των δεδομένων κανονικοποιημένη για όλες τις παραμέτρους (averaged over all parameters). Αφού ο παρονομαστής εξαρτάται από το θ, ο εκτιμητής Bayes αποκτάται με τη μεγιστοποίησης της ποσότητας$f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )\operatorname {\mathbb {P} } (\theta )$ ως προς θ. Εάν υποθέσουμε περαιτέρω ότι η εκ των προτέρων κατανομη $\operatorname {\mathbb {P} } (\theta )$ είναι η ομοιόμορφη, ο εκτιμητής Bayes αποκτάται με τη μεγιστοποίηση της συνάρτησης πιθανοφάνειας $f(x_{1},x_{2},\ldots ,x_{n}\mid \theta )$. Έτσι, ο εκτιμητής Bayes συμπίπτει με τον ΕΜΠ για ομοιόμορφη εκ των προτέρων κατανομή $\operatorname {\mathbb {P} } (\theta )$.

Εφαρμογή της εκτίμησης μέγιστης πιθανοφάνειας στη θεωρία αποφάσεων Bayes

Σε πολλές πρακτικές εφαρμογές στη Μηχανική μάθηση (machine learning), η εκτίμηση μέγιστης πιθανοφάνειας αξιοποιείται για την εκτίμηση παραμέτρων του μοντέλου.

Η θεωρία αποφάσεων Bayes αφορά το σχεδιασμό μιας ταξινόμησης (classifier) που ελαχιστοποιεί τον αναμενόμενο κίνδυνο. Ειδικά, όταν τα κόστη (συνάρτηση απώλειας) που σχετίζονταιι με διαφορετικές αποφάσεις είναι ίσα, η ταξινόμηση είναι η ελαχιστοποίηση του σφάλματος για ολόκληρη την κατανομή.

Έτσι, ο κανόνας απόφασης Bayes διατυπώνεται ως

"αποφάσισε $\;w_{1}\;$ αν$~\operatorname {\mathbb {P} } (w_{1}|x)\;>\;\operatorname {\mathbb {P} } (w_{2}|x)~;~$ διαφορετικά αποφάσισε $\;w_{2}\;$"

όπου $\;w_{1}\,,w_{2}\;$ είναι προβλέψεις για διαφορετικές κλάσεις. Από μια προοπτική ελαχιστοποίησης σφαλμάτων, μπορεί ακόμη να εφραστεί ως

$w={\underset {w}{\operatorname {arg\;max} }}\;\int _{-\infty }^{\infty }\operatorname {\mathbb {P} } ({\text{ error}}\mid x)\operatorname {\mathbb {P} } (x)\,\operatorname {d} x~$

όπου

$\operatorname {\mathbb {P} } ({\text{ error}}\mid x)=\operatorname {\mathbb {P} } (w_{1}\mid x)~$

αν αποφασίσουμε $\;w_{2}\;$ και $\;\operatorname {\mathbb {P} } ({\text{ error}}\mid x)=\operatorname {\mathbb {P} } (w_{2}\mid x)\;$ αν αποφασίσουμε $\;w_{1}\;.$

Εφαρμόζοντας το Θεώρημα Bayes (Bayes' theorem)

$\operatorname {\mathbb {P} } (w_{i}\mid x)={\frac {\operatorname {\mathbb {P} } (x\mid w_{i})\operatorname {\mathbb {P} } (w_{i})}{\operatorname {\mathbb {P} } (x)}}$,

και εάν επιπλέον υποθέσουμε τη συνάρτηση απωλείας zero-or-one, η οποία είναι μια όμοια απώλεια για όλα τα σφάλματα, ο κανόνας απόφασης Bayes Decision δύναται να αναδιατυπωθεί ως

$h_{\text{Bayes}}={\underset {w}{\operatorname {arg\;max} }}\,{\bigl [}\,\operatorname {\mathbb {P} } (x\mid w)\,\operatorname {\mathbb {P} } (w)\,{\bigr ]}\;,$

όπου $h_{\text{Bayes}}$ είναι η πρόβλεψη και $\;\operatorname {\mathbb {P} } (w)\;$είναι η εκ των προτέρων πιθανότητα.

Σχέση με την ελαχιστοποίησης της απόκλεισης Kullback–Leibler και την cross εντροπία

Η εύρεση ΕΜΠ ${\hat {\theta }}$ είναι ασυμπτωτικά ισοδύναμη με την εύρεση του ${\hat {\theta }}$ που ορίζει την κατανομή πιθανότητας ($Q_{\hat {\theta }}$) που έχει την ελάχιστη απόσταση, στα πλαίσια της απόκλισης Kullback–Leibler (Kullback–Leibler divergence), στην πραγματική κατανομή από την οποία παράγονται τα δεδομένα μας (π.χ., παράγονται από την $P_{\theta _{0}}$). IΣε έναν ιδανικό κόσμο, P και Q είναι ίδιες (και το μόνο άγνωστο είναι το $\theta$ που καθορίζει την P). Ωστόσο, ακόμα και αν δεν είναι ίσες και το μοντέλο που χρησιμοποιούμε είναι εσφαλμένο, ακόμη οι ΕΜΠ θα μας δώσουν την "εγγύτερη" κατανομή (στα πλαίσια των περιορισμών ενός μοντέλου Q που εξαρτάται από το ${\hat {\theta }}$) στην πραγματική κατανομή $P_{\theta _{0}}$.

Απόδειξη. Για απλοποίηση των συμβολισμών, ας υποθέσουμε ότι P=Q. Έστω n i.i.d δείγματα δεδομένων $\mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})$ από κάποια πιθανότητα $y\sim P_{\theta _{0}}$, που εμείς προσπαθούμε να εκτιμήσουμε βρίσκοντας το ${\hat {\theta }}$ που θα μεγιστοποιήσει την πιθανοφάνεια με τη χρήση της $P_{\theta }$, τότε:

${\begin{aligned}{\hat {\theta }}&={\underset {\theta }{\operatorname {arg\,max} }}\,L_{P_{\theta }}(\mathbf {y} )={\underset {\theta }{\operatorname {arg\,max} }}\,P_{\theta }(\mathbf {y} )={\underset {\theta }{\operatorname {arg\,max} }}\,P(\mathbf {y} \mid \theta )\\&={\underset {\theta }{\operatorname {arg\,max} }}\,\prod _{i=1}^{n}P(y_{i}\mid \theta )={\underset {\theta }{\operatorname {arg\,max} }}\,\sum _{i=1}^{n}\log P(y_{i}\mid \theta )\\&={\underset {\theta }{\operatorname {arg\,max} }}\,\left(\sum _{i=1}^{n}\log P(y_{i}\mid \theta )-\sum _{i=1}^{n}\log P(y_{i}\mid \theta _{0})\right)={\underset {\theta }{\operatorname {arg\,max} }}\,\sum _{i=1}^{n}\left(\log P(y_{i}\mid \theta )-\log P(y_{i}\mid \theta _{0})\right)\\&={\underset {\theta }{\operatorname {arg\,max} }}\,\sum _{i=1}^{n}\log {\frac {P(y_{i}\mid \theta )}{P(y_{i}\mid \theta _{0})}}={\underset {\theta }{\operatorname {arg\,min} }}\,\sum _{i=1}^{n}\log {\frac {P(y_{i}\mid \theta _{0})}{P(y_{i}\mid \theta )}}={\underset {\theta }{\operatorname {arg\,min} }}\,{\frac {1}{n}}\sum _{i=1}^{n}\log {\frac {P(y_{i}\mid \theta _{0})}{P(y_{i}\mid \theta )}}\\&={\underset {\theta }{\operatorname {arg\,min} }}\,{\frac {1}{n}}\sum _{i=1}^{n}h_{\theta }(y_{i})\quad {\underset {n\to \infty }{\longrightarrow }}\quad {\underset {\theta }{\operatorname {arg\,min} }}\,E[h_{\theta }(y)]\\&={\underset {\theta }{\operatorname {arg\,min} }}\,\int P_{\theta _{0}}(y)h_{\theta }(y)dy={\underset {\theta }{\operatorname {arg\,min} }}\,\int P_{\theta _{0}}(y)\log {\frac {P(y\mid \theta _{0})}{P(y\mid \theta )}}dy\\&={\underset {\theta }{\operatorname {arg\,min} }}\,D_{\text{KL}}(P_{\theta _{0}}\parallel P_{\theta })\end{aligned}}$

όπου $h_{\theta }(x)=\log {\frac {P(x\mid \theta _{0})}{P(x\mid \theta )}}$. Η χρηση της h μας βοηθά να δούμε πως χρησιμοποιουμε το νόμο των μεγάλων αριθμών (law of large numbers) για να προχωρήσουμε από το μέσου της h(x) στην αναμενόμενη τιμή (expectancy ) του χρησιμοποιώντας τον law of the unconscious statistician. Οι πρώτες (αρκετές- several) μεταβάσεις έχουν να κάνουν με νόμους λογαρίθμων (laws of logarithm) και ότι η εύρεση του ${\hat {\theta }}$ που μεγιστοποιεί κάποια συνάρτηση θα είναι επίσης μια που μεγιστοποιεί κάποιο μονότονο μετασχηματισμό εκείνης της συνάρτησης (iπ.χ. προσθέτοντας/πολλάπλασιάζοντας κατά σταθερά).

Αφού η cross entropy είναι απλά μια Shannon's Entropy συν μια απόκλιση KL και αφού η εντροπία της $P_{\theta _{0}}$είναι σταθερή, τότε ο ΕΜΠ ελαχιστοποιεί επίσης την cross entropy ασυμπτωτικά.

Ασυμπτωτική κανονικότητα

Σε ένα ευρύ φάσμα καταστάσεων, η παράμετρος του εκτιμητή της μέγιστης πιθανοφάνειας παρουσιάζει ασυμπτωτική κανονικότητα, δηλαδή είναι ίση με την πραγματική παράμετρο συν ένα τυχαίο σφάλμα, το οποίο είναι περίπου κανονικό (δίνονται επαρκή στοιχεία), και η απόκλιση του σφάλματος διασπάται ως 1/n. Για αυτό το ακίνητο σε αναμονή, είναι απαραίτητο ότι ο εκτιμητής δεν υποφέρει από τα ακόλουθα ζητήματα:

Εκτίμηση όριο

Μερικές φορές ο εκτιμητής μέγιστης πιθανοφάνειας βρίσκεται στο όριο από το σύνολο των πιθανών παραμέτρων, ή (αν το όριο δεν , για να κυριολεκτήσουμε, επιτρέπεται) η πιθανότητα γίνεται όλο και μεγαλύτερο καθώς η παράμετρος πλησιάζει το όριο. Η κλασσική ασυμπτωτική θεωρία χρειάζεται την υπόθεση ότι η πραγματική τιμή της παραμέτρου βρίσκεται μακριά από το όριο. Αν έχουμε αρκετά δεδομένα, ο εκτιμητής μέγιστης πιθανοφάνειας θα αποκλίνει από το όριο. Αλλά με μικρότερα δείγματα, η εκτίμηση μπορεί να βρίσκετε στο όριο. Σε τέτοιες περιπτώσεις, η ασυμπτωτική θεωρία σαφώς δεν δίνει μια πρακτικά χρήσιμη προσέγγιση. Παραδείγματα εδώ θα είναι διακύμανση-συστατικά μοντέλα, όπου κάθε συστατικό της διακύμανσης, σ², πρέπει να πληροί τον περιορισμό σ² ≥ 0.

Τα δεδομένα όρια παράμετρος-εξάρτηση 

Για να εφαρμοστεί η θεωρία με απλό τρόπο, το σύνολο των δεδομένων αξιών, το οποίο έχει θετική πιθανότητα (ή θετική πιθανότητα πυκνότητας) δεν θα πρέπει να εξαρτάται από την άγνωστη παράμετρος. Ένα απλό παράδειγμα όπου μια τέτοια παράμετρος-εξάρτηση δεν κατέχει είναι η περίπτωση, από την εκτίμηση του θ από ένα σύνολο από ανεξάρτητες και ισόνομα κατανεμημένες όταν η κοινή κατανομή είναι ομοιόμορφη για το εύρος (0,θ). Για εκτιμητικούς σκοπούς, η σχετική σειρά της θ είναι τέτοια που θ δεν μπορεί να είναι μικρότερη από τη μεγαλύτερη παρατήρηση. Επειδή το διάστημα (0,θ) δεν είναι συμπαγές, υπάρχει ανώτατο όριο για την συνάρτηση πιθανοφάνειας: Για κάθε εκτίμηση του θήτα, υπάρχει μια μεγαλύτερη εκτίμηση ότι, επίσης, έχει μεγαλύτερη πιθανότητα. Σε αντίθεση, το διάστημα [0,θ], περιλαμβάνει το τελικό σημείο θ και είναι συμπαγής, στην οποία περίπτωση ο εκτιμητής μέγιστης πιθανοφάνειας υπάρχει. Ωστόσο, στην περίπτωση αυτή, ο εκτιμητής μέγιστης πιθανοφάνειας είναι προκατειλημμένος. Ασυμπτωτικά, αυτός ο εκτιμητής μέγιστης πιθανοφάνειας δεν είναι κανονικά κατανεμημένος.

Ενόχληση παράμετρών

Για τον εκτιμητή μέγιστης πιθανοφάνειας, ένα μοντέλο μπορεί να έχει μια σειρά από ενόχληση παραμέτρους. Για την ασυμπτωτική συμπεριφορά που περιγράφεται σε αναμονή, ο αριθμός των ενοχλητικών παραμέτρων δεν θα πρέπει να αυξηθεί με τον αριθμό των παρατηρήσεων (το μέγεθος του δείγματος). Ένα πολύ γνωστό παράδειγμα αυτής της περίπτωσης είναι εκεί όπου οι παρατηρήσεις εμφανίζονται ως ζεύγη, όπου οι παρατηρήσεις σε κάθε ζευγάρι έχουν διαφορετικά (άγνωστα) μέσα, αλλά κατά τα άλλα οι παρατηρήσεις είναι ανεξάρτητες και κανονικά κατανεμημένες με κοινή διακύμανση. Εδώ για 2N παρατηρήσεις, υπάρχουν N + 1 παράμετροι. Είναι γνωστό ότι οι εκτιμητές μέγιστης πιθανοφάνειας της διακύμανσης δεν συγκλίνουν προς την πραγματική τιμή της διακύμανσης.

Περισσότερες πληροφορίες

Για τις ασύμπτωτες που κατέχουν σε περιπτώσεις όπου η υπόθεση των ανεξάρτητων και ισόνομα κατανεμημένων παρατηρήσεων δεν κατέχετε, βασική προϋπόθεση είναι ότι η ποσότητα των πληροφοριών των δεδομένων αυξάνει επ ' αόριστον, καθώς το μέγεθος του δείγματος αυξάνει. Μια τέτοια απαίτηση δεν μπορεί να ικανοποιηθεί αν, είτε υπάρχει υπερβολική εξάρτηση των δεδομένων (για παράδειγμα, εάν οι νέες παρατηρήσεις είναι πανομοιότυπες με τις υπάρχουσες παρατηρήσεις), ή εάν οι νέες ανεξάρτητες παρατηρήσεις υπόκεινται σε αύξηση των σφαλμάτων της παρατήρησης.

Κάποιες συνθήκες κανονικότητας που να διασφαλίζουν αυτή η συμπεριφορά είναι:

1. Η πρώτη και η δεύτερη παράγωγος της συνάρτησης της λογαριθμικής πιθανοφάνειας πρέπει να οριστεί.
2. Ο πίνακας πληροφοριών του Φίσερ  δεν πρέπει να είναι μηδέν, και πρέπει να είναι συνεχής, ως παραμετρική συνάρτηση.
3. Ο εκτιμητής μέγιστης πιθανοφάνειας να είναι σταθερός.

Ας υποθέσουμε ότι οι συνθήκες για τη συνοχή του εκτιμητή μέγιστης πιθανοφάνειας είναι ικανοποιημένοι, και

1. θ₀ ∈ εσωτερικό(Θ);
2. f(x | θ) > 0 και είναι δύο φορές συνεχώς διαφορίσιμες στο θ σε κάποια γειτονικά Ν του θ₀;
3. ∫ sup_θ∈N||∇_θf(x | θ)||dx < ∞ και ∫ sup_θ∈N||∇_θθf(x | θ)||dx < ∞;
4. I = E[∇_θln f(x | θ₀) ∇_θln f(x | θ₀)'] υπάρχει και είναι ομαλό;
5. E[sup_θ∈N||∇_θθln f(x | θ)||] < ∞.

Στη συνέχεια, ο εκτιμητής μέγιστης πιθανοφάνειας έχει ασυμπτωτικά κανονική κατανομή:

${\sqrt {n}}{\big (}{\hat {\theta }}_{\mathrm {mle} }-\theta _{0}{\big )}\ {\xrightarrow {d}}\ {\mathcal {N}}(0,\,I^{-1}).$

Απόδειξη, παρακάμπτοντας τις τεχνικές λεπτομέρειες

Μιας και η συνάρτηση λογαριθμικής-πιθανοφάνειας είναι διαφορίσιμη, και το $\theta _{0}$ βρίσκεται στο εσωτερικό του σύνολου παραμέτρων $\Theta$, για το μέγιστο η πρώτη σείρα όρων που θα πρέπει να πληρούνται είναι:

$\nabla _{\!\theta }\,{\hat {\ell }}({\hat {\theta }}\mid x)={\frac {1}{n}}\sum _{i=1}^{n}\nabla _{\!\theta }\ln f(x_{i}\mid {\hat {\theta }})=0.$

Όταν η λογαριθμική-πιθανοφάνεια είναι δύο φορές διαφορίσιμη, η έκφραση αυτή μπορεί να επεκταθεί σε σειρά Taylor γύρω από το σημείο $\theta =\theta _{0}$:

$0={\frac {1}{n}}\sum _{i=1}^{n}\nabla _{\!\theta }\ln f(x_{i}\mid \theta _{0})+{\Bigg [}\,{\frac {1}{n}}\sum _{i=1}^{n}\nabla _{\!\theta \theta }\ln f(x_{i}\mid {\tilde {\theta }})\,{\Bigg ]}({\hat {\theta }}-\theta _{0}),$

οπού ${\tilde {\theta }}$ είναι κάποιο ενδιάμεσο σημείο μεταξύ $\theta _{0}$ και ${\hat {\theta }}$. Από αυτή την έκφραση μπορούμε να συνάγουμε ότι

${\sqrt {n}}({\hat {\theta }}-\theta _{0})={\Bigg [}\,{-{\frac {1}{n}}\sum _{i=1}^{n}\nabla _{\!\theta \theta }\ln f(x_{i}\mid {\tilde {\theta }})}\,{\Bigg ]}^{-1}{\frac {1}{\sqrt {n}}}\sum _{i=1}^{n}\nabla _{\!\theta }\ln f(x_{i}\mid \theta _{0})$

Εδώ η έκφραση στις αγκύλες συγκλίνει με πιθανότητα $H=\mathbb {E} \left[-\nabla _{\theta \theta }\ln f(x|\theta _{0})\right]$ από το νόμο των μεγάλων αριθμών. Το θεώρημα συνεχούς χαρτογράφησης εξασφαλίζει ότι το αντίστροφο αυτής της έκφρασης, επίσης, συγκλίνει με πιθανότητα, στο $H^{-1}$. Το δεύτερο άθρισμα, από το κεντρικό οριακό θεώρημα, συγκλίνει στη διανομή σε μια κανονική πολυμεταβλητή με μέση τιμή μηδέν και πίνακα διακύμανσης ίσο με τις  πληροφορίες Φίσερ $I$. Έτσι, εφαρμόζοντας το θεώρημα του Slutsky σε όλη την έκφραση, προκύπτει ότι το

${\sqrt {n}}({\hat {\theta }}-\theta _{0})\ \ {\xrightarrow {d}}\ \ {\mathcal {N}}{\big (}0,\ H^{-1}IH^{-1}{\big )}.$

Τέλος, η ισότητα πληροφοριών εγγυάται ότι όταν το μοντέλο είναι σωστά καθορισμένο, ο πίνακας $H$ θα είναι ίσος με τον πίνακα πληροφοριών του Φίσερ  $I$, έτσι ώστε η διακύμανση απλοποιείτε απλά στην έκφραση $I^{-1}$.

Παραδείγματα

Διακριτή ομοιόμορφη κατανομή

Σκεφτείτε την περίπτωση όπου n εισιτήρια αριθμημένα από το 1 έως το n , τοποθετούνται σε ένα κουτί και επιλέγεται ένα τυχαία (βλ ομοιόμορφη κατανομή)· έτσι, το μέγεθος του δείγματος είναι 1. Αν n είναι άγνωστο, τότε ο εκτιμητής μέγιστης πιθανοφάνειας ${\hat {n}}$ του n είναι ο αριθμός m για το επιλεχθέν εισιτήριο. (Η πιθανοφάνεια είναι 0 για n < m, 1/n για n ≥ m, και αυτή είναι μεγαλύτερη όταν n = m. Σημειώστε ότι ο εκτιμητής μέγιστης πιθανοφάνειας του n παρουσιάζεται στα κάτω άκρα των πιθανών τιμών {m, m + 1, ...}, και όχι κάπου στη "μέση" του εύρους των πιθανών τιμών, η οποία θα οδηγήσει σε λιγότερο σφάλμα.) Η αναμενόμενη τιμή του αριθμού m για το επιλεχθέν εισιτήριο, και ως εκ τούτου, η αναμενόμενη τιμή του ${\hat {n}}$, είναι (n + 1)/2. Ως αποτέλεσμα, με ένα δείγμα μεγέθους 1, η μέγιστη πιθανότητα εκτιμητής για το n συστηματικά υποτιμούν n (n − 1)/2.

Διακριτή κατανομή, πεπερασμένο παράμετρος χώρο

Ας υποθέσουμε ότι κάποιος επιθυμεί να καθορίσει το σφάλμα ενός άδικου νομίσματος . Ονομάζουμε την πιθανότητα να τύχει ΚΟΡΌΝΑ p. Ο στόχος, στη συνέχεια, γίνεται για να προσδιορίσετε το p.

Ας υποθέσουμε ότι ρίξαμε το νόμισμα 80 φορές: δηλαδή, το δείγμα μπορεί να είναι κάτι σαν x₁ = H, x₂ = T, ..., x₈₀ = T, και η καταμέτρηση του αριθμού των ΚΟΡΟΝΏΝ "H" που παρατηρείται.

Η πιθανότητα να ρίξει ΓΡΆΜΜΑΤΑ είναι 1 − p (εδώ, λοιπόν, p είναι θ ανωτέρω). Ας υποθέσουμε ότι το αποτέλεσμα είναι 49 ΚΟΡΌΝΕΣ και τις 31 ΓΡΆΜΜΑΤΑ, και ας υποθέσουμε ότι το νόμισμα επιλέχτηκε από ένα κουτί που περιέχει τρία νομίσματα: ένα που δίνει ΚΟΡΌΝΑ με πιθανότητα p = 1/3, το οποίο δίνει ΚΟΡΌΝΑ με πιθανότητα p = 1/2 και ένα άλλο που δίνει ΚΟΡΌΝΑ με πιθανότητα p = 2/3. Τα νομίσματα έχουν χάσει τις ετικέτες τους, οπότε δεν γνωρίζουμε ποιο είναι ποιο. Χρησιμοποιώντας τον εκτιμητή μέγιστης πιθανοφάνειας το νόμισμα που έχει τη μεγαλύτερη πιθανοφάνεια μπορεί να βρεθεί, με τα δεδομένα που παρατηρήθηκαν. Χρησιμοποιώντας την συνάρτηση μάζας πιθανότητας της διωνυμικής κατανομής με μέγεθος δείγματος ίσο με το 80,ο αριθμός των επιτυχιών είναι ίσος με 49 αλλά για διαφορετικές τιμές του p (η "πιθανότητα επιτυχίας"), η συνάρτηση πιθανοφάνειας (που ορίζεται παρακάτω), λαμβάνει μία από τις τρεις τιμές:

${\begin{aligned}\Pr(\mathrm {H} =49\mid p=1/3)&={\binom {80}{49}}(1/3)^{49}(1-1/3)^{31}\approx 0.000,\\[6pt]\Pr(\mathrm {H} =49\mid p=1/2)&={\binom {80}{49}}(1/2)^{49}(1-1/2)^{31}\approx 0.012,\\[6pt]\Pr(\mathrm {H} =49\mid p=2/3)&={\binom {80}{49}}(2/3)^{49}(1-2/3)^{31}\approx 0.054.\end{aligned}}$

Η πιθανοφάνεια μεγιστοποιείται όταν p = 2/3, οπότε αυτός είναι ο εκτιμητής μέγιστης πιθανοφάνειας για το.

Διακριτή κατανομή, η συνεχής παράμετρος χώρο

Τώρα, ας υποθέσουμε ότι υπήρχε μόνο ένα νόμισμα, αλλά η p θα μπορούσε να έχει οποιαδήποτε τιμή 0 ≤ p ≤ 1. Η συνάρτηση πιθανοφάνειας για να μεγιστοποιηθεί είναι

$L(p)=f_{D}(\mathrm {H} =49\mid p)={\binom {80}{49}}p^{49}(1-p)^{31},$

και η μεγιστοποίηση είναι πάνω από όλες τις δυνατές τιμές 0 ≤ p ≤ 1.

συνάρτηση πιθανοφάνειας για την αναλογία της αξίας μιας διωνυμικής διαδικασίας         (n = 10)

Ένας τρόπος για να μεγιστοποιηθεί η συνάρτηση αυτή είναι με διαφοροποίηση όσον αφορά το p και ρύθμιση στο μηδέν:

${\begin{aligned}{0}&{}={\frac {\partial }{\partial p}}\left({\binom {80}{49}}p^{49}(1-p)^{31}\right)\\[8pt]&{}=49p^{48}(1-p)^{31}-31p^{49}(1-p)^{30}\\[8pt]&{}=p^{48}(1-p)^{30}\left[49(1-p)-31p\right]\\[8pt]&{}=p^{48}(1-p)^{30}\left[49-80p\right]\end{aligned}}$

η οποία έχει λύσεις, p = 0, p = 1 και p = 49/80. Η λύση που μεγιστοποιεί την πιθανότητα να είναι σαφώς p = 49/80 (αφού p = 0 και p = 1 το αποτέλεσμα στην πιθανοφάνεια του μηδέν). Έτσι, ο εκτιμητής μέγιστης πιθανοφάνειας για το p είναι 49/80.

Το αποτέλεσμα αυτό είναι εύκολα γενικευμένη αντικαθιστώντας ένα γράμμα όπως το t στη θέση 49 για να αντιπροσωπεύει τον παρατηρούμενο αριθμό των "επιτυχιών" της δοκιμής Bernoulli μας, και ένα γράμμα όπως n στη θέση 80, για να αντιπροσωπεύει τον αριθμό των δοκιμών Bernoulli. Ακριβώς το ίδιο για τον υπολογισμό των αποδόσεων, ο εκτιμητής μέγιστης πιθανοφάνειας t / n για κάθε ακολουθία n δοκιμών Bernoulli με αποτέλεσμα t 'επιτυχίες'.

Συνεχής κατανομή, η συνεχής παράμετρος χώρο

Για την κανονική κατανομή ${\mathcal {N}}(\mu ,\sigma ^{2})$ που έχει συνάρτηση πυκνότητας πιθανότητας

$f(x\mid \mu ,\sigma ^{2})={\frac {1}{{\sqrt {2\pi \sigma ^{2}}}\ }}\exp {\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)},$

η αντίστοιχη συνάρτηση πυκνότητας πιθανότητας για ένα δείγμα από n ανεξάρτητες και ισόνομα κατανεμημένες κανονικές τυχαίες μεταβλητές (η πιθανότητα) είναι

$f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma ^{2})=\prod _{i=1}^{n}f(x_{i}\mid \mu ,\sigma ^{2})=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-\mu )^{2}}{2\sigma ^{2}}}\right),$

ή πιο σωστά:

$f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma ^{2})=\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right),$

όπου ${\bar {x}}$ είναι η μέση τιμή του δείγματος.

Αυτή η οικογένεια των κατανομών έχει δύο παραμέτρους: θ = (μ, σ), οπότε μπορούμε να μεγιστοποιήσουμε την πιθανοφάνεια, ${\mathcal {L}}(\mu ,\sigma )=f(x_{1},\ldots ,x_{n}\mid \mu ,\sigma )$, πάνω από δύο παραμέτρους ταυτόχρονα, ή, αν είναι δυνατόν, ξεχωριστά.

Δεδομένου ότι ο λογάριθμος είναι μια συνεχής αυστηρά αυξανόμενη λειτουργία πάνω από το φάσμα της πιθανοφάνειας, οι τιμές που μεγιστοποιούν την πιθανοφάνεια, θα μεγιστοποιήσουν επίσης και τον λογάριθμό του. Αυτή η λογαριθμική πιθανοφάνεια μπορεί να γραφτεί ως εξής:

$\log({\mathcal {L}}(\mu ,\sigma ))=(-n/2)\log(2\pi \sigma ^{2})-{\frac {1}{2\sigma ^{2}}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}$

(Σημείωση: η λογαριθμική-πιθανοφάνεια είναι στενά συνδεδεμένη με τις πληροφορίες εντροπία και τις πληροφορίες Φίσερ.)

Μπορούμε τώρα να υπολογίσουμε τις παραγώγους αυτής της λογαριθμικής-πιθανοφάνειας ως εξής.

${\begin{aligned}0&={\frac {\partial }{\partial \mu }}\log({\mathcal {L}}(\mu ,\sigma ))=0-{\frac {-2n({\bar {x}}-\mu )}{2\sigma ^{2}}}.\end{aligned}}$

Αυτό λύνεται με

${\hat {\mu }}={\bar {x}}=\sum _{i=1}^{n}{\frac {x_{i}}{n}}.$

Αυτό είναι πράγματι το μέγιστο της συνάρτησης, δεδομένου ότι είναι το μόνο σημείο καμπής στο μ και η δεύτερη παράγωγος είναι αυστηρά μικρότερη από το μηδέν. Η αναμενόμενη τιμή είναι ίση με την παράμετρο μ της συγκεκριμένης διανομής,

$E\left[{\widehat {\mu }}\right]=\mu ,\,$

που σημαίνει ότι ο εκτιμητής μέγιστης πιθανοφάνειας ${\widehat {\mu }}$ είναι αμερόληπτος.

Ομοίως μπορούμε να διαφορίσουμε την λογαριθμική πιθανοφάνεια ως προς το σ και είναι ίσο με το μηδέν:

${\begin{aligned}0&={\frac {\partial }{\partial \sigma }}\log \left(\left({\frac {1}{2\pi \sigma ^{2}}}\right)^{n/2}\exp \left(-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right)\right)\\[6pt]&={\frac {\partial }{\partial \sigma }}\left({\frac {n}{2}}\log \left({\frac {1}{2\pi \sigma ^{2}}}\right)-{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{2\sigma ^{2}}}\right)\\[6pt]&=-{\frac {n}{\sigma }}+{\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}+n({\bar {x}}-\mu )^{2}}{\sigma ^{3}}}\end{aligned}}$

το οποίο λύνεται με

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-\mu )^{2}.$

Εισαγωγή της εκτίμησης $\mu ={\widehat {\mu }}$ θα αποκτηθεί από

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{2}-{\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}x_{i}x_{j}.$

Για να υπολογίσουμε την αναμενόμενη τιμή της, είναι βολικό να ξαναγράψουμε την έκφραση σε σχέση με μηδέν-μέσες τυχαίες μεταβλητές (στατιστικό σφάλμα) $\delta _{i}\equiv \mu -x_{i}$. Εκφράζοντας την εκτίμηση σε αυτές τις μεταβλητές αποδόσεις

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}(\mu -\delta _{i})^{2}-{\frac {1}{n^{2}}}\sum _{i=1}^{n}\sum _{j=1}^{n}(\mu -\delta _{i})(\mu -\delta _{j}).$

Απλοποιόντας την έκφραση παραπάνω, αξιοποιώντας τα γεγονότα ότι $E\left[\delta _{i}\right]=0$ και $E[\delta _{i}^{2}]=\sigma ^{2}$ μας επιτρέπει να αποκτήσουμε 

$E\left[{\widehat {\sigma }}^{2}\right]={\frac {n-1}{n}}\sigma ^{2}.$

Αυτό σημαίνει ότι ο εκτιμητής ${\widehat {\sigma }}$ είναι εσφαλμένος. Ωστόσο, ${\widehat {\sigma }}$ είναι σταθερή.

Επίσημα μπορούμε να πούμε ότι ο εκτιμητής μέγιστης πιθανοφάνειας για το $\theta =(\mu ,\sigma ^{2})$ είναι:

${\widehat {\theta }}=\left({\widehat {\mu }},{\widehat {\sigma }}^{2}\right).$

Στην περίπτωση αυτή, οι ΕΜΠ θα μπορούσε να επιτευχθεί ξεχωριστά. Σε γενικές γραμμές, αυτό μπορεί να μην είναι η περίπτωση, και οι ΕΜΠ θα πρέπει να λαμβάνονται ταυτόχρονα.

Η κανονική λογαριθμική πιθανοφάνεια στο μέγιστο παίρνει μια ιδιαίτερα απλή μορφή:

$\log({\mathcal {L}}({\hat {\mu }},{\hat {\sigma }}))={\frac {-n}{2}}(\log(2\pi {\hat {\sigma }}^{2})+1)$

Αυτή η μέγιστη λογαριθμική πιθανοφάνεια μπορεί να αποδειχθεί ότι είναι το ίδιο για πιο γενικότερων ελαχίστων τετραγώνων, ακόμα και για μη-γραμμικά ελάχιστα τετράγωνα. Αυτό συχνά χρησιμοποιείται για τον προσδιορισμό της πιθανοφάνειας με βάση την προσέγγιση του διαστήματος εμπιστοσύνης και τις περιοχές εμπιστοσύνης, οι οποίες είναι γενικά πιο ακριβή από ότι εκείνες που χρησιμοποιούν την ασυμπτωτική κανονικότητα που συζητήθηκε παραπάνω.

Μη-ανεξάρτητες μεταβλητές

Μπορεί να είναι η υπόθεση ότι οι μεταβλητές συσχετίζονται, δηλαδή, δεν είναι ανεξάρτητες. Δύο τυχαίες μεταβλητές X και Y είναι ανεξάρτητες μόνο αν η από κοινού συνάρτηση πυκνότητας πιθανότητας είναι το γινόμενο των επιμέρους συναρτήσεων πυκνότητας πιθανότητας, δηλ.

$f(x,y)=f(x)f(y)\,$

Ας υποθέσουμε ότι κάποιος κατασκευάζει μια σειρά-n Gauss διανυσμάτων από τυχαίες μεταβλητές $(x_{1},\ldots ,x_{n})\,$, όπου κάθε μεταβλητή έχει μέσο που δίνεται από $(\mu _{1},\ldots ,\mu _{n})\,$. Επιπλέον, ας έχουμε τον πίνακα συνδιακύμανσης ότι θα συμβολίζεται με $\Sigma$.

Η κοινή συνάρτηση πυκνότητας πιθανότητας αυτών των n τυχαίων μεταβλητών, στη συνέχεια, δίνεται από:

$f(x_{1},\ldots ,x_{n})={\frac {1}{(2\pi )^{n/2}{\sqrt {{\text{det}}(\Sigma )}}}}\exp \left(-{\frac {1}{2}}\left[x_{1}-\mu _{1},\ldots ,x_{n}-\mu _{n}\right]\Sigma ^{-1}\left[x_{1}-\mu _{1},\ldots ,x_{n}-\mu _{n}\right]^{T}\right)$

$f(x,y)={\frac {1}{2\pi \sigma _{x}\sigma _{y}{\sqrt {1-\rho ^{2}}}}}\exp \left[-{\frac {1}{2(1-\rho ^{2})}}\left({\frac {(x-\mu _{x})^{2}}{\sigma _{x}^{2}}}-{\frac {2\rho (x-\mu _{x})(y-\mu _{y})}{\sigma _{x}\sigma _{y}}}+{\frac {(y-\mu _{y})^{2}}{\sigma _{y}^{2}}}\right)\right]$

Σε αυτό και σε άλλες περιπτώσεις όπου η κοινή συνάρτηση πυκνότητας υπάρχει η συνάρτηση πιθανοφάνειας ορίζεται όπως παραπάνω, στην ενότητα Αρχές, χρησιμοποιώντας αυτή την πυκνότητα.

Επαναληπτικές διαδικασίες

Σκεφτείτε τα προβλήματα που και τα δύο μέλη $x_{i}$ και οι παράμετροι όπως το $\sigma ^{2}$ απαιτούν να εκτιμηθούν. Επαναληπτικές διαδικασίες όπως αλγόριθμοι Προσδοκίας-μεγιστοποίησης μπορούν να χρησιμοποιηθούν για την επίλυση κοινού κατάσταση-εκτίμηση παραμέτρων προβλημάτων.

Για παράδειγμα, ας υποθέσουμε ότι n δείγματα μιας κατάστασης εκτιμούν ${\hat {x}}_{i}$ , μαζί με μια μέση τιμή δείγματος ${\bar {x}}$ έχουν υπολογιστεί είτε από μια ελάχιστη διακύμανση Kalman φίλτρο ή μια ελάχιστη διακύμανση ομαλότερη χρησιμοποιώντας μια προηγούμενη εκτίμηση διακύμανσης ${\widehat {\sigma }}^{2}$. Στη συνέχεια η ημερήσια διακύμανση επαναλαμβάνω μπορεί να ληφθεί από τον υπολογισμό του εκτιμητή μέγιστης πιθανοφάνειας

${\widehat {\sigma }}^{2}={\frac {1}{n}}\sum _{i=1}^{n}({\hat {x}}_{i}-{\bar {x}})^{2}.$

Η σύγκλιση των ΕΜΠ εντός φιλτραρίσματος και η εξομάλυνση των αλγόριθμοι Προσδοκίας (ΑΠ) έχει μελετηθεί στην βιβλιογραφία.

Εφαρμογές

Η εκτίμηση μέγιστης πιθανοφάνειας χρησιμοποιείται για ένα ευρύ φάσμα των στατιστικών μοντέλων, συμπεριλαμβανομένων:

• γραμμικών μοντέλων και γενικευμένων γραμμικών μοντελών
• διερευνητική και επιβεβαιωτική παραγοντική ανάλυση
• δομικά μοντέλα εξισώσεων
  
• πολλές καταστάσεις στο πλαίσιο των έλεγχων υποθέσεων και διαστημάτων εμπιστοσύνης
• διακριτή επιλογή μοντέλων 
• ανίχνευση σήματος (φιλτράρισμα).

Οι χρήσεις αυτές προκύπτουν σε εφαρμογές σε ευρύ σύνολο από τομείς, συμπεριλαμβανομένων:

• συστήματα επικοινωνίας;
• ψυχομετρική;
• οικονομετρία;
• χρονική καθυστέρηση άφιξης (ΧΚΑ) σε ακουστική ή ηλεκτρομαγνητική ανίχνευση
• μοντελοποίηση δεδομένων στην πυρηνική και σωματιδιακή φυσική;
• μαγνητική τομογραφία;
• υπολογιστική φυλογενετική;
• προέλευση/προορισμό και τη διαδρομή-επιλογή μοντέλων σε δίκτυα μεταφορών 
• γεωγραφική δορυφορική-εικονική ταξινόμηση 
• το ηλεκτρικό σύστημα κατάστασης εκτίμησης.

Δείτε επίσης

• Άλλες μέθοδοι εκτίμησης
  • Γενικευμένη μέθοδος των ροπών είναι μέθοδοι που σχετίζονται με την πιθανότητα εξίσωση στην εκτίμηση μέγιστης πιθανοφάνειας.
  • M-εκτιμητής, μια προσέγγιση που χρησιμοποιείται σε ισχυρά στατιστικά στοιχεία.
  • Μέγιστη εκ των υστέρων (MAP) εκτιμητής, για μια αντίθεση με τον τρόπο για τον υπολογισμό εκτιμητών όταν η προγενέστερη γνώση είναι αξιωματική.
  • Μέγιστη εκτίμηση απόστασης, η σχετική μέθοδος αυτή είναι πιο ισχυρή σε πολλές περιπτώσεις.
  • Μέθοδος των ροπών (στατιστικά στοιχεία), μια άλλη δημοφιλής μέθοδος για την εύρεση των παραμέτρων των κατανομών.
  • Μέθοδος στήριξης, μια παραλλαγή της μέγιστης πιθανότητας τεχνική.
  • Εκτίμηση ελάχιστης απόστασης
  • Εκτιμητής Κουάσι-μέγιστης πιθανοφάνειας, ένας ΕΜΠ εκτιμητής που είναι μη εξειδικευμένος, αλλά εξακολουθεί να είναι σταθερός.
  • Περιορισμένη μέγιστη πιθανοφάνεια, μια παραλλαγή χρησιμοποιώντας μια συνάρτηση πιθανότητας που υπολογίζεται από ένα μετασχηματισμένο σύνολο δεδομένων.
• Σχετικές έννοιες:
  • Το BHHH αλγόριθμος είναι μια μη-γραμμική βελτιστοποίηση του αλγορίθμου που είναι δημοφιλής για εκτιμήσεις Μέγιστης Πιθανοφάνειας .
  • Extremum εκτιμητής, μια πιο γενική κλάση των εκτιμητών που ο ΕΜΠ ανήκει.
  • Φίσερ, πληροφορίες,πίνακας πληροφοριών για τη σχέση του με τον πίνακα συνδιακύμανσης ML εκτιμήσεων
  • Λειτουργεία Πιθανοφάνειας, μια περιγραφή σχετικά με το τι συναρτήσεις πιθανότητας υπάρχουν.
  • Μέσου τετραγωνικού σφάλματος, ένα μέτρο του πόσο "καλός" ειναι ενας εκτιμητής της κατανομής της παραμέτρου (είναι ο εκτιμητής μέγιστης πιθανοφάνειας ή κάποιος άλλος εκτιμητής).
  • RANSAC, μια μέθοδος για τον υπολογισμό των παραμέτρων του μαθηματικού μοντέλου δεδομένων που περιέχει ακραίες τιμές
  • Το Rao–Blackwell θεώρημα, ένα αποτέλεσμα, το οποίο παράγει μια διαδικασία για την εύρεση του καλύτερου δυνατού αμερόληπτου εκτιμητή (με την έννοια της έχοντας ελάχιστη μέσου τετραγωνικού σφάλματος). Το ΕΜΠ είναι συχνά ένα καλό σημείο εκκίνησης για τη διαδικασία.
  • Επαρκής στατιστική, η συνάρτηση των δεδομένων, μέσω των οποίων το ΕΜΠ (αν υπάρχει και είναι μοναδικό) θα εξαρτηθεί από τα δεδομένα.

Εξωτερικοί σύνδεσμοι

• Hazewinkel, Michiel, επιμ.. (2001), «Maximum-likelihood method», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/m063100 
• Μέγιστη Πιθανότητα Εκτίμηση Αστάρι (ένα εξαιρετικό σεμινάριο)
• Εφαρμογή MLE για τη δική σας πιθανότητα λειτουργία χρησιμοποιώντας το R
• Μια επιλογή πιθανότητα συναρτήσεις στο R
• «Tutorial on maximum likelihood estimation». Journal of Mathematical Psychology. CiteSeerX: 10.1.1.74.671.