Καμπύλη Ντε Ραμ

Στα μαθηματικά, η καμπύλη Ντε Ραμ είναι ένας συγκεκριμένος τύπος μορφοκλασματικής καμπύλης[2] που ονομάστηκε προς τιμήν του Ζορζ ντε Ραμ[3].
Η συνάρτηση Κάντορ, η καμπύλη Σεζάρο, η συνάρτηση ερωτηματικού του Μινκόφσκι, η Μορφοκλασματική καμπύλη Λεβί, η καμπύλη blancmange και η Νιφάδα του Κοχ αποτελούν ειδικές περιπτώσεις της γενικής καμπύλης Ντε Ραμ[4] .
Κατασκευή
[Επεξεργασία | επεξεργασία κώδικα]Θεωρήστε κάποιον πλήρη μετρικό χώρο (γενικά 2 με τη συνήθη ευκλείδεια απόσταση), και ένα ζεύγος συσταλτών χαρτών στον M:
Σύμφωνα με το θεώρημα σταθερών σημείων του Μπάναχ, αυτά έχουν σταθερά σημεία και αντίστοιχα. Έστω x ένας πραγματικός αριθμός στο διάστημα , που έχει δυαδικό ανάπτυγμα
όπου κάθε είναι 0 ή 1. Έστω ο χάρτης
που ορίζεται από
όπου δηλώνει τη σύνθεση συναρτήσεων. Μπορεί να αποδειχθεί ότι κάθε θα αντιστοιχίσει την κοινή λεκάνη έλξης των και σε ένα μόνο σημείο στο . Η συλλογή των σημείων , που έχει ως παράμετρο μία μόνο πραγματική παράμετρο x, είναι γνωστή ως καμπύλη του Ντε Ραμ.
Ιδιότητες
[Επεξεργασία | επεξεργασία κώδικα]Οι καμπύλες Ντε Ραμ είναι από την κατασκευή τους αυτοομοειδείς, αφού
- για και
- για
Οι αυτοσυμμετρίες όλων των καμπυλών de Rham δίνονται από το μονοειδές που περιγράφει τις συμμετρίες του άπειρου δυαδικού δέντρου ή σύνολο Κάντορ. Αυτό το λεγόμενο μονοειδές διπλής περιόδου είναι ένα υποσύνολο της σπονδυλωτής ομάδας.
Η εικόνα της καμπύλης, δηλαδή το σύνολο των σημείων , μπορεί να ληφθεί από ένα Επαναληπτικό σύστημα συναρτήσεων χρησιμοποιώντας το σύνολο των απεικονίσεων συστολής . Ωστόσο, το αποτέλεσμα ενός επαναληπτικού συστήματος συναρτήσεων με δύο απεικονίσεις συστολής είναι μια καμπύλη Ντε Ραμ αν και μόνο αν οι απεικονίσεις συστολής ικανοποιούν τη συνθήκη συνέχειας.
Λεπτομερή, επεξεργασμένα παραδείγματα της αυτο-ομοιότητας μπορείτε να βρείτε στα άρθρα για τη συνάρτηση Κάντορ και τη συνάρτηση ερωτηματικών του Μινκόφσκι. Ακριβώς το ίδιο μονοειδές αυτοομοιότητας, το δυαδικό μονοειδές, ισχύει για κάθε καμπύλη του Ντε Ραμ.
Ταξινόμηση και παραδείγματα
[Επεξεργασία | επεξεργασία κώδικα]Καμπύλες Σεζάρο
[Επεξεργασία | επεξεργασία κώδικα]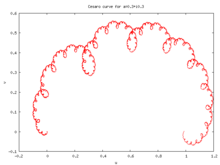

Οι καμπύλες Σεζάρο (ή καμπύλες Σεζάρο-Φάμπερ) είναι καμπύλες Ντε Ραμ που παράγονται από affine μετασχηματισμούς που διατηρούν τον προσανατολισμό, με σταθερά σημεία και .
Εξαιτίας αυτών των περιορισμών, οι καμπύλες Σεζάρο προσδιορίζονται μοναδικά από έναν μιγαδικό αριθμό έτσι ώστε και .
Οι απεικονίσεις συστολής και ορίζονται τότε ως μιγαδικές συναρτήσεις στο μιγαδικό επίπεδο από:
Για την τιμή , η καμπύλη που προκύπτει είναι η Μορφοκλασματική καμπύλη Λεβί.
Καμπύλες Κοχ-Πεάνο
[Επεξεργασία | επεξεργασία κώδικα]

Με παρόμοιο τρόπο, μπορούμε να ορίσουμε την οικογένεια καμπυλών Κοχ – Πεάνο[5] ως το σύνολο των καμπυλών Ντε Ραμ που παράγονται από τους συγγενείς μετασχηματισμούς που αντιστρέφουν τον προσανατολισμό, με σταθερά σημεία και .
Αυτές οι απεικονίσεις εκφράζονται στο μιγαδικό επίπεδο ως συνάρτηση της , της μιγαδικής συζυγούς της :
Το όνομα της οικογένειας προέρχεται από τα δύο πιο διάσημα μέλη της. Η καμπύλη Κοχ προκύπτει από τη ρύθμιση:
ενώ η καμπύλη Πεάνο αντιστοιχεί σε:
Γενικοί affine χάρτες
[Επεξεργασία | επεξεργασία κώδικα]



Οι καμπύλες Σεζάρο-Φάμπερ και Πεάνο-Κοχ είναι και οι δύο ειδικές περιπτώσεις της γενικής περίπτωσης ενός ζεύγους συγγενών γραμμικών μετασχηματισμών στο μιγαδικό επίπεδο. Καθορίζοντας το ένα τελικό σημείο της καμπύλης στο 0 και το άλλο στο ένα, η γενική περίπτωση προκύπτει με επανάληψη των δύο μετασχηματισμών
και
Καθώς είναι μετασχηματισμοί affine, οι μετασχηματισμοί αυτοί δρουν σε ένα σημείο του δισδιάστατου επιπέδου δρώντας στο διάνυσμα
Το μέσο της καμπύλης βρίσκεται στο σημείο - οι άλλες τέσσερις παράμετροι μπορούν να μεταβληθούν για τη δημιουργία μιας μεγάλης ποικιλίας καμπυλών.
Η Καμπύλη blancmange της παραμέτρου μπορεί να ληφθεί θέτοντας , και . Δηλαδή:
και
Δεδομένου ότι η καμπύλη blancmange της παραμέτρου είναι η παραβολή της εξίσωσης , αυτό καταδεικνύει το γεγονός ότι σε ορισμένες περιπτώσεις, οι καμπύλες Ντε Ραμ μπορεί να είναι ομαλές.
Συνάρτηση ερωτηματικών του Μινκόφσκι
[Επεξεργασία | επεξεργασία κώδικα]Η συνάρτηση ερωτηματικού του Μινκόφσκι[6] παράγεται από το ζεύγος χαρτών
και
Γενικεύσεις
[Επεξεργασία | επεξεργασία κώδικα]Είναι εύκολο να γενικεύσουμε τον ορισμό χρησιμοποιώντας περισσότερες από δύο απεικονίσεις συστολής. Εάν χρησιμοποιούνται n απεικονίσεις, τότε πρέπει να χρησιμοποιηθεί η n'-αρχική διάσπαση του x αντί της δυαδικής επέκτασης των πραγματικών αριθμών. Η συνθήκη συνέχειας πρέπει να γενικευτεί σε:
- , for
Αυτή η συνθήκη συνέχειας μπορεί να γίνει κατανοητή με το ακόλουθο παράδειγμα. Ας υποθέσουμε ότι κάποιος εργάζεται στη βάση 10. Τότε έχουμε (ως γνωστόν) ότι 0,999...= 1,000... που είναι μια εξίσωση συνέχειας που πρέπει να εφαρμόζεται σε κάθε τέτοιο κενό. Δηλαδή, δεδομένων των δεκαδικών ψηφίων με , έχουμε
Μια τέτοια γενίκευση επιτρέπει, για παράδειγμα, την παραγωγή της καμπύλης βέλους Σιερπινσκι (της οποίας η εικόνα είναι το Τρίγωνο Σιερπίνσκι), χρησιμοποιώντας τις απεικονίσεις συστολής ενός συστήματος επαναληπτικών συναρτήσεων που παράγει το Τρίγωνο Σιερπίνσκι.
Πολλαπλές καμπύλες
[Επεξεργασία | επεξεργασία κώδικα]Ο Ορνστάιν και άλλοι περιγράφουν ένα πολυμορφοκλασματικό σύστημα[7], όπου αντί να λειτουργεί κανείς σε μια σταθερή βάση, δουλεύει σε μια μεταβλητή βάση.
Θεωρήστε το χώρο του γινομένου των διακριτών χώρων μεταβλητής βάσης-.
για την κυκλική ομάδα, για έναν ακέραιο αριθμό. Κάθε πραγματικός αριθμός στο μοναδιαίο διάστημα μπορεί να αναπτυχθεί σε μια ακολουθία έτσι ώστε κάθε . Πιο συγκεκριμένα, ένας πραγματικός αριθμός γράφεται ως εξής
Αυτή η επέκταση δεν είναι μοναδική, αν όλα τα περάσουν από κάποιο σημείο . Σε αυτή την περίπτωση, έχουμε ότι
Τέτοια σημεία είναι ανάλογα με τις δυαδικές λογικές στο δυαδικό ανάπτυγμα, και οι εξισώσεις συνέχειας στην καμπύλη πρέπει να εφαρμοστούν σε αυτά τα σημεία.
Για κάθε , πρέπει να προσδιορίσουμε δύο πράγματα: ένα σύνολο δύο σημείων και και ένα σύνολο συναρτήσεων (με ). Η συνθήκη συνέχειας είναι τότε όπως παραπάνω,
- , for
Το αρχικό παράδειγμα του Ορνστάιν χρησιμοποιούσε
Δημοσιεύσεις
[Επεξεργασία | επεξεργασία κώδικα]- Georges de Rham, On Some Curves Defined by Functional Equations (1957), reprinted in Classics on Fractals, ed. Gerald A. Edgar (Addison-Wesley, 1993), pp. 285–298.
- Georges de Rham, Sur quelques courbes definies par des equations fonctionnelles. Univ. e Politec. Torino. Rend. Sem. Mat., 1957, 16, 101 –113
- Linas Vepstas, A Gallery of de Rham curves, (2006).
- Linas Vepstas, Symmetries of Period-Doubling Maps, (2006). (A general exploration of the modular group symmetry in fractal curves.)
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]- Αλγόριθμος διαμαντιού τετραγώνου
- Καμπύλη που γεμίζει το χώρο
- Νιφάδα του Κοχ
- Καμπύλη Χίλμπερτ
- Καμπύλη του δράκου
- Σπόγγος του Μένγκερ
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Novikov (mathématicien).), Igor Iakovlevič· Protasov, Vladimir I︠U︡rʹevich (2011). Wavelet Theory. American Mathematical Soc. ISBN 978-0-8218-4984-2.
- ↑ Novikov (mathématicien).), Igor Iakovlevič· Protasov, Vladimir I︠U︡rʹevich (2011). Wavelet Theory. American Mathematical Soc. ISBN 978-0-8218-4984-2.
- ↑ «Georges de Rham - Biography». Maths History (στα Αγγλικά). Ανακτήθηκε στις 11 Δεκεμβρίου 2023.
- ↑ Lava, Paolo Pietro· Balzarotti, Giorgio (3 Ιουλίου 2013). 103 curiosità matematiche: Teoria dei numeri, delle cifre e delle relazioni nella matematica contemporanea. HOEPLI EDITORE. ISBN 978-88-203-5804-4.
- ↑ Bovill, Carl (11 Μαρτίου 2013). Fractal Geometry in Architecture and Design. Springer Science & Business Media. ISBN 978-1-4612-0843-3.
- ↑ Finch, Steven R. (18 Αυγούστου 2003). Mathematical Constants. Cambridge University Press. ISBN 978-0-521-81805-6.
- ↑ Tirapegui, E.· Martínez, Javier (6 Δεκεμβρίου 2012). Instabilities and Nonequilibrium Structures VI. Springer Science & Business Media. ISBN 978-94-011-4247-2.







![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)











![{\displaystyle x\in [0,1/2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d93a243e1a2d9b69eb484b0838348d4756ab37d7)

![{\displaystyle x\in [1/2,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd84edce0132fcd4f173b087f205d75048fc3643)
![{\displaystyle \{p(x),x\in [0,1]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bf309cbaa841af0f39085b42b33785e9dcc4719)





















































