Συνάρτηση Κάντορ

Το γράφημα της συνάρτησης Κάντορ στο μοναδιαίο διάστημα

Στα μαθηματικά, η συνάρτηση Κάντορ είναι ένα παράδειγμα συνάρτησης που είναι συνεχής, αλλά όχι απολύτως συνεχής. Είναι ένα διαβόητο αντιπαράδειγμα στην ανάλυση, επειδή αμφισβητεί τις αφελείς διαισθήσεις σχετικά με τη συνέχεια, την παράγωγο και το μέτρο. Παρότι είναι συνεχής παντού και η παράγωγος της είναι μηδέν σχεδόν παντού, η τιμή της πηγαίνει πάντα από το 0 στο 1 όταν το όρισμά της πηγαίνει από το 0 στο 1. Έτσι, από μια άποψη η συνάρτηση μοιάζει πολύ με μια σταθερή συνάρτηση που δεν μπορεί να αυξηθεί, και από μια άλλη άποψη αυξάνεται μονοτονικά.

Είναι επίσης γνωστή ως τριπλή συνάρτηση του Κάντορ, συνάρτηση του Λεμπέσγκ , μοναδική συνάρτηση του Λεμπέσγκ, συνάρτηση του Κάντορ-Βιτάλι, σκάλα του διαβόλου, συνάρτηση της σκάλας του Κάντορ και συνάρτηση των Κάντορ-Λεμπέσγκ . Ο Γκέοργκ Κάντορ (1884) εισήγαγε τη συνάρτηση Κάντορ και ανέφερε ότι ο Σέφερ είχε επισημάνει ότι αποτελούσε αντιπαράδειγμα σε μια επέκταση του θεμελιώδους θεωρήματος του λογισμού που ισχυρίστηκε ο Χάρνακ. Η συνάρτηση Κάντορ συζητήθηκε και διαδόθηκε από τον Σίφερ (1884), τον Λεμπέσγκ (1904) και τον Βιτάλι (1905).

Ορισμός

Επαναληπτική κατασκευή της συνάρτησης Κάντορ

Για να ορίσουμε τη συνάρτηση Κάντορ $c:[0,1]\to [0,1]$, έστω $x$ οποιοσδήποτε αριθμός στο $[0,1]$ και λαμβάνουμε $c(x)$ με τα ακόλουθα βήματα:

1. Να εκφραστεί το $x$ στη βάση 3.
2. Αν η αναπαράσταση του $x$ στη βάση 3 περιέχει ένα 1, αντικαθιστούμε κάθε ψηφίο αυστηρά μετά το πρώτο 1 με 0.
3. Αντικαθιστούμε όλα τα υπόλοιπα 2s με 1s.
4. Ερμηνεύουμε το αποτέλεσμα ως δυαδικό αριθμό. Το αποτέλεσμα είναι $c(x)$.

Ενδεικτικά:

• ${\tfrac {1}{4}}$ έχει την τριμερή αναπαράσταση 0.02020202... Δεν υπάρχουν 1, οπότε το επόμενο στάδιο εξακολουθεί να είναι 0.02020202... Αυτό ξαναγράφεται ως 0.01010101... Αυτή είναι η δυαδική αναπαράσταση του ${\tfrac {1}{3}}$, οπότε$c({\tfrac {1}{4}})={\tfrac {1}{3}}$.
• ${\tfrac {1}{5}}$ έχει την τριμερή αναπαράσταση 0.01210121... Τα ψηφία μετά το πρώτο 1 αντικαθίστανται από 0 για να παραχθεί το 0.01000000... Αυτό δεν ξαναγράφεται αφού δεν έχει 2. Αυτή είναι η δυαδική αναπαράσταση του ${\tfrac {1}{4}}$, οπότε $c({\tfrac {1}{5}})={\tfrac {1}{4}}$.
• ${\tfrac {200}{243}}$ έχει την τριμερή αναπαράσταση 0,21102 (ή 0,211012222...). Τα ψηφία μετά το πρώτο 1 αντικαθίστανται από 0 για να προκύψει το 0,21. Αυτό ξαναγράφεται ως 0,11. Αυτή είναι η δυαδική αναπαράσταση του ${\tfrac {3}{4}}$, οπότε $c({\tfrac {200}{243}})={\tfrac {3}{4}}$.

Ισοδύναμα, αν <${\mathcal {C}}$ είναι το σύνολο Κάντορ στο [0,1], τότε η συνάρτηση Κάντορ $c:[0,1]\to [0,1]$ μπορεί να οριστεί ως εξής

$c(x)={\begin{cases}\sum _{n=1}^{\infty }{\frac {a_{n}}{2^{n}}},&x=\sum _{n=1}^{\infty }{\frac {2a_{n}}{3^{n}}}\in {\mathcal {C}}\ \mathrm {for} \ a_{n}\in \{0,1\};\\\sup _{y\leq x,\,y\in {\mathcal {C}}}c(y),&x\in [0,1]\smallsetminus {\mathcal {C}}.\end{cases}}$

Αυτός ο τύπος είναι καλά προσδιορισμένος, δεδομένου ότι κάθε μέλος του συνόλου Κάντορ έχει μια μοναδική βάση, αφού κάθε μέλος του συνόλου Κάντορ έχει μια μοναδική αναπαράσταση στη βάση 3 που περιέχει μόνο τα ψηφία 0 ή 2. (Για ορισμένα μέλη του ${\mathcal {C}}$, το τριμερές ανάπτυγμα είναι επαναλαμβανόμενο με τα 2 στο τέλος και υπάρχει ένα εναλλακτικό μη επαναλαμβανόμενο ανάπτυγμα που τελειώνει σε 1. Παραδείγματος χάριν, ${\tfrac {1}{3}}$ = 0.1₃ = 0.13 = 0.02222...₃ είναι μέλος του συνόλου Κάντορ). Αφού $c(0)=0$ και $c(1)=1$, και το $c$ είναι μονοτονικό στο ${\mathcal {C}}$, είναι σαφές ότι $0\leq c(x)\leq 1$ ισχύει επίσης για όλα $x\in [0,1]\smallsetminus {\mathcal {C}}$.

Ιδιότητες

Η συνάρτηση Κάντορ αμφισβητεί τις αφελείς διαισθήσεις σχετικά με τη συνέχεια και το μέτρο- αν και είναι συνεχής παντού και έχει μηδενική παράγωγο σχεδόν παντού, ${\textstyle c(x)}$ πηγαίνει από το 0 στο 1 καθώς το ${\textstyle x}$ πηγαίνει από το 0 στο 1, και παίρνει κάθε ενδιάμεση τιμή. Η συνάρτηση Κάντορ είναι το πιο συχνά αναφερόμενο παράδειγμα μιας πραγματικής συνάρτησης που είναι ομοιόμορφα συνεχής ( συγκεκριμένα, είναι συνεχής κατά Χόλντερ με εκθέτη α = log 2/log 3) αλλά όχι απόλυτα συνεχής. Είναι σταθερή σε διαστήματα της μορφής (0.x₁x₂x₃...x_n022222..., 0.x₁x₂x₃...x_n200000...), και κάθε σημείο που δεν βρίσκεται στο σύνολο Κάντορ βρίσκεται σε ένα από αυτά τα διαστήματα, οπότε η παράγωγος της είναι 0 εκτός του συνόλου Κάντορ. Από την άλλη πλευρά, δεν έχει παράγωγο σε κανένα σημείο σε ένα μη μετρήσιμο υποσύνολο του συνόλου Κάντορ που περιέχει τα τελικά σημεία των διαστημάτων που περιγράφηκαν παραπάνω.

Η συνάρτηση Κάντορ μπορεί επίσης να θεωρηθεί ως η αθροιστική συνάρτηση κατανομής πιθανότητας του μέτρου μ του 1/2-1/2 Μπερνούλι που υποστηρίζεται στο σύνολο Κάντορ: ${\textstyle c(x)=\mu ([0,x])}$. Αυτή η κατανομή πιθανότητας, που ονομάζεται κατανομή Κάντορ, δεν έχει διακριτό μέρος. Δηλαδή, το αντίστοιχο μέτρο δεν έχει άτομα. Για το λόγο αυτό δεν υπάρχουν ασυνέχειες άλματος στη συνάρτηση- κάθε τέτοιο άλμα θα αντιστοιχούσε σε ένα άτομο στο μέτρο.

Παρά ταύτα, κανένα μη σταθερό μέρος της συνάρτησης Κάντορ δεν μπορεί να αναπαρασταθεί ως ολοκλήρωμα μιας συνάρτησης πυκνότητας πιθανότητας- η ολοκλήρωση οποιασδήποτε υποτιθέμενης συνάρτησης πυκνότητας πιθανότητας που δεν είναι σχεδόν παντού μηδέν σε οποιοδήποτε διάστημα θα δώσει θετική πιθανότητα σε κάποιο διάστημα στο οποίο η κατανομή αυτή αποδίδει πιθανότητα μηδέν. Ειδικότερα, όπως επεσήμανε ο Βιτάλι (1905), η συνάρτηση δεν είναι το ολοκλήρωμα της παραγώγου της ακόμη και αν η παράγωγος υπάρχει σχεδόν παντού.

Η συνάρτηση Κάντορ είναι το τυπικό παράδειγμα μιας μοναδικής συνάρτησης.

Η συνάρτηση Κάντορ είναι μη φθίνουσα, και έτσι ειδικότερα η γραφική της παράσταση ορίζει μια ορθοκανονική καμπύλη. Ο Σίφερ (1884) έδειξε ότι το μήκος τόξου της γραφικής της παράστασης είναι 2. Να σημειωθεί ότι η γραφική παράσταση οποιασδήποτε μη φθίνουσας συνάρτησης τέτοιας ώστε $f(0)=0$ και $f(1)=1$ έχει μήκος όχι μεγαλύτερο από 2. Με αυτή την έννοια, η συνάρτηση Κάντορ είναι ακραία.

Έλλειψη απόλυτης συνέχειας

Επειδή το μέτρο Λεμπέσγκ του αμέτρητου άπειρου συνόλου Κάντορ είναι 0, για κάθε θετικό ε < 1 και δ, υπάρχει μια πεπερασμένη ακολουθία διαζευγμένων κατά ζεύγη υποδιαστημάτων με συνολικό μήκος < δ, κατά την οποία η συνάρτηση Κάντορ αυξάνεται αθροιστικά περισσότερο από ε.

Στην πραγματικότητα, για κάθε δ > 0 υπάρχουν πεπερασμένα πολλά κατά ζεύγη διαστήματα που δεν συνδέονται μεταξύ τους (x_k,y_k) (1 ≤ k ≤ M) με $\sum \limits _{k=1}^{M}(y_{k}-x_{k})<\delta$ και $\sum \limits _{k=1}^{M}(c(y_{k})-c(x_{k}))=1$.

Εναλλακτικοί ορισμοί

Επαναληπτική κατασκευή

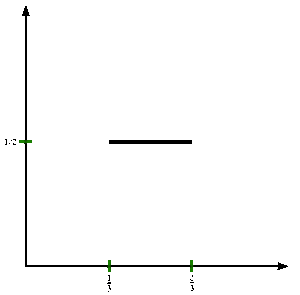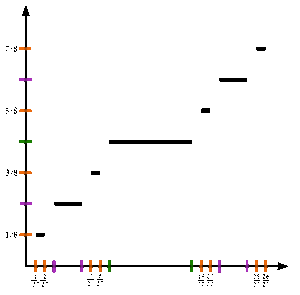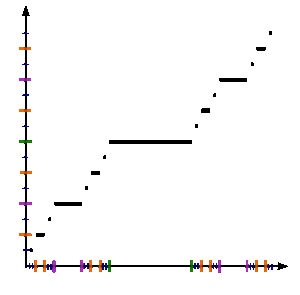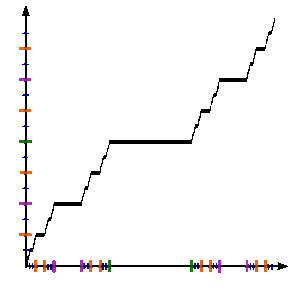
Παρακάτω ορίζουμε μια ακολουθία {f_n} συναρτήσεων στο μοναδιαίο διάστημα που συγκλίνει στη συνάρτηση του Κάντορ.

Έστω f₀(x) = x.

Τότε, για κάθε ακέραιο n ≥ 0, η επόμενη συνάρτηση f_n+1(x) θα ορίζεται ως προς την f_n(x) ως εξής:

Έστω f_n+1(x) = 1/2 × f_n(3x),  όταν 0 ≤ x ≤ 1/3 ;

Έστω f_n+1(x) = 1/2,  όταν 1/3 ≤ x ≤ 2/3 ;

Έστω f_n+1(x) = 1/2 + 1/2 × f_n(3 x − 2),  όταν 2/3 ≤ x ≤ 1.

Οι τρεις ορισμοί είναι συμβατοί στα τελικά σημεία 1/3 και 2/3, επειδή f_n(0) = 0 και f_n(1) = 1 για κάθε n, με επαγωγή. Μπορεί κανείς να ελέγξει ότι η f_n συγκλίνει σημειακά στη συνάρτηση Κάντορ που ορίστηκε παραπάνω. Επιπλέον, η σύγκλιση είναι ομοιόμορφη. Πράγματι, διαχωρίζοντας σε τρεις περιπτώσεις, σύμφωνα με τον ορισμό της f_n+1, βλέπουμε ότι

$\max _{x\in [0,1]}|f_{n+1}(x)-f_{n}(x)|\leq {\frac {1}{2}}\,\max _{x\in [0,1]}|f_{n}(x)-f_{n-1}(x)|,\quad n\geq 1.$

Αν f συμβολίζει την οριακή συνάρτηση, προκύπτει ότι, για κάθε n ≥ 0,

$\max _{x\in [0,1]}|f(x)-f_{n}(x)|\leq 2^{-n+1}\,\max _{x\in [0,1]}|f_{1}(x)-f_{0}(x)|.$

Επίσης, η επιλογή της αρχικής συνάρτησης δεν έχει σημασία, εφόσον f₀(0) = 0, f₀(1) = 1 και f₀ είναι περιορισμένη.

Μορφοκλασματικός όγκος

Η συνάρτηση Κάντορ είναι στενά συνδεδεμένη με το σύνολο Κάντορ. Το σύνολο Κάντορ C μπορεί να οριστεί ως το σύνολο εκείνων των αριθμών στο διάστημα [0, 1] που δεν περιέχουν το ψηφίο 1 στο ανάπτυγμά τους στη βάση 3 (τριαδική), εκτός αν το 1 ακολουθείται μόνο από μηδενικά (οπότε η ουρά 1000$\ldots$ μπορεί να αντικατασταθεί από 0222$\ldots$ για να απαλλαγούμε από οποιοδήποτε 1). Αποδεικνύεται ότι το σύνολο Κάντορ είναι ένα φράκταλ με (αναρίθμητα) άπειρα σημεία (μηδενικός όγκος), αλλά μηδενικό μήκος (μονοδιάστατος όγκος). Μόνο ο D-διάστατος όγκος $H_{D}$ (με την έννοια ενός μέτρου Χάουστορφ) αποκτά πεπερασμένη τιμή, όπου $D=\log(2)/\log(3)$ είναι η διάσταση φράκταλ του C. Μπορούμε να ορίσουμε εναλλακτικά τη συνάρτηση Κάντορ ως τον D-διάστατο όγκο των τμημάτων του συνόλου Κάντορ

$f(x)=H_{D}(C\cap (0,x)).$

Αυτοομοιότητα

Η συνάρτηση Κάντορ διαθέτει αρκετές συμμετρίες. Για $0\leq x\leq 1$, υπάρχει μια συμμετρία ανάκλασης

$c(x)=1-c(1-x)$

και ένα ζεύγος μεγεθύνσεων, μία αριστερά και μία δεξιά:

$c\left({\frac {x}{3}}\right)={\frac {c(x)}{2}}$

και

$c\left({\frac {x+2}{3}}\right)={\frac {1+c(x)}{2}}$

Οι μεγεθύνσεις μπορούν να κλιμακωθούν- δημιουργούν το δυαδικό μονοειδές. Αυτό παρουσιάζεται με τον ορισμό διαφόρων βοηθητικών συναρτήσεων. Ορισμός της αντανάκλασης ως

$r(x)=1-x$

Η πρώτη αυτοσυμμετρία μπορεί να εκφραστεί ως εξής

$r\circ c=c\circ r$

όπου το σύμβολο $\circ$ δηλώνει τη σύνθεση συναρτήσεων. Δηλαδή, $(r\circ c)(x)=r(c(x))=1-c(x)$ και ομοίως για τις άλλες περιπτώσεις. Για την αριστερή και τη δεξιά μεγέθυνση, γράφουμε τις αριστερές απεικονίσεις

$L_{D}(x)={\frac {x}{2}}$ και $L_{C}(x)={\frac {x}{3}}$

Τότε η συνάρτηση Κάντορ υπακούει στην

$L_{D}\circ c=c\circ L_{C}$

Ομοίως, ορίζονται οι δεξιές αντιστοιχίσεις ως εξής

$R_{D}(x)={\frac {1+x}{2}}$ and $R_{C}(x)={\frac {2+x}{3}}$

Τότε, επίσης,

$R_{D}\circ c=c\circ R_{C}$

Οι δύο πλευρές μπορούν να αντικατοπτρίζονται η μία πάνω στην άλλη.

$L_{D}\circ r=r\circ R_{D}$

και παρομοίως,

$L_{C}\circ r=r\circ R_{C}$

Αυτές οι πράξεις μπορούν να στοιβάζονται αυθαίρετα. Ας δούμε, παραδείγματος χάριν, την ακολουθία των κινήσεων αριστερά-δεξιά $LRLLR.$ Προσθέτοντας τους δείκτες C και D, και, για λόγους σαφήνειας, αφήνοντας τον τελεστή σύνθεσης $\circ$ σε όλα τα σημεία εκτός από λίγα, έχουμε:

$L_{D}R_{D}L_{D}L_{D}R_{D}\circ c=c\circ L_{C}R_{C}L_{C}L_{C}R_{C}$

Οι αυθαίρετες συμβολοσειρές πεπερασμένου μήκους στα γράμματα L και R αντιστοιχούν στους δυαδικούς ορθολογισμούς, δεδομένου ότι κάθε δυαδικός ορθολογισμός μπορεί να γραφεί τόσο ως $y=n/2^{m}$ για ακέραιους n και m όσο και ως πεπερασμένο μήκος bits $y=0.b_{1}b_{2}b_{3}\cdots b_{m}$ με $b_{k}\in \{0,1\}.$ Έτσι, κάθε δυαδική λογική βρίσκεται σε ένα προς ένα αντιστοιχία με κάποια αυτοσυμμετρία της συνάρτησης Κάντορ.

Κάποιες σημειολογικές ανακατατάξεις μπορούν να κάνουν τα παραπάνω ελαφρώς ευκολότερα στην έκφρασή τους. Έστω $g_{0}$ και $g_{1}$ για τα L και R. Η σύνθεση συναρτήσεων επεκτείνει αυτό σε ένα μονοειδές, με την έννοια ότι μπορεί κανείς να γράψει $g_{010}=g_{0}g_{1}g_{0}$ και γενικά, $g_{A}g_{B}=g_{AB}$ για κάποιες δυαδικές σειρές ψηφίων A, B, όπου AB είναι απλά η συνηθισμένη συνένωση τέτοιων σειρών. Το δυαδικό μονοειδές M είναι τότε το μονοειδές όλων αυτών των πεπερασμένου μήκους κινήσεων αριστερά-δεξιά. Γράφοντας $\gamma \in M$ ως ένα γενικό στοιχείο του μονοειδούς, υπάρχει μια αντίστοιχη αυτοσυμμετρία της συνάρτησης Κάντορ:

$\gamma _{D}\circ c=c\circ \gamma _{C}$

Το ίδιο το δυαδικό μονοειδές έχει αρκετές ενδιαφέρουσες ιδιότητες. Μπορεί να θεωρηθεί ως ένας πεπερασμένος αριθμός κινήσεων αριστερά-δεξιά σε ένα άπειρο δυαδικό δέντρο- τα άπειρα απομακρυσμένα "φύλλα" στο δέντρο αντιστοιχούν στα σημεία του συνόλου Κάντορ, και έτσι, το μονοειδές αναπαριστά επίσης τις αυτοσυμμετρίες του συνόλου Κάντορ. Πράγματι, μια μεγάλη κατηγορία συχνά εμφανιζόμενων φράκταλ περιγράφεται από το δυαδικό μονοειδές- πρόσθετα παραδείγματα μπορείτε να βρείτε στο άρθρο για τις καμπύλες του ντε Ραμ. Άλλα φράκταλ που διαθέτουν αυτοομοιότητα περιγράφονται με άλλα είδη μονοειδών. Το δυαδικό μονοειδές είναι το ίδιο ένα υπομονοειδές της σπονδυλωτής ομάδας $SL(2,\mathbb {Z} ).$

Σημειώστε ότι η συνάρτηση Κάντορ έχει κάτι περισσότερο από μια περαστική ομοιότητα με τη συνάρτηση ερωτηματικών του Μινκόφσκι. Συγκεκριμένα, υπακούει στις ίδιες ακριβώς σχέσεις συμμετρίας, αν και σε τροποποιημένη μορφή.

Γενικεύσεις

Έστω

$y=\sum _{k=1}^{\infty }b_{k}2^{-k}$

να είναι το dyadic (δυαδικό) ανάπτυγμα του πραγματικού αριθμού 0 ≤ y ≤ 1 ως προς τα δυαδικά ψηφία b_k ∈ {0,1}. Το ανάπτυγμα αυτό αναλύεται λεπτομερέστερα στο άρθρο για τον δυαδικό μετασχηματισμό. Στη συνέχεια, θεωρήστε τη συνάρτηση

$C_{z}(y)=\sum _{k=1}^{\infty }b_{k}z^{k}.$

Για z = 1/3, το αντίστροφο της συνάρτησης x = 2 C_1/3(y) είναι η συνάρτηση Κάντορ. Δηλαδή, y = y(x) είναι η συνάρτηση Κάντορ. Γενικά, για οποιοδήποτε z < 1/2, C_z(y) μοιάζει με τη συνάρτηση Κάντορ γυρισμένη στο πλάι, με το πλάτος των βημάτων να γίνεται μεγαλύτερο καθώς το z πλησιάζει το μηδέν.

Όπως αναφέρθηκε παραπάνω, η συνάρτηση Κάντορ είναι επίσης η αθροιστική συνάρτηση κατανομής ενός μέτρου στο σύνολο Κάντορ. Διαφορετικές συναρτήσεις Κάντορ, ή Σκάλες του Διαβόλου, μπορούν να προκύψουν εξετάζοντας διαφορετικά μέτρα πιθανότητας χωρίς άτομα που υποστηρίζονται στο σύνολο Κάντορ ή σε άλλα φράκταλ. Ενώ η συνάρτηση Κάντορ έχει παράγωγο 0 σχεδόν παντού, η τρέχουσα έρευνα επικεντρώνεται στο ερώτημα του μεγέθους του συνόλου των σημείων όπου η άνω δεξιά παράγωγος διαφέρει από την κάτω δεξιά παράγωγο, προκαλώντας την ανυπαρξία της παραγώγου. Αυτή η ανάλυση της διαφοροποιησιμότητας δίνεται συνήθως σε όρους διάστασης του φράκταλ, με τη διάσταση Χάουστορφ η πιο δημοφιλής επιλογή. Αυτή η ερευνητική γραμμή ξεκίνησε τη δεκαετία του 1990 από τον Νταρστ,ο οποίος έδειξε ότι η διάσταση Χάουστορφ του συνόλου της μη διαφορισιμότητας της συνάρτησης Κάντορ είναι το τετράγωνο της διάστασης του συνόλου Κάντορ, $(\log 2/\log 3)^{2}$. Στη συνέχεια ο Φαλκόνερ έδειξε ότι αυτή η σχέση τετραγωνισμού ισχύει για όλα τα κανονικά, μοναδιαία μέτρα του Άλφορ, δηλ.

$$\dim _{H}\left\{x:f'(x)=\lim _{h\to 0^{+}}{\frac {\mu ([x,x+h])}{h}}{\text{ does not exist}}\right\}=\left(\dim _{H}\operatorname {supp} (\mu )\right)^{2}$$

Αργότερα, ο Τροσάιτ αποκτά μια πιο ολοκληρωμένη εικόνα του συνόλου όπου η παράγωγος δεν υπάρχει για πιο γενικά κανονικοποιημένα μέτρα του Γκιμπ που υποστηρίζονται σε αυτοομοειδή σύνολα.

Η συνάρτηση ερωτηματικού του Χέρμαν Μινκόφσκι μοιάζει οπτικά με τη συνάρτηση Κάντορ, καθώς εμφανίζεται ως μια "εξομαλυμένη" μορφή της τελευταίας- μπορεί να κατασκευαστεί περνώντας από ένα συνεχές ανάπτυγμα κλάσματος σε ένα δυαδικό ανάπτυγμα, όπως ακριβώς η συνάρτηση Κάντορ μπορεί να κατασκευαστεί περνώντας από ένα τριμερές ανάπτυγμα σε ένα δυαδικό ανάπτυγμα. Η συνάρτηση ερωτηματικού έχει την ενδιαφέρουσα ιδιότητα να διαθέτει εξαφανιζόμενες παραγώγους σε όλους τους ρητούς αριθμούς.

Δείτε επίσης

• Χαλί του Σιερπίνσκι
• Φτέρη του Μπάρνσλεϊ
• Νιφάδα του Κοχ
• Καμπύλη Χίλμπερτ
• Καμπύλη του δράκου
• Σπόγγος του Μένγκερ

• Σύνολο Μάντελμπροτ
• Σύνολο Julia
• Οικοδομήσιμο Σύμπαν

Βιβλιογραφία

• Bass, Richard Franklin (2013) [2011]. Real analysis for graduate students (Second έκδοση). Createspace Independent Publishing. ISBN 978-1-4818-6914-0. 
• Cantor, G. (1884). «De la puissance des ensembles parfaits de points: Extrait d'une lettre adressée à l'éditeur». Acta Mathematica (International Press of Boston) 4: 381–392. doi:10.1007/bf02418423. ISSN 0001-5962.  Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
• Darst, Richard B.; Palagallo, Judith A.; Price, Thomas E. (2010), Curious curves, Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6 
• Dovgoshey, O.; Martio, O.; Ryazanov, V.; Vuorinen, M. (2006). «The Cantor function». Expositiones Mathematicae (Elsevier BV) 24 (1): 1–37. doi:10.1016/j.exmath.2005.05.002. ISSN 0723-0869. MR 2195181. 
• Fleron, Julian F. (1994-04-01). «A Note on the History of the Cantor Set and Cantor Function». Mathematics Magazine (Informa UK Limited) 67 (2): 136–140. doi:10.2307/2690689. ISSN 0025-570X. https://archive.org/details/sim_mathematics-magazine_1994-04_67_2/page/136. 
• Lebesgue, H. (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Paris: Gauthier-Villars 
• Leoni, Giovanni (2017). A first course in Sobolev spaces. 181 (2nd έκδοση). Providence, Rhode Island: American Mathematical Society. σελ. 734. ISBN 978-1-4704-2921-8. OCLC 976406106. 
• Scheeffer, Ludwig (1884). «Allgemeine Untersuchungen über Rectification der Curven». Acta Mathematica (International Press of Boston) 5: 49–82. doi:10.1007/bf02421552. ISSN 0001-5962. 
• Thomson, Brian S.· Bruckner, Judith B.· Bruckner, Andrew M. (2008) [2001]. Elementary real analysis (Second έκδοση). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8. 
• Vestrup, E.M. (2003). The theory of measures and integration. Wiley series in probability and statistics. John Wiley & sons. ISBN 978-0471249771. 
• Vitali, A. (1905), «Sulle funzioni integrali», Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 40: 1021–1034