Επαναλαμβανόμενη συνάρτηση

Στα μαθηματικά, μια επαναλαμβανόμενη συνάρτηση είναι μια συνάρτηση που προκύπτει από την επανειλημμένη σύνθεση μίας συνάρτησης με τον εαυτό της ορισμένες φορές. Η διαδικασία εφαρμογής της ίδιας συνάρτησης πολλές φορές ονομάζεται επανάληψη.

Οι επαναλαμβανόμενες συναρτήσεις εμφανίζονται στην επιστήμη των υπολογιστών, στα δυναμικά συστήματα, στις ομάδες επανακανονικοποίησης και αποτελούν τη βάση των φράκταλ.

Ορισμός

Η επαναλαμβανόμενη, ακριβέστερα η δεύτερη επαναλαμβανόμενη, μιας συνάρτησης f, που ορίζεται σε ένα σύνολο X και έχει τιμές στο ίδιο αυτό σύνολο X, είναι η συνάρτηση $f\circ f,$ όπου $\circ$ σημειώνει τη σύνθεση συναρτήσεων. Με άλλα λόγια, για κάθε στοιχείο x του X

(f\circ f)(x)=f(f(x)).

Γενικότερα, με το n να είναι ένας θετικός ή μηδενικός ακέραιος αριθμός, η n-η επαναλαμβανόμενη $f^{n}$ μιας συνάρτησης f , που ορίζεται σε ένα σύνολο X και με τιμές στο ίδιο αυτό σύνολο X, ορίζεται με αναδρομή μέσω της σχέσης

f^{n}~{\stackrel {\mathrm {def} }{=}}~f\circ f^{n-1}.

Σύμφωνα με τη σύμβαση, για n = 0, $f^{0}~{\stackrel {\mathrm {def} }{=}}~\operatorname {id} _{X}$ , όπου $\operatorname {id} _{X}$ είναι η συνάρτηση ταυτότητας στο $X$ .

Ο συμβολισμός $f^{n}$ μπορεί να είναι διφορούμενος, καθώς χρησιμοποιείται όχι μόνο για την επανάληψη, αλλά και για την ύψωση σε δύναμη. Για το λόγο αυτό, ορισμένοι μαθηματικοί συμβολίζουν $f^{\circ n}$ την n-οστή επανάληψη μιας συνάρτησης $f$ .

Ακολουθίες επαναληπτικότητας

Οι ακόλουθες ταυτότητες ισχύουν για όλους τους θετικούς ή μηδενικούς ακεραίους $m$ και $n$ :

f^{m}\circ f^{n}=f^{n}\circ f^{m}=f^{m+n}~.

(f^{m})^{n}(x)=(f^{n})^{m}(x)=f^{mn}(x).

Για ένα στοιχείο $x$ του $X$ , η ακολουθία τιμών $f^{n}(x)$ είναι η τροχιά του $x$ .

Αν $x=f^{m}(x)$ για έναν μη μηδενικό ακέραιο $m$ , τότε $f^{n}(x)=f^{n+m}(x)$ (για κάθε $n$ ), η τροχιά λέγεται περιοδική και ο μικρότερος ακέραιος $m$ για ένα δεδομένο $x$ είναι η περίοδος της αντίστοιχης τροχιάς- το ίδιο το σημείο $x$ είναι ένα λεγόμενο περιοδικό σημείο. Στην επιστήμη των υπολογιστών, το πρόβλημα ανίχνευσης κύκλων είναι το αλγοριθμικό πρόβλημα που συνίσταται στην εύρεση του πρώτου περιοδικού σημείου μιας τροχιάς και της περιόδου της τροχιάς.

Σταθερά σημεία

Αν f(x) = x για ένα στοιχείο x του X (με άλλα λόγια, η περίοδος της τροχιάς του x είναι 1), τότε το x είναι ένα σταθερό σημείο της επαναληπτικής ακολουθίας. Το σύνολο των σταθερών σημείων συμβολίζεται με Fix(f). Διάφορα θεωρήματα εγγυώνται την ύπαρξη σταθερών σημείων σε ορισμένες περιπτώσεις, όπως το Θεώρημα σταθερού σημείου του Μπάναχ ή το Θεώρημα σταθερού σημείου του Μπρόουβερ.

Διάφορες τεχνικές μπορούν να χρησιμοποιηθούν για την επιτάχυνση της σύγκλισης των ακολουθιών που παράγονται με επαναλήψεις σταθερού σημείου.^[1]

Κατά τη διάρκεια της επαναληπτικότητας, μπορεί να υπάρχουν σύνολα που συστέλλονται και συγκλίνουν σε ένα μόνο σημείο: στην περίπτωση αυτή, το σημείο αυτό είναι ένα ελκυστικό σταθερό σημείο. Η επαναληπτικότητα μπορεί επίσης να δώσει την εμφάνιση σημείων που απομακρύνονται από ένα σταθερό σημείο, το οποίο τότε ονομάζεται ασταθές σταθερό σημείο^[2]. Άλλες οριακές συμπεριφορές είναι επίσης δυνατές. Όταν τα σημεία της τροχιάς συγκλίνουν σε ένα ή περισσότερα όρια, το σύνολο των συσσωρευμένων σημείων της τροχιάς ονομάζεται οριακό σύνολο ή ω-οριακό σύνολο.

Οι ιδέες της έλξης και της απώθησης γενικεύονται: τα σταθερά και τα ασταθή σύνολα μπορούν να κατηγοριοποιηθούν ανάλογα με τη συμπεριφορά των μικρών γειτονιών κατά την επανάληψη.

Αμετάβλητο μέτρο

Αν μας ενδιαφέρει η εξέλιξη μιας κατανομής πυκνότητας και όχι μιας διακριτής κατανομής ή ενός μεμονωμένου σημείου, η οριακή συμπεριφορά δίνεται από το αναλλοίωτο μέτρο. Μπορεί να απεικονιστεί ως η συμπεριφορά ενός νέφους σημείων ή σκόνης υπό μία επανάληψη. Το αναλλοίωτο μέτρο είναι ένα ιδιοδιάνυσμα του τελεστή Ρουέλ-Φρομπένιους-Περόν ή του τελεστή μεταφοράς, που αντιστοιχεί στην ιδιοτιμή 1. Μικρότερες ιδιοτιμές αντιστοιχούν σε ασταθείς, συρρικνούμενες καταστάσεις.

Σε γενικές γραμμές, εφόσον η επαναληπτικότητα αντιστοιχεί σε μετατόπιση, τόσο ο τελεστής μεταφοράς όσο και ο συγγενής του, ο τελεστής του Κούπμαν, μπορούν να ερμηνευθούν ως η δράση ενός τελεστή μετατόπισης σε ένα συμβολικό δυναμικό σύστημα. Η θεωρία των συμβολικών δυναμικών συστημάτων παρέχει ένα πλαίσιο για την κατανόηση πολλών επαναλαμβανόμενων συναρτήσεων, ιδίως εκείνων που οδηγούν σε χάος.

Κλασματική και αρνητική επανάληψη

Υπό ορισμένες προϋποθέσεις, είναι δυνατόν να οριστεί μια κλασματική επαναληπτικότητα μιας συνάρτησης. Για παράδειγμα, η μισή επανάληψη μιας συνάρτησης $f$ είναι μια συνάρτηση $g$ τέτοια ώστε $g(g(x))=f(x)$ . Αυτή η συνάρτηση $g$ μπορεί να γραφτεί με εκθετικό συμβολισμό < $f^{\frac {1}{2}}(x)$ . Παρομοίως, $f^{\frac {1}{3}}(x)$ είναι η συνάρτηση τέτοια ώστε $f^{\frac {1}{3}}(f^{\frac {1}{3}}(f^{\frac {1}{3}}(x)))=f(x)$ , και $f^{\frac {2}{3}}(x)$ μπορεί να οριστεί ως $f^{\frac {1}{3}}(f^{\frac {1}{3}}(x))$ , και ούτω καθεξής, με βάση την αρχή ότι $f^{m}\circ f^{n}=f^{n}\circ f^{m}=f^{m+n}~.$ . Η ιδέα μπορεί να γενικευτεί στην περίπτωση όπου ο αριθμός των επαναλήψεων $n$ γίνεται μια συνεχής παράμετρος- το σύστημα είναι τότε μια ροή που συνδέεται με μια εξίσωση Σρέντερ.

Οι αρνητικές επαναλήψεις αντιστοιχούν σε αντίστροφες διενέξεις συναρτήσεων και των συνθέσεών τους. Παραδείγματος χάριν, $f^{-1}(x)$ είναι το συνηθισμένο αντίστροφο της συνάρτησης $f$ , $f^{-2}(x)$ είναι το αντίστροφο που συντίθεται με τον εαυτό του, κ.λπ. Οι αρνητικές κλασματικές επαναλήψεις ορίζονται με παρόμοιο τρόπο με τις θετικές κλασματικές επαναλήψεις. Συγκεκριμένα, $f^{-{\frac {1}{2}}}(x)$ ορίζεται έτσι ώστε $f^{-{\frac {1}{2}}}(f^{-{\frac {1}{2}}}(x))=f^{-1}(x)$ .

Τύποι για κλασματική επαναληπτικότητα

Υπάρχουν διάφορες μέθοδοι για τον προσδιορισμό της κλασματικής επαναληπτικότητας. Η παρακάτω βασίζεται στη χρήση ενός σταθερού σημείου.

Καθορίζουμε ένα σταθερό σημείο a της συνάρτησης, με άλλα λόγια ένα σημείο a τέτοιο ώστε $f(a)=a$ .
Σταθερό σημείο $f^{n}(a)=a$ , για κάθε n που ανήκει στους πραγματικούς. Αυτό αντιστοιχεί στην πιο φυσική πρόσθετη συνθήκη που μπορεί να επιβληθεί στις επαναλήψεις.
Γράφουμε το $f^{n}(x)$ στη γειτονιά του σταθερού σημείου a ως σειρά Τέιλορ :
$f^{n}(x)=f^{n}(a)+(x-a){\frac {d}{dx}}f^{n}(x)|_{x=a}+{\frac {(x-a)^{2}}{2}}{\frac {d^{2}}{dx^{2}}}f^{n}(x)|_{x=a}+\cdots$
Αναπτύσσουμε :
$f^{n}\left(x\right)=f^{n}(a)+(x-a)f'(a)f'(f(a))f'(f^{2}(a))\cdots f'(f^{n-1}(a))+\cdots$
Χρησιμοποιώντας τη συνθήκη που τέθηκε στο βήμα 2 $f^{k}(a)=a$ , για όλα τα k, έχουμε:
$f^{n}\left(x\right)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1})\left(1+f'(a)+\cdots +f'(a)^{n-1}\right)+\cdots$
Απλοποιούμε χρησιμοποιώντας τη γεωμετρική πρόοδο :
$f^{n}\left(x\right)=a+(x-a)f'(a)^{n}+{\frac {(x-a)^{2}}{2}}(f''(a)f'(a)^{n-1}){\frac {f'(a)^{n}-1}{f'(a)-1}}+\cdots$
Μια ειδική περίπτωση είναι όταν $f'(a)=1$ - σε αυτή την περίπτωση :
$f^{n}\left(x\right)=x+{\frac {(x-a)^{2}}{2}}(nf''(a))+{\frac {(x-a)^{3}}{6}}\left({\frac {3}{2}}n(n-1)f''(a)^{2}+nf'''(a)\right)+\cdots$
Αν το n δεν είναι ακέραιος αριθμός, χρησιμοποιούμε τον τύπο $y^{n}=\exp(n\ln(y))$ .

Η διαδικασία αυτή μπορεί να συνεχιστεί επ' αόριστον, αλλά γενικά δεν είναι αποτελεσματική, καθώς οι όροι γίνονται όλο και πιο περίπλοκοι.

Παράδειγμα 1

Η συνάρτηση f ορίζεται από τη σχέση $f (x) = Cx + D$ με C ≠ 1, έχει σταθερό σημείο $a = D /(1- C)$ .

Η διαδικασία που αναλύσαμε παραπάνω δίνει :

f^{n}(x)={\frac {D}{1-C}}+(x-{\frac {D}{1-C}})C^{n}=C^{n}x+{\frac {1-C^{n}}{1-C}}D.

Παράδειγμα 2

Έστω ότι θέλουμε να υπολογίσουμε την τιμή ${\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}$ , για n επαναλήψεις. Εδώ η συνάρτηση ορίζεται από $f (x)= \sqrt 2 x$ . Ένα σταθερό σημείο είναι $a=f(2)=2$ .

Αναπτύσσοντας $f n (x)$ όπως εξηγήθηκε παραπάνω στη γειτονιά του 2, και θέτοντας x=1, έχουμε,

{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdots }}}=f^{n}(1)=2-(\ln 2)^{n}+{\frac {(\ln 2)^{n+1}((\ln 2)^{n}-1)}{4(\ln 2-1)}}\cdots .

Για n θετικό ακέραιο, οι τρεις πρώτοι όροι δίνουν το σωστό πρώτο δεκαδικό ψηφίο: $f n (1) = n \sqrt 2$ .

(Σημειώστε ότι αν χρησιμοποιήσουμε το άλλο σταθερό σημείο $a = f (4) = 4$ , αντί για το σταθερό σημείο 2, η σειρά αποκλίνει).

Για $n = -1$ η σειρά υπολογίζει την αντίστροφη συνάρτηση, $2\ln x/\ln 2$ .

Παράδειγμα 3

Αναπτύσσοντας στην περιοχή του σταθερού σημείου 1 τη συνάρτηση $f (x) = x b$ , προκύπτει η σειρά

f^{n}(x)=1+b^{n}(x-1)+{\frac {1}{2}}b^{n}(b^{n}-1)(x-1)^{2}+{\frac {1}{3!}}b^{n}(b^{n}-1)(b^{n}-2)(x-1)^{3}+\cdots ,

η οποία είναι απλά η σειρά Τέιλορ της x^(bⁿ) γύρω από το 1.

Τοπολογική συζυγία

Αν $f$ και $g$ είναι δύο επαναλαμβανόμενες συναρτήσεις, και αν υπάρχει ένας ομοιομορφισμός $h$ τέτοιος ώστε $g=h^{-1}\circ f\circ h$ , λέμε ότι $f$ και $g$ } είναι τοπολογικά συζυγείς.

Η επαναληπτικότητα διατηρεί την τοπολογική σύζευξη: πράγματι, $g^{n}=h^{-1}\circ f^{n}\circ h$ . Έτσι, αν ξέρουμε πώς να προσδιορίσουμε ένα σύστημα επαναληπτικών συναρτήσεων, ξέρουμε επίσης πώς να προσδιορίσουμε όλα τα τοπολογικά συζυγή συστήματα.

Παραδείγματος χάριν, η τριγωνική συνάρτηση είναι τοπολογικά συζυγής με τη λογιστική ακολουθία. Μια ειδική περίπτωση είναι η $f (x) = x +1$ η οποία δίνει ως επανάληψη της $g(x)=h^{-1}(h(x)+1)$

g^{n}(x)=h^{-1}(h(x)+n),

για οποιαδήποτε συνάρτηση $h$ .

Κάνοντας την αντικατάσταση $x=h^{-1}(y)=\phi (y)$ , προκύπτει

g(\phi (y))=\phi (y+1)

, με άλλα λόγια την εξίσωση του Άμπελ.

Στην απουσία ενός πραγματικού συνολικού ομοιομορφισμού, είναι συχνά δυνατή η επίλυση^[3] της εξίσωσης Σρέντερστην περιοχή ενός σταθερού σημείου για μια $Ψ$ συνάρτηση. Παραδείγματος χάριν, εάν $x$ = 0, $f$ (0) = 0, $f (x)$ είναι τοπικά συζυγής με μια διαστολή, $g (x) = f'(0) x$ , με άλλα λόγια

f(x)=\psi ^{-1}(f(0)\psi (x)).

Η τροχιά της επανάληψης, ή float, υπό κατάλληλες συνθήκες (π.χ. $f'(0) \neq 1$ ), γίνεται η συζυγής της τροχιάς του μονοωνύμου :

\psi ^{-1}(f'(0)^{n}\psi (x)),

όπου $n$ σε αυτή την έκφραση είναι ένας συνηθισμένος εκθέτης: με άλλα λόγια, η λειτουργική επανάληψη έχει μειωθεί σε έναν απλό πολλαπλασιασμό. Ο εκθέτης $n$ δεν μπορεί να είναι ούτε θετικός ούτε ακέραιος- τότε αντιστοιχεί σε ένα συνεχή χρόνο εξέλιξης για την τροχιά.^[4]

Το παράδειγμα 2 παραπάνω ισοδυναμεί, επομένως, με $f^{n}(x)=\psi ^{-1}((\ln 2)^{n}\psi (x))$ , για οποιοδήποτε n (όχι απαραίτητα ακέραιο), όπου $Ψ$ είναι η λύση της αντίστοιχης εξίσωσης Σρέντερ, $\psi ({\sqrt {2}}^{x})=\ln 2\psi (x)$ . Αυτή η λύση είναι επίσης το όριο, για m που τείνει στο άπειρο, της ${\frac {f^{m}(x)-2}{(\ln 2)^{m}}}$ .

Η μέθοδος αυτή είναι ισοδύναμη με τον αλγόριθμο που περιγράφεται στην προηγούμενη ενότητα, αλλά πιο ισχυρή και συστηματική στην πράξη.

Παραδείγματα

Για παραδείγματα επαναλαμβανόμενων συναρτήσεων, δείτε επίσης το σύνολο Μάντελμπροτ και τα Επαναλαμβανόμενα συστήματα συναρτήσεων.

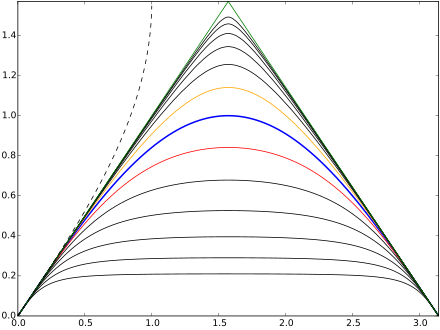
Ο Έρνστ Σρέντερ^[5] μελέτησε ειδικές περιπτώσεις της λογιστικής ακολουθίας το 1870:

(χαοτική περίπτωση) : $f(x)=4x(1-x)$ δίνει $\psi (x)=\arcsin ^{2}({\sqrt {x}})$ , ως εκ τούτου $f^{n}(x)=\sin ^{2}(2^{n}\arcsin({\sqrt {x}}))$ .
(μη χαοτική περίπτωση) : $f(x)=2x(1-x)$ δίνει $\psi (x)=-{\frac {1}{2}}\ln(1-2x)$ , και επομένως $f^{n}(x)=-{\frac {1}{2}}((1-2x)^{2^{n}}-1)$ .

Επαναλαμβανόμενες συναρτήσεις με κλειστή έκφραση

Για τις περισσότερες συναρτήσεις, δεν υπάρχει κλειστή έκφραση για την επαναλαμβανόμενη επανάληψη n^e. Ο παρακάτω πίνακας παραθέτει ορισμένες συναρτήσεις^[5] για τις οποίες υπάρχει τέτοια έκφραση. Όλες αυτές οι εκφράσεις ισχύουν για n, αρνητικούς ή κλασματικούς, καθώς και για θετικούς ακέραιους αριθμούς.

$f(x)$	$f^{n}(x)$
$x+b$	$x+nb$
$ax+b\ (a\neq 1)$	$a^{n}x+{\frac {a^{n}-1}{a-1}}b$
$ax^{b}\ (b\neq 1)$	$a^{\frac {b^{n}-1}{b-1}}x^{b^{n}}$
$ax^{2}+bx+{\frac {b^{2}-2b}{4a}}$	${\frac {2\alpha ^{2^{n}}-b}{2a}}$ όπου: $\alpha ={\frac {2ax+b}{2}}$
$ax^{2}+bx+{\frac {b^{2}-2b-8}{4a}}$	${\frac {2\alpha ^{2^{n}}+2\alpha ^{-2^{n}}-b}{2a}}$ όπου: $\alpha ={\frac {2ax+b\pm {\sqrt {(2ax+b)^{2}-16}}}{4}}$
${\frac {ax+b}{cx+d}}$ κλασματικός γραμμικός μετασχηματισμός ^[6]	${\frac {a}{c}}+{\frac {bc-ad}{c}}\left[{\frac {(cx-a+\alpha )\alpha ^{n-1}-(cx-a+\beta )\beta ^{n-1}}{(cx-a+\alpha )\alpha ^{n}-(cx-a+\beta )\beta ^{n}}}\right]$ όπου: $\alpha ={\frac {a+d+{\sqrt {(a-d)^{2}+4bc}}}{2}}$ $\beta ={\frac {a+d-{\sqrt {(a-d)^{2}+4bc}}}{2}}$
$g^{-1}{\Big (}h{\bigl (}g(x){\bigr )}{\Big )}$	$g^{-1}{\Bigl (}h^{n}{\bigl (}g(x){\bigr )}{\Bigr )}$
$g^{-1}{\bigl (}g(x)+b{\bigr )}$ εξίσωση Άμπελ	$g^{-1}{\bigl (}g(x)+nb{\bigr )}$
${\sqrt {x^{2}+b}}$	${\sqrt {x^{2}+bn}}$
$g^{-1}{\Bigl (}a\ g(x)+b{\Bigr )}\ (a\neq 1\vee b=0)$	$g^{-1}{\Bigl (}a^{n}g(x)+{\frac {a^{n}-1}{a-1}}b{\Bigr )}$
${\sqrt {ax^{2}+b}}$	${\sqrt {a^{n}x^{2}+{\frac {a^{n}-1}{a-1}}b}}$
$T_{m}(x)=\cos(m\arccos x)$ (Πολυώνυμο Τσέμπισεφ για ακέραιο m)	$T_{mn}=\cos(m^{n}\arccos x)$

Σημείωση: $ax 2 + bx + c$ είναι οι μόνες περιπτώσεις που έχουν λύση κλειστής μορφής. Επιλέγοντας αντίστοιχα b = 2 = –a and b = 4 = –a, ανάγονται στις μη χαοτικές και χαοτικές περιπτώσεις που συζητήθηκαν παραπάνω.

Μερικά από αυτά τα παραδείγματα συνδέονται με απλές συζυγίες^[7]

Αλυσίδες Μαρκόφ

Εάν η συνάρτηση είναι γραμμική και μπορεί να περιγραφεί από έναν στοχαστικό πίνακα, δηλαδή έναν πίνακα όπου το άθροισμα των καταχωρήσεων σε μια γραμμή (ή στήλη) είναι πάντα ίσο με 1, τότε το σύστημα των επαναλήψεων ονομάζεται αλυσίδα Μαρκόφ.

Στην επιστήμη των υπολογιστών

Στην επιστήμη των υπολογιστών, οι επαναλαμβανόμενες συναρτήσεις εμφανίζονται ως ειδικές περιπτώσεις των αναδρομικών συναρτήσεων και χρησιμοποιούνται στον λογισμό λάμδα ή σε πιο εξειδικευμένα θέματα, όπως η Δηλωτική σημασιολογία των προγραμμάτων υπολογιστών.

Ορισμοί με βάση επαναλαμβανόμενες συναρτήσεις

Δύο σημαντικές συναρτήσεις, το άθροισμα και το αντίστοιχο γινόμενο, μπορούν να οριστούν με βάση επαναληπτικές συναρτήσεις. Το άθροισμα ορίζεται από τη σχέση :

\left\{b+1,\sum _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,x+g(i)\}\right)^{b-a+1}\{a,0\}

και το γινόμενο από :

\left\{b+1,\prod _{i=a}^{b}g(i)\right\}\equiv \left(\{i,x\}\rightarrow \{i+1,xg(i)\}\right)^{b-a+1}\{a,1\}.

Συναρτησιακή παράγωγος

Η συναρτησιακή παράγωγος μιας επαναλαμβανόμενης συνάρτησης δίνεται από τον εξής αναδρομικό τύπο

{\frac {\delta f^{N}(x)}{\delta f(y)}}=f'(f^{N-1}(x)){\frac {\delta f^{N-1}(x)}{\delta f(y)}}+\delta (f^{N-1}(x)-y).

Δείτε επίσης

Παραπομπές

↑ L. Carleson et T. D. W. Gamelin, Complex dynamics, Berlin/New York, Springer-Verlag, coll. « Universitext: Tracts in Mathematics », 1993, 174 p. (ISBN 0-387-97942-5).
↑ Vasile Istratescu, Fixed Point Theory, An Introduction, D. Reidel, 1981 (ISBN 90-277-1224-7)
↑ «FUNKCIALAJ EKVACIOJ». www.math.sci.kobe-u.ac.jp. Ανακτήθηκε στις 8 Νοεμβρίου 2023.
↑ Curtright, Thomas; Zachos, Cosmas (2009-11-17). «Evolution profiles and functional equations». Journal of Physics A: Mathematical and Theoretical 42 (48): 485208. doi:10.1088/1751-8113/42/48/485208. ISSN 1751-8113. https://iopscience.iop.org/article/10.1088/1751-8113/42/48/485208.
↑ ^5,0 ^5,1 Schröder, Ernst (1870-06-01). «Ueber iterirte Functionen» (στα γερμανικά). Mathematische Annalen 3 (2): 296–322. doi:10.1007/BF01443992. ISSN 1432-1807. https://doi.org/10.1007/BF01443992.
↑ Brand, Louis, "A sequence defined by a difference equation," American Mathematical Monthly 62, September 1955, 489–492. online
↑ Katsura, Shigetoshi; Fukuda, Wataru (1985-04-01). «Exactly solvable models showing chaotic behavior». Physica A: Statistical Mechanics and its Applications 130 (3): 597–605. doi:10.1016/0378-4371(85)90048-2. ISSN 0378-4371. https://www.sciencedirect.com/science/article/pii/0378437185900482.

[1] L. Carleson et T. D. W. Gamelin, Complex dynamics, Berlin/New York, Springer-Verlag, coll. « Universitext: Tracts in Mathematics », 1993, 174 p. (ISBN 0-387-97942-5).

[2] Vasile Istratescu, Fixed Point Theory, An Introduction, D. Reidel, 1981 (ISBN 90-277-1224-7)

[3] «FUNKCIALAJ EKVACIOJ». www.math.sci.kobe-u.ac.jp. Ανακτήθηκε στις 8 Νοεμβρίου 2023.

[4] Curtright, Thomas; Zachos, Cosmas (2009-11-17). «Evolution profiles and functional equations». Journal of Physics A: Mathematical and Theoretical 42 (48): 485208. doi:10.1088/1751-8113/42/48/485208. ISSN 1751-8113. https://iopscience.iop.org/article/10.1088/1751-8113/42/48/485208.

[:0-5] 5,0 ^5,1 Schröder, Ernst (1870-06-01). «Ueber iterirte Functionen» (στα γερμανικά). Mathematische Annalen 3 (2): 296–322. doi:10.1007/BF01443992. ISSN 1432-1807. https://doi.org/10.1007/BF01443992.

[6] Brand, Louis, "A sequence defined by a difference equation," American Mathematical Monthly 62, September 1955, 489–492. online

[7] Katsura, Shigetoshi; Fukuda, Wataru (1985-04-01). «Exactly solvable models showing chaotic behavior». Physica A: Statistical Mechanics and its Applications 130 (3): 597–605. doi:10.1016/0378-4371(85)90048-2. ISSN 0378-4371. https://www.sciencedirect.com/science/article/pii/0378437185900482.

[1]

[2]

[3]

[4]

[5]

[6]

[7]