Ρυθμός μεταβολής της επιτάχυνσης
Στη φυσική ο ρυθμός μεταβολής της επιτάχυνσης είναι η παράγωγος της επιτάχυνσης ως προς το χρόνο και συνεπώς η δεύτερη παράγωγος της ταχύτητας και η τρίτη παράγωγος της θέσης ως προς το χρόνο. Δεν υπάρχει κάποιος ιδιαίτερος όρος στα ελληνικά που να εκφράζει αυτήν την έννοια. Στην αγγλική βιβλιογραφία έχουν εισαχθεί οι αγγλικοί όροι jerk (κατά κύριο λόγο) και jolt, ενώ για τη δεύτερη παράγωγο της επιτάχυνσης κάποιοι χρησιμοποιούν τους αγγλικούς όρους jounce ή snap, για την τρίτη τον όρο crackle και την τέταρτη pop, οι οποίοι όμως είναι μάλλον αδόκιμοι προκειμένου να αποδώσουν κατάλληλα τη γενικότητα αυτής της έννοιας για κάθε δυνατή εφαρμογή και έχουν εισαχθεί λόγω της ανάγκης συντομίας. Οι αντίστοιχοι όροι στα ελληνικά μεταφράζονται ως τράνταγμα, τίναγμα κ.ο.κ., οι οποίοι αποδίδουν εν μέρει την αίσθηση της απότομης μεταβολής της επιτάχυνσης που παρουσιάζεται σε ορισμένα φυσικά φαινόμενα, με την έμφαση όμως στην απότομη φύση της μεταβολής. Η χρήση τους πάντως στην ελληνική βιβλιογραφία θα ήταν μάλλον άκομψη αν όχι αδόκιμη. Αντιθέτως, δόκιμοι όροι που μπορούν να χρησιμοποιηθούν για αυτές τις έννοιες, τουλάχιστον για τις δύο πρώτες παραγώγους, είναι η ταχύτητα της επιτάχυνσης και η επιτάχυνση της επιτάχυνσης (όπου εννοείται ότι η παραγώγιση λαμβάνει χώρα ως προς το χρόνο). Εννοείται βέβαια ότι πάντοτε μπορούν να χρησιμοποιηθούν οι όροι «πρώτη παράγωγος της επιτάχυνσης», «δεύτερη παράγωγος», κ.ο.κ. οι οποίοι είναι όχι μόνο δόκιμοι αλλά και απολύτως ακριβείς.
Ο ρυθμός μεταβολής της επιτάχυνσης είναι ένα διανυσματικό μέγεθος και δεν υπάρχει κάποια ξεχωριστή μονάδα μέτρησης που χρησιμοποιείται ως το μέτρο του. Από την ανάλυση των μεγεθών του, [μήκος/χρόνος3], η μονάδα μέτρησής του στο Διεθνές Σύστημα Μονάδων (Γαλ. Système international d'unités (SI)) είναι το m/s3 (ή m·s-3). Ως μονάδα μέτρησής του χρησιμοποιείται επίσης η τυπική βαρύτητα ανά δευτερόλεπτο g/s.
Εκφράσεις[Επεξεργασία | επεξεργασία κώδικα]
Ο ρυθμός μεταβολής της επιτάχυνσης μπορεί να εκφράζεται με έναν από τους ακόλουθους ισοδύναμους τρόπους:
όπου
- η επιτάχυνση,
- η ταχύτητα,
- η θέση,
- ο χρόνος.
Δεν υπάρχει καθολικώς αποδεκτός συμβολισμός για το ρυθμό μεταβολής της επιτάχυνσης, αλλά συνήθως χρησιμοποιείται το . Χρησιμοποιείται επίσης η σύμβαση του Νεύτωνα για τις χρονικές παραγώγους ().
Λόγω της ύπαρξης τρίτων παραγώγων, στα μαθηματικά οι διαφορικές εξισώσεις της μορφής
ονομάζονται εξισώσεις ρυθμού μεταβολής της επιτάχυνσης. Έχει αποδειχθεί ότι μία τέτοια εξίσωση, η οποία είναι ισοδύναμη με ένα σύστημα τριών συνήθων μη-γραμμικών διαφορικών εξισώσεων πρώτης τάξης, είναι κατά μία έννοια η ελάχιστη ρύθμιση για λύσεις που επιδεικνύουν χαοτική συμπεριφορά. Αυτό είναι που προκαλεί το μαθηματικό ενδιαφέρον στα συστήματα που εμφανίζουν ρυθμό μεταβολής της επιτάχυνσης.
Τα συστήματα που περιλαμβάνουν μία τέταρτη ή μεγαλύτερης τάξης παράγωγο της θέσης, ονομάζονται αντίστοιχα συστήματα ανώτερων παραγώγων της επιτάχυνσης (αγγλ. hyperjerk).
Φυσιολογικές επιδράσεις και ανθρώπινη αντίληψη[Επεξεργασία | επεξεργασία κώδικα]
Η χρήση του ρυθμού μεταβολής της επιτάχυνσης στα διάφορα πεδία μελέτης της κίνησης του ανθρωπίνου σώματος γίνεται κατά κύριο λόγο για την περιγραφή και την καταμέτρηση της «απαλότητας» ή της ομαλότητας της κίνησης. Η ομαλή κίνηση του ανθρωπίνου σώματος ή η παραμονή του σε κατάσταση ηρεμίας, είναι αποτέλεσμα της εξισορρόπησης των δυνάμεων που ασκούνται ταυτόχρονα από πολλούς ανταγωνιστικούς μύες οι οποίοι ελέγχονται σε νευρωνικές οδούς του εγκεφάλου (προκειμένου για την κατευθυνόμενη κίνηση) ή μερικές φορές κατά μήκος αντανακλαστικών τόξων. Για την εξισορρόπηση κάποιας δεδομένης δύναμης (π.χ. κατά το κράτημα ή το τράβηγμα ενός βάρους) η μετακεντρική έλικα δημιουργεί ένα κύκλωμα ελέγχου για την επίτευξη αυτής της ισορροπίας, ρυθμίζοντας την ένταση των μυών σύμφωνα με τη θέση που ανιχνεύει ο ενεργοποιητής. Αν το φορτίο αλλάζει πιο γρήγορα από την κατάλληλη προσαρμοστική απόκριση που παρέχει το κύκλωμα ελέγχου, η ισορροπία δεν μπορεί να διατηρηθεί. Αυτό διότι οι τεντωμένοι μύες δεν μπορούν να χαλαρώσουν ή να συσταλούν αρκετά γρήγορα και να αλλάξουν κατεύθυνση, μέχρι ο νευρωνικός βρόχος ελέγχου να καταφέρει να ανακτήσει τον έλεγχο. Φυσικά, ο χρόνος αντίδρασης είναι περιορισμένος υπό φυσιολογικές συνθήκες και επίσης εξαρτάται από το επίπεδο προσοχής: μία αναμενόμενη αλλαγή θα σταθεροποιηθεί γρηγορότερα από μια ξαφνική πτώση ή αύξηση του φορτίου.
Οι επιβάτες στα μεταφορικά μέσα, οι οποίοι χρειάζονται αυτό το χρόνο για να προσαρμοστούν στις αλλαγές ταχύτητας του μέσου και να ρυθμίσουν την ένταση των μυών τους (αλλιώς ενδέχεται να υποστούν π.χ. αυχενικούς τραυματισμούς) ώστε να μπορούν με ασφάλεια να υποστούν μία μικρότερη από τη μέγιστη επιτάχυνση και άρα μικρότερο τράνταγμα,[1] ώστε να αποφευχθεί η απώλεια ελέγχου που θα έθετε σε κίνδυνο τη σωματική τους ακεραιότητα. Ακόμη και όταν η επιβατική ασφάλεια δεν είναι ζήτημα, το υπερβολικό τράνταγμα μπορεί να οδηγήσει σε μια δυσάρεστη μετατόπιση σε ένα ανελκυστήρα, τραμ κλπ. έτσι οι μηχανικοί έχουν κάνει σημαντική προσπάθεια στο σχεδιασμό ώστε να ελαχιστοποιηθεί η πιθανότητα σπασμωδικής κίνησης.
Δεδομένου ότι οι δυνάμεις αλλάζουν χρονικά κατά ένα κατάλληλο ποσοστό (δηλαδή, κατάλληλο τράνταγμα) είναι η αιτία δονήσεων και οι δονήσεις επηρεάζουν σημαντικά την ποιότητα της μεταφοράς, συνεπώς υφίσταται πολύ καλός λόγος για να ελαχιστοποιηθεί το τράνταγμα στα μέσα μεταφοράς.
Ως ένα καθημερινό παράδειγμα, η οδήγηση σε ένα αυτοκίνητο μπορεί να καταδείξει τα αποτελέσματα της επιτάχυνσης και του ρυθμού μεταβολής της επιτάχυνσης. Οι πιο έμπειροι οδηγοί επιταχύνουν ομαλά, αλλά οι αρχάριοι οδηγούν σπασμωδικά.
- Η αλλαγή ταχυτήτων με το συμπλέκτη είναι ένα γνωστό παράδειγμα: αν και η επιτάχυνση οριοθετείται από την ισχύ του κινητήρα, ένας άπειρος οδηγός σας μπορεί να προκαλέσει ένα αισθητό τράνταγμα κατά την αλλαγή, εξαιτίας της απότομης δύναμης που ασκείται κατά τη σύμπλεξη στον κινητήρα.
- Τα αγωνιστικά αυτοκίνητα υψηλής ισχύος προσφέρουν ούτως ή άλλως στον οδηγό την αίσθηση της πίεσης στο κάθισμα κατά την επιτάχυνση. Κατά τις πρώτες στιγμές της επιτάχυνσης όμως, όταν η ροπή του κινητήρα αυξάνεται με την ταχύτητα περιστροφής, η επιτάχυνση αυξάνεται ραγδαία και π.χ. ένα μικρό αυχενικό τράνταγμα μπορεί να γίνει αισθητό - αν και, ως επί το πλείστον, μπορεί να καλύπτεται από το τράνταγμα της αλλαγής ταχύτητας.
- Κατά το ξεκίνημα της πέδησης (σε περίπτωση έκτακτης ανάγκης), το σώμα ενός επιβάτη τινάζεται μπροστά πιο απότομα από ότι θεωρητικά θα συνέβαινε ως αποτέλεσμα επιβράδυνσης με σταθερή τιμή. Σε μία σύγκρουση αυτό το φαινόμενο είναι αισθητό σε ακόμα μεγαλύτερο βαθμό. Καθώς οι δοκιμές σύγκρουσης σε ανθρώπους ή ζώα δημιουργούν ηθικά ζητήματα, χρησιμοποιούνται ανδρείκελα (ή σπανίως πτώματα), τα οποία όμως, δεν παρουσιάζουν τις φυσιολογικές αντιδράσεις στο τράνταγμα που προκαλούνται από τον ενεργό βρόχο ελέγχου του εγκεφάλου.
- Ένα εύκολα αναπαραγώγιμο πείραμα για να επιδειχτεί το τράνταγμα, είναι το εξής: Ο οδηγός επιβραδύνει ένα όχημα που κινείται με μέτρια ταχύτητα με δύο διαφορετικούς τρόπους:
- Ο οδηγός ασκεί μέτρια αλλά σταθερή δύναμη στο μοχλό πέδησης μέχρι το όχημα να έρθει σε στάση και παύει να ασκεί δύναμη τη στιγμή ακριβώς που το όχημα έρχεται σε στάση.
- Ο οδηγός ασκεί μέτρια αλλά σταθερή δύναμη στο μοχλό πέδησης αλλά, λίγο πριν το όχημα έλθει σε στάση, μειώνει προοδευτικά τη δύναμη που ασκεί μέχρι τη στιγμή ακριβώς προτού το όχημα έλθει σε στάση οπότε απελευθερώνει πλήρως το μοχλό πέδησης.
Ο λόγος για το πολύ πιο αισθητό τράνταγμα με τον πρώτο τρόπο πέδησης είναι η ασυνέχεια της επιβράδυνσης, η οποία αρχικά έχει μία σταθερή τιμή λόγω της σταθερής δύναμης που ασκείται στο μοχλό πέδησης αλλά μηδενίζεται απότομα όταν οι τροχοί σταματήσουν να περιστρέφονται. Σημειωτέον ότι θα είναι μηδενικός ο ρυθμός μεταβολής της επιτάχυνσης αν το όχημα συνεχίσει να κινείται, αλλά αντίθετα, με την ίδια επιτάχυνση. Αυτό συμβαίνει όταν ένα όχημα που κινείται ανοδικά σε ανηφορικό οδόστρωμα με μικρή σταθερή ταχύτητα επιβραδύνεται μόνο ως αποτέλεσμα της δύναμης της βαρύτητας. Ένας έμπειρος οδηγός γνωρίζει πώς να ξεκινήσει και να σταματήσει την πέδηση δίχως να προκαλέσει τράνταγμα.
Παράγωγοι του χρόνου και δυνάμεις[Επεξεργασία | επεξεργασία κώδικα]
Θέση , η μηδενική παράγωγος[Επεξεργασία | επεξεργασία κώδικα]
Η πιο γνωστή δύναμη που σχετίζεται με τη θέση ενός σώματος, συσχετίζεται μέσω του νόμου του Χουκ (αγγλ. Hooke) με τη δυσκαμψία (δυστένεια) ενός ελατηρίου:
Αυτή είναι μια δύναμη που αντιτίθεται στην αύξηση της μετατόπισης.
Ταχύτητα , η πρώτη παράγωγος[Επεξεργασία | επεξεργασία κώδικα]
Ένα σωματίδιο που κινείται σε ένα ιξώδες υγρό δέχεται μία αντίσταση η οποία ανάλογα με τον αριθμό Ρέυνολντς (αγγλ. Reynolds) και την επιφάνειά του, κυμαίνεται από το να είναι ανάλογη με την ταχύτητα, , έως το τετράγωνο της ταχύτητας, , σύμφωνα με την εξίσωση:
όπου
- η επιτάχυνση,
- η ταχύτητα,
- η θέση,
- ο χρόνος
Ο συντελεστής τριβής εξαρτάται από το σχήμα του αντικειμένου και τον αριθμό Ρέυνολντς, που με τη σειρά του οποία εξαρτάται από την ταχύτητα.
Επιτάχυνση , η δεύτερη παράγωγος[Επεξεργασία | επεξεργασία κώδικα]
Η επιτάχυνση, , είναι σύμφωνα με το δεύτερο νόμο του Νεύτωνα
δεσμευμένη με μία δύναμη ανάλογη με τη μάζα .
Ανώτερες παράγωγοι[Επεξεργασία | επεξεργασία κώδικα]
Στην κλασική μηχανική των στερεών σωμάτων δεν υπάρχουν δυνάμεις, που να συνδέονται με τις ανώτερες παραγώγους της επιτάχυνσης. Ωστόσο, όχι μόνο οι φυσιολογικές επιδράσεις του ρυθμού μεταβολής της επιτάχυνσης, αλλά και οι ταλαντώσεις και οι διαδόσεις παραμορφώσεων σε μη-ιδανικά στερεά σώματα, απαιτούν διάφορες τεχνικές για τον έλεγχο της κίνησης ώστε να αποφευχθούν οι ενδεχόμενες καταστροφικές δυνάμεις, που μπορεί να προκύψουν. Η ΝΑΣΑ (Αγγλ. NASA) στο σχεδιασμό του Διαστημικού Τηλεσκοπίου Χαμπλ (Αγγλ. Hubble) δεν περιόρισε μόνο το ρυθμό μεταβολής της επιτάχυνσης στις προδιαγραφές του, αλλά και την αμέσως επόμενη ανώτερη παράγωγο, τη δεύτερη παράγωγο της επιτάχυνσης.
Για μια δύναμη ανάκρουσης η οποία ασκείται σε επιταχυνόμενα φορτισμένα σωματίδια, που εκπέμπουν ακτινοβολία, η οποία είναι ανάλογη με το ρυθμό μεταβολής της επιτάχυνσης και το τετράγωνο του φορτίου, δείτε σχετικά τη δύναμη Άμπραχαμ–Λόρεντζ (αγγλ. Abraham–Lorentz). Μια πιο προηγμένη θεωρία, που εφαρμόζεται στη σχετικιστική και κβαντική θεώρηση, λαμβάνοντας υπόψη την αυτο-ενέργεια, παρέχεται στη θεωρία απορρόφησης Γουήλερ-Φάινμαν (αγγλ. Wheeler–Feynman).
Σε ένα εξιδανικευμένο περιβάλλον[Επεξεργασία | επεξεργασία κώδικα]
Υπό πραγματικές συνθήκες, εξαιτίας της ύπαρξης μηχανικών παραμορφώσεων, της διακριτότητας (τουλάχιστον σε φαινόμενα που λαμβάνουν χώρα στο επίπεδο της κλίμακας Πλανκ (Αγγλ. Planck), δηλαδή κβαντικά φαινόμενα) και άλλων αιτιών, ασυνέχειες στην επιτάχυνση δεν παρατηρούνται. Παρ' όλα αυτά, για τις τυπικές ιδανικές συνθήκες που θεωρούνται ως δεδομένες στα πλαίσια της κλασικής μηχανικής (άκαμπτα σώματα, ομαλές τροχιές κίνησης, απουσία τριβών, κλπ.) για μία ιδανική σημειακή μάζα κινούμενη κατά μήκος μίας τμηματικά ομαλής, συνεχούς τροχιάς, η εμφάνιση ασυνεχειών τύπου άλματος στην επιτάχυνση στα σημεία όπου η τροχιά δεν είναι ομαλή και αντίστοιχα ο άπειρος ρυθμός μεταβολής της επιτάχυνσης σε αυτά τα σημεία, είναι άμεση λογική συνέπεια (δείτε δύο παραδείγματα παρακάτω). Με βάση όμως τα δεδομένα της κίνησης υπό εξιδανικευμένες συνθήκες, η σημασία του ρυθμού μεταβολής της επιτάχυνσης υπό πραγματικές καταστάσεις μπορεί να περιγραφεί ποιοτικά, να εξηγηθεί και να προβλεφθεί.
Η ασυνέχεια τύπου άλματος στην επιτάχυνση μπορεί να αναπαρασταθεί υιοθετώντας για την περιγραφή του ρυθμού μεταβολής της επιτάχυνσης μία συνάρτηση δέλτα πολλαπλασιασμένη επί το ύψος αυτού του άλματος (η ολοκλήρωση μίας συνάρτησης δέλτα δίνει μία συνάρτηση βήματος που μπορεί να χρησιμοποιηθεί για την αναπαράσταση μίας ασυνέχειας τύπου άλματος).
Ας θεωρήρουμε μία συνεχή, τμηματικά ομαλή τροχιά, η οποία σχηματίζεται από ένα κυκλικό τόξο, ακτίνας , και ένα ευθύγραμμο τμήμα αρχόμενο από τη μία άκρη του τόξου με κλίση ίδια με αυτή του τόξου στην άκρη αυτή κατασκευασμένη με τέτοιο τρόπο ώστε ένα κινούμενο σημειακό σώμα που διαγράφει την τροχιά αυτήν να μην αναστρέφει σε κανένα σημείο την πορεία του. Ας θεωρήρουμε τώρα ότι η συνιστώσα της επιτάχυνσης του σώματος αυτού, που είναι εφαπτομενικά κείμενη ως προς την τροχιά αυτή, είναι μηδενική. Τότε, η κάθετη, ως προς την κλίση της τροχιάς, συνιστώσα της επιτάχυνσης του σώματος είναι μηδενική κατά μήκος του ευθύγραμμου τμήματος αλλά έχει τιμή επί του κυκλικού τόξου (γωνιακή ή κεντρομόλος επιτάχυνση). Συνεπώς, η τιμή της επιτάχυνσης εμφανίζει μία ασυνέχεια τύπου άλματος στο σημείο σύνδεσης του κυκλικού τόξου και του ευθύγραμμου τμήματος και, επομένως, η τιμή του ρυθμού μεταβολής της επιτάχυνσης περιγράφεται από τη συνάρτηση δέλτα πολλαπλασιασμένη με την τιμή της γωνιακής επιτάχυνσης. Η ασυνέχεια αυτή, θα μπορούσε να ειπωθεί ότι, οφείλεται, κατά κύριο λόγο, στις γεωμετρικές ιδιότητες της τροχιάς (αλλά βέβαια και στο γεγονός ότι το σώμα συνεχίζει να κινείται και δεν σταματάει στο σημείο που ενώνονται τα δύο τμήματα της τροχιάς). Δείτε παρακάτω για μια πιο συγκεκριμένη εφαρμογή.
Αν θεωρήσουμε ένα εξιδανικευμένο ελατήριο και επίσης εξιδανικευμένη δύναμη τριβής, ανάλογη με την κάθετη αντίδραση και αντίθετες στην ταχύτητα, υπάρχει άλλο ένα παράδειγμα ασυνεχούς επιτάχυνσης. Επίσης συνδέεται μία μάζα στο ελατήριο και ταλαντώνονται σε μια επίπεδη, ιδεατή επιφάνεια με τριβή. Κάθε φορά που η ταχύτητα αλλάζει πρόσημο (στα μέγιστα των μετατοπίσεων), το μέγεθος της δύναμης πάνω στη μάζα, το οποίο είναι το διανυσματικό άθροισμα της δύναμης ελατηρίου και της δύναμης τριβής, αλλάζει κατά δύο φορές το μέγεθος της δύναμης τριβής, εφόσον η δύναμη του ελατηρίου είναι συνεχής και η δύναμη τριβής αντιστρέφει την κατεύθυνσή της, όταν αντιστρέφεται η ταχύτητα. Επομένως, η επιτάχυνση κάνει άλμα κατά αυτή την ποσότητα διαιρεμένη με τη μάζα. Δηλαδή, η μάζα υπόκειται σε ασυνεχή επιτάχυνση και ο ρυθμός μεταβολής της επιτάχυνσης περιέχει δέλτα του Dirac, κάθε φορά που η μάζα περνάει από τις (μειούμενες) μέγιστες μετατοπίσεις μέχρι να σταματήσει, επειδή η στατική δύναμη τριβής προσαρμόζεται στην εναπομένουσα δύναμη ελατηρίου, για τη διατήρηση ισορροπίας με μηδενική συνισταμένη δύναμη και μηδενική ταχύτητα.
Το παράδειγμα με το αυτοκίνητο εξαρτάται από τον τρόπο που τα φρένα λειτουργούν σε ένα περιστρεφόμενο τύμπανο ή σε ένα δίσκο. Όσο ο δίσκος περιστρέφεται τα μαξιλάρια φρένων (τακάκια) ενεργούν για να επιβραδύνουν το όχημα μέσω των κινητικών δυνάμεων τριβής που δημιουργούν μια σταθερή ροπή πεδήσεως στο δίσκο. Αυτό μειώνει την περιστροφή γραμμικά με σταθερή γωνιακή επιτάχυνση μέχρι να μηδενιστεί, αλλά όταν η περιστροφή φτάνει ακριβώς μηδέν, η μέχρι πρότινος σταθερή δύναμη τριβής ξαφνικά πέφτει στο μηδέν, όπως και η ροπή και η αντίστοιχη επιτάχυνση του αυτοκινήτου. Αυτό βέβαια, αγνοεί όλα τις επιδράσεις ολίσθησης των ροδών, τη βύθιση της ανάρτησης, την πραγματική παραμόρφωση όλων των ιδανικά άκαμπτων μηχανισμών, κλπ. Μια ξαφνική πτώση στην επιτάχυνση αντιστοιχεί σε δέλτα του Dirac στο φυσικό ρυθμό μεταβολής της επιτάχυνσης, το οποίο όμως εξομαλύνεται από το πραγματικό περιβάλλον. Οι αθροιστικές επιδράσεις του τελευταίου στο φυσιολογικά αντιληπτό ρυθμό μεταβολής της επιτάχυνσης, είναι ανάλογες με την απόσβεση.
Ένα άλλο παράδειγμα σημαντικού ρυθμού μεταβολής της επιτάχυνσης, ανάλογου με την πρώτη ρύθμιση, δίνεται κόβοντας το σκοινί στο ενώ ένα υλικό σημείο περιστρέφεται γύρω από ένα κέντρο. Όταν το σχοινί κόβεται, η κυκλική διαδρομή με μη μηδενική κεντρομόλο επιτάχυνση αλλάζει απότομα σε μια ευθεία πορεία, με ξαφνικά χωρίς δύναμη προς την κατεύθυνση του πρώην κέντρου. Φανταστείτε μία μονομοριακή ίνα που κόβεται από λέιζερ και φτάνετε σε πολύ υψηλά ποσοστά ρυθμού μεταβολής της επιτάχυνσης, λόγω του εξαιρετικά σύντομου χρόνου κοπής.
Στην περιστροφή[Επεξεργασία | επεξεργασία κώδικα]

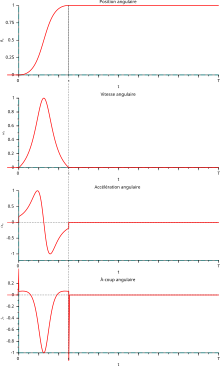
Σκεφτείτε την περιστροφική κίνηση ενός στερεού σώματος γύρω από ένα σταθερό άξονα σε ένα αδρανειακό σύστημα αναφοράς. Ο προσανατολισμός του στερεού μπορεί να εκφραστεί από μια γωνία η γωνιακή θέση, από την οποία μπορεί κανείς να εκφράσει:
- η γωνιακή ταχύτητα ως η χρονική παράγωγος της
- η γωνιακή επιτάχυνση ως η χρονική παράγωγος της .
Παραγωγίζοντας την ως προς το χρόνο, προσδιορίζεται o ρυθμός μεταβολής της γωνιακής επιτάχυνσης:
Η γωνιακή επιτάχυνση αντιστοιχεί στο ποσοστό της ροπής που δρα στο σώμα και στη ροπή αδράνειας του σώματος ως προς το στιγμιαίο άξονα περιστροφής. Μια ξαφνική αλλαγή στη ροπή αυξάνει σημαντικά το ρυθμό μεταβολής της γωνιακής επιτάχυνσης.
Στη γενική περίπτωση ενός στερεού σώματος που κινείται στο χώρο μπορεί να μοντελοποιηθεί από έναν κινητικό κοχλία, που καθορίζει σε κάθε στιγμή ένα (αξονικό) διάνυσμα, τη γωνιακή ταχύτητα και ένα (πολικό) διάνυσμα, τη γραμμική ταχύτητα . Από αυτά η γωνιακή επιτάχυνση ορίζεται ως
και συνεπώς το ρυθμό μεταβολής της γωνιακής επιτάχυνσης
Σκεφτείτε για παράδειγμα ένα δίσκο Geneva, ένα μηχανισμό για τη δημιουργία διακοπτόμενης περιστροφής ενός οδηγούμενου τροχού (μπλε) από τη συνεχή περιστροφή άλλου οδηγού τροχού (κόκκινο). Σε έναν κύκλο του οδηγού τροχού, υπάρχει μια μεταβολή στη γωνιακή θέση θ του οδηγούμενου τροχού κατά ένα τέταρτο του κύκλου και μια σταθερή γωνιακή θέση στο υπόλοιπο του κύκλου.
Εξαιτίας του αναγκαίου πεπερασμένου πάχους της υποδοχής για την προεξοχή του οδηγού, αυτή η συσκευή εμφανίζει μία ασυνέχεια στη γωνιακή επιτάχυνση α και επομένως, ένα θεωρητικά άπειρο (πρακτικά πολύ υψηλό) ρυθμό μεταβολής της γωνιακής επιτάχυνσης ζ στον οδηγούμενο τροχό.
Αυτό δεν αποκλείει το μηχανισμό από το να χρησιμοποιείται, π.χ. σε προβολείς ταινίας για τη σταδιακή μεταφορά της ταινίας με αξιοπιστία (πολύ μεγάλη διάρκεια ζωής) και χαμηλό θόρυβο, δεδομένου ότι το φορτίο είναι πολύ μικρό. Συγκεκριμένα, το σύστημα οδηγεί μόνο αυτό το τμήμα της ταινίας που βρίσκεται εντός του διαδρόμου της προβολής, έτσι ώστε να επηρεάζεται μια πολύ μικρή μάζα (πλαστικό φιλμ μερικών εκατοστών πάχους), με χαμηλή τριβή και σε μέτρια ταχύτητα (2.4 m/s, 8.6 km/h).
Για να αποφευχθεί η εμφάνιση του ρυθμού μεταβολής της επιτάχυνσης που είναι εγγενής σε μια συσκευή μονού εκκεντροφόρου άξονα, μπορεί να χρησιμοποιηθεί μια αντίστοιχη διπλού εκκεντροφόρου που είναι πιο ογκώδης και πιο ακριβή, αλλά και πιο αθόρυβη. Αυτή λειτουργεί με δύο έκκεντρα, ένα σε συνεχή περιστροφή και ένα άλλο που μετακινείται για ένα κλάσμα της πλήρους περιστροφής. Οι φωτογραφίες δείχνουν μια βηματική διαδρομή κατά μία έκτη και μία τρίτη περιστροφή, αντίστοιχα, ανά πλήρη περιστροφή του οδηγού εκκεντροφόρου. Σημειώστε ότι δύο από τους βραχίονες του βηματικού τροχού είναι πάντα σε επαφή με το διπλό εκκεντροφόρο, έτσι δεν υπάρχει κανένα ακτινικό διάκενο. Για τη λεπτομερή λειτουργία συσκευών διπλού εκκεντροφόρου, δείτε τις μεγεθυμένες φωτογραφίες.
Γενικά, συνδυασμένες επαφές μπορούν να χρησιμοποιηθούν για να αποφεύγεται η εμφάνιση σημαντικού μεγέθους του ρυθμού μεταβολής της επιτάχυνσης (και επίσης η φθορά και ο θόρυβος) σχετικά με ένα ενιαίο "ακόλουθο", π.χ., γλιστρώντας κατά μήκος μιας υποδοχής και έτσι αλλάζοντας το σημείο επαφής από τη μία πλευρά της υποδοχής στην άλλη, χρησιμοποιώντας δύο "ακόλουθους" που πάντα γλιστρούν κατά μήκος το ίδιο, στη μία πλευρά ο καθένας.
Σε ελαστικά παραμορφώσιμο υλικό[Επεξεργασία | επεξεργασία κώδικα]
Δύναμη/επιτάχυνση που ενεργεί σε ελαστικά παραμορφώσιμη μάζα θα δημιουργήσει παραμόρφωση, η οποία εξαρτάται από τη δυσκαμψία και την επιτάχυνση που εφαρμόζεται. Αν η αλλαγή της δύναμης αυτής είναι αργή, ο ρυθμός μεταβολής της επιτάχυνσης είναι μικρός, και η διάδοση της παραμόρφωσης μέσα από το σώμα μπορεί να θεωρηθεί ακαριαία σε σύγκριση με την αλλαγή στην επιτάχυνση. Το παραμορφωμένο σώμα ενεργεί σαν να ήταν σε μια οιονεί-στατική κατάσταση. Αυτό είναι το κοινό στοιχείο που μόνο μια μεταβαλλόμενη δύναμη, δηλαδή με μη-μηδενικό ρυθμό μεταβολής της επιτάχυνσης, μπορεί να προκαλέσει μηχανικά (ή σε ένα φορτισμένο σωματίδιο: ηλεκτρομαγνητική) κύματα που εξαπλώνονται. Έτσι, για μη μηδενικό έως υψηλό ρυθμό μεταβολής της επιτάχυνσης, θεωρούμε ένα ωστικό κύμα και τη διάδοσή του μέσω του σώματος. Η αριστερή εικόνα δείχνει την διάδοση της παραμόρφωσης ως ένα συμπιεστικό, επίπεδο κύμα μέσα σε ένα ελαστικά παραμορφώσιμο υλικό. Για γωνιακό ρυθμό μεταβολής της επιτάχυνσης, τα κύματα παραμόρφωσης διαδίδονται κυκλικά και προκαλούν διατμητικές τάσεις, όπως φαίνεται στην εικόνα στα δεξιά, το οποίο μπορεί επίσης να διεγείρει άλλες μορφές δόνησης. Ως συνήθως με τα κύματα, πρέπει να εξεταστούν οι ανακλάσεις τους σε όλα τα όρια και τις μοτίβα συμβολής που προκύπτουν (είτε καταστρεπτική είτε ενισχυτική συμβολή), η οποία μπορεί να οδηγήσει σε υπέρβαση των ορίων δομικής ακεραιότητας. Ως μια πρόχειρη εκτίμηση, τα κύματα παραμόρφωσης οδηγούν σε δονήσεις ολόκληρης της συσκευής και γενικά, οι δονήσεις προκαλούν θόρυβο, φθορά και ειδικά σε περιπτώσεις συντονισμού, ακόμα και θραύση.

Η εικόνα στα αριστερά δείχνει μια συγκεντρωμένη μάζα στην κορυφή που κάμπτει τον ελαστικό ιστό με το οποίο είναι συνδεδεμένη, προς τα αριστερά, όταν το μπλοκ στη βάση επιταχύνεται προς τα δεξιά. Όταν το μπλοκ σταματά να επιταχύνει, η κορυφή του ιστού θα ξεκινήσει μία ταλάντωση (με απόσβεση) κάτω από την επίδραση της δυσκαμψίας του ιστού. Αυτό θα μπορούσε να εξηγήσει, πως ένας μεγαλύτερος (περιοδικός) ρυθμός μεταβολής της επιτάχυνσης μπορεί να διεγείρει ένα μεγαλύτερο εύρος ταλαντώσεων, επειδή οι όποιες μικρές ταλαντώσεις αποσβένονται πριν βγουν ενισχυμένες από άλλο ένα ωστικό κύμα.

Μπορεί κανείς να ισχυριστεί ότι μια πιο απότομη κλίση της επιτάχυνσης, δηλαδή μεγαλύτερο ρυθμό μεταβολής της επιτάχυνσης, διεγείρει ισχυρότερες συνιστώσες του ωστικού κύματος με υψηλότερες συχνότητες, που ανήκουν σε υψηλότερους συντελεστές Fourier, και έτσι μια αυξημένη πιθανότητα διέγερσης συντονισμού.
Ως γενικός κανόνας, για τη μείωση του εύρους των τασικών κυμάτων που προκαλούν δονήσεις, οποιαδήποτε κίνηση μαζών πρέπει να διαμορφώνεται με τον περιορισμό του ρυθμού μεταβολής της επιτάχυνσης, δηλαδή κρατώντας την επιτάχυνση συνεχή και τις κλίσεις της όσο το δυνατόν πιο επίπεδες. Δεδομένου ότι πλέον οι περιγραφόμενες επιδράσεις σχεδόν δεν επιδέχονται αφηρημένα μοντέλα, οι διάφοροι προτεινόμενοι αλγόριθμοι για τη μείωση των δονήσεων περιλαμβάνουν ακόμη υψηλότερες παραγώγους, όπως το jounce, ή προτείνουν συνεχή καθεστώς, όχι μόνο για την επιτάχυνση αλλά και για το ρυθμό μεταβολής της επιτάχυνσης. Μια ιδέα είναι π.χ. η διαμόρφωση ημιτονοειδούς επιτάχυνσης και επιβράδυνσης με μηδενική επιτάχυνση στο ενδιάμεσο (δείτε το προφίλ στα δεξιά), κάνοντας την ταχύτητα να δείχνει ημιτονοειδής με σταθερή μέγιστη ταχύτητα επίσης. Ο ρυθμός μεταβολής της επιτάχυνσης όμως θα παραμείνει ασυνεχές στα σημεία όπου η επιτάχυνση εισέρχεται και εξέρχεται από τις μηδενικές-φάσεις.
Στη χάραξη οδών και σιδηροδρόμων[Επεξεργασία | επεξεργασία κώδικα]

Στις περιπτώσεις αυτές, όπου η συνιστώσα της ταχύτητας που κείται εφαπτομενικά ως προς τη διαδρομή είναι σταθερή (οπότε και η αντίστοιχη συνιστώσα του ρυθμού μεταβολής της επιτάχυνσης είναι μηδενική), το ενδιαφέρον, κατά τη γεωμετρική σχεδίαση, εστιάζεται στην κεντρομόλο επιτάχυνση και στη συνιστώσα του ρυθμού μεταβολής της επιτάχυνσης που κείται κάθετα ως προς τη διεύθυνση της διαδρομής (κεντρομόλο συνιστώσα). Αυτό γίνεται διότι ο τελευταίος οφείλεται σε καθαρά γεωμετρικούς λόγους, καθώς οποιαδήποτε αλλαγή στην καμπυλότητα της διαδρομής έχει ως αποτέλεσμα ένα κινούμενο σώμα πάνω στη διαδρομή να εμφανίζει μία μη-μηδενική συνισταμένη του ρυθμού μεταβολής της επιτάχυνσής του στο επίπεδο που τέμνει κάθετα τη διεύθυνση της κίνησής του.
Για να αποφευχθεί ο υπερβολικά μεγάλος (κεντρομόλος) ρυθμός μεταβολής της επιτάχυνσης κατά τη μετάβαση π.χ. από ένα ευθύγραμμο σε ένα καμπύλο τμήμα της διαδρομής ή αντίστροφα (δηλαδή όπου γενικά εμφανίζονται ασυνέχειες στην παράγωγο της διαδρομής), παρεμβάλλονται τόξα συναρμογής, τα οποία περιορίζουν το ρυθμό μεταβολής της επιτάχυνσης εξασφαλίζοντας τη βαθμιαία αύξηση της κεντρομόλου επιτάχυνσης (ή ισοδύναμα της καμπυλότητας της διαδρομής) στην τιμή που αντιστοιχεί στην ακτίνα του κύκλου καμπυλότητας και την προδιαγεγραμμένη εφαπτομενική (στην καμπύλη) συνιστώσα της ταχύτητας.
Το θεωρητικό βέλτιστο σχήμα καμπύλης ενός τόξου συναρμογής επιτυγχάνεται με την κλωθοειδή καμπύλη (γνωστή και ως σπειροεδές ή σπείρα του Ώυλερ (Γερμ. Euler)), η οποία διαθέτει την ιδιότητα ότι ένα σώμα που κινείται πάνω της να αυξάνεται η επιτάχυνσή του γραμμικά, δηλ. η κίνησή του να παρουσιάζει σταθερό ρυθμό μεταβολής της επιτάχυνσης. Κατά τη χάραξη σιδηροδρόμων, συνιστάται κατά κανόνα μία μέγιστη τιμή ρυθμού μεταβολής της επιτάχυνσης των 0.5 m/s3 ενώ μια τυπική (σχεδιαστικά) αποδεκτή τιμή είναι τα 0.35 m/s3. Η εικόνα δείχνει ένα τόξο κλωθοειδούς καμπύλης, το οποίο αποτελεί το τόξο συναρμογής μεταξύ ενός ευθύγραμμου τμήματος και ενός κυκλικού τόξου.
Στην πραγματικότητα, το επίπεδο μίας σιδηροδρομικής γραμμής είναι κεκλιμένο κατά μήκος του καμπύλου τόξου και έτσι πρέπει να λαμβάνεται υπ' όψιν και η κάθετη συνιστώσα της επιτάχυνσης που είναι αναγκαία για την ανύψωση του κέντρου μάζας της άμαξας, για την ελαχιστοποίηση της φθοράς στο επίχωμα και στις σιδηροτροχιές, και έτσι στην πράξη χρησιμοποιείται ένα ελαφρώς διαφορετικού σχήματος τόξο. Ένα τέτοιο παράδειγμα τόξου έχει κατοχυρωθεί ως «Τόξο της Βιέννης».[2][3]
Οι τροχιές που ακολουθούν τα γνωστά «τραινάκα του ιλίγγου» στα ψυχαγωγικά θεματικά πάρκα[1] είναι άλλη μία περίπτωση εμφάνισης αυτού του είδους σχεδιαστικών προβλημάτων π.χ. κατά την είσοδο ενός αμαξιδίου σε ένα κυκλικό βρόχο. Τα αμαξίδια σε αυτές τις περιπτώσεις υπόκεινται σε επιταχύνσεις έως και 4g και θα ήταν αδύνατο να κινηθούν μέσα σε κυκλικούς βρόχους χωρίς τη χρήση τόξων προσαρμογής, όπως είναι αδύνατο για ένα σώμα να κινηθεί ομαλά εντός μίας τροχιάς σχήματος οκτώ που να αποτελείται από δύο κύκλους. Κάθε τροχιά που ακολουθεί μία σιγμοειδή καμπύλη πρέπει να περιλαμβάνει τόξα προσαρμογής ώστε να είναι ελεγχόμενος ο ρυθμός μεταβολής της επιτάχυνσης των σωμάτων που κινούνται εντός της.
Στα συστήματα ελέγχου[Επεξεργασία | επεξεργασία κώδικα]
Στα συστήματα ελέγχου κίνησης όπου το ενδιαφέρον εστιάζεται στην κίνηση πάνω σε ευθεία γραμμή, το ζητούμενο είναι να μετακινηθεί ένα σώμα από ένα σταθερό σημείο σε ένα άλλο π.χ. η κίνηση μίας αμαξοστοιχίας ανάμεσα σε δύο σταθμούς πάνω σε ένα σιδηρόδρομο, η πλεύση ενός πορθμείου ανάμεσα σε δύο αγγυροβόλια κλπ. Συνεπώς, ένα σημαντικό κριτήριο σχεδίασης σε αυτές τις περιπτώσεις είναι ο ρυθμός μεταβολής της επιτάχυνσης να βρίσκεται υπό έλεγχο. Τυπικές εφαρμογές είναι οι ελεγκτικοί μηχανισμοί ανελκυστήρων, μηχανημάτων στις μηχανουργικές κατεργασίες κλπ. Είναι γνωστό[4] ότι για τους περισσότερους επιβάτες ένας ρυθμός μεταβολής της επιτάχυνσης των 2.0 m/s3 στην κατακόρυφη κίνηση ενός ανελκυστήρα, θεωρείται ανεκτός ενώ των 6.0 m/s3 ως απαράδεκτος και σε ένα νοσοκομειακό περιβάλλον συνιστάται η ένας ρυθμός μικρότερος των 0.7 m/s3. Σε κάθε περίπτωση, ο περιορισμός ρυθμού μεταβολής της επιτάχυνσης είναι απαραίτητος για την άνετη μετακίνηση.[5] Στο διεθνές πρότυπο ISO 18 738[6] καθορίζεται το πώς μπορεί να μετρηθεί η ποιότητα κύλισης ενός ανελκυστήρα με κριτήριο το ρυθμό μεταβολής της επιτάχυνσης, την επιτάχυνση, τις δονήσεις και το θόρυβο αλλά δεν επιχειρείται ο προσδιορισμός των διαφορετικών επίπεδων ποιότητας της κύλισης ανελκυστήρων.
Για το συντομότερο χρόνο μετακίνησης παρουσία συγκεκριμένων ορίων ταχύτητας, επιτάχυνσης και ρυθμού μεταβολής της επιτάχυνσης, είναι αναγκαία μία (πολυωνυμική) συνάρτηση θέσης τρίτου βαθμού, όπου οι φάσεις αύξησης και μείωσης της ταχύτητας είναι δευτέρου βαθμού, όπως φαίνεται στο παρακάτω γράφημα:
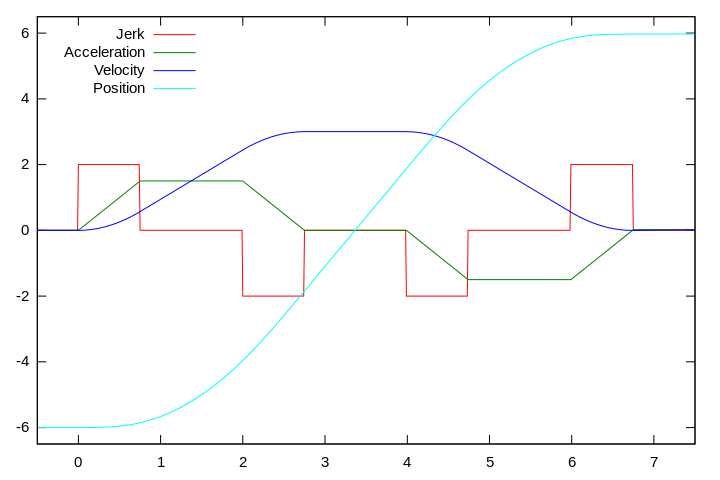
Η κίνηση του σώματος επομένως χαρακτηρίζεται από το πολύ επτά διακριτά στάδια (εφ' όσον τα όρια είναι τέτοια και η απόσταση των δύο σημείων μεταξύ τους είναι τέτοια που να το επιτρέπουν):
- αύξηση επιτάχυνσης: ο περιορισμός του ρυθμού μεταβολής της επιτάχυνσης συνεπάγεται ότι αυτός λαμβάνει τη μέγιστη θετική τιμή του και παραμένει σταθερός πράγμα που σημαίνει γραμμική αύξηση της επιτάχυνσης έως ότου αυτή λάβει τη μέγιστη θετική τιμή της και τετραγωνική αύξηση της ταχύτητας
- οριακή επιτάχυνση: ο ρυθμός μεταβολής της επιτάχυνσης είναι μηδενικός και επομένως η επιτάχυνση είναι σταθερή και η ταχύτητα παρουσιάζει γραμμική αύξηση
- μείωση επιτάχυνσης: ο ρυθμός μεταβολής της επιτάχυνσης λαμβάνει τη μέγιστη αρνητική τιμή του και παραμένει σταθερός πράγμα που σημαίνει γραμμική μείωση της επιτάχυνσης έως ότου αυτή γίνει μηδενική και τετραγωνική αύξηση της ταχύτητας έως ότου λάβει τη μέγιστη θετική τιμή της
- οριακή ταχύτητα: τόσο ο ο ρυθμός μεταβολής της επιτάχυνσης όσο και η επιτάχυνση είναι μηδενκές και άρα η ταχύτητα παραμένει σταθερή
- αύξηση επιβράδυνσης: ο ρυθμός μεταβολής της επιτάχυνσης λαμβάνει τη μέγιστη αρνητική τιμή του και παραμένει σταθερός πράγμα που σημαίνει γραμμική μείωση της επιτάχυνσης έως ότου αυτή λάβει τη μέγιστη αρνητική τιμή της και τετραγωνική μείωση της ταχύτητας
- οριακή επιβράδυνση: ο ρυθμός μεταβολής της επιτάχυνσης είναι μηδενικός και επομένως η επιβράδυνση είναι σταθερή και η ταχύτητα παρουσιάζει γραμμική μείωση
- μείωση επιβράδυνσης: ο ρυθμός μεταβολής της επιτάχυνσης λαμβάνει τη μέγιστη θετική τιμή του και παραμένει σταθερός πράγμα που σημαίνει γραμμική αύξηση της επιτάχυνσης έως ότου αυτή γίνει μηδενική και τετραγωνική μείωση της ταχύτητας έως ότου αυτή γίνει μηδενική τη στιγμή που το σώμα φτάσει στο σημείο προορισμού
Η διάρκεια του τέταρτου σταδίου ή το αν θα παρουσιαστεί καθόλου εξαρτάται την απόσταση μεταξύ των δύο σημείων. Εάν αυτή είναι ίση με κάποια συγκεκριμένη οριακή τιμή, τότε το τέταρτο στάδιο δεν θα παρουσιαστεί και το σώμα θα λάβει τη μέγιστη οριακή ταχύτητα μόνο στιγμιαία. Εάν η απόσταση είναι μικρότερη από αυτήν την οριακή τιμή αλλά μεγαλύτερη από μία δεύτερη οριακή τιμή, το σώμα δε θα φτάσει τη μέγιστη οριακή ταχύτητα και η χρονική διάρκεια των σταδίων 2 και 6 θα μειωθεί ισόποσα. Εάν η απόσταση είναι ίση με τη δεύτερη οριακή τιμή, τότε τα στάδια 2 και 6 δεν θα εμφανιστούν. Εάν η απόσταση είναι μικρότερη από αυτήν την τιμή αλλά μεγαλύτερη από μία τρίτη οριακή τιμή, τότε τα στάδια 1,3,5 και 7 θα μειωθούν ισόποσα και το σώμα δεν θα φτάσει ποτέ τις οριακές επιταχύνσεις. Εάν η απόσταση είναι ακόμη μικρότερη, τότε το σώμα δεν θα φτάσει στον προορισμό με τους ισχύοντες περιορισμούς.
Υπάρχουν επίσης και άλλες στρατηγικές για το σχεδιασμό των χαρακτηριστικών μίας κίνησης, π. χ. ελαχιστοποίηση του τετραγώνου του ρυθμού μεταβολής της επιτάχυνσης για ένα δεδομένο χρόνο μετάβασης, που επιλέγονται για εφαρμογή σε μηχανήματα, μέσα μεταφοράς ανθρώπων, βαρούλκα, αυτοκινητοβιομηχανίες, ρομπότ και πολλά άλλα. Για κίνηση με ημιτονοειδή επιτάχυνση, ημιτονοειδή ταχύτητα και πεπερασμένο ρυθμό μεταβολής επιτάχυνσης βλ. παραπάνω.
Στη μεταποίηση[Επεξεργασία | επεξεργασία κώδικα]
Ο ρυθμός μεταβολής της επιτάχυνσης είναι σημαντικό να εξετάζεται στις διαδικασίες μεταποίησης. Για παράδειγμα, οι ραγδαίες μεταβολές κατά την επιτάχυνση ενός εργαλείου κοπής μπορεί να οδηγήσουν στην πρόωρη φθορά του που με τη σειρά της μπορεί να έχει ως αποτέλεσμα ανωμαλίες κατά την κοπή. Γι' αυτό το λόγο, οι σύγχρονοι ελεγκτές κίνησης περιλαμβάνουν στοιχεία περιορισμού του ρυθμού μεταβολής της επιτάχυνσης. Στη μηχανολογία, ο ρυθμός μεταβολής της επιτάχυνσης, εκτός από την ταχύτητα και την επιτάχυνση, λαμβάνεται υπ' όψιν και κατά τη σχεδίαση του σχήματος των εκκεντροφόρων αξόνων εξαιτίας τόσο των τριβολογικών επιπτώσεων όσο και της ανάγκης για την εξασφάλιση την ικανότητας του εφαπτόμενου σώματος να ακολουθήσει την έκκεντρη τροχιά, χωρίς να διακόπτεται η επαφή του με τον εκκεντροφόρο ή να δημιουργούνται μηχανικές ταλαντώσεις.[7] Ο ρυθμός μεταβολής της επιτάχυνσης πρέπει να λαμβάνεται υπ' όψιν όταν η ένταση των δονήσεων θεωρείται υπερβολική. Για τη μέτρηση του ρυθμού μεταβολής της επιτάχυνσης χρησιμοποιούνται ειδικοί αισθητήρες.
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- Επιτάχυνση της επιτάχυνσης, παράγωγος του ρυθμού μεταβολής της επιτάχυνσης
- Δύναμη Άμπραχαμ-Λώρεντζ (Αγγλ. Abraham–Lorentz), δύναμη στην ηλεκτροδυναμική, το μέγεθος της οποίας είναι ανάλογη του ρυθμού μεταβολής της επιτάχυνσης
- Κρουστική ώση (μηχανική)
- Θεωρία απορρόφησης Γουήλερ-Φάυνμαν (Αγγλ. AbrahamWheeler–Feynman)
Σημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 «How Things Work: Roller Coasters - The Tartan Online». Thetartan.org. 16 Απριλίου 2007. Ανακτήθηκε στις 15 Σεπτεμβρίου 2013.
- ↑ https://depatisnet.dpma.de/DepatisNet/depatisnet?window=1&space=menu&content=treffer&action=pdf&docid=AT000000412975B
- ↑ «Αρχειοθετημένο αντίγραφο» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 13 Μαρτίου 2016. Ανακτήθηκε στις 10 Νοεμβρίου 2016.
- ↑ Howkins, Roger E. «Elevator Ride Quality - The Human Ride Experience». VFZ-Verlag für Zielgruppeninformationen GmbH & Co. KG. Αρχειοθετήθηκε από το πρωτότυπο στις 14 Μαρτίου 2015. Ανακτήθηκε στις 31 Δεκεμβρίου 2014.
- ↑ «Αρχειοθετημένο αντίγραφο» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 26 Αυγούστου 2014. Ανακτήθηκε στις 10 Νοεμβρίου 2016.
- ↑ ISO 18738-1:2012. «Measurement of ride quality -- Part 1: Lifts (elevators)». International Organization for Standardization. Ανακτήθηκε στις 31 Δεκεμβρίου 2014.
- ↑ Blair, G., "Making the Cam", Race Engine Technology 10, September/October 2005
Αναφορές[Επεξεργασία | επεξεργασία κώδικα]
- Sprott JC (2003). Chaos and Time-Series Analysis. Oxford University Press. ISBN 0-19-850839-5.
- Sprott JC (1997). «Some simple chaotic jerk functions» (PDF). Am J Phys 65 (6): 537–43. doi:. Bibcode: 1997AmJPh..65..537S. http://sprott.physics.wisc.edu/pubs/paper229.pdf. Ανακτήθηκε στις 2009-09-28.
- Blair G (2005). «Making the Cam» (PDF). Race Engine Technology (010). http://www.profblairandassociates.com/pdfs/Camshaft%20RET%20010.pdf. Ανακτήθηκε στις 2009-09-29.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Οι έννοιες «jerk», «snap», «crackle» και «pop» στη φυσική
- What is the term used for the third derivative of position?, περιγραφή του ρυθμού μεταβολής της επιτάχυνσης στο Usenet Physics FAQ
- Jerk, snap, and the cosmological equation of state, (Matt Visser)
- Cosmic Jerk, Snap and Beyond, (Maciej Dunajski, Gary Gibbons)
- Mathematics of Motion Control Profiles
- Elevator ride quality
- Elevator manufacturer brochure
- Patent of Wiener Kurve
- Description of Wiener Kurve
| Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα Jerk (physics) της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 4.0. (ιστορικό/συντάκτες). |





































