Χρονολογικές Σειρές

Μια χρονολογική σειρά είναι μια σειρά σημείων δεδομένων με ευρετηρίαση (είτε εισηγμένη είτε διαγραμμισμένη) με χρονοσειρά. Συχνότερα, μια χρονολογική σειρά είναι μια ακολουθία που λαμβάνεται σε διαδοχικά ισαπέχουσες χρονικές στιγμές. Έτσι είναι μια ακολουθία δεδομένων διακριτού χρόνου. Παραδείγματα χρονολογικών σειρών είναι τα ύψη των παλιρροιών των ωκεανών, οι μετρήσεις των ηλιακών κηλίδων και η ημερήσια τιμή κλεισίματος του Dow Jones Industrial Average .
Οι χρονολογικές σειρές παρουσιάζονται πολύ συχνά μέσω γραφημάτων γραμμών. Οι χρονολογικές σειρές χρησιμοποιούνται στην στατιστική, στην επεξεργασία σήματος, στην αναγνώριση μοτίβων, στην οικονομετρία, στα μαθηματικά οικονομικών, στην πρόγνωση καιρού, στην σεισμική πρόβλεψη, στο ηλεκτροεγκεφαλογράφημα, στη μηχανική ελέγχου, στην αστρονομία, στην μηχανική επικοινωνιών και σε μεγάλο βαθμό σε οποιοδήποτε τομέα των εφαρμοσμένων επιστημών και της μηχανικής που περιλαμβάνει χρονικές μετρήσεις.
Η ανάλυση χρονολογικών σειρών περιλαμβάνει μεθόδους για την ανάλυση δεδομένων χρονοσειρών προκειμένου να εξαχθούν σημαντικά στατιστικά στοιχεία και άλλα χαρακτηριστικά των δεδομένων. Η πρόβλεψη χρονολογικών σειρών είναι η χρήση ενός μοντέλου για την πρόβλεψη μελλοντικών τιμών βάσει προηγούμενων τιμών. Ενώ η ανάλυση παλινδρόμησης χρησιμοποιείται συχνά με τέτοιο τρόπο ώστε να ελέγχει τις θεωρίες που υποστηρίζουν ότι οι τρέχουσες τιμές μιας ή περισσότερων ανεξάρτητων χρονοσειρών επηρεάζουν την τρέχουσα τιμή μιας άλλης χρονοσειράς, αυτός ο τύπος ανάλυσης των χρονοσειρών δεν ονομάζεται "ανάλυση χρονοσειρών", η οποία επικεντρώνεται στη σύγκριση τιμών μιας μόνο χρονοσειράς ή πολλαπλών εξαρτημένων χρονοσειρών σε διαφορετικά χρονικά σημεία. [1]Η ανάλυση των διακοπτόμενων χρονοσειρών είναι η ανάλυση των παρεμβάσεων σε μία μόνο χρονολογική σειρά.
Τα δεδομένα των χρονοσειρών έχουν μια φυσική χρονική διάταξη. Αυτό κάνει την ανάλυση των χρονολογικών σειρών διακριτή από τις διατομεακές μελέτες, στις οποίες δεν υπάρχει φυσική διάταξη των παρατηρήσεων (π.χ. η επεξήγηση των μισθών των ανθρώπων σε σχέση με τα αντίστοιχα επίπεδα εκπαίδευσης, όπου τα δεδομένα των ατόμων θα μπορούσαν να εισαχθούν με οποιαδήποτε σειρά). Η ανάλυση χρονολογικών σειρών διακρίνεται επίσης από την ανάλυση χωρικών δεδομένων, όπου οι παρατηρήσεις σχετίζονται συνήθως με γεωγραφικές τοποθεσίες (π.χ. τα λογιστικά δεδομένα για τις τιμές των κατοικιών με βάση τη τοποθεσία καθώς και τα εγγενή χαρακτηριστικά των κατοικιών). Ένα στοχαστικό μοντέλο για μια χρονολογική σειρά θα αντικατοπτρίζει γενικά το γεγονός ότι οι παρατηρήσεις που βρίσκονται κοντά στο χρόνο θα είναι πιο στενά συνδεδεμένες από τις παρατηρήσεις που διαχωρίζονται περαιτέρω. Επιπλέον, τα μοντέλα χρονολογικών σειρών θα χρησιμοποιούν συχνά τη φυσική μονόδρομη διάταξη του χρόνου, έτσι ώστε οι τιμές για μια δεδομένη περίοδο να εκφράζονται σαν να προέρχονται κατά κάποιο τρόπο από προηγούμενες τιμές και όχι από μελλοντικές τιμές (βλέπε αναστρεψιμότητα χρόνου).
Η ανάλυση της χρονοσειράς μπορεί να εφαρμοστεί σε πραγματικά, αξιόπιστα και συνεχή δεδομένα, διακεκριμένα αριθμητικά δεδομένα ή διακριτά συμβολικά δεδομένα (δηλαδή αλληλουχίες χαρακτήρων, όπως γράμματα και λέξεις στην αγγλική γλώσσα[2]).
Μέθοδοι ανάλυσης
[Επεξεργασία | επεξεργασία κώδικα]Οι μέθοδοι για την ανάλυση των χρονολογικών σειρών μπορούν να χωριστούν σε δύο κατηγορίες: μέθοδοι τομέα συχνοτήτων και μέθοδοι χρονικού τομέα. Οι πρώτες περιλαμβάνουν τη φασματική ανάλυση και την ανάλυση κύματος. οι τελευταίες περιλαμβάνουν ανάλυση αυτοσυσχέτισης και διασταυρούμενης συσχέτισης. Στο χρονικό πεδίο, η συσχέτιση και η ανάλυση μπορούν να γίνουν με τρόπο παρόμοιο με φίλτρο, χρησιμοποιώντας κλίμακα συσχέτισης, ελαχιστοποιώντας έτσι την ανάγκη να λειτουργούν στον τομέα συχνοτήτων.
Επιπλέον, οι τεχνικές ανάλυσης χρονοσειρών μπορούν να χωριστούν σε παραμετρικές και μη παραμετρικές μεθόδους. Οι παραμετρικές προσεγγίσεις υποθέτουν ότι η υποκείμενη στατική στοχαστική διαδικασία έχει μια συγκεκριμένη δομή η οποία μπορεί να περιγραφεί με τη χρήση ενός μικρού αριθμού παραμέτρων (για παράδειγμα, χρησιμοποιώντας ένα μοντέλο αυτόματης αντιστροφής ή κινούμενου μέσου όρου). Σε αυτές τις προσεγγίσεις, στόχος είναι να εκτιμηθούν οι παράμετροι του μοντέλου που περιγράφει τη στοχαστική διαδικασία. Αντίθετα, οι μη παραμετρικές προσεγγίσεις εκτιμούν ρητά τη συνδιακύμανση ή το φάσμα της διαδικασίας χωρίς να υποθέσουμε ότι η διαδικασία έχει κάποια συγκεκριμένη δομή.
Οι μέθοδοι της ανάλυσης χρονολογικών σειρών μπορούν επίσης να χωριστούν σε γραμμικές και μη γραμμικές, και σε μονομερείς και πολυπαραγοντικές .
Δεδομένα πίνακα
[Επεξεργασία | επεξεργασία κώδικα]Μια χρονολογική σειρά είναι ένας τύπος δεδομένων πίνακα. Τα δεδομένα πίνακα είναι η γενική κλάση, ένα πολυδιάστατο σύνολο δεδομένων, ενώ ένα σύνολο δεδομένων χρονοσειρών είναι ένα μονοδιάστατο πλαίσιο (όπως ένα σετ δεδομένων διατομής). Ένα σύνολο δεδομένων μπορεί να εμφανίζει χαρακτηριστικά τόσο των δεδομένων πίνακα όσο και των δεδομένων χρονοσειρών. Ένας τρόπος για να τα ξεχωρίσουμε είναι να αναρωτηθούμε τι κάνει ένα αρχείο δεδομένων μοναδικό από τα άλλα αρχεία. Εάν η απάντηση είναι το πεδίο δεδομένων χρόνου, τότε πρόκειται για υποψήφιο σύνολο δεδομένων χρονοσειρών. Αν ο προσδιορισμός μιας μοναδικής εγγραφής απαιτεί ένα πεδίο δεδομένων χρόνου και ένα πρόσθετο αναγνωριστικό που δεν έχει σχέση με το χρόνο (αναγνωριστικό σπουδαστή, σύμβολο μετοχών, κωδικός χώρας), τότε είναι υποψήφιος για δεδομένα πίνακα. Αν η διαφοροποίηση έγκειται στο μη αναγνωριστικό χρόνου, τότε το σύνολο δεδομένων είναι υποψήφιο σύνολο διασταυρούμενων δεδομένων.
Ανάλυση
[Επεξεργασία | επεξεργασία κώδικα]Υπάρχουν διάφοροι τύποι κινήτρων και ανάλυσης δεδομένων για χρονολογικές σειρές που είναι κατάλληλες για διαφορετικούς σκοπούς κλπ.
Κίνητρο
[Επεξεργασία | επεξεργασία κώδικα]Στο πλαίσιο της στατιστικής, της οικονομετρίας, της ποσοτικής χρηματοδότησης, της σεισμολογίας, της μετεωρολογίας και της γεωφυσικής, ο πρωταρχικός στόχος της ανάλυσης χρονοσειρών είναι η πρόβλεψη. Στο πλαίσιο της επεξεργασίας σήματος, της μηχανικής ελέγχου και της μηχανικής επικοινωνίας χρησιμοποιείται για την ανίχνευση και εκτίμηση σημάτων, ενώ στο πλαίσιο της εξόρυξης δεδομένων, της αναγνώρισης προτύπων και της μηχανικής μάθησης ανάλυσης χρονοσειρών μπορεί να χρησιμοποιηθεί για την ομαδοποίηση, για την ταξινόμηση, για τα ερωτήματα με βάση το περιεχόμενο, για την ανίχνευση ανωμαλιών καθώς και την πρόβλεψη.
Διερευνητική ανάλυση
[Επεξεργασία | επεξεργασία κώδικα]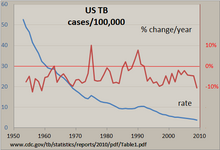
Ο πιο ξεκάθαρος τρόπος για να εξετάσετε χειροκίνητα μια κανονική χρονολογική σειρά είναι με ένα γράφημα γραμμών, όπως αυτό που παρουσιάστηκε για τη φυματίωση στις Ηνωμένες Πολιτείες Αμερικής, που έγινε με ένα πρόγραμμα υπολογιστικών φύλλων. Ο αριθμός των περιπτώσεων τυποποιήθηκε σε ποσοστό ανά 100.000 και υπολογίστηκε η εκατοστιαία μεταβολή ανά έτος σε αυτό το ποσοστό. Η σχεδόν σταθερή γραμμή δείχνει ότι η συχνότητα εμφάνισης της φυματίωσης μειώθηκε στα περισσότερα χρόνια, αλλά η ποσοστιαία μεταβολή αυτού του ποσοστού κυμαινόταν κατά +/- 10%, με «επιταχύνσεις» το 1975 και γύρω στις αρχές της δεκαετίας του 1990. Η χρήση και των δύο κάθετων αξόνων επιτρέπει τη σύγκριση δύο χρονοσειρών σε ένα γράφημα.
Άλλες τεχνικές περιλαμβάνουν:
- Ανάλυση αυτοσυσχέτισης για την εξέταση σειριακής εξάρτησης
- Φασματική ανάλυση για την εξέταση της κυκλικής συμπεριφοράς που δεν χρειάζεται να σχετίζεται με την εποχικότητα. Για παράδειγμα, η δραστηριότητα της ηλιακής κηλίδας ποικίλει σε κύκλους 11 ετών.[3][4] Άλλα κοινά παραδείγματα είναι τα ουράνια φαινόμενα, τα καιρικά πρότυπα, η νευρωτική δραστηριότητα, οι τιμές των βασικών προϊόντων και η οικονομική δραστηριότητα.
- Διαχωρισμός σε στοιχεία που αντιπροσωπεύουν τάση, εποχικότητα, αργή και γρήγορη διακύμανση και κυκλική παρατυπία: δείτε εκτίμηση τάσεων και αποσύνθεση χρονικών σειρών
Τοποθέτηση καμπύλης
[Επεξεργασία | επεξεργασία κώδικα]Η τοποθέτηση καμπύλης[5][6] είναι η διαδικασία κατασκευής μιας καμπύλης ή μαθηματικής συνάρτησης που έχει την καλύτερη προσαρμογή σε μια σειρά σημείων δεδομένων,[7] ενδεχομένως υπόκειται σε περιορισμούς.[8][9] Η προσαρμογή της καμπύλης μπορεί να περιλαμβάνει είτε παρεμβολή,[10][11] όπου απαιτείται ακριβής προσαρμογή στα δεδομένα, είτε εξομάλυνση,[12] [13] στην οποία κατασκευάζεται μια "ομαλή" λειτουργία που ταιριάζει κατά προσέγγιση με τα δεδομένα. Ένα σχετικό θέμα είναι η ανάλυση παλινδρόμησης,[14] [15] η οποία επικεντρώνεται περισσότερο στα ζητήματα στατιστικών συμπερασμάτων, όπως είναι η αβεβαιότητα που υπάρχει σε μια καμπύλη που ταιριάζει στα δεδομένα που παρατηρούνται με τυχαία σφάλματα. Οι προσαρμοσμένες καμπύλες μπορούν να χρησιμοποιηθούν ως βοήθημα για την απεικόνιση των δεδομένων[16][17] για να συναχθούν τιμές μιας συνάρτησης όπου δεν υπάρχουν διαθέσιμα δεδομένα[18] και να συνοψιστούν οι σχέσεις μεταξύ δύο ή περισσοτέρων μεταβλητών.[19] Η παρέκταση αναφέρεται στη χρήση μίας προσαρμοσμένης καμπύλης πέρα από το εύρος των παρατηρηθέντων δεδομένων[20] και υπόκειται σε κάποιο βαθμό αβεβαιότητας[21] επειδή μπορεί να αντικατοπτρίζει τη μέθοδο που χρησιμοποιείται για την κατασκευή της καμπύλης όσο αντανακλά τα παρατηρούμενα δεδομένα .
Η κατασκευή οικονομικών χρονοσειρών περιλαμβάνει την εκτίμηση ορισμένων στοιχείων για ορισμένες ημερομηνίες με παρεμβολή μεταξύ τιμών ("σημείων αναφοράς") για προηγούμενες και μεταγενέστερες ημερομηνίες. Η παρεμβολή είναι η εκτίμηση μιας άγνωστης ποσότητας μεταξύ δύο γνωστών ποσοτήτων (ιστορικά δεδομένα) ή η εξαγωγή συμπερασμάτων σχετικά με τις ελλείπουσες πληροφορίες από τις διαθέσιμες πληροφορίες ("ανάγνωση μεταξύ των γραμμών").[22] Η παρεμβολή είναι χρήσιμη όταν είναι διαθέσιμα τα δεδομένα που περιβάλλουν τα ελλείποντα δεδομένα και είναι γνωστή η τάση, η εποχικότητα και οι μακροπρόθεσμοι κύκλοι. Αυτό γίνεται συχνά χρησιμοποιώντας μια σχετική σειρά γνωστή για όλες τις σχετικές ημερομηνίες.[23] Εναλλακτικά, χρησιμοποιείται πολυωνυμική παρεμβολή ή παρεμβολή spline, όπου οι τετραγωνικές πολυωνυμικές συναρτήσεις ταιριάζουν σε χρονικά διαστήματα ώστε να ταιριάζουν ομαλά μεταξύ τους. Ένα διαφορετικό πρόβλημα που σχετίζεται στενά με την παρεμβολή είναι η προσέγγιση μιας περίπλοκης λειτουργίας με μια απλή συνάρτηση (που ονομάζεται επίσης παλινδρόμηση). Η κύρια διαφορά μεταξύ της παλινδρόμησης και της παρεμβολής είναι ότι η πολυωνυμική παλινδρόμηση δίνει ένα ενιαίο πολυώνυμο που μοντελοποιεί ολόκληρο το σύνολο δεδομένων. Η παρεμβολή Spline, ωστόσο, αποδίδει μια συνεχή λειτουργία κατά τμήματα που αποτελείται από πολλά πολυώνυμα για να μοντελοποιήσει το σύνολο δεδομένων.
Η παρέκταση είναι η διαδικασία εκτίμησης, πέραν του αρχικού εύρους παρατήρησης, της τιμής μιας μεταβλητής με βάση τη σχέση της με μια άλλη μεταβλητή. Είναι παρόμοιο με την παρεμβολή, η οποία παράγει εκτιμήσεις μεταξύ γνωστών παρατηρήσεων, αλλά η παρέκταση υπόκειται σε μεγαλύτερη αβεβαιότητα και υψηλότερο κίνδυνο να παράγει άχρηστα αποτελέσματα.
Προσέγγιση Συνάρτησης
[Επεξεργασία | επεξεργασία κώδικα]Γενικά, ένα πρόβλημα προσέγγισης συνάρτησης μας ζητά να επιλέξουμε μια συνάρτηση ανάμεσα σε μια καλά καθορισμένη κλάση που να ταιριάζει απόλυτα ("προσεγγίζει") μια συνάρτηση στόχου με έναν συγκεκριμένο τρόπο εργασίας. Μπορούμε να διακρίνουμε δύο μεγάλες κατηγορίες προβλημάτων προσέγγισης συνάρτησης: Πρώτον, για τις γνωστές συναρτήσεις στόχου η θεωρία προσέγγισης είναι ο κλάδος της αριθμητικής ανάλυσης που διερευνά τον τρόπο με τον οποίο ορισμένες γνωστές συναρτήσεις (για παράδειγμα, ειδικές συναρτήσεις) μπορούν να προσεγγιστούν από μια συγκεκριμένη κατηγορία συναρτήσεων, πολυώνυμα ή ορθολογικές συναρτήσεις) που συχνά έχουν επιθυμητές ιδιότητες (φθηνός υπολογισμός, συνέχεια, ενσωματωμένες και οριακές τιμές κλπ.).
Δεύτερον, η συνάρτηση στόχου, την αποκαλούμε g , μπορεί να είναι άγνωστη: αντί ενός ρητού τύπου, μόνο ένα σύνολο σημείων (μια χρονοσειρά) τύπου (x, g (x)) παρέχεται. Ανάλογα με τη δομή του τομέα και την κωδικομετρία g, μπορούν να εφαρμοστούν διάφορες τεχνικές για την προσέγγιση της g. Για παράδειγμα, εάν το g είναι μια πράξη με πραγματικούς αριθμούς, μπορούν να χρησιμοποιηθούν τεχνικές παρεμβολής, παρέκτασης, ανάλυσης παλινδρόμησης και προσαρμογής καμπύλης. Εάν η κωδικομετρία (εύρος ή σύνολο στόχων) του g είναι ένα πεπερασμένο σύνολο, τότε έχουμε να κάνουμε με ένα πρόβλημα ταξινόμησης. Ένα σχετικό πρόβλημα της προσέγγισης των χρονικών σειρών σε απευθείας σύνδεση[24] είναι να συνοψίσουμε τα δεδομένα σε ένα μονοπάτι και να κατασκευάσουμε μια κατά προσέγγιση εκπροσώπηση που μπορεί να υποστηρίξει μια ποικιλία ερωτημάτων χρονοσειρών με όρια στο χειρότερο σφάλμα.
Σε κάποιο βαθμό τα διαφορετικά προβλήματα (παλινδρόμηση, ταξινόμηση, προσέγγιση φυσικής κατάστασης) έλαβαν μια ενοποιημένη αντιμετώπιση στη θεωρία της στατιστικής μάθησης, όπου αντιμετωπίζονται ως επιβλεπόμενα μαθησιακά προβλήματα.
Πρόβλεψη και πρόγνωση
[Επεξεργασία | επεξεργασία κώδικα]Στην στατιστική, η πρόβλεψη αποτελεί μέρος του στατιστικού συμπερασμού. Μια συγκεκριμένη προσέγγιση σε τέτοια συμπεράσματα είναι γνωστή ως πρόβλεψη, αλλά η πρόβλεψη μπορεί να πραγματοποιηθεί μέσα σε οποιαδήποτε από τις διάφορες προσεγγίσεις στη στατιστική εξαγωγή. Πράγματι, μία περιγραφή των στατιστικών είναι ότι παρέχει ένα μέσο μεταφοράς γνώσεων για ένα δείγμα ενός πληθυσμού σε ολόκληρο τον πληθυσμό και σε άλλους συναφείς πληθυσμούς, που δεν είναι απαραιτήτως η ίδια με την πρόβλεψη με την πάροδο του χρόνου. Όταν οι πληροφορίες μεταφέρονται διαχρονικά, συχνά σε συγκεκριμένα χρονικά σημεία, η διαδικασία είναι γνωστή ως πρόγνωση.
- Πλήρως σχηματισμένα στατιστικά μοντέλα για σκοπούς στοχαστικής προσομοίωσης, έτσι ώστε να δημιουργούνται εναλλακτικές εκδόσεις των χρονοσειρών, που να αντιπροσωπεύουν το τι μπορεί να συμβεί σε μη συγκεκριμένες χρονικές περιόδους στο μέλλον
- Απλά ή πλήρως σχηματισμένα στατιστικά μοντέλα για την περιγραφή πιθανού αποτελέσματος των χρονοσειρών στο άμεσο μέλλον, δεδομένης της γνώσης των πιο πρόσφατων αποτελεσμάτων (πρόγνωση).
- Η πρόγνωση σε χρονολογικές σειρές γίνεται συνήθως με τη χρήση αυτοματοποιημένων στατιστικών πακέτων λογισμικού και γλωσσών προγραμματισμού, όπως Mathematica , R, S, SAS, SPSS, Minitab, pandas (Python) και πολλά άλλα.
- Η πρόγνωση σε δεδομένα μεγάλης κλίμακας γίνεται με τη χρήση του Spark, το οποίο έχει το spark-ts ως ένα πακέτο τρίτου.
Ταξινόμηση
[Επεξεργασία | επεξεργασία κώδικα]Αντιστοίχιση μοτίβου χρονολογικών σειρών σε μια συγκεκριμένη κατηγορία, για παράδειγμα, προσδιορίστε μια λέξη που βασίζεται σε σειρά κινήσεων χεριών στη νοηματική γλώσσα.
Εκτίμηση σήματος
[Επεξεργασία | επεξεργασία κώδικα]Αυτή η προσέγγιση βασίζεται στην αρμονική ανάλυση και το φιλτράρισμα σημάτων στον τομέα συχνοτήτων χρησιμοποιώντας τον μετασχηματισμό Fourier και την εκτίμηση της φασματικής πυκνότητας, η ανάπτυξη της οποίας επιταχύνθηκε σημαντικά κατά τη διάρκεια του Β' Παγκοσμίου Πολέμου από τον μαθηματικό Norbert Wiener, τους ηλεκτρολόγους μηχανικούς Rudolf E. Kálmán, Dennis Gabor και άλλους για το φιλτράρισμα σημάτων από τον θόρυβο και την πρόβλεψη των τιμών σήματος σε ένα συγκεκριμένο χρονικό σημείο. Βλέπε φίλτρο Kalman, Θεωρία Εκτίμησης και Ψηφιακή επεξεργασία σήματος
Κατάτμηση
[Επεξεργασία | επεξεργασία κώδικα]Διαχωρίζοντας μια χρονολογική σειρά σε μια ακολουθία τμημάτων. Συχνά συμβαίνει ότι μια χρονοσειρά μπορεί να αναπαρασταθεί ως μια ακολουθία μεμονωμένων τμημάτων, κάθε μία με τις δικές της χαρακτηριστικές ιδιότητες. Για παράδειγμα, το ηχητικό σήμα από μια κλήση συνδιάσκεψης μπορεί να χωριστεί σε κομμάτια που αντιστοιχούν στους χρόνους κατά τους οποίους ο καθένας μιλούσε. Στον κατακερματισμό της χρονικής σειράς, ο στόχος είναι να προσδιοριστούν τα σημεία οριοθέτησης τμήματος της χρονοσειράς και να χαρακτηριστούν οι δυναμικές ιδιότητες που σχετίζονται με κάθε τμήμα. Κάποιος μπορεί να προσεγγίσει αυτό το πρόβλημα χρησιμοποιώντας ανίχνευση σημείου αλλαγής ή με μοντελοποίηση της χρονοσειράς ως πιο εξελιγμένο σύστημα, όπως ένα γραμμικό σύστημα Markov Jump.
Μοντέλα
[Επεξεργασία | επεξεργασία κώδικα]Τα μοντέλα δεδομένων χρονοσειρών μπορούν να έχουν πολλές μορφές και να αντιπροσωπεύουν διαφορετικές στοχαστικές διαδικασίες. Κατά τη μοντελοποίηση παραλλαγών στο επίπεδο μιας διαδικασίας, τρεις ευρείες κατηγορίες πρακτικής σημασίας είναι τα μοντέλα αυτόματης αντιστροφής (AR), τα ολοκληρωμένα μοντέλα (I) και τα μοντέλα κινητού μέσου (MA). Αυτές οι τρεις κατηγορίες εξαρτώνται γραμμικά από τα προηγούμενα σημεία δεδομένων.[25] Οι συνδυασμοί αυτών των ιδεών παράγουν μοντέλα αυτορυθμιζόμενου κινούμενου μέσου (ARMA) και αυτόματης αντιστροφής κινητού μέσου (ARIMA). Το μοντέλο αυτόματης αντιστροφής, κλασματικά ολοκληρωμένου κινούμενου μέσου (ARFIMA), γενικεύει τα πρώτα τρία. Οι επεκτάσεις αυτών των κατηγοριών για την αντιμετώπιση δεδομένων με βάση το διάνυσμα διατίθενται υπό την επικεφαλίδα πολυπαραγοντικών μοντέλων χρονοσειρών και μερικές φορές τα προηγούμενα ακρωνύμια επεκτείνονται συμπεριλαμβάνοντας ένα αρχικό "V" για το "διάνυσμα", όπως στο VAR για την αυτόματη διόρθωση του διανύσματος. Ένα πρόσθετο σύνολο επεκτάσεων αυτών των μοντέλων είναι διαθέσιμο για χρήση όπου η παρατηρούμενη χρονοσειρά οδηγείται από ορισμένες χρονοσειρές "εξωστρέφειας" (που μπορεί να μην έχουν αιτιώδη επίδραση στις παρατηρούμενες σειρές): η διάκριση από την πολυπαραγοντική περίπτωση είναι ότι οι σειρές δύναμης μπορεί να είναι καθοριστικές ή υπό τον έλεγχο του πειραματιστή. Για αυτά τα μοντέλα, τα ακρωνύμια επεκτείνονται με τελικό "Χ" για "εξωγενή".
Η μη γραμμική εξάρτηση του επιπέδου μιας σειράς από προηγούμενα σημεία δεδομένων ενδιαφέρει, εν μέρει λόγω της πιθανότητας δημιουργίας μιας χαοτικής χρονοσειράς. Ωστόσο, το πιο σημαντικό είναι ότι οι εμπειρικές έρευνες μπορούν να υποδείξουν το πλεονέκτημα της χρήσης προβλέψεων προερχόμενων από μη γραμμικά μοντέλα, έναντι εκείνων που προέρχονται από γραμμικά μοντέλα, όπως για παράδειγμα σε μη γραμμικά αυτορυθμιζόμενα εξωγενή μοντέλα. Περαιτέρω αναφορές σε ανάλυση μη γραμμικών χρονοσειρών: (Kantz και Schreiber),[26] και (Abarbanel)[27]
Μεταξύ άλλων τύπων μη γραμμικών μοντέλων χρονολογικών σειρών υπάρχουν μοντέλα που αντιπροσωπεύουν τις μεταβολές της διακύμανσης με την πάροδο του χρόνου (ετεροσκεδαστικότητα). Αυτά τα μοντέλα αντιπροσωπεύουν την αυτοεπαναστατική υπό όρους ετεροσκεδαστικότητα (ARCH) και η συλλογή περιλαμβάνει μια μεγάλη ποικιλία εκπροσώπησης (GARCH, TARCH, EGARCH, FIGARCH, CGARCH, κ.λπ.). Εδώ οι μεταβολές στη μεταβλητότητα σχετίζονται με, ή προβλέπονται από, πρόσφατες προηγούμενες τιμές των παρατηρούμενων σειρών. Αυτό έρχεται σε αντίθεση με άλλες πιθανές παραστάσεις τοπικά μεταβαλλόμενης μεταβλητότητας, όπου η μεταβλητότητα μπορεί να διαμορφώνεται ως οδηγούμενη από μια χωριστή χρονικά μεταβαλλόμενη διαδικασία, όπως σε ένα διπλά στοχαστικό μοντέλο.
Σε πρόσφατες εργασίες για αναλύσεις χωρίς μοντέλο, οι μέθοδοι που βασίζονται σε μετασχηματισμούς μικρών κυμάτων (για παράδειγμα τοπικά σταθερά μικρά κύματα και νεκρά δίκτυα που έχουν αποικοδομηθεί από μικρά κύματα) έχουν κερδίσει την εύνοια. Οι τεχνικές πολλαπλών κλιμάκων (συχνά αναφέρονται ως πολυδιαλύσεις) αποσυνθέτουν μια δεδομένη χρονική σειρά προσπαθώντας να απεικονίσουν την εξάρτηση από το χρόνο σε πολλαπλές κλίμακες. Βλέπε επίσης τεχνικές πολλών φαινομένων (MSMF) Markov switching για την εξέλιξη της μεταβλητότητας του μοντέλου.
Ένα Hidden Markov μοντέλο (HMM) είναι ένα στατιστικό μοντέλο Markov στο οποίο το μοντέλο του συστήματος θεωρείται ότι είναι μια διαδικασία Markov με μη παρατηρημένες (κρυφές) καταστάσεις. Ένα HMM μπορεί να θεωρηθεί ως το πιο απλό δυναμικό Bayesian δίκτυο. Τα μοντέλα HMM χρησιμοποιούνται ευρέως στην αναγνώριση ομιλίας, για τη μετάφραση μιας χρονικής σειράς προφορικών λέξεων σε κείμενο.
Σημειογραφία
[Επεξεργασία | επεξεργασία κώδικα]Χρησιμοποιούνται διάφορες διαφορετικές συμβολισμοί για την ανάλυση χρονοσειρών. Ένας κοινός συμβολισμός που καθορίζει μια χρονοσειρά X που ευρετηριάζεται από τους φυσικούς αριθμούς γράφεται ως
- Χ = {Χ1, Χ2,. ...}.
Ένας άλλος κοινός συμβολισμός είναι ο
- Y = {Yt : t ∈ T},
όπου T το σετ δείκτη.
Συνθήκες
[Επεξεργασία | επεξεργασία κώδικα]Υπάρχουν δύο ομάδες συνθηκών κάτω από τις οποίες βασίζεται μεγάλο μέρος της θεωρίας:
- Στατική διαδικασία
- Εργοδική διαδικασία
Ωστόσο, οι ιδέες της ακινησίας πρέπει να επεκταθούν ώστε να εξεταστούν δύο σημαντικές ιδέες: η αυστηρή στάση και η ακινησία δεύτερης τάξης. Και τα δύο μοντέλα και οι εφαρμογές μπορούν να αναπτυχθούν κάτω από κάθε μία από αυτές τις συνθήκες, αν και τα μοντέλα στην τελευταία περίπτωση μπορεί να θεωρηθούν ως εν μέρει μόνο καθορισμένα.
Επιπλέον, η ανάλυση χρονοσειρών μπορεί να εφαρμοστεί όταν οι σειρές είναι εποχιακά στάσιμες ή μη στάσιμες. Οι περιπτώσεις όπου τα πλάτη των συνιστωσών συχνότητας αλλάζουν με το χρόνο μπορούν να αντιμετωπιστούν με την ανάλυση χρόνου-συχνότητας, η οποία χρησιμοποιεί μια αναπαράσταση χρόνου-συχνότητας μιας χρονικής σειράς ή ενός σήματος.[28]
Εργαλεία
[Επεξεργασία | επεξεργασία κώδικα]Τα εργαλεία για τη διερεύνηση δεδομένων χρονοσειρών περιλαμβάνουν:
- Εξέταση της συνάρτησης αυτοσυσχέτισης και της συνάρτησης φασματικής πυκνότητας (επίσης λειτουργίες διασταυρούμενης συσχέτισης και λειτουργίες διασταυρούμενης φασματικής πυκνότητας)
- Επεκτάσιμες πολλαπλής και αυτόματης συσχέτισης συναρτήσεις για την απομάκρυνση των συνεισφορών των αργών συνιστωσών[29]
- Εκτέλεση μετασχηματισμού Fourier για διερεύνηση της σειράς στον τομέα συχνοτήτων
- Χρήση φίλτρου για την αφαίρεση ανεπιθύμητου θορύβου
- Ανάλυση κύριου συστατικού (ή εμπειρική ανάλυση ορθογώνιας λειτουργίας)
- Ανάλυση μοναδικού φάσματος
- "Δομικά" μοντέλα:
- Γενικά μοντέλα κρατικού διαστήματος
- Μη παρατηρημένα μοντέλα στοιχείων
- Μηχανική μάθηση
- Τεχνητά νευρωνικά δίκτυα
- Υποστήριξη μηχανής φορέα
- Ασαφής λογική
- Gaussian διαδικασία
- Κρυφό μοντέλο Markov
- Ανάλυση θεωρίας ουρών αναμονής
- Χάρτης ελέγχου
- Shewhart άτομα πίνακα ελέγχου
- Διάγραμμα CUSUM
- Διάγραμμα EWMA
- Αναλυτική ανάλυση διακύμανσης
- Δυναμική χρονική στρέβλωση[30]
- Διασταυρούμενη συσχέτιση[31]
- Δυναμικό δίκτυο Bayesian
- Τεχνικές ανάλυσης χρόνου:
- Γρήγορος μετασχηματισμός Fourier
- Συνεχής μετασχηματισμός κύματος
- Σύντομος μετασχηματισμός Fourier
- Μετασχηματισμός Chirplet
- Κλασματικός μετασχηματισμός Fourier
- Χαοτική ανάλυση
- Διάσταση συσχετισμού
- Επαναλαμβανόμενα γραφήματα
- Ανάλυση ποσοτικού προσδιορισμού επαναλήψεων
- Lyapunov εκθέτες
- Κωδικοποίηση εντροπίας
Μέτρα
[Επεξεργασία | επεξεργασία κώδικα]Μετρήσεις χρονολογικών σειρών ή χαρακτηριστικά που μπορούν να χρησιμοποιηθούν για ταξινόμηση χρονοσειρών ή ανάλυση παλινδρόμησης:[32]
- Μονομεταβλητά γραμμικά μέτρα
- Στιγμή (μαθηματικά)
- Φασματική ισχύς μπάντας
- Φασματική ακραία συχνότητα
- Συσσωρευμένη ενέργεια (επεξεργασία σήματος)
- Χαρακτηριστικά της συνάρτησης αυτοσυσχέτισης
- Hjorth παραμέτρους
- Παράμετροι FFT
- Παράμετροι αυτόματης αντιστροφής
- Δοκιμή Mann-Kendall
- Μη μεταβλητά μη γραμμικά μέτρα
- Μέτρα που βασίζονται στο άθροισμα συσχετισμού
- Διάσταση συσχετισμού
- Συσχέτιση ολοκλήρωσης
- Πυκνότητα συσχέτισης
- Εντροπία συσχετισμού
- Κατά προσέγγιση εντροπία [33]
- Δείγμα εντροπίας
- Η εντροπία του Fourier
- Εντροπία Μικρών Κυμάτων
- Εντροπία Rényi
- Μέθοδοι υψηλότερης τάξης
- Περιθωριακή προβλεψιμότητα
- Δείκτης δυναμικής ομοιότητας
- Μέτρα ανισότητας χώρου κατάστασης
- Lyapunov εκθέτης
- Μέθοδοι μετασχηματισμού
- Τοπική ροή
- Άλλα μονομερή μέτρα
- Αλγοριθμική πολυπλοκότητα
- Kolmogorov εκτιμήσεις πολυπλοκότητας
- Hidden Markov Μοντέλο καταστάσεις
- Υπογραφή σκληρής διαδρομής[34]
- Επανάληψη χρονικών σειρών και υποκατάστατων διορθώσεων
- Απώλεια υποτροπής (βαθμός μη στασιμότητας)
- Διμερή γραμμικά μέτρα
- Μέγιστη γραμμική συσχέτιση
- Γραμμική συνοχή (επεξεργασία σήματος)
- Διμερή μη γραμμικά μέτρα
- Μη γραμμική αλληλεξάρτηση
- Δυναμική πρόσκτηση (φυσική)
- Μέτρα συγχρονισμού φάσης
- Μέτρα για το κλείδωμα φάσης
- Μέτρα ομοιότητας:[35]
- Διασταυρούμενη συσχέτιση
- Δυναμική χρονική κάμψη[30]
- Κρυμμένα μοντέλα Markov
- Επεξεργασία απόστασης
- Συνολική συσχέτιση
- Newey-West estimator
- Μετασχηματισμός Prais-Winsten
- Στοιχεία ως διανύσματα σε ένα μετρήσιμο χώρο
- Απόσταση Minkowski
- Απόσταση Mahalanobis
- Δεδομένα ως χρονοσειρές με φακέλους
- Παγκόσμια τυπική απόκλιση
- Τοπική τυπική απόκλιση
- Παρατηρημένη τυπική απόκλιση
- Τα δεδομένα ερμηνεύονται ως στοχαστική σειρά
- Συντελεστής συσχέτισης προϊόντος-στιγμής Pearson
- Συγκριτικός συντελεστής συσχέτισης του Spearman
- Τα δεδομένα ερμηνεύονται ως συνάρτηση κατανομής πιθανοτήτων
- Kolmogorov-Smirnov δοκιμή
- Κριτήριο Cramér-von Mises
Απεικόνιση
[Επεξεργασία | επεξεργασία κώδικα]Οι χρονολογικές σειρές μπορούν να απεικονιστούν με δύο κατηγορίες διαγραμμάτων: Επικαλυπτόμενα διαγράμματα και χωριστά διαγράμματα. Τα επικαλυπτόμενα γραφήματα εμφανίζουν τις συνεχόμενες σειρές με την ίδια διάταξη, ενώ τα χωριστά διαγράμματα τις παρουσιάζουν σε διαφορετικές διατάξεις (αλλά ευθυγραμμισμένες για λόγους σύγκρισης)[36]
Επικαλυπτόμενα γραφήματα
[Επεξεργασία | επεξεργασία κώδικα]- Πλεγμένα γραφήματα
- Γραφήματα γραμμής
- Γραφήματα κλίσης
- GapChart
Διαχωρισμένα διαγράμματα
[Επεξεργασία | επεξεργασία κώδικα]- Γραφήματα Horizon
- Μειωμένο διάγραμμα γραμμής (μικρά πολλαπλάσια)
- Γραφική παράσταση σιλουέτας
- Κυκλικό γράφημα σιλουέτας
Λογισμικό
[Επεξεργασία | επεξεργασία κώδικα]Η εργασία με δεδομένα Χρονολογικών Σειρών είναι μια σχετικά κοινή χρήση για το λογισμικό στατιστικής ανάλυσης. Ως αποτέλεσμα αυτού, υπάρχουν πολλές προσφορές τόσο εμπορικής μορφής όσο και ανοικτού κώδικα μορφής. Μερικά παραδείγματα περιλαμβάνουν:
- Συμπληρωματικό πακέτο στατιστικών στοιχείων CRAN για την R[37]
- Ανάλυση και πρόβλεψη με Weka[38]
- Προγνωστική μοντελοποίηση με το GMDH Shell[39]
- Λειτουργίες και Μοντελοποίηση στη Γλώσσα Wolfram[40]
- Αντικείμενα χρονικής σειράς σε MATLAB[41]
- SAS / ETS σε λογισμικό SAS[42]
- Expert Modeler σε IBM SPSS Statistics και IBM SPSS Modeler
- Αυτόματη πρόβλεψη χρονοσειρών με LDT[43]
- Το EViews είναι ένα στατιστικό πακέτο για τα Windows, το οποίο χρησιμοποιείται κυρίως για την οικονομετρική ανάλυση με βάση τις χρονοσειρές.
- bayesloop: Πιθανό πλαίσιο προγραμματισμού που διευκολύνει την επιλογή αντικειμενικού μοντέλου για μοντέλα παραμέτρων που ποικίλουν χρονικά[44]
- Slycat Web-based πλατφόρμα ανάλυσης και οπτικοποίησης, που δημιουργήθηκε στο Sandia National Laboratories[45]
- Seglearn: πακέτο python ανοιχτού κώδικα και επέκταση scikit-learn για μηχανική μάθηση με δεδομένα χρονοσειρών και ακολουθιών[46]
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]- Anomaly time series
- Chirp
- Decomposition of time series
- Detrended fluctuation analysis
- Digital signal processing
- Distributed lag
- Estimation theory
- Forecasting
- Hurst exponent
- Monte Carlo method
- Panel analysis
- Random walk
- Scaled correlation
- Seasonal adjustment
- Sequence analysis
- Signal processing
- Time series database (TSDB)
- Trend estimation
- Unevenly spaced time series
Βιβλιογραφία
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Imdadullah. «Time Series Analysis». Basic Statistics and Data Analysis. itfeature.com. Ανακτήθηκε στις 2 Ιανουαρίου 2014.
- ↑ Lin, Jessica· Keogh, Eamonn (2003). «A symbolic representation of time series, with implications for streaming algorithms». Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery. New York: ACM Press.
- ↑ Bloomfield, P. (1976). Fourier analysis of time series: An introduction. New York: Wiley. ISBN 0471082562.
- ↑ Shumway, R. H. (1988). Applied statistical time series analysis. Englewood Cliffs, NJ: Prentice Hall. ISBN 0130415006.
- ↑ Sandra Lach Arlinghaus, PHB Πρακτικό εγχειρίδιο της τοποθέτησης καμπύλης. CRC Press, 1994.
- ↑ William M. Kolb. Προσαρμογή καμπύλης για προγραμματιζόμενους αριθμομηχανές. Syntec, Incorporated, 1984.
- ↑ S.S. Halli, K.V. Rao. 1992. Advanced Techniques of Population Analysis. (ISBN 0306439972) Page 165 (cf. ... functions are fulfilled if we have a good to moderate fit for the observed data.)
- ↑ [1] Το σήμα και ο θόρυβος : Γιατί τόσες προβλέψεις αποτυγχάνουν-αλλά μερικοί δεν το κάνουν. Από την Nate Silver
- ↑ Προετοιμασία δεδομένων για εξόρυξη δεδομένων : κείμενο. Από τον Dorian Pyle.
- ↑ Αριθμητικές Μέθοδοι στην Μηχανική με MATLAB®. Από τον Jaan Kiusalaas . Σελίδα 24.
- ↑ Αριθμητικές Μέθοδοι στην Μηχανική με την Python 3 . Από τον Jaan Kiusalaas. Σελίδα 21.
- ↑ Αριθμητικές μέθοδοι διαμόρφωσης καμπύλης . Από την PG Guest, Philip George Guest. Σελίδα 349.
- ↑ Δείτε επίσης: Mollifier
- ↑ Τοποθέτηση μοντέλων σε βιολογικά δεδομένα με γραμμική και μη γραμμική παλινδρόμηση Αρχειοθετήθηκε 2018-08-09 στο Wayback Machine. . Από τον Harvey Motulsky, τον Άρθουρ Χριστόπουλο.
- ↑ Ανάλυση παλινδρόμησης από Rudolf J. Freund, William J. Wilson, Ping Sa. Σελίδα 269.
- ↑ Οπτική Πληροφορική. Επεξεργασία από τον Halimah Badioze Zaman, τον Peter Robinson, τη Μαρία Πέτρου, τον Patrick Olivier, τον Heiko Schröder. Σελίδα 689.
- ↑ Αριθμητικές μέθοδοι για μη γραμμικά μηχανολογικά μοντέλα . Από τον John R. Hauser. Σελίδα 227.
- ↑ Μέθοδοι πειραματικής φυσικής: Φασματοσκοπία, Τόμος 13, Μέρος 1. Από Claire Marton. Σελίδα 150.
- ↑ Encyclopedia of Research Design, Τόμος 1. Επεξεργασία από τον Neil J. Salkind. Σελίδα 266.
- ↑ Κοινοτικές τεχνικές ανάλυσης και προγραμματισμού . Από τον Richard E. Klosterman. Σελίδα 1.
- ↑ Εισαγωγή στον Κίνδυνο και την Αβεβαιότητα στην Αξιολόγηση των Περιβαλλοντικών Επενδύσεων. Εκδόσεις DIANE. Σελ. 69
- ↑ Χαμίνγκ, Ρίτσαρντ. Αριθμητικές μέθοδοι για επιστήμονες και μηχανικούς. Courier Corporation, 2012.
- ↑ Friedman, Milton. " Η παρεμβολή των χρονοσειρών από σχετικές σειρές ." Εφημερίδα της Αμερικανικής Στατιστικής Ένωσης 57.300 (1962): 729-757.
- ↑ Gandhi, Sorabh, Luca Foschini και Subhash Suri. " Διαστημική αποδοτική ηλεκτρονική προσέγγιση των δεδομένων χρονοσειρών: Ρεύματα, αμνησία και εκτός παραγγελίας ." Data Engineering (ICDE), 2010 IEEE 26ο Διεθνές Συνέδριο με θέμα:. IEEE, 2010.
- ↑ Gershenfeld, N. (1999). The Nature of Mathematical Modeling. New York: Cambridge University Press. σελίδες 205–208. ISBN 0521570956.
- ↑ Kantz, Holger· Thomas, Schreiber (2004). Nonlinear Time Series Analysis. London: Cambridge University Press. ISBN 978-0521529020.
- ↑ Abarbanel, Henry (25 Νοεμβρίου 1997). Analysis of Observed Chaotic Data. New York: Springer. ISBN 978-0387983721.
- ↑ Boashash, B. (ed.), (2003) Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Elsevier Science, Oxford, 2003 (ISBN 0-08-044335-4)
- ↑ Nikolić, D.; Muresan, R. C.; Feng, W.; Singer, W. (2012). «Scaled correlation analysis: a better way to compute a cross-correlogram». European Journal of Neuroscience 35 (5): 742–762. doi:.
- ↑ 30,0 30,1 Sakoe, Hiroaki· Chiba, Seibi (1978). «Dynamic programming algorithm optimization for spoken word recognition». IEEE Transactions on Acoustics, Speech, and Signal Processing.
- ↑ Goutte, Cyril· Toft, Peter (1999). «On Clustering fMRI Time Series». NeuroImage.
- ↑ Mormann, Florian; Andrzejak, Ralph G.; Elger, Christian E.; Lehnertz, Klaus (2007). «Seizure prediction: the long and winding road». Brain 130 (2): 314–333. doi:. PMID 17008335.
- ↑ Land, Bruce· Elias, Damian. «Measuring the 'Complexity' of a time series».
- ↑ [1] Chevyrev, Ι., Kormilitzin, Α. (2016) " A Primer για τη μέθοδο υπογραφής στη μηχανική μάθηση , arXiv: 1603.03788v1"
- ↑ Ropella, G. E. P.; Nag, D. A.; Hunt, C. A. (2003). «Similarity measures for automated comparison of in silico and in vitro experimental results». Engineering in Medicine and Biology Society 3: 2933–2936. doi:.
- ↑ Tominski, Christian· Aigner, Wolfgang. «The TimeViz Browser:A Visual Survey of Visualization Techniques for Time-Oriented Data». Ανακτήθηκε στις 1 Ιουνίου 2014.
- ↑ Hyndman, Rob J (2016-01-22). CRAN Task View: Time Series Analysis. https://cran.r-project.org/web/views/TimeSeries.html.
- ↑ «Time Series Analysis and Forecasting with Weka – Pentaho Data Mining – Pentaho Wiki». wiki.pentaho.com. Αρχειοθετήθηκε από το πρωτότυπο στις 22 Νοεμβρίου 2016. Ανακτήθηκε στις 7 Ιουλίου 2016.
- ↑ «Time Series Analysis & Forecasting Software 2016 [Free Download]» (στα Αγγλικά). Ανακτήθηκε στις 7 Ιουλίου 2016.
- ↑ «Time Series—Wolfram Language Documentation». reference.wolfram.com. Ανακτήθηκε στις 7 Ιουλίου 2016.
- ↑ «Time Series Objects – MATLAB & Simulink». www.mathworks.com. Ανακτήθηκε στις 7 Ιουλίου 2016.
- ↑ «Econometrics and Time Series Analysis, SAS/ETS Software». Ανακτήθηκε στις 7 Ιουλίου 2016.
- ↑ «LDT». SourceForge. Ανακτήθηκε στις 4 Σεπτεμβρίου 2016.
- ↑ «bayesloop: Probabilistic programming framework that facilitates objective model selection for time-varying parameter models». Ανακτήθηκε στις 6 Δεκεμβρίου 2016.
- ↑ «Time Slycat Web-based ensemble analysis and visualization platform» (στα Αγγλικά). Ανακτήθηκε στις 3 Οκτωβρίου 2017.
- ↑ «Python module for machine learning multivariate time series» (στα Αγγλικά). Ανακτήθηκε στις 14 Μαρτίου 2018.
Περαιτέρω μελέτη
[Επεξεργασία | επεξεργασία κώδικα]- Box, George; Jenkins, Gwilym (1976), Time Series Analysis: forecasting and control, rev. ed., Oakland, California: Holden-Day
- Cowpertwait PSP, Metcalfe AV (2009), Εισαγωγική χρονολογική σειρά με R, Springer .
- Durbin J., Koopman SJ (2001), Ανάλυση Χρονικών Σειρών από τις Κρατικές Διαστημικές Μέθοδοι, Oxford University Press .
- Gershenfeld, Neil (2000), The Nature of Mathematical Modeling, Cambridge University Press, ISBN 978-0-521-57095-4, OCLC 174825352
- Hamilton, James (1994), Time Series Analysis, Princeton University Press, ISBN 0-691-04289-6
- Priestley, ΜΒ (1981), Spectral Analysis and Time Series, Academic Press. (ISBN 978-0-12-564901-8) ISBN 978-0-12-564901-8
- Shasha, D. (2004), High Performance Discovery in Time Series, Springer, ISBN 0-387-00857-8
- Shumway RH, Stoffer (2011), Ανάλυση Χρονικών Σειρών και Εφαρμογές τους, Springer.
- Weigend AS, Gershenfeld NA (Eds.) (1994), Πρόβλεψη χρονοσειράς : Πρόβλεψη του μέλλοντος και κατανόηση του παρελθόντος. Πρακτικά του Προχωρημένου Ερευνητικού Εργαστηρίου του ΝΑΤΟ για τη συγκριτική ανάλυση χρονοσειρών (Santa Fe, Μάιος 1992), Addison-Wesley.
- Wiener, N. (1949), Εξαγωγή, παρεμβολή και εξομάλυνση σταθερής χρονοσειράς, MIT Press .
- Woodward, WA, Gray, HL & Elliott, AC (2012), Applied Time Series Analysis, CRC Press .
Εξωτερικοί σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]- Χρονολογικές σειρές στην Εγκυκλοπαίδεια Μαθηματικών.
- Ένα πρώτο μάθημα για την Ανάλυση Χρονικών Σειρών - Ένα βιβλίο ανοιχτού κώδικα για την ανάλυση χρονοσειρών με την SAS .
- Εισαγωγή στην Ανάλυση Χρονικών Σειρών (Εγχειρίδιο Στατιστικής Μηχανικής) - Ένας πρακτικός οδηγός για την Ανάλυση Χρονοσειρών.
- MATLAB Toolkit για τον υπολογισμό πολλαπλών μέτρων σε βάσεις δεδομένων χρονοσειρών.
- Ένα μάθημα Matlab για τα φάσματα ισχύος, wavelet ανάλυση, και συνοχή Αρχειοθετήθηκε 2018-11-07 στο Wayback Machine. στην ιστοσελίδα με πολλά άλλα μαθήματα.
- Έρευνα TimeViz
- Gaussian Διαδικασίες για Εκμάθηση Μηχανών: Ιστοσελίδα Βιβλίου
- Παρατήρηση εργασιών CRAN χρονοσειρών - Χρονική σειρά σε R
- Ανάλυση TimeSeries με Pandas
