Ολοκλήρωμα: Διαφορά μεταξύ των αναθεωρήσεων
Χωρίς σύνοψη επεξεργασίας |
|||
| Γραμμή 1: | Γραμμή 1: | ||
[[Αρχείο:Integral example.png|thumb|right|Το ολοκλήρωμα της συνάρτησης ''f''(''x'') από το ''a'' στο ''b'' είναι η επιφάνεια πάνω από τον άξονα ''x'' και κάτω από την καμπύλη ''y'' = ''f''(''x''), μείον την επιφάνεια κάτω από τον άξονα ''x'' και πάνω από την καμπύλη, για ''x'' στο διάστημα [''a'',''b''].]] |
[[Αρχείο:Integral example.png|thumb|right|Το ολοκλήρωμα της συνάρτησης ''f''(''x'') από το ''a'' στο ''b'' είναι η επιφάνεια πάνω από τον άξονα ''x'' και κάτω από την καμπύλη ''y'' = ''f''(''x''), μείον την επιφάνεια κάτω από τον άξονα ''x'' και πάνω από την καμπύλη, για ''x'' στο διάστημα [''a'',''b''].]] |
||
Η '''ολοκλήρωση''' είναι στοιχειώδης έννοια των προχωρημένων [[μαθηματικά|μαθηματικών]], ειδικά στα πεδία του [[απειροστικός λογισμός|απειροστικού λογισμού]] και της [[μαθηματική ανάλυση|μαθηματικής ανάλυσης]]. Έστω |
Η '''ολοκλήρωση''' είναι στοιχειώδης έννοια των προχωρημένων [[μαθηματικά|μαθηματικών]], ειδικά στα πεδία του [[απειροστικός λογισμός|απειροστικού λογισμού]] και της [[μαθηματική ανάλυση|μαθηματικής ανάλυσης]]. Έστω μια συνάρτηση f με ανεξάρτητη μεταβλητή την x. Έστω υποσύνολο D του πεδίου ορισμού της συνάρτησης. Έστω (μεταβλητή) ''[[διαμέριση]]'' P, n στοιχείων, του συνόλου D, με ''λεπτότητα'' ||P||. Με απλά λόγια διαμέριση λέγεται οποιοσδήποτε τρόπος κομματιάζει το D σε n κομμάτια, ενώ η λεπτότητά δείχνει πόσο μεγάλο είναι το μεγαλύτερο κομμάτι της διαμέρισης. Ένα κομμάτι της διαμέρισης συμβολίζεται με [[διαφορικό|δx]]. Σε κάθε στοιχείο δx<sub>i</sub> της διαμέρισης (δηλαδή σε κάθε κομμάτι) επιλέγεται ένα σημείο x<sub>i</sub> και υπολογίζεται η f(x<sub>i</sub>). Έστω το άθροισμα: |
||
<math>\sum_{i=1}^{n} f(x_i)\delta x_i</math> |
<math>\sum_{i=1}^{n} f(x_i)\delta x_i</math> |
||
Έκδοση από την 10:00, 31 Μαΐου 2011
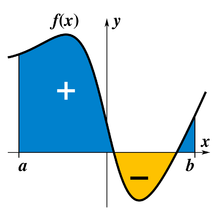
Η ολοκλήρωση είναι στοιχειώδης έννοια των προχωρημένων μαθηματικών, ειδικά στα πεδία του απειροστικού λογισμού και της μαθηματικής ανάλυσης. Έστω μια συνάρτηση f με ανεξάρτητη μεταβλητή την x. Έστω υποσύνολο D του πεδίου ορισμού της συνάρτησης. Έστω (μεταβλητή) διαμέριση P, n στοιχείων, του συνόλου D, με λεπτότητα ||P||. Με απλά λόγια διαμέριση λέγεται οποιοσδήποτε τρόπος κομματιάζει το D σε n κομμάτια, ενώ η λεπτότητά δείχνει πόσο μεγάλο είναι το μεγαλύτερο κομμάτι της διαμέρισης. Ένα κομμάτι της διαμέρισης συμβολίζεται με δx. Σε κάθε στοιχείο δxi της διαμέρισης (δηλαδή σε κάθε κομμάτι) επιλέγεται ένα σημείο xi και υπολογίζεται η f(xi). Έστω το άθροισμα:
Τότε ως ορισμένο ολοκλήρωμα της f στο D ορίζεται το όριο (αν υπάρχει):
Ο ορισμένο ολοκλήρωμα συμβολίζεται με , δηλαδή ισχύει:
Σημειώνεται ότι ισχύει:
Στην περίπτωση που το D είναι διάστημα με άκρα τα a,b (a μεγαλύτερο ή ίσο του b) το ολοκλήρωμα συμβολίζεται με:
Ο όρος "ολοκλήρωμα" μπορεί επίσης να αναφέρεται στην έννοια της αντιπαραγώγου ή παράγουσας συνάρτησης, η οποία είναι μια συνάρτηση F της οποίας η παράγωγος είναι η αρχική f. Σ' αυτή την περίπτωση λέγεται και αόριστο ολοκλήρωμα, ενώ τα ολοκληρώματα που αναφέρονται σε αυτό το άρθρο λέγονται ορισμένα ολοκληρώματα. Τα αόριστα ολοκληρώματα δεν αναφέρονται σε κάποιο συγκεκριμένο υποσύνολο του πεδίου ορισμού, άρα δεν προσδιορίζουμε που ολοκληρώνουμε, ενώ κατά τα άλλα ο συμβολισμός παραμένει ο ίδιος. Ο λόγος για αυτό είναι οι σχέσεις:
όπου ci οποιαδήποτε πραγματική σταθερά
Με άλλα λόγια το ολοκλήρωμα της παραγώγου ισούται (με μία διαφορά) με την αρχική συνάρτηση. Άρα για να βρούμε την αντιπαράγωγο μιας συνάρτησης, αρκεί να υπολογίσουμε το ολοκλήρωμά της.
Μερικοί συγγραφείς θεωρούν διαφορετική την έννοια της αντιπαραγώγου από το αόριστο ολοκλήρωμα. Η διαφορά είναι ότι αντιπαράγωγος είναι κάθε συνάρτηση της οποίας η παράγωγος δίνει την f, ενώ το αόριστο ολοκλήρωμα της f είναι μια οικογένεια συναρτήσεων που διαφέρουν μεταξύ τους κατά μια σταθερά, κάθε μια από τις οποίες είναι αντιπαράγωγος της f.[1]
Ιστορική αναδρομή
Οι αρχές της ολοκλήρωσης διατυπώθηκαν από τον Ισαάκ Νεύτονα και τον Γκότφριντ Βίλχελμ Λάιμπνιτς στο τέλος του 17ου αιώνα. Μέσα από το θεμελιώδες θεώρημα του απειροστικού λογισμού, που ανέπτυξαν ανεξάρτητα, η ολοκλήρωση συνδέεται με την παραγώγιση και το ορισμένο ολοκλήρωμα μιας συνάρτησης μπορεί εύκολα να υπολογιστεί μόλις γίνει γνωστή η αντιπαράγωγος. Τα ολοκληρώματα και οι παράγωγοι έγιναν τα βασικά εργαλεία του απειροστικού λογισμού, με πολυάριθμες εφαρμογές στην επιστήμη και τη μηχανική.
Ένας αυστηρός μαθηματικός ορισμός του ολοκληρώματος δόθηκε από τον Μπέρναρντ Ρίμαν. Βασίζεται σε ένα όριο που προσεγγίζει την επιφάνεια μιας καμπυλόγραμμης περιοχής με το να σπάει την περιοχή σε κάθετες λωρίδες. Τον 19ο αιώνα άρχισαν να εμφανίζονται πιο εξελιγμένες έννοιες του ολοκληρώματος, όπου ο τύπος της συνάρτησης όπως και το πεδίο ορισμού της ολοκλήρωσης έχουν γενικευθεί. Το επικαμπύλιο ολοκλήρωμα ορίζεται για συναρτήσεις δύο ή τριών μεταβλητών, και το διάστημα της ολοκλήρωσης [a,b] αντικαθίστανται από μια καμπύλη μεταξύ δυο σημείων του επιπέδου ή του χώρου. Στο επιφανειακό ολοκλήρωμα, η καμπύλη αυτή αντικαθίσταται από μια επιφάνεια στον τρισδιάστατο χώρο. Τα ολοκληρώματα διαφορικής μορφής παίζουν θεμελιώδη ρόλο στη σύγχρονη διαφορική γεωμετρία. Αυτές οι γενικεύσεις του ολοκληρώματος αρχικά εξελίχθηκαν από τις ανάγκες της φυσικής, και παίζουν σημαντικό ρόλο στη διατύπωση πολλών φυσικών νόμων, κυρίως αυτών της ηλεκτροδυναμικής. Σύγχρονες έννοιες της ολοκλήρωσης βασίζονται στην αφηρημένη μαθηματική θεωρία γνωστή ως ολοκλήρωση Λεμπέγκ, που αναπτύχθηκε από τον Ανρί Λεμπέγκ.
Θεμελιώδες θεώρημα του απειροστικού λογισμού
Το θεμελιώδες θεώρημα του απειροστικού λογισμού δηλώνει ότι η ολοκλήρωση και η παραγώγιση είναι αντίστροφες πράξεις.
Έστω f μια πραγματική συνεχής συνάρτηση που ορίζεται σε κλειστό διάστημα, . Η συνάρτηση με
είναι συνεχής και ισχύει
- για κάθε
Η F ονομάζεται αρχική ή αντιπαράγωγος της f.
Έστω f μια πραγματική συνεχής συνάρτηση που ορίζεται σε κλειστό διάστημα, και F η αρχική της f. Τότε ισχύει
Ολοκληρώματα Νταρμπού και Ρίμαν

Σε ένα κλειστό διάστημα ορίζουμε μια διαμέριση . Προσεγγίζουμε το εμβαδό που περικλείεται από το γράφημα της f και τον άξονα x με αθροίσματα εμβαδών ορθογωνίων
Τα αθροίσματα αυτά ονομάζονται αθροίσματα Ρίμαν. Στην ειδική περίπτωση που θεωρούμε τα μέγιστα δυνατά εμβαδά ορθογωνίων
το αθροίσμα ονομάζενται άνω αθροίσμα Νταρμπού. Στην περίπτωση που θεωρούμε τα ελάχιστα δυνατά εμβαδά ορθογωνίων
το αθροίσματα ονομάζεται κάτω αθροίσμα Νταρμπού.
Θεωρούμε εκλεπτύνσεις της αρχικής διαμέρισης, δηλαδή λεπτότερες διαμερίσεις. Μια συνάρτηση είναι ολοκληρώσιμη κατά Ρίμαν, αν τα αθροίσματα Ρίμαν συγκλίνουν καθώς ο αριθμός διαστημάτων διαμέρισης τίνει στο άπειρο. Μια συνάρτηση είναι ολοκληρώσιμη κατά Νταρμπού, αν τα άνω και κάτω αθροίσματα Νταρμπού συγκλίνουν στην ίδια τιμή.
Τα ολοκληρώματα Νταρμπού και Ρίμαν είναι ισοδύναμα.
Ολοκλήρωμα Λεμπέγκ

Το ολολήρωμα Λεμπέγκ βασίζεται στην θεωρία μέτρου. Χρησημοποιεί το μέτρο Λεμπέγκ, που γενικεύει την έννοια του μήκους.
Αρχικά ολοκληρώνουμε μια απλή συνάρτηση f, δηλαδή μια συνάρτηση με πεπερασμένο πλήθος τιμών, έστω . Θεωρούμε τα υποσύνολα του πεδίου ορισμού . Το μέτρο μ() αυτών των συνόλων αντιστοιχεί στο μήκος τους. Τότε το ολοκλήρωμα Λεμπέγκ ορίζεται ως
Για να βρούμε το ολοκλήρωμα μιας συνεχούς συνάρτησης την προσεγγίζουμε με απλές συναρτήσεις.
Το ολοκλήρωμα Λεμπέγκ αποτελεί γενίκευση του ολοκληρώματος Ρίμαν. Μια συνάρτηση ολοκληρώσιμη κατά Ρίμαν είναι ολοκληρώσιμη κατά Λεμπέγκ και τα δυο ολοκληρώματα έχουν την ίδια τιμή. Αντιστρόφως μια συνάρτηση ολοκληρώσιμη κατά Λεμπέγκ δεν είναι απαραίτητα ολοκληρώσιμη κατά Ρίμαν.
Είδη και πολλαπλότητα ολοκληρωμάτων
Ένα ολοκλήρωμα εκτός από απλό μπορεί να είναι διπλό ή τριπλό και γενικά πολλαπλό. Η πολλαπλότητα ενός ολοκληρώματος δηλώνει τον αριθμό των μεταβλητών ως προς τις οποίες γίνεται η ολοκλήρωση, δηλαδή τα ορίσματα της συνάρτησης που ολοκληρώνεται. Τα είδη των ολοκληρωμάτων δηλώνουν αντίστοιχα τη φύση του αποτελέσματος του ολοκληρώματος. Το ολοκλήρωμα α' είδους αντιστοιχεί γεωμετρικά σε γραμμή, του δεύτερου είδους σε επιφάνεια, του τρίτου είδους σε όγκο και ούτω κάθ' εξής.
Παραπομπές
- ↑ Θεοδούλα Ν. Γράψα. «Το Αόριστο Ολοκλήρωμα» (doc). Βοηθητικό υλικό Ελληνικού Ανοικτού Πανεπιστημίου. Ανακτήθηκε στις 05-10-2008. Ελέγξτε τις τιμές ημερομηνίας στο:
|accessdate=(βοήθεια)
| Αυτό το μαθηματικό λήμμα χρειάζεται επέκταση. Μπορείτε να βοηθήσετε την Βικιπαίδεια επεκτείνοντάς το. |
| Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα integral της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 4.0. (ιστορικό/συντάκτες). |









![{\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ccf6eb823414cc4f75e408522881f3423c52534d)
![{\displaystyle F\colon [a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/68ce18ea6666c32276447809d9ec4db1f1b29137)


![{\displaystyle x\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/026357b404ee584c475579fb2302a4e9881b8cce)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle \sum _{k=1}^{n}f(t_{k})(x_{k}-x_{k-1}),\quad t_{k}\in [x_{k-1},x_{k}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/528cc7ffd8e0f751835939af998ae63bc982586b)





