Εξίσωση θερμότητας

Στο παραπάνω παράδειγμα, η εξίσωση θερμότητας δυο διαστάσεων προβλέπει ότι αν μια περιοχή ,μιας κατά τα άλλα ψυχρής μεταλλικής πλάκας θερμανθεί ,τότε καθώς μεταβάλλεται ο χρόνος, η θερμοκρασία της περιοχής αυτής σταδιακά θα μειώνεται, αρχίζοντας από τις άκρες της περιοχής και συνεχίζοντας στο εσωτερικό της. Παράλληλα το τμήμα της πλάκας έξω απ' αυτήν την περιοχή θ' αρχίσει να θερμαίνεται. Τελικά ,ολόκληρη η πλάκα θα φτάσει σε μια ομοιόμορφη μέση θερμοκρασία. Στην απεικόνιση αυτή ,αμφότερα το ύψος και το χρώμα υποδηλώνουν θερμοκρασία.

Η εξίσωση θερμότητας είναι παραβολική διαφορική εξίσωση μερικών παραγώγων ,η οποία περιγράφει την κατανομή της θερμότητας (ή την μεταβολή της θερμοκρασίας) σε μια δοσμένη περιοχή καθώς μεταβάλλεται ο χρόνος.

Διατύπωση της εξίσωσης

Για μια συνάρτηση u(x,y,z,t) τριών χωρικών μεταβλητών (x,y,z) (βλ. καρτεσιανές συντεταγμένες) και μιας μεταβλητής χρόνου t, η εξίσωση της θερμότητας είναι

${\frac {\partial u}{\partial t}}-\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}+{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}\right)=0$

Πιο γενικά σε οποιοδήποτε σύστημα συντεταγμένων:

${\frac {\partial u}{\partial t}}-\alpha \nabla ^{2}u=0$

όπου α είναι μια θετική σταθερά, και το Δ ή ∇² συμβολίζει τον τελεστή Λαπλάς. Στο φυσικό πρόβλημα της μεταβολής της θερμοκρασίας,η συνάρτηση u(x,y,z,t) δίνει την θερμοκρασία ενώ η α είναι η θερμική διαχυτικότητα. Για τη μαθηματική μελέτη του προβλήματος είναι επαρκές να θεωρήσουμε την περίπτωση α = 1.

Παρατηρήστε ότι η εξίσωση της θερμότητας ,η οποία δίνεται από τον πρώτο θερμοδυναμικό νόμο (δηλαδή η αρχή διατήρησης της ενέργειας), μπορεί να γραφεί στην ακόλουθη μορφή (με την υπόθεση ότι δεν υπάρχει κάποια μεταφορά μάζας ή εκπομπή ακτινοβολίας). Αυτή η μορφή της εξίσωσης είναι πιο γενική και ιδιαίτερα χρήσιμη στην αναγνώριση της επιρροή της κάθε ιδιότητας στον κάθε όρο. π.χ c_p ή $\rho$

$\rho c_{p}{\frac {\partial T}{\partial t}}-\nabla \cdot \left(k\nabla T\right)={\dot {q}}_{V}$

όπου ${\dot {q}}_{V}$ είναι η ογκομετρική θερμική ροή.

Η εξίσωση της θερμότητας έχει θεμελιώδη αξία σε διάφορα επιστημονικά πεδία. Στα μαθηματικά, είναι το αρχέτυπο των παραβολικών διαφορικών εξισώσεων με μερικές παραγώγους. Στη Θεωρία πιθανοτήτων, η εξίσωση της θερμότητας σχετίζεται με την μελέτη της κίνησης Brown μέσω της εξίσωσης Fokker–Planck. Στα οικονομικά μαθηματικά χρησιμοποιείται για τη λύση της διαφορικής εξίσωσης μερικών παραγώγων Black–Scholes. Η εξίσωση διάχυσης, μια πιο γενική μορφή της εξίσωσης της θερμότητας, έρχεται σε σύνδεση με τη μελέτη της χημικής διάχυσης και άλλων σχετικών διεργασιών.

Γενική Περιγραφή

Λύση μιας μονοδιάστατης εξίσωσης θερμότητας. Η θερμοκρασία (u) είναι αρχικά κατανεμημένη σε ένα μονοδιάστατο ,μήκους 1 διάστημα (x = [0,1]) ,όπου τα ακραία σημεία είναι μονωμένα. Η κατανομή της θερμοκρασίας προσεγγίζει την ισορροπία με την πάροδο του χρόνου.

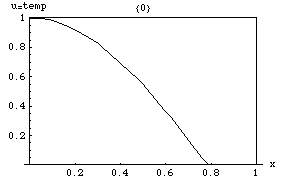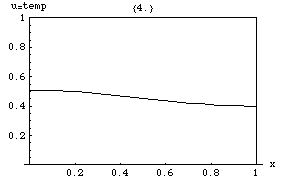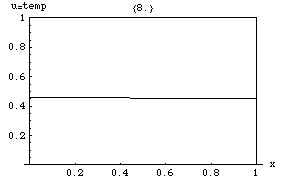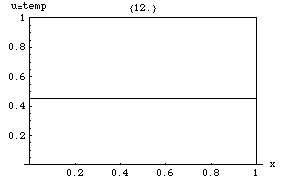
Ας υποθέσουμε ότι έχουμε μια συνάρτηση u η οποία περιγράφει την θερμοκρασία σε ένα δοσμένο σημείο (x, y, z). Η τιμή της συνάρτησης u μεταβάλλεται με την πάροδο του χρόνου καθώς η θερμότητα διαδίδεται στον χώρο. Η εξίσωση θερμότητας χρησιμοποιείται για να προσδιορίσουμε την μεταβολή της συνάρτησης u με το χρόνο. Ο ρυθμός μεταβολή της u είναι ανάλογος με την "καμπυλότητα" της u.

Στο διπλανό σχήμα περιγράφεται ο τρόπος με τον οποίο μεταβάλλεται η θερμότητα σε μια μεταλλική ράβδο με την πάροδο του χρόνου. Μια από τις ενδιαφέρουσες ιδιότητες της εξίσωσης θερμότητας είναι η αρχή του μεγίστου η οποία λέει ότι η μέγιστη τιμή της u

Άλλη μια ενδιαφέρουσα ιδιότητα είναι ότι ενώ η u έχει ασυνέχεια σε ένα αρχικό (χρονικό) σημείο t = t₀, η θερμοκρασία εξομαλύνεται καθώς t > t₀. Παραδείγματος χάρη ,αν μια μεταλλική ράβδος έχει θερμοκρασία 0 και μια άλλη θερμοκρασία 100 και τις φέρουμε σε επαφή άκρο με άκρο, τότε πολύ γρήγορα η θερμοκρασία στο σημείο επαφής θα φτάσει τους 50 και η γραφική παράσταση της θερμοκρασίας θα διαπεράσει ομαλά τις τιμές από το 0 έως το 100.

Η εξίσωση θερμότητας χρησιμοποιείται στην θεωρία πιθανοτήτων για να περιγράψει τον τυχαίο περίπατο. Για το λόγο αυτό έχει εφαρμογή στα οικονομικά μαθηματικά.

Είναι επίσης σημαντική στη γεωμετρία Riemann και συνακόλουθα στη τοπολογία: προσαρμόστηκε (η εξίσωση θερμότητας) από τον Richard Hamilton όταν όρισε τη Ricci flow η οποία χρησιμοποιήθηκε αργότερα από τον Γκριγκόρι Πέρελμαν για να αποδείξει την τοπολογική εικασία του Πουανκαρέ.

Το φυσικό πρόβλημα και η εξίσωση

Παραγώγιση σε μια διάσταση

Η εξίσωση θερμότητας προέρχεται από το νόμο του Φουριέ και από την αρχή διατήρησης της ενέργειας. Σύμφωνα με το νόμο του Φουριέ, ο ρυθμός ροής θερμικής ενέργειας ανά μονάδα επιφάνειας μέσω μιας επιφάνειας είναι ανάλογος με την αρνητική βαθμίδα θερμοκρασίας κατά μήκος της επιφάνειας ,

$\mathbf {q} =-k\,\nabla u\$

όπου k είναι η θερμική αγωγιμότητα και u είναι η θερμοκρασία. Σε μία διάσταση, η βαθμίδα θερμοκρασίας είναι μια συνήθης χωρική παράγωγος, κι έτσι ο νόμος του Φουριέ θα είναι:

$q=-k{\frac {\partial u}{\partial x}}\,$

Απουσία παραγωγής έργου, η μεταβολή της εσωτερικής ενέργειας ανά μονάδα όγκου στο υλικό , ΔQ, είναι ανάλογη με την μεταβολή της θερμοκρασίας, Δu (σε αυτό το τμήμα και μόνο, με Δ θα συμβολίζουμε τη διαφορά και όχι τον τελεστή Λαπλάς). Δηλαδή,

$\Delta Q=c_{p}\rho \,\Delta u\,$

όπου c_p είναι η θερμοχωρητικότητα και ρ η πυκνότητα μάζας του υλικού. Θέτοντας την ενέργεια μηδέν στην απόλυτη μηδενική θερμοκρασία, η προηγούμενη εξίσωση μπορεί να γραφεί ως εξής

$Q=c_{p}\rho u.\,$

Η αύξηση εσωτερικής ενέργειας σε μια μικρή χωρική περιοχή του υλικού

$x-\Delta x\leq \xi \leq x+\Delta x$

κατά τη διάρκεια της χρονικής περιόδου

$t-\Delta t\leq \tau \leq t+\Delta t$

δίνεται από

$c_{p}\rho \int _{x-\Delta x}^{x+\Delta x}[u(\xi ,t+\Delta t)-u(\xi ,t-\Delta t)]\,d\xi =c_{p}\rho \int _{t-\Delta t}^{t+\Delta t}\int _{x-\Delta x}^{x+\Delta x}{\frac {\partial u}{\partial \tau }}\,d\xi \,d\tau$

όπου χρησιμοποιήσαμε το θεμελιώδες θεώρημα του λογισμού. Απουσία παραγωγής έργου και αν δεν υπάρχουν πηγές θερμότητας ούτε καταβόθρες, η μεταβολή εσωτερικής ενέργειας στο διάστημα [x−Δx, x+Δx] αντιπρoσωπεύεται εξ ολοκλήρου από τη ροή θερμότητας κατά μήκος του συνόρου της επιφάνειας. Από το νόμο του Φουριέ ,αυτό σημαίνει

$k\int _{t-\Delta t}^{t+\Delta t}\left[{\frac {\partial u}{\partial x}}(x+\Delta x,\tau )-{\frac {\partial u}{\partial x}}(x-\Delta x,\tau )\right]\,d\tau =k\int _{t-\Delta t}^{t+\Delta t}\int _{x-\Delta x}^{x+\Delta x}{\frac {\partial ^{2}u}{\partial \xi ^{2}}}\,d\xi \,d\tau$

λόγω και πάλι του θεμελιώδους θεωρήματος του λογισμού. Λόγω τώρα της αρχής διατήρησης της ενέργειας θα έχουμε,

$\int _{t-\Delta t}^{t+\Delta t}\int _{x-\Delta x}^{x+\Delta x}[c_{p}\rho u_{\tau }-ku_{\xi \xi }]\,d\xi \,d\tau =0.$

Το οποίο αληθεύει για οποιοδήποτε ορθογώνιο [t −Δt, t + Δt] × [x − Δx, x + Δx]. Λόγω του θεμελιώδους λήμματος του λογισμού των μεταβολών , οι ολοκληρωτέες θα πρέπει να μηδενιστούν ταυτοτικά:

$c_{p}\rho u_{t}-ku_{xx}=0.\,\!$

Η οποία μπορεί να ξαναγραφεί ως εξής:

$u_{t}={\frac {k}{c_{p}\rho }}u_{xx},$

ή:

${\frac {\partial u}{\partial t}}={\frac {k}{c_{p}\rho }}\left({\frac {\partial ^{2}u}{\partial x^{2}}}\right)$

Η οποία είναι η εξίσωση θερμότητας, όπου ο συντελεστής (που συνήθως συμβολίζεται με α)

$\alpha ={\frac {k}{c_{p}\rho }}\,\!$

ονομάζεται θερμικη διαχυτικοτητα.

Ένας πρόσθετος όρος που μπορεί να εισαχθεί στη εξίσωση για να λογαριάσουμε την απώλεια θερμότητας λόγω εκπομπής ακτινοβολίας , ο οποίος εξαρτάται από την υπερβολική θερμοκρασία u = T − T_s σε ένα δοσμένο σημείο συγκρινόμενη με την θερμοκρασία του περιβάλλοντος χώρου. Σε υπερβολικά χαμηλές θερμοκρασίες , η απώλεια θερμότητας είναι περίπου μu, δίνοντας μια μονοδιάστατη εξίσωση μεταφοράς θερμότητας της μορφής

${\frac {\partial u}{\partial t}}={\frac {k}{c_{p}\rho }}\left({\frac {\partial ^{2}u}{\partial x^{2}}}\right)-\mu u.$

Σε υπερβολικά υψηλές θερμοκρασίες, ωστόσο, ο νόμος Στέφαν-Μπόλτζμαν δίνει μια καθαρή απώλεια θερμότητας λόγω ακτινοβολίας ,η οποία είναι ανάλογη προς το $T^{4}-T_{s}^{4}$, και η παραπάνω εξίσωση είναι ανακριβής. Για μεγάλες θερμοκρασίες έχουμε, $T^{4}-T_{s}^{4}\approx u^{4}$, το οποίο δίνει μια εξίσωση μεταφοράς θερμότητας υψηλής θερμοκρασίας της μορφής

${\frac {\partial u}{\partial t}}=\alpha \left({\frac {\partial ^{2}u}{\partial x^{2}}}\right)-\ mu^{4}$

όπου $\ m=\epsilon \sigma p/\rho Ac_{p}$. Εδώ, σ είναι η σταθερά Στέφαν-Μπόλτζμαν, ε είναι η χαρακτηριστική σταθερά του υλικού, p είναι η περίμετρος διατομής της ράβδου και A είναι το εμβαδόν της εγκάρσιας διατομής. Ωστόσο, χρησιμοποιώντας T αντί για u παίρνουμε μια καλύτερη προσέγγιση στην περίπτωση αυτή.

Το πρόβλημα στις τρεις διαστάσεις

Στις ειδικές περιπτώσεις της κυματικής διάδοσης της θερμότητας σ' ένα ισότροπο και ομογενές μέσο σ' έναν 3-διάστατο χώρο , αυτή η εξίσωση είναι

${\partial u \over \partial t}=\alpha \left({\partial ^{2}u \over \partial x^{2}}+{\partial ^{2}u \over \partial y^{2}}+{\partial ^{2}u \over \partial z^{2}}\right)$ $=\alpha (u_{xx}+u_{yy}+u_{zz})\quad$

όπου:

• u = u(x, y, z, t) είναι η θερμοκρασία ως συνάρτηση χώρου και χρόνου·
• ${\frac {\partial u}{\partial t}}$ είναι ο ρυθμός μεταβολής της θερμοκρασίας σ' ένα σημείο με την πάροδο του χρόνου·
• u_xx, u_yy, and u_zz είναι οι δεύτερες χωρικές παράγωγοι (thermal conductions) της θερμοκρασίας στις κατευθύνσεις x, y, και z αντίστοιχα·
• $\alpha ={\frac {k}{c_{p}\rho }}$ είναι η θερμική διαχυτικότητα, μια χαρακτηριστική ιδιότητα του υλικού που εξαρτάται από την θερμική αγωγιμότητα k, την πυκνότητα μάζας ρ, και την ειδική θερμοχωρητικότητα c_p.

Η εξίσωση θερμότητα είναι συνέπεια του νόμου του Φουριέ για την αγωγιμότητα (βλέπε θερμική αγωγιμότητα).

Στην περίπτωση που το μέσο δεν είναι ολόκληρος ο χώρος, πρέπει να ορίσουμε συνοριακές συνθήκες για την u ώστε να έχουμε μονοσήμαντη λύση της εξίσωσης θερμότητας.

Εσωτερική παραγωγή θερμότητας

Η παραπάνω συνάρτηση u αναπαριστά την θερμοκρασία ενός σώματος. Εναλλακτικά, είναι ορισμένες φορές βολικό να αλλάξουμε τις μονάδες μέτρησης και να αναπαραστήσουμε την u ως την θερμική ροή ενός μέσου. Και από την στιγμή που η θερμική ροή είναι ανάλογη με την θερμοκρασία σε ένα ομογενές μέσο, η εξίσωση θερμότητας έχει ισχύ και στις νέες μονάδες μέτρησης.

Ας υποθέσουμε ότι ένα σώμα υπακούει στην εξίσωση θερμότητας και, επιπλέον παράγει την δικιά του θερμότητα ανά μονάδα όγκου (π.χ., σε watts/litre - W/L) σε ένα ρυθμό που δίνεται από μια γνωστή συνάρτηση q που ποικίλει ανάλογα με τον χώρο και τον χρόνο. Τότε η θερμότητα ανά μονάδα όγκου u ικανοποιεί μια εξίσωση της μορφής

${\frac {\partial u}{\partial t}}=\alpha \left({\partial ^{2}u \over \partial x^{2}}+{\partial ^{2}u \over \partial y^{2}}+{\partial ^{2}u \over \partial z^{2}}\right)+{\frac {1}{c_{p}\rho }}q.$

Για παράδειγμα ,το νήμα πυράκτωσης ενός λαμπτήρα βολφραμίου παράγει θερμότητα, έτσι θα έχει μη μηδενική τιμή για την q όταν είναι αναμμένος. Ενώ όταν ο λαμπτήρας είναι απενεργοποιημένος, η τιμή της q για τον νήμα πυράκτωσης θα είναι μηδέν.

Επίλυση της εξίσωσης θερμότητας χρησιμοποιώντας σειρές Fourier

Εξιδανικευμένη διάταξη φυσικής για την θερμική αγωγιμότητα σε μια ράβδο με ομογενείς συνοριακές συνθήκες.

Η ακόλουθη τεχνική λύσης για την εξίσωση θερμότητας προτάθηκε από τον Ζοζέφ Φουριέ στην πραγματεία του Théorie analytique de la chaleur (Αναλυτική θεωρία της θερμότητας), η οποία δημοσιεύτηκε το 1822. Ας θερωρήσουμε την εξίσωση θερμότητας για μια χωρική μεταβλητή. Η οποία μπορεί να προσομοιώσει την θερμική αγωγιμότητα σε μία ράβδο. Η εξίσωση είναι

()

όπου η u = u(x, t) είναι μια συνάρτηση δύο μεταβλητών x και t. Εδώ

• x είναι η χωρική μεταβλητή, έτσι x ∈ [0, L], όπου L είναι το μήκος της ράβδου.
• t είναι η μεταβλήτη χρόνου, έτσι t ≥ 0.

Υποθέτουμε την αρχική συνθήκη

$u(x,0)=f(x)\quad \forall x\in [0,L]$

(EqNote)

όπου η συνάρτηση f είναι δοσμένη, και τις συνοριακές συνθήκες

$u(0,t)=0=u(L,t)\quad \forall t>0$.

(Πρότυπο:EqRef)

Ας επιχειρήσουμε να βρούμε μια λύση της Πρότυπο:EqNote που να μην είναι ταυτοτικά μηδέν , να ικανοποιεί της συνοριακές συνθήκες Πρότυπο:EqNote και να έχει την παρακάτω ιδιότητα:η u είναι ένα γινόμενο στο οποίο στο οποίο η εξάρτηση της u από τις x, t χωρίζεται, δηλαδή:

$\displaystyle u(x,t)=X(x)T(t).$

(Πρότυπο:EqRef)

Αυτή η τεχνική λύσης ονομάζεται χωριζομένων μεταβλητών. Αντικαθιστώντας την u πίσω στην εξίσωση Πρότυπο:EqNote έχουμε,

${\frac {T'(t)}{\alpha T(t)}}={\frac {X''(x)}{X(x)}}.$

Και από την στιγμή που το δεξί μέλος εξαρτάται μόνο από το x και το αριστερό μόνο από το t, τα δύο μέλη θα είναι ίσα με μια σταθερή ποσότητα −λ. Κι έτσι:

$T'(t)=-\lambda \alpha T(t)$

(Πρότυπο:EqRef)

και

$X''(x)=-\lambda X(x).$

(Πρότυπο:EqRef)

Θα δείξουμε τώρα ότι δεν υπάρχουν μη τετριμμένες λύσεις για την Πρότυπο:EqNote για λ ≤ 0 δεν υπάρχουν:

1. Για λ < 0, υπάρχουν πραγματικοί αριθμοί B, C τέτοιοι ώστε

   $X(x)=Be^{{\sqrt {-\lambda }}\,x}+Ce^{-{\sqrt {-\lambda }}\,x}.$

   Λόγω τον αρχικών συνθηκών πρέπει Χ(0) = Χ(L) = 0 και έτσι προκύπτει ότι Β = C = 0
2. Για λ = 0. Υπάρχουν B, C τέτοιοι ώστε X(x) = Bx + C. Με την ίδια διαδικασία όπως την 1 καταλήγουμε ότι B = C = 0
3. Για λ > 0. υπάρχουν A, B, C τέτοιοι ώστε

   $T(t)=Ae^{-\lambda \alpha t}$

   and

   $X(x)=B\sin({\sqrt {\lambda }}\,x)+C\cos({\sqrt {\lambda }}\,x).$

   Από τις αρχικές συνθήκες έχουμε ότι C = 0 και για κάποιο θετικό ακέραιο "'n, ισχύει ότι

   ${\sqrt {\lambda }}=n{\frac {\pi }{L}}.$

Έτσι λύνεται η εξίσωση θερμότητας στην ειδική περίπτωση όπου η εξάρτηση τηf u έχει την ειδική μορφή Πρότυπο:EqNote. Γενικά, το σύνολο των λύσεων της Πρότυπο:EqNote που ικανοποιούν τις συνοριακές συνθήκες Πρότυπο:EqNote ικανοποιεί επίσης την Πρότυπο:EqNote και την Πρότυπο:EqNote. Μπορούμε να δείξουμε ότι η λύση της Πρότυπο:EqNote, Πρότυπο:EqNote και της Πρότυπο:EqNote δίνεται από την

$u(x,t)=\sum _{n=1}^{\infty }D_{n}\sin \left({\frac {n\pi x}{L}}\right)e^{-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}$

όπου

$D_{n}={\frac {2}{L}}\int _{0}^{L}f(x)\sin \left({\frac {n\pi x}{L}}\right)\,dx.$

Υπάρχουν και άλλες λύσεις κλειστής μορφής.

Γενικεύοντας την τεχνική λύσης

Η τεχνική λύσης που χρησιμοποιήσαμε παραπάνω μπορεί κάλλιστα να επεκταθεί σε πολλές άλλου είδους εξισώσεις. Η ιδέα είναι ότι ο τελεστής u_xx με τις μηδενικές συνοριακές συνθήκες μπορεί να παρασταθεί σε όρους των ιδιοδιανυσμάτων του . Αυτό οδηγεί με φυσικό τρόπο σε μια βασική ιδέα της φασματικής θεωρίας ,αυτή των γραμμικών αυτοσυζυγών ή αυτοπροσαρτημένων τελεστών.

Θεωρήστε τον γραμμικό τελεστή Δu = u_xx. Η άπειρη ακολουθία συναρτήσεων

$e_{n}(x)={\sqrt {\frac {2}{L}}}\sin \left({\frac {n\pi x}{L}}\right)$

για n ≥ 1 είναι τα ιδιοδιανύσματα της Δ. Πράγματι

$\Delta e_{n}=-{\frac {n^{2}\pi ^{2}}{L^{2}}}e_{n}.$

Επιπλέον, οποιοδήποτε ιδιοδιάνυσμα f της Δ με τις συνοριακές συνθήκες f(0) = f(L) = 0 είναι της μορφής e_n για κάποιο n ≥ 1. Οι συναρτήσεις e_n για n ≥ 1 σχηματίζουν μια ορθοκανονική ακολουθία ως προς ένα συγκεκριμένο εσωτερικό γινόμενο στον χώρο των πραγματικών συναρτήσεων στο διάστημα [0, L]. Αυτό σημαίνει

$\langle e_{n},e_{m}\rangle =\int _{0}^{L}e_{n}(x)e_{m}^{*}(x)dx=\delta _{mn}$

Τελικά, η ακολουθία {e_n}_{n ∈ N} παράγει έναν πυκνό υπόχωρο του L²((0, L)). Αυτό δείχνει στην πράξη ότι έχουμε διαγωνοποιήσει τον τελεστή Δ.

Θερμική αγωγή σε μη ομογενή ανισότροπα μέσα

Γενικά, η μελέτη της θερμικής αγωγιμότητας βασίζεται σε ορισμένες αρχές. Η θερμική ροή είναι μια μορφή ενεργειακής ροής, και συνεπώς έχει νόημα να μιλήσουμε για τoν χρονικό ρυθμό ροής θερμότητας σε μια περιοχή του χώρου.

• Ο χρονικός ρυθμός θερμικής ροής προς μια περιοχή V δίνεται από μια εξαρτώμενη απ' τον χρόνο ποσότητα q_t(V). Υποθέτουμε ότι η q έχει μια πυκνότητα $Q$, έτσι ώστε

$q_{t}(V)=\int _{V}Q(x,t)\,dx\quad$

• Η θερμική ροή είναι μια εξαρτώμενη απ' τον χρόνο διανυσματική συνάρτηση H(x) η οποία έχει τα ακόλουθα χαρακτηριστικά: ο χρονικός ρυθμός της θερμικής ροής μέσω ενός απειροστού τμήματος μιας επιφάνεια με εμβαδόν dS και με το κανονικό μοναδιαίο διάνυσμα n είναι

$\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS$

Συνεπώς ο ρυθμός ροής της θερμότητας προς την περιοχή V δίνεται επίσης απ' το επιεπιφάνειο ολοκλήρωμα

$q_{t}(V)=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS$

όπου n(x) είναι το μοναδιαίο διάνυσμα στο σημείο x στραμμένο προς τα έξω.

• Ο νόμος του Φουριέ δηλώνει ότι η ροή θερμικής ενέργειας έχει την ακόλουθη γραμμική εξάρτηση από την βαθμίδα θερμοκρασίας

$\mathbf {H} (x)=-\mathbf {A} (x)\cdot \nabla u(x)$

όπου A(x) είναι ένας 3 × 3 πραγματικός πίνακας που είναι συμμετρικός θετικά ορισμένος.

• Από το θεώρημα απόκλισης (βλ. θεώρημα Gauss-Ostrogradsky), το προηγούμενο επιεπιφάνειο ολοκλήρωμα για την ροή θερμότητας προς μια περιοχή V μπορεί να μετασχηματιστεί στο ολοκλήρωμα όγκου

${\begin{aligned}q_{t}(V)&=-\int _{\partial V}\mathbf {H} (x)\cdot \mathbf {n} (x)\,dS\\&=\int _{\partial V}\mathbf {A} (x)\cdot \nabla u(x)\cdot \mathbf {n} (x)\,dS\\&=\int _{V}\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}\,dx\end{aligned}}$

• Ο χρονικός ρυθμός μεταβολής της θερμοκρασίας στο σημείο x είναι ανάλογος με την ροή θερμικής ενέργειας προς ένα τμήμα απειροστού όγκου, ;όπου η σταθερά αναλογίας εξαρτάται από μια σταθερά κ

$\partial _{t}u(x,t)=\kappa (x)Q(x,t)\,$

Συγκεντρώνοντας όλες αυτές τις εξισώσεις, παίρνουμε την γενική εξίσωση θερμικής ροής:

$\partial _{t}u(x,t)=\kappa (x)\sum _{i,j}\partial _{x_{i}}{\bigl (}a_{ij}(x)\partial _{x_{j}}u(x,t){\bigr )}$

Παρατηρήσεις.

• Ο συντελεστής κ(x) είναι η αντίστροφη της θερμοχωρητικότητας της ουσίας στο σημείο x επί την πυκνότητα της ουσίας στο σημείο x.
• Στη περίπτωση που το μέσο είναι ισότροπο, ο πίνακας A είναι ένας βαθμωτός πίνακας ίσος προς την θερμική αγωγιμότητα.
• Στη περίπτωση που το μέσο είναι ανισότροπο όπου ο πίνακας A δεν είναι βαθμωτός (π.χ., εξαρτάται από το x), τότε σπάνια μπορούμε να έχουμε έναν αναλυτικό τύπο για την εξίσωση θερμότητας. Παρ ' όλα αυτά ,είναι συνήθως δυνατό να λάβουμε υπ' όψιν μας το σχετικό αφηρημένο πρόβλημα Cauchy και να δείξουμε ότι είναι ένα καλά ορισμένο πρόβλημα και/ή να δείξουμε κάποιες ποιοτικές ιδιότητες (όπως διατήρηση των αρχικών θετικών δεδομένων, άπειρη ταχύτητα διάδοσης, σύγκλιση γύρω από ένα σημείο ισορροπίας, ιδιότητες εξομάλυνσης). Αυτό συνήθως γίνεται με την θεωρία ημιομάδων μονής παραμέτρου: για παράδειγμα, αν ο A είναι ένας συμμετρικός πίνακας, τότε ο ελλειπτικός τελεστής που ορίζεται παρακάτω

$Au(x):=\sum _{i,j}\partial _{x_{i}}a_{ij}(x)\partial _{x_{j}}u(x)$

είναι αυτοσυζυγής και σκεδαστικός, συνεπώς λόγω της φασματικής θεωρίας παράγει μια ημιομάδα μονής παραμέτρου.

Θεμελιώδης λύση

Μία θεμελιώδης λύση, που επίσης λέγεται πυρήνας θερμότητας , είναι μία λύση της εξίσωσης της θερμότητας αντίστοιχη στην αρχική συνθήκη από ένα αρχικό σημείο- πηγή της θερμότητας σε μία γνωστή θέση.Αυτό μπορεί να χρησιμοποιηθεί για να βρούμε μία γενική λύση της εξίσωσης της θερμότητας πάνω στο πεδίο ορισμού΄δες για παράδειγμα ( Evans,1998) για εισαγωγική αναφορά. Σε μία μεταβλητή,η συνάρτηση του Green είναι η λύση του προβλήματος αρχικής τιμής

${\begin{cases}u_{t}(x,t)-ku_{xx}(x,t)=0&(x,t)\in \mathbf {R} \times (0,\infty )\\u(x,0)=\delta (x)&\end{cases}}$

όπου δ είναι η συνάρτηση Dirac.Η λύση του προβλήματος είναι η θεμελιώδης λύση

$\Phi (x,t)={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right).$

Σε αρκετές χωρικές μεταβλητές, η θεμελιώδης λύση λύνει τα ανάλογα προβλήματα

${\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \mathbf {R} ^{n}\times (0,\infty )\\u(\mathbf {x} ,0)=\delta (\mathbf {x} )\end{cases}}$

Η "n"- ιοστή θεμελιώδης λύση είναι το προϊόν των θεμελιωδών λύσεων για κάθε μεταβλητή'για παράδειγμα,

$\Phi (\mathbf {x} ,t)=\Phi (x_{1},t)\Phi (x_{2},t)\dots \Phi (x_{n},t)={\frac {1}{\sqrt {(4\pi kt)^{n}}}}\exp \left(-{\frac {\mathbf {x} \cdot \mathbf {x} }{4kt}}\right).$

Η γενική λύση της εξίσωσης της θερμότητας για R ⁿ βρίσκεται με συνέλιξη,έτσι ώστε να λυθεί το πρόβλημα αρχικής τιμής με u(x, 0) = g(x), :$u(\mathbf {x} ,t)=\int _{\mathbf {R} ^{n}}\Phi (\mathbf {x} -\mathbf {y} ,t)g(\mathbf {y} )d\mathbf {y} .$

Το γενικό πρόβλημα σε ένα πεδίο ορισμού Ω στο Rⁿ είναι

${\begin{cases}u_{t}(\mathbf {x} ,t)-k\sum _{i=1}^{n}u_{x_{i}x_{i}}(\mathbf {x} ,t)=0&(\mathbf {x} ,t)\in \Omega \times (0,\infty )\\u(\mathbf {x} ,0)=g(\mathbf {x} )&\mathbf {x} \in \Omega \end{cases}}$

είτε με όριο δεδομένων τo πρόβλημα Dirichlet είτε το πρόβλημα του Neumann.Η συνάτηση του Green πάντοτε υπάρχει,αλλά αν το πεδίο ορισμού δεν μπορεί να αναλυθεί σε πρόβλημα μίας μεταβλητής(δες παρακάτω),πιθανόν να μην μπορεί γραφτεί ρητά.Άλλες μέθοδοι περιλαμβάνουν τη μέθοδο των εικόνων, το διαχωρισμό των μεταβλητών και το μετασχηματισμό Λαπλάς (Cole,2011).

Μερικές λύσεις της συνάρτησης Green μονοδιάστατες

Μία ποικιλία από λύσεις της συνάρτησης Green σε μία διάσταση αναφέρονται εδώ άλλες υπάρχουν αλλού. Σε μερικές από αυτές το πεδίο ορισμού είναι (−∞,∞). Σε άλλες είναι το (0,∞)είτε με τις οριακές συνθήκες του Neumann ή του Ντίριχλετ. Μία άλλη ποικιλία είναι εκείνη η οποία λύνει την ανομοιογενή εξίσωση :$u_{t}=ku_{xx}+f.$ όπου η f είναι μία συνάρτηση του χ και t.

Πρόβλημα στο (-∞,∞) αρχικών συνθηκών

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in \mathbf {R} \times (0,\infty )\\u(x,0)=0&IC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{-\infty }^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)f(y,s)\,dy\,ds$

Σχόλιο:Αυτή η λύση είναι η συνέλιξη στο 'R' ²,δηλαδή σε σχέση με τις μεταβλητές χ και t της θεμελιώδους λύσης

$\Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$

και της συνάρτησης f(x, t),όπως ορίζεται σε όλο το R² και 0 για όλα τα t → 0. Επαληθεύει πως

−

$\left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *f)=f,$

που εκφράζονται στη γλώσσα των διανομών

$\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi =\delta ,$

όπου η κατανομή δ είναι η Dirac συνάρτηση που είναι η αξιολόγηση σε 0.

Πρόβλημα στο (0,∞) με ομοιογενείς οριακές συνθήκες Dirichlet

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&IC\\u(0,t)=0&BC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$

Σχόλιο:Αυτή η λύση λαμβάνεται από τον προηγούμενο τύπο όπως εφαρμόζεται στα δεδομένα f(x, t) κατάλληλα επεκτεταμένα στο R × [0,∞),ώστε να είναι μία περιττή συνάρτηση της μεταβλητής χ,δηλαδή επιτρέποντας f(−x, t) := −f(x, t) για όλα τα χ και t.Αντίστοιχα,η λύση του ανομοιογενούς προβλήματος στο (−∞,∞) είναι μία περιττή συνάρτηση σε σχέση με τη μεταβλητή χγια όλες τις τιμές του t και ειδικότερα πληροί τις ομοιογενείς οριακές συνθήκες Dirichlet u(0, t) = 0.

Πρόβλημα στο (0,∞) με ομοιογενείς οριακές συνθήκες του Neumann

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&IC\\u_{x}(0,t)=0&BC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$

Σχόλιο.Αυτή η λύση λαμβάνεται από τον πρώτο τύπο όπως εφαρμόζεται στα δεδομένα f(x, t) κατάλληλα επεκτεταμένο στο R × [0,∞),ώστε να είναι μία ακόμη συνάρτηση της μεταβλητής χ,δηλαδή αφήνοντας f(−x, t) := f(x, t) για όλα τα χ και t.Αντίστοιχα,η λύση του ανομοιογενούς προβλήματος στο (−∞,∞) είναι μία συνάρτηση σε σχέση με τη μεταβλητή χγια όλες τις τιμές του t και ειδικότερα είναι μία ομαλή συνάρτηση που πληροί τις ομοιογενείς οριακές συνθήκες του Neumann u_x(0, t) = 0.

Πρόβλημα στο (0,∞) ομοιογενών και μη ομοιγενών αρχικών συνθηκών του Dirichlet

${\begin{cases}u_{t}=ku_{xx}&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&IC\\u(0,t)=h(t)&BC\end{cases}}$

$u(x,t)=\int _{0}^{t}{\frac {x}{\sqrt {4\pi k(t-s)^{3}}}}\exp \left(-{\frac {x^{2}}{4k(t-s)}}\right)h(s)\,ds,\qquad \forall x>0$

Σχόλιο.Αυτή η συνάρτηση είναι συνέλιξη με αναφορά στη μεταβλητή t

$\psi (x,t):=-2k\partial _{x}\Phi (x,t)={\frac {x}{\sqrt {4\pi kt^{3}}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$

και στη συνάρτηση h(t).Από τότε που η Φ(x, t) είναι η θεμελιώδης λύση της

$\partial _{t}-k\partial _{x}^{2},$

η συνάρτηση ψ(x, t) είναι επίσης μία λύση της ίδιας εξίσωσης θερμότητας, και τελικά είναι u := ψ ∗ h, με τις γενικές ιδιότητες της συνέλιξης.Περισσότερο,

$\psi (x,t)={\frac {1}{x^{2}}}\,\psi \left(1,{\frac {t}{x^{2}}}\right)$

$\int _{0}^{\infty }\psi (x,t)\,dt=1,$

έτσι ώστε από τη γενική αλήθεια σχετικά με προσέγγιση στην ταυτότητα ψ(x, ⋅) ∗ h → h as x → 0 για τη συγκεκριμένη h.

Το πρόβλημα στο (-∞,∞) με ομοιογενείς αρχικές συνθήκες

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in \mathbf {R} \times (0,\infty )\\u(x,0)=0&IC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{-\infty }^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)f(y,s)\,dy\,ds$

΄΄΄Σχόλιο.Αυτή η εξίσωση είναι η συνέλιξη R²,σε σχέση με δύο μεταβλητές x και t, της θεμελιώδης λύσης

$\Phi (x,t):={\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$

και της συνάρτησης f(x, t),όπως ορίζονται σε όλο το R² και για όλα τα t που τείνουν στο 0 δίνουν την τιμή 0.

$\left(\partial _{t}-k\partial _{x}^{2}\right)(\Phi *f)=f,$

που στη γλώσσα των κατανομών μετατρέπεται σε

$\left(\partial _{t}-k\partial _{x}^{2}\right)\Phi =\delta ,$

όπου δ είναι η συνάρτηση Dirac,η οποία εκτιμάται στο 0.

Πρόβλημα σε (0,∞) με οριακές αρχικές συνθήκες Dirichlet και αρχικές συνθήκες

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&IC\\u(0,t)=0&BC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)-\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$

Σχόλιο.Αυτή η λύση παρατηρείται από τον τύπο όπως εφαρμόζεται για δεδομένα f(x, t) κατάλληλα επεκτεταμένα στο R × [0,∞),ώστε γίνεται περιττή συνάρτηση της μεταβλητής x,θέτοντας f(−x, t) := −f(x, t) για όλα τα x και t.Η λύση του ανομοιογενούς προβλήματος στο (−∞,∞) είναι μία περιττή συνάρτηση για τη μεταβλητή x και όλες τις τιμές του t,και ικανοποιεί τις ομοιογενείς οριακές συνθήκες Dirichlet u(0, t) = 0.

Πρόβλημα στο (0,∞) με ομοιογενείς οριακές συνθήκες Neumann και αρχικές συνθήκες

${\begin{cases}u_{t}=ku_{xx}+f(x,t)&(x,t)\in [0,\infty )\times (0,\infty )\\u(x,0)=0&IC\\u_{x}(0,t)=0&BC\end{cases}}$

$u(x,t)=\int _{0}^{t}\int _{0}^{\infty }{\frac {1}{\sqrt {4\pi k(t-s)}}}\left(\exp \left(-{\frac {(x-y)^{2}}{4k(t-s)}}\right)+\exp \left(-{\frac {(x+y)^{2}}{4k(t-s)}}\right)\right)f(y,s)\,dy\,ds$

Σχόλιο.Η λύση παρατηρείται από τον πρώτο τύπο όπως εφαρμόζεται σε δεδομένα f(x, t) καταλλήλως επεκτεταμένα σε R × [0,∞),ώστε να γίνει μία συνάρτηση του x,θέτοντας f(−x, t) := f(x, t) για όλα τα x και t.Η λύση από το ανομοιογενές πρόβλημα στο (−∞,∞) είναι μία συνάρτηση με τη μεταβλητή x για όλες τις τιμές του t,και ικανοποιεί τις ομοιογενείς οριακές συνθήκες του Neumann u_x(0, t) = 0.

Παραδείγματα

Επειδή η εξίσωση της θερμότητας είναι γραμμική,λύσεις από άλλους συνδυασμούς οριακών συνθηκών,ανομοιογενούς όρου και αρχικών συνθηκών μπορούν να βρεθούν παίρνοντας έναν κατάλληλο γραμμικό συνδυασμόαπό τις παραπάνω λύσεις της συνάρτησης του Green.

Για παράδειγμα, για να λύσεις

:${\begin{cases}u_{t}=ku_{xx}+f&(x,t)\in \mathbf {R} \times (0,\infty )\\u(x,0)=g(x)&IC\end{cases}}$

βάζοντας u = w + v όπου w, v,και r λύνουν τα προβλήματα

:${\begin{cases}v_{t}=kv_{xx}+f,\,w_{t}=kw_{xx}\,&(x,t)\in \mathbf {R} \times (0,\infty )\\v(x,0)=0,\,w(x,0)=g(x)\,&IC\end{cases}}$

Ιδιότητα της μέσης τιμής για την εξίσωση της θερμότητας

Λύσεις της εξίσωσης θερμότητας

$(\partial _{t}-\Delta )u=0$

ικανοποιούν την ιδιότητα της μέσης τιμής ανάλογα με τις ιδιότητες των μέσων τιμών των αρμονικών συναρτήσεων,λύσεις

:$\Delta u=0$,

αν και λίγο πολύπλοκη.Ακριβώς,αν u λύνει

$(\partial _{t}-\Delta )u=0$

και

$(x,t)+E_{\lambda }\subset \mathrm {dom} (u)$

τότε

$u(x,t)={\frac {\lambda }{4}}\int _{E_{\lambda }}u(x-y,t-s){\frac {|y|^{2}}{s^{2}}}ds\,dy,$

όπου E_λ είναι μία θερμή μπάλα,που αποτελεί υπερσύνολο της θεμελιώδους λύσης της εξίσωσης θερμότητας:

$E_{\lambda }:=\{(y,s)\,:\,\Phi (y,s)>\lambda \},$

$\Phi (x,t):=(4t\pi )^{-{\frac {n}{2}}}\exp \left(-{\frac {|x|^{2}}{4t}}\right).$

Σημείωσε πως

$\mathrm {diam} (E_{\lambda })=o(1)$

καθώς το λ → ∞ ώστε ο πάνω τύπος να ισχύει για κάθε (x, t) στο ανοιχτό σύνολο dom(u) για λ αρκετά μεγάλο.Αντίθετα,κάθε συνάρτηση ικανοποιεί την παραπάνω ιδιότητα της μέσης τιμής σε μία ανοιχτή περιοχή του Rⁿ × R είναι μία λύση της εξίσωσης θερμότητας.Αυτό μπορεί να δειχθεί με ένα επιχείρημα παρόμοιο με το ανάλογο ενός από αρμονικές συναρτήσεις.

Σταθερή εξίσωση θερμότητας

Η σταθερή εξίσωση θερμότητας δεν εξαρτάται από το χρόνο.Με άλλα λόγια υπάρχουν συνθήκες τέτοιες ώστε:

${\frac {\partial u}{\partial t}}=0$

Αυτή η συνθήκη εξαρτάται από το σταθερό χρόνο και από το χρόνο που πέρασε από τότε που επιβλήθηκαν οι οριακές συνθήκες.Έτσι,η προϋπόθεση αυτή πληρούται στις περιπτώσεις στις οποίες ο χρόνος είναι αρκετά γρήγορος ώστε η πιο περίπλοκη χρονοεξαρτώμενη εξίσωση της θερμότητας από τη σταθερή περίπτωση.Ισοδύναμα,η σταθερή κατάσταση υπάρχει για όλες τις περιπτώσεις για τις οποίες έχει περάσει αρκετός χρόνος ώστε το θερμικό πεδίο u πλέον δεν εξελίσσεται στο χρόνο.

Στην στατική περίπτωση , μια χωρική θερμική κλίση μπορεί ( ή δεν μπορεί ) να υπάρχει , αλλά αν υπάρχει , αυτό δεν αλλάζει στο χρόνο . Επομένως, η παρούσα εξίσωση περιγράφει το τελικό αποτέλεσμα σε όλα τα θερμικά προβλήματα στα οποία μία πηγή ενεργοποιείται (για παράδειγμα, ένας κινητήρας που ξεκίνησε σε ένα αυτοκίνητο ) , και αρκετός χρόνος έχει περάσει για όλες τις μόνιμες βαθμίδες θερμοκρασίας ώστε να εγκατασταθούν στο χώρο, μετά δε αυτά τα χωρικές βαθμίδες δεν αλλάζουν πλέον στο χρόνο ( όπως και πάλι , με ένα αυτοκίνητο στο οποίο ο κινητήρας έχει λειτουργήσει για αρκετά μεγάλο χρονικό διάστημα ) . Η άλλη ( τετριμμένη ) λύση είναι για όλες τους βαθμούς θερμοκρασίας για να εξαφανιστούν , καθώς, στην περίπτωση αυτή η θερμοκρασία γίνει ομοιόμορφh στο χώρο. Η εξίσωση είναι πιο απλή και μπορεί να βοηθήσει να κατανοήσουμε καλύτερα τη φυσική των υλικών , χωρίς να εστιάζει στη δυναμική της διαδικασίας μεταφοράς θερμότητας . Χρησιμοποιείται ευρέως για απλά προβλήματα μηχανικής υποθέτοντας πως υπάρχει ισορροπία των πεδίων θερμοκρασίας και θερμότητα μεταφοράς , με το χρόνο.

Σταθερή συνθήκη:

${\frac {\partial u}{\partial t}}=0$

Η στατική εξίσωση θερμότητας για έναν όγκο που περιέχει μια πηγή θερμότητας ( την ανομοιογενή περίπτωση ) , είναι η εξίσωση του Poisson:

$k\nabla ^{2}u=q$

όπου u είναι η θερμοκρασία , k είναι η θερμική αγωγιμότητα και q η θερμική πυκνότητα ροής της πηγής .

Στην ηλεκτροστατική, αυτό είναι ισοδύναμο με την περίπτωση όπου ο χώρος υπό εξέταση περιέχει ένα ηλεκτρικό φορτίο .

Η στατική εξίσωση θερμότητας χωρίς μια πηγή θερμότητας εντός του όγκου (η ομοιογενής περίπτωση ) είναι η εξίσωση στην ηλεκτροστατική για όγκο ελεύθερου χώρου που δεν περιέχει ένα φορτίο . Περιγράφεται από την εξίσωση Λαπλάς:

$\nabla ^{2}u=0$

Θερμική διάχυση σε πολυμερή

Μία άμεση εφαρμογή της εξίσωσης της θερμότητας,σε συνδυασμό με τη Fourier θεωρία, σε σφαιρικές συντεταγμένες,είναι η πρόβλεψη των προφίλ θερμικής μεταφοράς και η μέτρηση της θερμικής διάχυσης σε πολυμερή (Unsworth και Duarte). Αυτή η διπλή θεωρητική-πειραματική μέθοδος εφαρμόζεται σε καουτσούκ,διάφορα άλλα πολυμερή υλικά πρακτικού ενδιαφέροντος και σε υγρά.Οι συγγραφείς αυτοί προέρχονται από μία έκφραση της θερμοκρασίας στο κλεντρο της σφαίρας T_C

${\frac {T_{C}-T_{S}}{T_{0}-T_{S}}}=2\sum _{n=1}^{\infty }(-1)^{n+1}\exp \left({-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}\right)$

όπου T₀ είναι η αρχική θερμοκρασία της σφαίρας και T_S η θερμοκρασία στην επιφάνεια της σφαίρας,ακτίνας L.Αυτή η εξίσωση έχει επίσης βρει εφαρμογές στη μεταφορά πρωτεϊνης και στα θερμικά μοντέλα στη φυσική.

Διάχυση σωματιδίων

Κύριο άρθρο:Εξίσωση διάχυσης Κάποιος μπορεί να μοντελοποιήσει διάχυση με μία εξίσωση περιλαμβάνοντας:

• την ογκομετρική συγκέντρωση των σωματιδίων, συμβολίζοντας c,στην περίπτωση τηςσυλλογικής διάχυσης ενόα μεγάλου αρθμού σωματιδίων, ή

• τη συνάρτηση πυκνότητας πιθανότητας που σχετίζεται με τη θέση ενός μεμονωμένου σωματιδίου,που συμβολίζεται με p.

Σε κάθε περίπτωση,χρησιμοποιείς την εξίσωση της θερμότητας

$c_{t}=D\Delta c,\quad$

ή

$P_{t}=D\Delta P.\quad$

Οι c και Pείναι συναρτήσεις της θέσης και του χρόνου.D είναι ο συντελεστής διάχυσης που ελέγχει την ταχύτητα της διαδικασίας της διάχυσης,και τυπικά εκφράζεται σε μέτρο στο τετράγωνο ανά δευτερόλεπτο.Αν ο συντελεστής διάχυσης D δεν είναι σταθερός,αλλά εξαρτάται από τη συγκέντρωση c(ή Pστη δεύτερη περίπτωση),τότε παίρνει την μη γραμμική εξίσωση διάχυσης.

Κίνηση Brown

Βάζοντας τη σταχαστική διαδικασία $X$ να είναι η λύση της διαφορετικής στοχαστικής εξίσωσης

$\left\{{\begin{array}{ll}{\text{d}}X_{t}={\sqrt {2k}}{\text{d}}B_{t}\\X_{0}=0\end{array}}\right.$

όπου $B$ είναι Wiener διαδικασία (καθορισμένη Brownian κίνηση). Τότε η συνάρτηση πυυκνότητας πιθανότητας $X$ δίνεται κάθε φορά $t$ από

${\frac {1}{\sqrt {4\pi kt}}}\exp \left(-{\frac {x^{2}}{4kt}}\right)$

που είναι η λύση του προβλήματος αρχικής τιμής

$\left\{{\begin{array}{ll}u_{t}(x,t)-ku_{xx}(x,t)=0,\quad (x,t)\in \mathbb {R} \times (0,+\infty )\\u(x,0)=\delta (x)\end{array}}\right.$

όπου $\delta$ είναι η Dirac delta συνάρτηση.

Η εξίσωση Schrödinger για ένα ελεύθερο σωματίδιο

− {{|Schrödinger εξίσωση}}

Με μία απλή διαίρεση,η Schrödinger εξίσωση για ένα μονό σωματίδιο από μάζα m σε απουσία κάθε εφαρμοσμένου πεδίου δύναμης μπορεί να ξαναγραφτεί με τον ακόλουθο τρόπο:

$\psi _{t}={\frac {i\hbar }{2m}}\Delta \psi$,

όπου i είναι η φανταστική μονάδα, ħ είναι reduced Planck's σταθερά, και ψ είναι η κυματική συνάρτηση του σωματιδίου.

Αυτή η εξίσωση είναι τυπικά όμοια με την εξίσωση διάχυσης των σωματιδίων που λαμβάνεται μέσω του ακόλουθου μετασχηματισμού:

${\begin{aligned}c(\mathbf {R} ,t)&\to \psi (\mathbf {R} ,t)\\D&\to {\frac {i\hbar }{2m}}\end{aligned}}$

Εφαρμόζοντας αυτό το μετασχηματισμό στις συναρτήσεις του Green ορισμένες στην περίπτωση των σωματιδίων διάχυσης δίνει την Schrödinger εξίσωση,η οποία με τη σειρά της χρησιμοποιείται για την κυματική συνάρτηση μέσω ενός ολοκληρώματος της κυματικής συνάρτησης για

t = 0:

$\psi (\mathbf {R} ,t)=\int \psi (\mathbf {R} ^{0},t=0)G(\mathbf {R} -\mathbf {R} ^{0},t)dR_{x}^{0}\,dR_{y}^{0}\,dR_{z}^{0},$

με

$G(\mathbf {R} ,t)={\bigg (}{\frac {m}{2\pi i\hbar t}}{\bigg )}^{3/2}e^{-{\frac {\mathbf {R} ^{2}m}{2i\hbar t}}}.$

Παρατήρηση:αυτή η αναλογία μεταξύ της κβαντομηχανικής και της διάχυσης είναι καθαρά τυπική.Φυσικά,η εξέλιξη της κυματικής συνάρτησης ικανοποιώντας την Schrödinger εξίσωση θα μπορούσε να έχει προέλευση διάφορη της διάχυσης.

Θερμική διάχυση σε πολυμερή

Μία άμεση εφαρμογή της εξίσωσης της θερμότητας,σε συνδυασμό με τη Fourier θεωρία, σε σφαιρικές συντεταγμένες,είναι η πρόβλεψη των προφίλ θερμικής μεταφοράς και η μέτρηση της θερμικής διάχυσης σε πολυμερή (Unsworth και Duarte). Αυτή η διπλή θεωρητική-πειραματική μέθοδος εφαρμόζεται σε καουτσούκ,διάφορα άλλα πολυμερή υλικά πρακτικού ενδιαφέροντος και σε υγρά.Οι συγγραφείς αυτοί προέρχονται από μία έκφραση της θερμοκρασίας στο κλεντρο της σφαίρας T_C

−

${\frac {T_{C}-T_{S}}{T_{0}-T_{S}}}=2\sum _{n=1}^{\infty }(-1)^{n+1}\exp \left({-{\frac {n^{2}\pi ^{2}\alpha t}{L^{2}}}}\right)$

− όπου T₀ είναι η αρχική θερμοκρασία της σφαίρας και T_S η θερμοκρασία στην επιφάνεια της σφαίρας,ακτίνας L.Αυτή η εξίσωση έχει επίσης βρει εφαρμογές στη μεταφορά πρωτεϊνης και στα θερμικά μοντέλα στη φυσική.

Κι άλλες εφαρμογές

Η εξίσωση της θερμότητας προκύπτει στο modeling από ένα αριθμό φαινομένων και συχνά χρησιμοποιείται στα οικονομικά μαθηματικά στη μοντελοποίηση options.Η διάσημη Black–Scholes διαφορική εξίσωση μπορεί να μετατραπεί σε εξίσωση θερμότητας που επιτρέπει σχετικά εύκολα λύσεις από ένα οικείο όργανο μαθηματικών.Πολλές από τις επεκτάσεις των απλών μοντέλων επιλογής δεν έχουν λύσεις και ως εκ τούτου πρέπει να λυθούν αριθμητικά για να αποκτήσουν μία μοντελοποιημένη τιμή.Η εξίσωση που περιγράφει την πίεση της διάχυσης σε ένα πορώδες μέσο είναι πανομοιότυπη στη μορφή με την αξίσωση θερμότητας.Προβλήματα διάχυσης που ασχολούνται με [[

Dirichlet οριακές συνθήκες|Dirichlet]], Neumann και Robin οριακές συνθήκες έχουν κλειστή μορφή αναλυτικών λύσεων (Thambynayagam 2011).

Η εξίσωση της θερμότητας χρησιμοποιείται ευρέως στην ανάλυση εικόνας (Perona & Malik 1990) και στη μηχανική μάθηση όπως τη θεωρία οδήγησης πίσω από τις scale-space ή graph Laplacians μεθόδους.Η εξίσωση της θερμότητας μπορεί να λυθεί αποτελεσματικά αριθμητικώς χρησιμοποιώντας τη Crank–Nicolson method του (Crank & Nicolson 1947).Αυτή η μέθοδος μπορεί να επεκταθεί σε πολλά μοντέλα χωρίς κλειστού τύπου λύσεις,βλέπε για παράδειγμα (Wilmott, Howison & Dewynne 1995).

Μία αφηρημένη μορφή της εξίσωσης της θερμότητας manifolds παρέχει μία σημαντική προσέγγιση για το Atiyah–Singer index theorem,και έχει οδηγήσει σε περεταίρω εργασίες για την εξίσωση της θερμότητας στη Riemannian geometry.