Πραγματικός αριθμός: Διαφορά μεταξύ των αναθεωρήσεων
μ Ρομπότ: Προσθήκη: gan:實數 |
Xqbot (συζήτηση | συνεισφορές) μ Ρομπότ: Τροποποίηση: tr:Reel sayılar; διακοσμητικές αλλαγές |
||
| Γραμμή 1: | Γραμμή 1: | ||
Στα [[μαθηματικά]], οι '''πραγματικοί αριθμοί''' γίνονται αντιληπτοί διαισθητικά ως το [[σύνολο]] όλων των αριθμών που είναι σε [[ένα προς ένα αντιστοιχία]] με τα [[σημείο|σημεία]] μιας άπειρης [[ευθεία|ευθείας]], που καλείται ''ευθεία των πραγματικών αριθμών'' ή ''πραγματικός άξονας''. Ο όρος "πραγματικός αριθμός" πλάστηκε εκ των υστέρων σε αντιδιαστολή προς τους "[[φανταστικός αριθμός|φανταστικούς αριθμούς]]", των οποίων η ένωση με τους πραγματικούς δίνει τους [[μιγαδικοί αριθμοί|μιγαδικούς]]. Οι πραγματικοί αριθμοί είναι το κεντρικό αντικείμενο μελέτης της [[πραγματική ανάλυση|πραγματικής ανάλυσης]]. Σε αυστηρή μαθηματική γλώσσα, ο πραγματικός αριθμός ορίζεται ως εξής: |
Στα [[μαθηματικά]], οι '''πραγματικοί αριθμοί''' γίνονται αντιληπτοί διαισθητικά ως το [[σύνολο]] όλων των αριθμών που είναι σε [[ένα προς ένα αντιστοιχία]] με τα [[σημείο|σημεία]] μιας άπειρης [[ευθεία|ευθείας]], που καλείται ''ευθεία των πραγματικών αριθμών'' ή ''πραγματικός άξονας''. Ο όρος "πραγματικός αριθμός" πλάστηκε εκ των υστέρων σε αντιδιαστολή προς τους "[[φανταστικός αριθμός|φανταστικούς αριθμούς]]", των οποίων η ένωση με τους πραγματικούς δίνει τους [[μιγαδικοί αριθμοί|μιγαδικούς]]. Οι πραγματικοί αριθμοί είναι το κεντρικό αντικείμενο μελέτης της [[πραγματική ανάλυση|πραγματικής ανάλυσης]]. Σε αυστηρή μαθηματική γλώσσα, ο πραγματικός αριθμός ορίζεται ως εξής: |
||
Άν |
Άν για τον αριθμό L ισχύει <math>\lim_{n \to \infty}a_n = L </math> , όπου a<sub>n</sub> μια ρητή προσέγγιση του L με n δεκαδικά ψηφία, τότε ο L είναι πραγματικός αριθμός. Αυτό σημαίνει ότι πραγματικός είναι ο αριθμός του οποίου μπορούμε να γράψουμε μια δεκαδική προσέγγιση, όπως στον αριθμό [[αριθμός π|π]]~3,14. |
||
Οι πραγματικοί αριθμοί διακρίνονται σε [[ρητός αριθμός|ρητούς αριθμούς]] (που μπορούν να εκφραστούν ως κλάσματα με ακέραιο αριθμητή και παρονομαστή) και σε [[άρρητος αριθμός|άρρητους αριθμούς]] (που δεν μπορούν να εκφραστούν επακριβώς ως κλάσματα). Οι ρητοί μαζί με τους άρρητους αποτελούν ένα συνεχές. |
Οι πραγματικοί αριθμοί διακρίνονται σε [[ρητός αριθμός|ρητούς αριθμούς]] (που μπορούν να εκφραστούν ως κλάσματα με ακέραιο αριθμητή και παρονομαστή) και σε [[άρρητος αριθμός|άρρητους αριθμούς]] (που δεν μπορούν να εκφραστούν επακριβώς ως κλάσματα). Οι ρητοί μαζί με τους άρρητους αποτελούν ένα συνεχές. |
||
| Γραμμή 7: | Γραμμή 7: | ||
Κάθε "φυσικό [[μέγεθος]]" που μπορεί να μετρηθεί εκφράζεται συνήθως με έναν πραγματικό αριθμό. Το σύνολο των πραγματικών αριθμών συμβολίζεται με <math>\R</math>. |
Κάθε "φυσικό [[μέγεθος]]" που μπορεί να μετρηθεί εκφράζεται συνήθως με έναν πραγματικό αριθμό. Το σύνολο των πραγματικών αριθμών συμβολίζεται με <math>\R</math>. |
||
==Αξιωματική Θεμελίωση των Πραγματικών Αριθμών== |
== Αξιωματική Θεμελίωση των Πραγματικών Αριθμών == |
||
Ονομάζουμε σύνολο των πραγματικών αριθμών ένα σύνολο <math>\R</math> το οποίο ικανοποιά τα παρακάτω τρία αξιώματα: |
Ονομάζουμε σύνολο των πραγματικών αριθμών ένα σύνολο <math>\R</math> το οποίο ικανοποιά τα παρακάτω τρία αξιώματα: |
||
*Το σύνολο <math>\R</math> αποτελεί [[Σώμα (άλγεβρα)|σώμα]]. Αναλυτικά: |
* Το σύνολο <math>\R</math> αποτελεί [[Σώμα (άλγεβρα)|σώμα]]. Αναλυτικά: |
||
** Για όλα τα x, y, και z στο <math>\R</math>, ισχύει x + (y + z) = (x + y) + z and x(yz) = (xy)z. |
** Για όλα τα x, y, και z στο <math>\R</math>, ισχύει x + (y + z) = (x + y) + z and x(yz) = (xy)z. |
||
** Για όλα τα x και y στο <math>\R</math>, x + y = y + x και xy = yx. |
** Για όλα τα x και y στο <math>\R</math>, x + y = y + x και xy = yx. |
||
| Γραμμή 15: | Γραμμή 15: | ||
** Για όλα τα x στο <math>\R</math>, υπάρχει ένα στοιχείο 0, τέτοιο ώστε x + 0 = x = 0 + x και ένα στοιχείο 1 <math>\neq</math> 0, τέτοιο ώστε x1 = x = 1x. |
** Για όλα τα x στο <math>\R</math>, υπάρχει ένα στοιχείο 0, τέτοιο ώστε x + 0 = x = 0 + x και ένα στοιχείο 1 <math>\neq</math> 0, τέτοιο ώστε x1 = x = 1x. |
||
** Για όλα τα x στο <math>\R</math>, υπάρχει ένα στοιχείο −x στο R, τέτοιο ώστε x + (−x) = 0 = (-x) + x. |
** Για όλα τα x στο <math>\R</math>, υπάρχει ένα στοιχείο −x στο R, τέτοιο ώστε x + (−x) = 0 = (-x) + x. |
||
** Για όλα τα x ≠ 0 στο <math>\R</math>, υπάρχει ένα στοιχείο x<sup> |
** Για όλα τα x ≠ 0 στο <math>\R</math>, υπάρχει ένα στοιχείο x<sup>−1</sup> στο R, τέτοιο ώστε xx <sup>−1</sup> = 1 = x <sup>−1</sup> x. |
||
*Το σώμα <math>\R</math> είναι [[Διάταξη|διατεταγμένο]]. Αναλυτικά για |
* Το σώμα <math>\R</math> είναι [[Διάταξη|διατεταγμένο]]. Αναλυτικά για x, y, και z στο <math>\R</math> |
||
** ισχύει ακριβώς μια από τις: x<y, x=y, x>y (τριχοτομία) |
** ισχύει ακριβώς μια από τις: x<y, x=y, x>y (τριχοτομία) |
||
** αν x<y τότε x+z<y+z |
** αν x<y τότε x+z<y+z |
||
** αν x>0 και y>0 τότε xy>0. |
** αν x>0 και y>0 τότε xy>0. |
||
*Το διατεταγμένο σώμα <math>\R</math> είναι [[πλήρες]]: Κάθε μη κένό άνω [[Φράγμα (μαθηματικά)|φραγμένο]] υποσύνολό του έχει ένα ελάχιστο άνω φράγμα (suprimum). |
* Το διατεταγμένο σώμα <math>\R</math> είναι [[πλήρες]]: Κάθε μη κένό άνω [[Φράγμα (μαθηματικά)|φραγμένο]] υποσύνολό του έχει ένα ελάχιστο άνω φράγμα (suprimum). |
||
:Ισοδύναμα μπορούμε να ορίσουμε την πληρότητα με τον ορισμό στους μετρικούς χώρους, δηλαδή κάθε [[ακολουθία Κωσύ]] συγλίνει. |
:Ισοδύναμα μπορούμε να ορίσουμε την πληρότητα με τον ορισμό στους μετρικούς χώρους, δηλαδή κάθε [[ακολουθία Κωσύ]] συγλίνει. |
||
Αποδεικνύεται ότι όλα τα σύνολα που ικανοποιούν τα παραπάνω τρία αξιώματα είναι [[Ισομορφισμός|ισομορφικά]], κάτι που μας επιτρέπει να λέμε ότι υπάρχει μόνο '''ένα''' [[πλήρες διατεταγμένο σώμα]], το σύνολο των πραγματικών αριθμών. Το σύνολο <math>\Q</math> |
Αποδεικνύεται ότι όλα τα σύνολα που ικανοποιούν τα παραπάνω τρία αξιώματα είναι [[Ισομορφισμός|ισομορφικά]], κάτι που μας επιτρέπει να λέμε ότι υπάρχει μόνο '''ένα''' [[πλήρες διατεταγμένο σώμα]], το σύνολο των πραγματικών αριθμών. Το σύνολο <math>\Q</math> των ρητών αν και είναι διατεταγμένο σώμα δεν ικανοποιεί την [[Αρχή της πληρότητας]] ενώ τα σύνολα των φυσικών και ακεραίων δεν αποτελούν σώματα. |
||
==Κατασκευή== |
== Κατασκευή == |
||
Για την κατασκευή των πραγματικών αριθμών χρησιμοποιούμε ως αφετερία το σύνολο των ρητών αριθμών <math>\Q</math>. |
Για την κατασκευή των πραγματικών αριθμών χρησιμοποιούμε ως αφετερία το σύνολο των ρητών αριθμών <math>\Q</math>. |
||
Ζητούμε ένα σύνολο που είναι διατεταγμένο σώμα όπως το <math>\Q</math> και επιπλέον ικανοποιεί το αξίωμα της πληρότητας. |
Ζητούμε ένα σύνολο που είναι διατεταγμένο σώμα όπως το <math>\Q</math> και επιπλέον ικανοποιεί το αξίωμα της πληρότητας. |
||
| Γραμμή 43: | Γραμμή 43: | ||
==Η ευθεία των πραγματικών αριθμών== |
== Η ευθεία των πραγματικών αριθμών == |
||
Το σύνολο των πραγματικών αριθμών μπορεί να παρασταθεί σε μια [[ευθεία]], της οποίας κάθε [[σημείο]] αντιστοιχεί σε έναν μοναδικό πραγματικό αριθμό. Στην ευθεία αυτή, τα σημεία είναι διατεταγμένα έτσι ώστε κινούμενοι από αριστερά προς τα δεξιά η τιμή των πραγματικών αριθμών να αυξάνεται. Έτσι, επιλέγοντας ένα σημείο x, κάθε σημείο αριστερά από αυτό αντιστοιχεί σε πραγματικό αριθμό μικρότερο από αυτόν που αντιστοιχεί στο x, ενώ κάθε σημείο δεξιά απ'αυτό αντιστοιχεί σε μεγαλύτερο πραγματικό αριθμό. Αν x=0, τότε αριστερά βρίσκονται όλα τα σημεία που αντιστοιχούν στους αρνητικούς πραγματικούς αριθμούς, ενώ δεξιά βρίσκονται τα σημεία που αντιστοιχούν στους θετικούς. |
Το σύνολο των πραγματικών αριθμών μπορεί να παρασταθεί σε μια [[ευθεία]], της οποίας κάθε [[σημείο]] αντιστοιχεί σε έναν μοναδικό πραγματικό αριθμό. Στην ευθεία αυτή, τα σημεία είναι διατεταγμένα έτσι ώστε κινούμενοι από αριστερά προς τα δεξιά η τιμή των πραγματικών αριθμών να αυξάνεται. Έτσι, επιλέγοντας ένα σημείο x, κάθε σημείο αριστερά από αυτό αντιστοιχεί σε πραγματικό αριθμό μικρότερο από αυτόν που αντιστοιχεί στο x, ενώ κάθε σημείο δεξιά απ'αυτό αντιστοιχεί σε μεγαλύτερο πραγματικό αριθμό. Αν x=0, τότε αριστερά βρίσκονται όλα τα σημεία που αντιστοιχούν στους αρνητικούς πραγματικούς αριθμούς, ενώ δεξιά βρίσκονται τα σημεία που αντιστοιχούν στους θετικούς. |
||
| Γραμμή 51: | Γραμμή 51: | ||
Στον πραγματικό άξονα, αυτό σημαίνει ότι αν επιλέξουμε δύο σημεία α και β πάνω του, τότε ή το α είναι αριστερά του β ή το α θα συμπέσει με το β ή το α θα είναι δεξιά του β. Η πρόταση αυτή ακούγεται προφανής. |
Στον πραγματικό άξονα, αυτό σημαίνει ότι αν επιλέξουμε δύο σημεία α και β πάνω του, τότε ή το α είναι αριστερά του β ή το α θα συμπέσει με το β ή το α θα είναι δεξιά του β. Η πρόταση αυτή ακούγεται προφανής. |
||
[[ |
[[Αρχείο: Recta_real_entero_o_decimal_exacto.png|right]]Η ευθεία των πραγματικών αριθμών δεν διακόπτεται και πουθενά δεν έχει κενά. Αντίστοιχα, το [[σύνολο]] των πραγματικών αριθμών είναι τόσο πυκνό που πάντα μεταξύ δύο πραγματικών αριθμών, όσο μικρή [[Απόσταση (γεωμετρία)|απόσταση]] κι αν έχουν μεταξύ τους, θα υπάρχει τουλάχιστον ακόμη ένας. |
||
==Πληθάριθμος== |
== Πληθάριθμος == |
||
Το σύνολο των πραγματικών αριθμών είναι '''υπεραριθμήσιμο'''. Σε αντίθεση δηλαδή με τους [[φυσικός αριθμός|φυσικούς αριθμούς]] δεν μπορούμε να απαριθμίσουμε όλους τους πραγματικούς. |
Το σύνολο των πραγματικών αριθμών είναι '''υπεραριθμήσιμο'''. Σε αντίθεση δηλαδή με τους [[φυσικός αριθμός|φυσικούς αριθμούς]] δεν μπορούμε να απαριθμίσουμε όλους τους πραγματικούς. |
||
Ο [[πληθάριθμος]] του <math>\R</math> συμβολίζεται με τον ''πληθάριθμο του συνεχούς'' <math>\mathfrak c</math>. |
Ο [[πληθάριθμος]] του <math>\R</math> συμβολίζεται με τον ''πληθάριθμο του συνεχούς'' <math>\mathfrak c</math>. |
||
| Γραμμή 60: | Γραμμή 60: | ||
==Τοπολογικές ιδιότητες== |
== Τοπολογικές ιδιότητες == |
||
Το σύνολο των πραγματικών αριθμών μαζί με την [[ευκλείδεια μετρική]] αποτελούν [[μετρικός χώρος|μετρικό χώρο]]. |
Το σύνολο των πραγματικών αριθμών μαζί με την [[ευκλείδεια μετρική]] αποτελούν [[μετρικός χώρος|μετρικό χώρο]]. |
||
Η συνήθης [[τοπολογία]] προκύπτει από ανοιχτα διαστήματα της μορφής <math>B_r(p)=\{x\in\R:|x-p|<r\}</math>. |
Η συνήθης [[τοπολογία]] προκύπτει από ανοιχτα διαστήματα της μορφής <math>B_r(p)=\{x\in\R:|x-p|<r\}</math>. |
||
| Γραμμή 136: | Γραμμή 136: | ||
[[sv:Reella tal]] |
[[sv:Reella tal]] |
||
[[th:จำนวนจริง]] |
[[th:จำนวนจริง]] |
||
[[tr: |
[[tr:Reel sayılar]] |
||
[[uk:Дійсні числа]] |
[[uk:Дійсні числа]] |
||
[[uz:Haqiqiy sonlar]] |
[[uz:Haqiqiy sonlar]] |
||
Έκδοση από την 09:39, 28 Ιουνίου 2010
Στα μαθηματικά, οι πραγματικοί αριθμοί γίνονται αντιληπτοί διαισθητικά ως το σύνολο όλων των αριθμών που είναι σε ένα προς ένα αντιστοιχία με τα σημεία μιας άπειρης ευθείας, που καλείται ευθεία των πραγματικών αριθμών ή πραγματικός άξονας. Ο όρος "πραγματικός αριθμός" πλάστηκε εκ των υστέρων σε αντιδιαστολή προς τους "φανταστικούς αριθμούς", των οποίων η ένωση με τους πραγματικούς δίνει τους μιγαδικούς. Οι πραγματικοί αριθμοί είναι το κεντρικό αντικείμενο μελέτης της πραγματικής ανάλυσης. Σε αυστηρή μαθηματική γλώσσα, ο πραγματικός αριθμός ορίζεται ως εξής:
Άν για τον αριθμό L ισχύει , όπου an μια ρητή προσέγγιση του L με n δεκαδικά ψηφία, τότε ο L είναι πραγματικός αριθμός. Αυτό σημαίνει ότι πραγματικός είναι ο αριθμός του οποίου μπορούμε να γράψουμε μια δεκαδική προσέγγιση, όπως στον αριθμό π~3,14.
Οι πραγματικοί αριθμοί διακρίνονται σε ρητούς αριθμούς (που μπορούν να εκφραστούν ως κλάσματα με ακέραιο αριθμητή και παρονομαστή) και σε άρρητους αριθμούς (που δεν μπορούν να εκφραστούν επακριβώς ως κλάσματα). Οι ρητοί μαζί με τους άρρητους αποτελούν ένα συνεχές.
Κάθε "φυσικό μέγεθος" που μπορεί να μετρηθεί εκφράζεται συνήθως με έναν πραγματικό αριθμό. Το σύνολο των πραγματικών αριθμών συμβολίζεται με .
Αξιωματική Θεμελίωση των Πραγματικών Αριθμών
Ονομάζουμε σύνολο των πραγματικών αριθμών ένα σύνολο το οποίο ικανοποιά τα παρακάτω τρία αξιώματα:
- Το σύνολο αποτελεί σώμα. Αναλυτικά:
- Για όλα τα x, y, και z στο , ισχύει x + (y + z) = (x + y) + z and x(yz) = (xy)z.
- Για όλα τα x και y στο , x + y = y + x και xy = yx.
- Για όλα τα x, y, και z στο , ισχύει x(y + z) = (xy) + (xz).
- Για όλα τα x στο , υπάρχει ένα στοιχείο 0, τέτοιο ώστε x + 0 = x = 0 + x και ένα στοιχείο 1 0, τέτοιο ώστε x1 = x = 1x.
- Για όλα τα x στο , υπάρχει ένα στοιχείο −x στο R, τέτοιο ώστε x + (−x) = 0 = (-x) + x.
- Για όλα τα x ≠ 0 στο , υπάρχει ένα στοιχείο x−1 στο R, τέτοιο ώστε xx −1 = 1 = x −1 x.
- Το σώμα είναι διατεταγμένο. Αναλυτικά για x, y, και z στο
- ισχύει ακριβώς μια από τις: x<y, x=y, x>y (τριχοτομία)
- αν x<y τότε x+z<y+z
- αν x>0 και y>0 τότε xy>0.
- Το διατεταγμένο σώμα είναι πλήρες: Κάθε μη κένό άνω φραγμένο υποσύνολό του έχει ένα ελάχιστο άνω φράγμα (suprimum).
- Ισοδύναμα μπορούμε να ορίσουμε την πληρότητα με τον ορισμό στους μετρικούς χώρους, δηλαδή κάθε ακολουθία Κωσύ συγλίνει.
Αποδεικνύεται ότι όλα τα σύνολα που ικανοποιούν τα παραπάνω τρία αξιώματα είναι ισομορφικά, κάτι που μας επιτρέπει να λέμε ότι υπάρχει μόνο ένα πλήρες διατεταγμένο σώμα, το σύνολο των πραγματικών αριθμών. Το σύνολο των ρητών αν και είναι διατεταγμένο σώμα δεν ικανοποιεί την Αρχή της πληρότητας ενώ τα σύνολα των φυσικών και ακεραίων δεν αποτελούν σώματα.
Κατασκευή
Για την κατασκευή των πραγματικών αριθμών χρησιμοποιούμε ως αφετερία το σύνολο των ρητών αριθμών . Ζητούμε ένα σύνολο που είναι διατεταγμένο σώμα όπως το και επιπλέον ικανοποιεί το αξίωμα της πληρότητας. Αυτό μπορεί να γίνει με διάφορες μεθόδους.
- Τομές Dedekind:
Οι τομές Dedekind είναι άνω φραγμένα ανοιχτά υποσύνολα του . Για κάθε ρητό αριθμό θεωρουμε την τομή Dedekind . To κατασκευάζεται από το σύνολο των τομών Dedekind.
- Ακολουθίες Κωσύ
Θεωρούμε τις ακολουθίες Κωσύ στον και ορίζουμε την ακόλουθη σχέση ισοδυναμίας: Δύο ακολουθίες Κωσύ (αν) και (βν) είναι ισοδύναμες ανν η διαφορά τους τείνει στο μηδέν, δηλαδή ανν για κάθε ρητό ε>0 υπάρχει φυσικός Ν, τέτοιος ώστε |αν - βν|<ε για κάθε ν>Ν. To κατασκευάζεται από το σύνολο των κλάσεων ισοδυναμίας.
Η ευθεία των πραγματικών αριθμών
Το σύνολο των πραγματικών αριθμών μπορεί να παρασταθεί σε μια ευθεία, της οποίας κάθε σημείο αντιστοιχεί σε έναν μοναδικό πραγματικό αριθμό. Στην ευθεία αυτή, τα σημεία είναι διατεταγμένα έτσι ώστε κινούμενοι από αριστερά προς τα δεξιά η τιμή των πραγματικών αριθμών να αυξάνεται. Έτσι, επιλέγοντας ένα σημείο x, κάθε σημείο αριστερά από αυτό αντιστοιχεί σε πραγματικό αριθμό μικρότερο από αυτόν που αντιστοιχεί στο x, ενώ κάθε σημείο δεξιά απ'αυτό αντιστοιχεί σε μεγαλύτερο πραγματικό αριθμό. Αν x=0, τότε αριστερά βρίσκονται όλα τα σημεία που αντιστοιχούν στους αρνητικούς πραγματικούς αριθμούς, ενώ δεξιά βρίσκονται τα σημεία που αντιστοιχούν στους θετικούς.
Το σύνολο είναι ολικά διατεταγμένο, δηλαδή αν επιλέξουμε δύο αριθμούς , τότε θα ισχύει μία από τις τρεις παρακάτω σχέσεις:
- .
Στον πραγματικό άξονα, αυτό σημαίνει ότι αν επιλέξουμε δύο σημεία α και β πάνω του, τότε ή το α είναι αριστερά του β ή το α θα συμπέσει με το β ή το α θα είναι δεξιά του β. Η πρόταση αυτή ακούγεται προφανής.
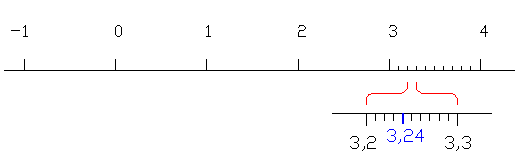
Η ευθεία των πραγματικών αριθμών δεν διακόπτεται και πουθενά δεν έχει κενά. Αντίστοιχα, το σύνολο των πραγματικών αριθμών είναι τόσο πυκνό που πάντα μεταξύ δύο πραγματικών αριθμών, όσο μικρή απόσταση κι αν έχουν μεταξύ τους, θα υπάρχει τουλάχιστον ακόμη ένας.
Πληθάριθμος
Το σύνολο των πραγματικών αριθμών είναι υπεραριθμήσιμο. Σε αντίθεση δηλαδή με τους φυσικούς αριθμούς δεν μπορούμε να απαριθμίσουμε όλους τους πραγματικούς. Ο πληθάριθμος του συμβολίζεται με τον πληθάριθμο του συνεχούς . Σύμφωνα με την υπόθεση του συνεχούς του Καντόρ, ότι δεν υπάρχει σύνολο με πληθάριθμο μεταξύ αυτου των φυσικών και αυτού των πραγματικών αριθμών, ο πληθάριθμος του συνεχούς είναι ίσος με (άλεφ-ένα).
Τοπολογικές ιδιότητες
Το σύνολο των πραγματικών αριθμών μαζί με την ευκλείδεια μετρική αποτελούν μετρικό χώρο. Η συνήθης τοπολογία προκύπτει από ανοιχτα διαστήματα της μορφής .
O δεν είναι συμπαγής μετρικός χώρος. Υπάρχει ανοιχτή κάλυψη του για την οποία δεν υπάρχει πεπερασμένη ανοιχτή υπο-κάλυψη. Π.χ. θεωρούμε τα σύνολα . Η ένωσή τους είναι μια κάλυψη του . Δεν υπάρχει όμως πεπερασμένος αριθμός των που μπορούν να καλυψουν τον . Ο είναι όμως τοπικά συμπαγής, για κάθε πραγματικό αριθμό υπάρχει περιοχή του, της οποίας η κλειστή θήκη είναι συμπαγής.
O είναι συναφής χώρος, αφού δε μπορεί να διαιρεθεί σε δυο ανοιχτά ξένα μεταξύ τους σύνολα.














