Μορφοκλασματικό τοπίο
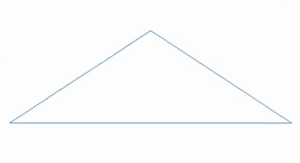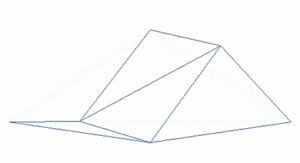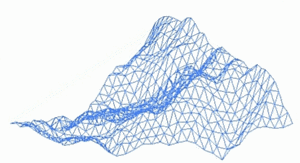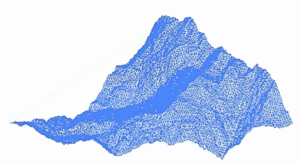
Ένα μορφοκλασματικό τοπίο ή μια μορφοκλασματική επιφάνεια δημιουργείται με τη χρήση ενός στοχαστικού αλγορίθμου που έχει σχεδιαστεί για να παράγει μορφοκλασματική συμπεριφορά που μιμείται την εμφάνιση του φυσικού εδάφους. Με άλλα λόγια, η επιφάνεια που προκύπτει από τη διαδικασία δεν είναι μια προσδιοριζόμενη, αλλά μια τυχαία επιφάνεια που παρουσιάζει φρακταλική συμπεριφορά[1].
Πολλά φυσικά φαινόμενα παρουσιάζουν κάποια μορφή στατιστικής αυτοομοιότητας που μπορεί να μοντελοποιηθεί από φράκταλ επιφάνειες[2]. Επιπλέον, οι μεταβολές στην υφή της επιφάνειας παρέχουν σημαντικές οπτικές ενδείξεις για τον προσανατολισμό και τις κλίσεις των επιφανειών και η χρήση σχεδόν αυτοομοειδών φράκταλ μοτίβων μπορεί να βοηθήσει στη δημιουργία οπτικών εφέ που μοιάζουν φυσικά[3]. Η μοντελοποίηση των τραχειών επιφανειών της Γης μέσω της κλασματικής κίνησης Μπράουν προτάθηκε για πρώτη φορά από τον Μπενουά Μάντελμπροτ[4].
Δεδομένου ότι το επιδιωκόμενο αποτέλεσμα της διαδικασίας είναι η παραγωγή ενός τοπίου και όχι μιας μαθηματικής συνάρτησης, συχνά εφαρμόζονται διαδικασίες σε τέτοια τοπία που μπορεί να επηρεάσουν τη στασιμότητα και ακόμη και τη συνολική φρακταλική συμπεριφορά μιας τέτοιας επιφάνειας, προς το συμφέρον της παραγωγής ενός πιο πειστικού τοπίου.
Σύμφωνα με τον Ρ. Ρ. Σίρερ, η παραγωγή επιφανειών και τοπίων που μοιάζουν με φυσικά τοπία αποτέλεσε ένα σημαντικό σημείο καμπής στην ιστορία της τέχνης, όπου η διάκριση μεταξύ γεωμετρικών, παραγόμενων από υπολογιστή εικόνων και φυσικής, ανθρωπογενούς τέχνης έγινε δυσδιάκριτη[5]. Η πρώτη χρήση ενός τοπίου που δημιουργήθηκε από φράκταλ σε κινηματογραφική ταινία έγινε το 1982 για την ταινία "Σταρ Τρεκ ΙΙ: Η οργή του Καν". Ο Λόρεν Κάρπεντερ τελειοποίησε τις τεχνικές του Μάντελμπροτ για να δημιουργήσει ένα εξωγήινο τοπίο[6].
Συμπεριφορά των φυσικών τοπίων
[Επεξεργασία | επεξεργασία κώδικα]


Το κατά πόσον τα φυσικά τοπία συμπεριφέρονται γενικά με μορφοκλασματικό τρόπο αποτέλεσε αντικείμενο ορισμένων ερευνών. Από τεχνική άποψη, κάθε επιφάνεια στον τρισδιάστατο χώρο έχει τοπολογική διάσταση 2, και επομένως κάθε φρακταλική επιφάνεια στον τρισδιάστατο χώρο έχει διάσταση Χάουσντορφ μεταξύ 2 και 3.[7] Τα πραγματικά τοπία, ωστόσο, έχουν διαφορετική συμπεριφορά σε διαφορετικές κλίμακες. Αυτό σημαίνει ότι μια προσπάθεια υπολογισμού της "συνολικής" διάστασης φράκταλ ενός πραγματικού τοπίου μπορεί να οδηγήσει σε μέτρα αρνητικής διάστασης φράκταλ ή διάστασης φράκταλ πάνω από 3. Ειδικότερα, πολλές μελέτες φυσικών φαινομένων, ακόμη και εκείνων που συνήθως θεωρείται ότι παρουσιάζουν φρακταλική συμπεριφορά, δεν το κάνουν, για περισσότερο από μερικές τάξεις μεγέθους. Παραδείγματος χάριν, η εξέταση της δυτικής ακτογραμμής της Βρετανίας από τον Ρίτσαρντσον έδειξε μορφοκλασματική συμπεριφορά της ακτογραμμής σε δύο μόνο τάξεις μεγέθους[8] . γενικά, δεν υπάρχει λόγος να υποθέσουμε ότι οι γεωλογικές διεργασίες που διαμορφώνουν το έδαφος σε μεγάλες κλίμακες (για παράδειγμα η τεκτονική των πλακών) παρουσιάζουν την ίδια μαθηματική συμπεριφορά με εκείνες που διαμορφώνουν το έδαφος σε μικρότερες κλίμακες (για παράδειγμα, ο ερπυσμός του εδάφους).
Τα πραγματικά τοπία έχουν επίσης διαφορετική στατιστική συμπεριφορά από τόπο σε τόπο, παραδείγματος χάριν οι αμμώδεις παραλίες δεν παρουσιάζουν τις ίδιες ιδιότητες φράκταλ με τις οροσειρές. Μια φράκταλ συνάρτηση, ωστόσο, είναι στατιστικά στάσιμη, που σημαίνει ότι οι βασικές στατιστικές της ιδιότητες είναι οι ίδιες παντού. Έτσι, οποιαδήποτε πραγματική προσέγγιση στη μοντελοποίηση τοπίων απαιτεί τη δυνατότητα διαμόρφωσης της μορφοκλασματικής συμπεριφοράς στο χώρο. Επιπλέον, τα πραγματικά τοπία έχουν πολύ λίγα φυσικά ελάχιστα (τα περισσότερα από αυτά είναι λίμνες), ενώ μια φράκταλ συνάρτηση έχει κατά μέσο όρο τόσα ελάχιστα όσα και μέγιστα. Τα πραγματικά τοπία έχουν επίσης χαρακτηριστικά που προέρχονται από τη ροή του νερού και του πάγου πάνω στην επιφάνειά τους, τα οποία τα απλά φράκταλ δεν μπορούν να διαμορφωθούν[9].
Εξαιτίας αυτών των εκτιμήσεων οι απλές φράκταλ συναρτήσεις είναι συχνά ακατάλληλες για τη μοντελοποίηση τοπίων. Οι πιο εξελιγμένες τεχνικές (γνωστές ως "τεχνικές πολλαπλών fractal") χρησιμοποιούν διαφορετικές διαστάσεις φράκταλ για διαφορετικές κλίμακες και έτσι μπορούν να μοντελοποιήσουν καλύτερα τη συμπεριφορά του φάσματος συχνοτήτων των πραγματικών τοπίων[10].
Δημιουργία μορφοκλασματικών τοπίων
[Επεξεργασία | επεξεργασία κώδικα]Ένας τρόπος για να δημιουργήσετε ένα τέτοιο τοπίο είναι να χρησιμοποιήσετε τον αλγόριθμο τυχαίας μετατόπισης του μέσου σημείου, στον οποίο ένα τετράγωνο υποδιαιρείται σε τέσσερα μικρότερα ίσα τετράγωνα και το κεντρικό σημείο μετατοπίζεται κάθετα κατά κάποιο τυχαίο ποσό. Η διαδικασία επαναλαμβάνεται στα τέσσερα νέα τετράγωνα, και ούτω καθεξής, μέχρι να επιτευχθεί το επιθυμητό επίπεδο λεπτομέρειας. Υπάρχουν πολλές διαδικασίες φράκταλ (όπως ο συνδυασμός πολλαπλών οκτάβων θορύβου τύπου Simplex) ικανές να δημιουργήσουν δεδομένα εδάφους, ωστόσο ο όρος "φράκταλ τοπίο" έχει γίνει πιο γενικός με την πάροδο του χρόνου.
Φράκταλ φυτά
[Επεξεργασία | επεξεργασία κώδικα]Τα φράκταλ φυτά μπορούν να δημιουργηθούν με τη βοήθεια διαδικαστικών συστημάτων L σε σκηνές που δημιουργούνται από υπολογιστή[11].
Δείτε επίσης
[Επεξεργασία | επεξεργασία κώδικα]- Αλγόριθμος διαμαντιού τετραγώνου
- Καμπύλη που γεμίζει το χώρο
- Νιφάδα του Κοχ
- Καμπύλη Χίλμπερτ
- Καμπύλη του δράκου
- Σπόγγος του Μένγκερ
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ «The Fractal Geometry of Nature».
- ↑ Advances in multimedia modeling: 13th International Multimedia Modeling by Tat-Jen Cham 2007 (ISBN 3-540-69428-5) page [1]
- ↑ Human symmetry perception and its computational analysis by Christopher W. Tyler 2002 (ISBN 0-8058-4395-7) pages 173–177 [2]
- ↑ Dynamics of Fractal Surfaces by Fereydoon Family and Tamas Vicsek 1991 (ISBN 981-02-0720-4) page 45 [3]
- ↑ Rhonda Roland Shearer "Rethinking Images and Metaphors" in The languages of the brain by Albert M. Galaburda 2002 (ISBN 0-674-00772-7) pages 351–359 [4]
- ↑ Briggs, John (1992). Fractals: The Patterns of Chaos : a New Aesthetic of Art, Science, and Nature. Simon and Schuster. σελ. 84. ISBN 978-0671742171. Ανακτήθηκε στις 15 Ιουνίου 2014.
- ↑ *Lewis, J.P. «Is the Fractal Model Appropriate for Terrain?» (PDF).
- ↑ *Richardson, L.F. (1961). «The Problem of Continuity». General Systems Yearbook. 6: 139–187.
- ↑ *Musgrave, Ken (1993). «Methods for Realistic Landscape Imaging» (PDF).
- ↑ *van Lawick van Pabst, Joost· Jense, Hans (2001). «Dynamic Terrain Generation Based on Multifractal Techniques» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 24 Ιουλίου 2011.
- ↑ de la Re, Armando· Abad, Francisco· Camahort, Emilio· Juan, M. C. (2009). «Tools for Procedural Generation of Plants in Virtual Scenes» (PDF). Computational Science – ICCS 2009. Lecture Notes in Computer Science. 5545. σελίδες 801–810. doi:10.1007/978-3-642-01973-9_89. ISBN 978-3-642-01972-2.
